Quantitative determination of the critical points of Mott metal–insulator transition in strongly correlated systems

Yuekun Niu(牛月坤), Yu Ni(倪煜), Jianli Wang(王建利), Leiming Chen(陳雷鳴),Ye Xing(邢曄), Yun Song(宋筠), and Shiping Feng(馮世平)

1School of Physical Science and Technology,Inner Mongolia University,Hohhot 010021,China

2College of Physics and Electronic Information,Yunnan Normal University,Kunming 650500,China

3School of Materials Science and Physics,China University of Mining and Technology,Xuzhou 221116,China

4Department of Physics,Beijing Normal University,Beijing 100875,China

Keywords: critical point, metal–insulator transition, local quantum state fidelity, strongly correlated system,quasiparticle coherent weight

1.Introduction

The Mott metal–insulator transition(MIT),[1–3]resulting from the interplay between the kinetic energytand the on-site Coulomb repulsive interactionUamong electrons,represents a fundamental manifestation of strong electron correlation effects.Experimental investigations have demonstrated the presence of the unconventional superconductivity and other exotic quantum phenomena in the metallic phase close to the Mott MIT.[3]This is why the quantitative determination of the critical point of the Mott MIT is crucial to deeply understanding the essential physics of these novel quantum phenomena in strongly correlated systems.

Although enormous efforts have been made at the experimental and theoretical levels to understand the physical origin of the Mott MIT,together with the associated novel quantum phenomena,[3]the quantitative determination of the critical point of the Mott MIT is still a challenging issue.In early studies,it was shown in the Gutzwiller approximation that the quasiparticle coherent weight can be used as a physical quantity to determine the critical point of the Mott MIT, where the quasiparticle coherent weightZFdisappears and the effective mass diverges as 1/ZFwhen the strength of the Coulomb interaction approaches its critical value.[4–6]The quasiparticle coherent peak around the Fermi surface comes mainly from the scattering of electrons on the local-spin fluctuations.Hence,its disappearance at the critical point of MIT can also be tracked by analyzing the energy dependence of the electron self-energy with different Coulomb repulsive interactions.[7]Later, a systematic analysis[8]based on the dynamical meanfield theory (DMFT) indicated that at low-temperature, the opening of the gap and the vanishing of the quasiparticle coherent peak do not happen at the same critical value ofUc.Instead, MIT is found as a function ofU/t, with the corresponding metallic and insulating solutions coexisting betweenUc2andUc1, respectively.Since then, a series of studies focusing on the region of the metallic and insulating solutions coexisting betweenUc2andUc1has been made.[9–15]In practice, these studies also indicate that the quasiparticle coherent weightZFmay not be able to mark out these two distinct forms of the critical points in the MIT due to the coexistence of a branch of metastable metallic solution that connects the two stable metallic and insulating solutions ofZF.[16,17]In this case,a natural question is raised: is there a more proper physical quantity to present the existence of the two distinct forms of the critical points in the Mott MIT?

In this paper, we study the one-band Hubbard model by using the DMFT with the Lanczos method as its impurity solver.It is confirmed that the local quantum state fidelity(LQSF), as a proper physical quantity, can provide a convenient way to identify the critical point of the Mott MIT.In particular,it can give a consistent description of the two different forms of the critical points in the Mott MIT.

2.Models and methods

The one-band Hubbard model is the simplest model that captures the essential physics of MIT in a strongly correlated system.The Hamiltonian of the one-band Hubbard model is given by[18–21]

where the summation〈ij〉is over all sitesi, and for each sitei,restricted to its nearest-neighbor(NN)sitesj,tdenotes the electron NN hopping amplitude,Uis the on-site Coulomb repulsion between electrons,andμis the chemical potential.(diσ)is the creation(annihilation)operator for an electron with spinσat lattice sitei,andniσis the occupation number operator of electrons at lattice sitei.Unless explicitly stated,we sett=1 as the energy scale in this paper.The electron Green’s function of the Hubbard model(1)can be expressed formally as

where the energy dispersion in the tight-binding approximation can be obtained directly bywhile the effect of interaction in the Hubbard model (1) has been encoded in the electron self-energyΣσ(k,ω).It should be emphasized that in the infinite-dimensional system, this electron self-energyΣσ(k,ω) is momentum independent.The DMFT[22,23]provides an approximate solution to this electron self-energyΣσ(k,ω)in a finite-dimensional system by setting, where the momentum independence of the electron self-energycan be obtained in terms of an auxiliary impurity model consisting of a single interacting site in a self-consistently determined bath.[15]In other words,the auxiliary impurity model provides a way to calculate the local electron self-energyand to use the entire repertoire of the electron Green’s function with the contribution to the electron self-energy taken from the auxiliary impurity system rather than from a perturbation expansion.[24]

We evaluate the electron self-energy of the Hubbard model (1) by using the DMFT with the Lanczos method as its impurity solver.In the framework of the DMFT,the Hubbard model (1) is mapped onto an effective single impurity model by dropping the nonlocal contribution to the electron self-energy,

which becomes exact in the limit of the infinite lattice coordination.[25]Here,d?σ(dσ) creates (annihilates) a particle in the impurity orbital and(cmσ) creates (annihilates) an electron in a conduction band, where the impurity orbital and conduction band are coupled with each other via effective parametersεmandVm, which are determined by the self-consistent DMFT calculation utilizing an impurity solver.In the following discussions, we introduce the local-electron Green’s function in real-space as[26,27]

with the imaginary timeτ= it.This local-electron Green’s function (4) in energy space can be obtained directly by performing the Fourier transformation

where?β ≤τ ≤βand the fermionic Matsubara frequencyωn=(2n+1)π/βwithn=0,±1,±2,....

The local properties of the Hubbard model on the Bethe lattice can be obtained via a single-site impurity problem supplemented by the following self-consistent relation:[28,29]

whereG0σis the bare Green’s function.The self-consistent relation ensures that the on-site (local) component of the Green’s functioncoincides with the Green’s functionGσ(iωn)calculated from the effective action.

The Green’s functionGimp(iωn)of the impurity model(3)is then calculated by the Lanczos method,[30–32]which can be expressed explicitly as[8,28,33]

withG+σ(iωn)andG?σ(iωn)given by

wherean(bn) is thenth sub-diagonal element of the tridiagonalized Hamiltonian obtained by the Lanczos method and|φ0〉 is the ground state of the Hamiltonian (3).In our calculations, we choosenb=7 andβ=1024 to assure the accuracy of the self-consistency calculations, especially in the low-energy region.It is worth noting thatβplays a role of frequency cutoff,[28]and hence 1/βcan be regarded as a fictitious temperature.In this work,we restrict our calculations to zero-temperature conditions.

The Green’s function behaves differently depending on whether the eigenstates are localized or extended,[34]which helps us to obtain the interaction effect on the phase transitions.For an interaction-driven Mott transition, the ground state of the metallic phase is gapless, while the Mott insulating ground state has a gap.As discussed in Refs.[35–38],there is a short-range entanglement in gapped quantum states,which corresponds to a symmetry-protected topological(SPT)order.[37]We extend the classification method of the SPT phases in higher dimensions to label-gapped quantum phases based on the four occupation states of electrons on an impurity site.Additionally, the fidelity per site method[39,40]is in accord with the DMFT idea of mapping a lattice model onto an effective single-site impurity model.[8]It has been demonstrated that the fidelity per site method can help us understand how quantum phase transitions are influenced by quantum fluctuations.[39,40]Considering the scenario of the SPT[35–38,41,42]and the sensitive feature of fidelity in detecting quantum fluctuation,[40]we introduce the local quantum state fidelity[43]of single impurity site as

with

Here, ?Pis the net spin projection operator for impurity site with〈0|?P|0〉=〈↑↓|?P|↑↓〉=0,〈↑|?P|↑〉=1,and〈↓|?P|↓〉=represents the ground state wave function of the single impurity site with an interaction strength ofU(U+0+).The factor eiωn0+is introduced to ensure the convergence of the summations.

In the metallic phase,the average spin of the DMFT impurity〈σ〉tis zero[44]because of the high symmetry of the spin at the impurity site obtained by Landau’s theory.The probabilities of doublon and holon[45]occurrence are equal, i.e.,p21=p24,and the probabilities of spin-up and spin-down states havep22=p23,and therefore the LQSF remains zero(Lo=0).However, the insulating ground state of the DMFT impurity model is double-degenerate with singly occupied states of opposite spins (|↑〉 or|↓〉), and thusLohas two solutions asLo=±C, whereCis a finite positive constant.Because both the positive and negative signs ofLoindicate the same insulating phase, we only show the absolute value ofLoin the figures.As a result, a sudden rise of the LQSF at the critical interactionUcwill be found(note thatLo=±Cdoes not mean that the system is antiferromagnetic or ferromagnetic).Specifically,the local moment of the impurity site is zero due to the double degeneration of the ground state.Therefore, the Mott MIT can be depicted by the LQSF.It is worth noticing that the behavior ofLois the same as the topological invariant found in Ref.[46].

To evaluate the frequency summation over the Matsubara Green’s function, we need to further simplify the above formula by considering the interacting Matsubara Green’s function at the poles,which holds

With the help of the above Eq.(12), the LQSF of the impurity site can be rewritten explicitly asLo=indicating thatLocan be directly obtained by a summation of the positive frequencies in the effective on-site problem.

3.Results

We define the quasiparticle coherent weightZFas[27,47]

where the local self-energyΣσ(iωn) is obtained from the local Green’s function in Eq.(7).In the following discussions,we study the Mott MIT of the Hubbard model at half-filling in terms of the evolution of the LQSFLoat the impurity site with the on-site Coulomb repulsive interactionU.In Fig.1 we plot 2Loas a function of interactionU,where the red dashedline indicates the position of the critical point of the Mott MIT.For a better comparison,the evolution of the quasiparticle coherent weightZF(blue solid-line)withUis also presented in Fig.1.ZFusually decreases with increasingUand keeps very close to zero when approaching the critical interactionUcof the Mott MIT,near which the systematic errors ofZFincrease significantly, leading to difficulties in the quantitative determination of the critical point of MIT.More crucially, within the framework of DMFT, two metallic results with different slope dZF/dUare found to coexist in a finite range of interaction strengths,[16,17]and thus comparing the respective energies with the energy of the insulator is suggested.[17]Consequently,it becomes quite difficult and inconvenient to numerically determine the actual critical interactionUcby the quasiparticle coherent weight.In a striking contrast to the complex ofZFthat has two metallic solutions in the coexistence region of interactionU, the LQSFLokeeps equal to zero for both the metastable and stable metallic solutions whenU ＜Uc, as shown in Fig.1.

Fig.1.The local quantum state fidelity Lo (red dotted line)as a function of interaction U.The Mott metal–insulator transition occurs at a critical value of Uc=6.5.For comparison,the evolution of the quasiparticle coherent weight ZF with U (blue solid line)is also presented.In the numerical calculations we chose nb=7 and β =1024.

However,at the critical pointUc=6.5 of MIT,the LQSF jumps abruptly fromLo=0 in the metallic phase to 2Lo≈1.0 in the insulating phase.Our results indicate clearly that the LQSFLoat the impurity site is very sensitive to the existence of the resonant peak at the Fermi level, which therefore is a more proper physical quantity to quantitatively depict the critical point of the Mott MIT.

As to the two classes of solutions, (i) the solution from the metallic phase towards the critical interaction of MIT(the metallic-phase solutionUc2) and (ii) the solution from the insulating phase towards the critical point of MIT (the insulating-phase solutionUc1),the LQSFLoas a more proper physical quantity of MIT can give a natural explanation of the difference between the metallic and insulating solutions.In this case, we have made a series of calculations for 2Lo, and the results of the metallic solution of 2Lo(red dotted line)and the insulating solution (blue solid line) are plotted in Fig.2,whereUc1=4.7 andUc2=6.5 are the critical points of the insulator-to-metal transition and the metal-to-insulator transition, respectively.Our findings of the critical interactions are in agreement with the DMFT results from the numerical renormalization group solver[5]Uc1=5.0 andUc2=5.88,and the dynamical density renormalization group method[48]Uc1=4,76 andUc2=6.14.The results in Fig.2 show that apart from a metallic phase in the weak interaction region(U ＜Uc1) and an insulating phase in the strong interaction region (U ＞Uc2), there is an intermediate interaction region(Uc1＜U ＜Uc2), where the metallic solution coexists with the insulating solution.Within this intermediate interaction region, 2Loas a function ofUexhibits a hysteretic behavior since both the metallic and insulating solutions are found to be attractive points of a particle–hole symmetry system.[15]The results in Figs.1 and 2 therefore show thatLois a more proper physical parameter to give a quantitative description of the Mott MIT in a strong correlation system.

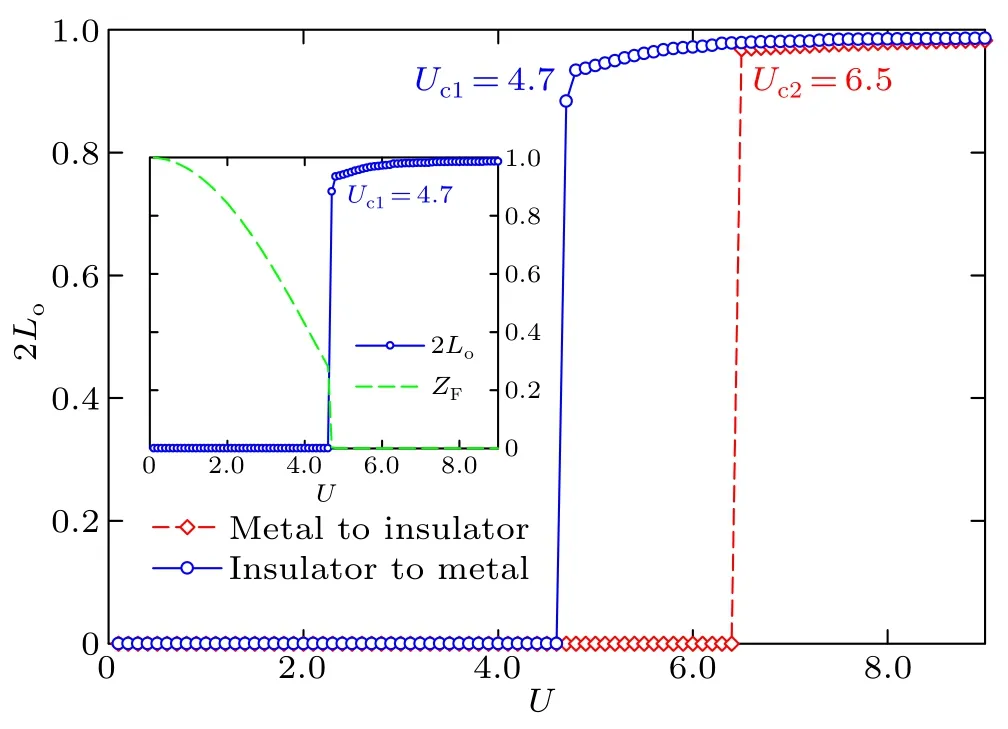
Fig.2.The local quantum state fidelity Lo as a function of interaction U.The blue line indicates the critical point at Uc1 =4.7, while the red line denotes the critical point at Uc2 =6.5.Within the region between the two critical points of Uc1 and Uc2,the insulating solution(blue solid line)and metallic solution(red dotted line)coexist.Inset:the comparison of the local quantum state fidelity (blue solid line) and the quasiparticle coherent weight(green dotted line)for the insulating-phase solution.

Although the summation of Matsubara frequency is from zero to infinity,the actual calculation is performed numerically with the infinitude of Matsubara frequencyn=0,1,2,...,∞→n= 0,1,2,...,nmaxreplaced by a finitenmax.In this case,we have made a series of calculations for 2Loas a function ofUat different cutoffnmax, and the results are plotted in Fig.3,where the critical points atnmax=2048,nmax=8192,nmax=32768 andnmax=65536 are very close to each other,indicating that for the large enoughnmax, the error bars are small enough.In particular,Uccan be extrapolated asUc=6.5 in the case ofnmax=∞.

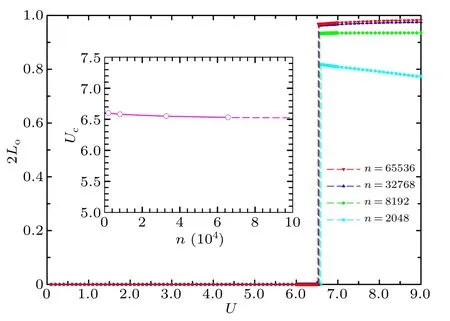
Fig.3.The local quantum state fidelity Lo as a function of the interaction U for various cutoff values n in the series summation.The evolution of Uc with n (circles) is presented (inset) along with the fitting line (solid line)and its extension(dashed line).

The Hilbert space of each site in the Hubbard model (1)consists of four states,|0〉,|↑〉,|↓〉,|↑↓〉,corresponding to the zero,spin-up,spin-down and double-electron-occupied states,respectively.The probabilities of the zero,spin-up,spin-down and double-occupied states at the single impurity site of the metallic solution are plotted in Fig.4, which shows clearly that the probabilities of the zero and double-occupied states are equal and decrease simultaneously in the metallic phase.However, the probability of the spin-up singly occupied state increases with the increase of the on-site Coulomb interactionUand jumps top2≈1 at the critical pointUc2=6.5.The same feature for the probability of the spin-down singly occupied state is found in the insulating phase due to the degeneration (see Fig.4 inset).Concomitantly, the LQSF is equal to zero when the probability of the spin-up singly occupied state is equal to that of the spin-down singly occupied state in the metallic phase.However, in a striking contrast to the case in the metallic phase,the feature of the probability of the spin-up singly occupied state is quite different from that of the probability of the spin-down singly occupied state in the insulating phase, and a jump of the LQSF is found at the critical point due to the presence of two degenerate solutions with opposite spin occupancies.The above results correspond to the theoretical prediction of Eq.(11).This is why the LQSF in Eq.(11)is a more proper physical quantity to give a quantitative depiction of two distinct forms of the critical points in the MIT of a strongly correlated system.

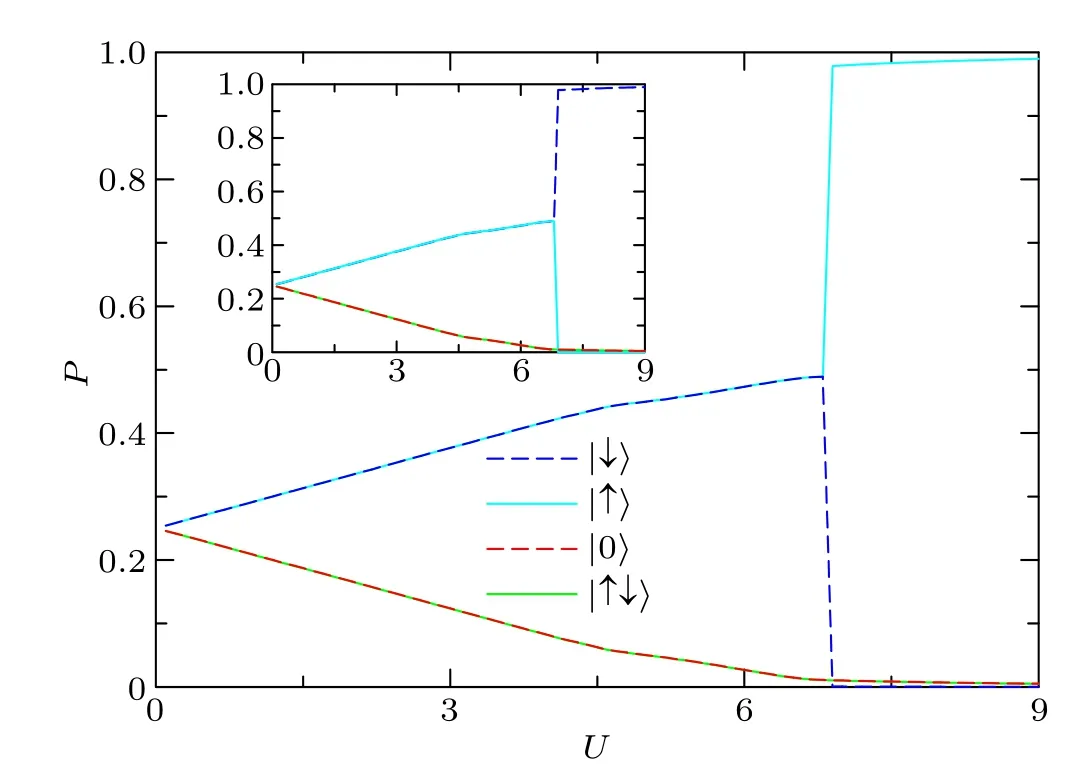
Fig.4.The probabilities p2 of the zero-occupied state |0〉 (red dashed line), spin-up occupied state |↑〉 (cyan solid line), spin-down occupied state|↓〉(blue dashed line)and double-occupied state|↑↓〉(green solid line)in the impurity ground state as a function of the interaction U.Inset:another solution with opposite p2 of the spin-up and spin-down occupied states whenU ＞Uc,demonstrating the double-degeneration of the ground state within the insulating phase.

4.Conclusions

Based on the one-band Hubbard model, we have studied the Mott MIT in a strongly correlated system by using the combined approach of the DMFT and the Lanczos technique.Our results clearly demonstrate that the LQSF serves as a proper physical quantity for depicting the Mott MIT in a strongly correlated system.It allows for quantitative determination of the critical points and provides a consistent description of two distinct forms of the critical points.The LQSF can be also used to discuss the novel physics in orbital-selective Mott insulators[49]and superconductors.[50,51]In particular,it may be applied to explain the hysteresis observed experimentally in Mott-field effect transistors.[52]These related works are currently under study.

Acknowledgments

The authors would like to thank Gabriele Bellomia for fruitful discussions.YN is also grateful to Louk Rademaker and Haiming Dong for helpful discussions.Project supported by the Scientific Research Foundation for Youth Academic Talent of Inner Mongolia University(Grant No.10000-23112101/010) and the Fundamental Research Funds for the Central Universities of China (Grant No.JN200208).YS is supported by the National Natural Science Foundation of China(Grant No.11474023).SF is supported by the National Key Research and Development Program of China (Grant No.2021YFA1401803) and the National Natural Science Foundation of China(Grant Nos.11974051 and 11734002).