受疾病意識(shí)影響的時(shí)滯傳染病模型的動(dòng)力學(xué)分析*

郭紅利,謝景力,張美楊

(吉首大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,湖南 吉首 416000)

現(xiàn)實(shí)中,易感者與感染者接觸后,易感者往往不會(huì)馬上顯示出染病特征,而是經(jīng)過(guò)一段時(shí)間才發(fā)病成為感染者.待發(fā)病期間的易感者稱為潛伏者,發(fā)病延遲的這段時(shí)間用時(shí)滯來(lái)表示.受文獻(xiàn)[17]的啟發(fā),筆者擬將易感人群細(xì)分為無(wú)疾病意識(shí)類和有疾病意識(shí)類,并引入潛伏期時(shí)滯,討論一類受疾病意識(shí)影響和時(shí)滯影響的SEIM傳染病模型.

1 模型的建立

將某一研究區(qū)域t時(shí)刻的總?cè)丝跀?shù)N(t)分為4個(gè)不同的類別,即無(wú)疾病意識(shí)易感者Su(t)、有疾病意識(shí)易感者Sa(t)、潛伏者E(t)和感染者I(t),用M(t)表示媒體報(bào)道的疾病信息量.SEIM傳染病模型如下:

(1)

4類倉(cāng)室之間的轉(zhuǎn)換關(guān)系見圖1.

圖1 模型(1)倉(cāng)室及其轉(zhuǎn)換Fig. 1 Compartment and Its Conversion Diagram of Model (1)

假設(shè)模型(1)滿足以下初始條件:

Su(θ)=Φ1(θ),Sa(θ)=Φ2(θ),E(θ)=Φ3(θ),I(θ)=Φ4(θ),M(θ)=Φ5(θ)θ∈[-τ,0],

其中

(2)

設(shè)(Su(t),Sa(t),E(t),I(t),M(t))為模型(1)滿足初值條件(2)的解,顯然對(duì)于?t≥0,有

Su(t)≥0,Sa(t)≥0,E(t)≥0,I(t)≥0,M(t)≥0.

2 平衡點(diǎn)和基本再生數(shù)

(3)

(4)

(5)

(6)

將(3)～(6)式代入模型(1)的第2個(gè)方程,得到關(guān)于I*的三次方程

f(I*)=a3I*3+a2I*2+a1I*+a0.

(7)

其中:

這里:

g(I*)=m3I*3+m2I*2+m1I*+m0.

根據(jù)笛卡爾符號(hào)法則,模型(1)正實(shí)根可能的數(shù)量見表1.

由表1可知:

3 平衡點(diǎn)穩(wěn)定性分析

3.1 無(wú)病平衡點(diǎn)的穩(wěn)定性

模型 (1) 在P0處的Jacobian矩陣

其特征方程為

(8)

顯然,方程(8)恒有3個(gè)負(fù)實(shí)根:λ1=-d,λ2=-δ-d,λ3=-ρ0.方程(8)的其他根由以下方程決定:

(9)

化簡(jiǎn)方程(9),可得

(10)

當(dāng)τ=0時(shí),方程(10)化簡(jiǎn)為

λ2+(η+2d+ω+γ)λ+(η+d)(d+ω+γ)(1-R0)=0.

由Routh Hurwitz判據(jù)可知:當(dāng)R0<1時(shí),P0是局部漸近穩(wěn)定的;當(dāng)R0>1時(shí),P0是不穩(wěn)定的.

當(dāng)τ>0時(shí),設(shè)λ=νi(ν>0)是方程(10)的一個(gè)解.將λ=νi(ν>0)代入方程(10),分離實(shí)部和虛部:

(11)

(12)

將 (11)和(12)式分別平方再相加,可得

ν4+f1ν2+f2=0,

其中f1=d2-η2+(d+ω+γ)2,f2=(d+ω+γ)2(d2-η2+(η+d)R0(2η-(d+η)R0)).令X=ν2,則有

X2+f1X+f2=0.

(13)

接下來(lái)分析τ>0時(shí),方程(13)的根的存在性:

(ⅰ) 當(dāng)f1>0,f2>0時(shí),方程(13)無(wú)正實(shí)根,即對(duì)于?τ>0,無(wú)病平衡點(diǎn)P0是局部漸近穩(wěn)定的.

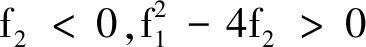
由方程(13),可得相應(yīng)的τn,

(ⅲ) 和 (ⅳ) 對(duì)應(yīng)的τn為

進(jìn)一步可得

由(10),(11)和(12)式,可得

綜上,可得以下結(jié)果:

定理2對(duì)于模型(1) :

(1)當(dāng)τ=0,R0<1時(shí),P0是局部漸近穩(wěn)定的;當(dāng)R0>1時(shí),P0不穩(wěn)定.

(2)當(dāng)R0<1,符合情況(ⅰ)時(shí),對(duì)于?τ>0,無(wú)病平衡點(diǎn)P0是局部漸近穩(wěn)定的.

以上是無(wú)病平衡點(diǎn)P0的局部穩(wěn)定性分析,接下來(lái)分析P0的全局穩(wěn)定性.

定理3當(dāng)R0<1時(shí),對(duì)于?τ≥0,無(wú)病平衡點(diǎn)P0是全局漸近穩(wěn)定的.

定義Lyapunov泛函V=V1+V2,通過(guò)計(jì)算可得,

3.2 地方病平衡點(diǎn)的局部穩(wěn)定性分析

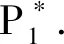
(14)

其中:

Z(t)=(Su(t),Sa(t),E(t),I(t),M(t))T.

這里:

系統(tǒng)(14)對(duì)應(yīng)的特征方程為|λI5×5-(Z1(t)+Z2(t-τ)e-λτ)|=0,這里I5×5是5階單位矩陣.于是

從而

P(λ)+Q(λ)e-λτ=0,

(15)

其中

P(λ)=λ5+B8λ4+B9λ3+B10λ2+B11λ+B12,

Q(λ)=ηλ4+η(B2-A6)λ3+η(B3+B6-ρ0A6)λ2+η(ρA2I*(β1-β2)+B4+

B7+ρ0B6)λ+η(ρA2I*B1+B5+ρ0B7).

這里:

B1=A1β2+A3β2-β1δ-β1A4;

B2=ρ0-A1-A2-A7;

B3=A1A4-A3δ-(ρ0-A7)(A1+A4)-ρ0A7;

B4=ρ0A7(A1+A4)+(ρ0-A7)(A1A4-A3δ);

B5=-ρ0A7(A1A4-A3δ);

B8=ρ0+d-A7-A1-A4;

B9=A1A4-A3δ-(ρ0-A7+d)(A1+A4)+d(ρ0-A7)-ρ0A7;

B10=(ρ0-A7+d)(A1A4-A3δ)-(d(ρ0-A7)-ρ0A7)(A1+A4-ρ0A7d);

B11=(d(ρ0-A7)-ρ0A7)(A1A4-A3δ)+ρ0A7d(A1+A4);

B12=-ρ0A7d(A1A4-A3δ).

當(dāng)τ=0時(shí),P(λ)+Q(λ)=0,于是

P(λ)+Q(λ)=λ5+C1λ4+C2λ3+C3λ2+C4λ+C5.

(16)

其中:

C1=B8+η;C2=B9+η(B2-A6);C3=η(B3+B6-ρ0A6)+B10;

C4=η(ρA2I*(β1-β2)+B4+B7+ρ0B6)+B11;

C5=B12+η(ρA2I*B1+B5+ρ0B7).

根據(jù)Routh Hurwitz判據(jù)可知,方程(16)全部特征根的實(shí)部均為負(fù)數(shù)的充要條件是

于是可得以下結(jié)果:

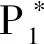
下面討論當(dāng)τ>0時(shí),地方病平衡點(diǎn)的穩(wěn)定情況.當(dāng)τ>0時(shí),假設(shè)λ=νi(ν>0)是(15)式的一個(gè)解.為了方便計(jì)算,令

Q(λ)=ηλ4+D1λ3+D2λ2+D3λ+D4.

其中:

D1=η(B2-A6);D2=η(B3+B6-ρ0A6);D3=η(ρA2I*(β1-β2)+B4+B7+ρ0B6);

D4=η(ρA2I*B1+B5+ρ0B7).

將λ=νi(ν>0)代入(15)式,分離實(shí)部和虛部:

(ην4-D2ν2+D4)cosντ+(D3ν-D1ν3)sinντ=B10ν2-B8ν4-B12,

(17)

(D3ν-D1ν3)cosντ-(ην4-D2ν2+D4)sinντ=-ν5+B9ν3-B11ν.

(18)

將 (17)和(18)式分別平方再相加,可得

ν10+E1ν8+E2ν6+E3ν4+E4ν2+E5=0.

令Y=ν2,則有

Y5+E1Y4+E2Y3+E3Y2+E4Y+E5=0.

(19)

其中:

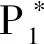
4 數(shù)值模擬

為了研究潛伏時(shí)滯和疾病意識(shí)對(duì)模型(1)的影響,接下來(lái)進(jìn)行數(shù)值模擬.取初始值(Su,Sa,E,I,M)=(9.80,6.65,3.65,4.36,1.28),參數(shù)Λ=0.25,β1=0.045,β2=0.007,α=0.214,K=2,δ=0.075,d=0.025,ω=0.22,γ=0.62,η=0.56,ρ=0.08,ρ0=0.04,計(jì)算得到R0=0.498<1,τ0=6.166 7.

圖2 τ=5.166 7時(shí)P0局部漸近穩(wěn)定Fig. 2 Local Asymptotical Stability of P0 When τ=5.166 7

圖3 τ=5.166 7時(shí)模型(1)出現(xiàn)Hopf分支Fig. 3 Occurrence Hopf Bifurcation in Model (1) When τ=5.166 7

當(dāng)R0<1時(shí),取τ=5.166 7,6.266 7,無(wú)病平衡點(diǎn)P0是全局漸近穩(wěn)定的,符合定理3 (圖4和圖5).

圖4 τ=5.166 7時(shí)P0的相位圖Fig. 4 Phase Diagram of Global Asymptotically Stable P0 When τ=5.166 7

圖5 τ=6.266 7時(shí)P0的相位圖Fig. 5 Phase Diagram of Global Asymptotically Stable P0 When τ=6.266 7

圖6 (7)式的解唯一存在Fig. 6 Uniqueness Solution of Equation (7)

由于模型(1)地方病平衡點(diǎn)的存在情況較復(fù)雜,因此考慮借助Matlab軟件計(jì)算方程(7)的解.取參數(shù)Λ=1,β1=0.15,β2=0.025,α=0.22,K=2,δ=0.075,d=0.025,ω=0.22,γ=0.62,η=0.56,ρ=0.243,ρ0=0.085,計(jì)算可得I*=2.063 5,且唯一存在,滿足定理1的情況(1),如圖6所示.此時(shí),存在地方病平衡點(diǎn)P*(3.910 9,12.679 5,3.187 4,2.063 5,5.899 2),進(jìn)一步計(jì)算得到R0=6.64>1,τ0=11.581 7.

取初始值(Su,Sa,E,I,M)=(3.027 4,15.650 2,2.458 7,1.652 5,4.690 1).當(dāng)τ=10.517 5<τ0時(shí),地方病平衡點(diǎn)P*是局部漸近穩(wěn)定的,最終趨于一個(gè)穩(wěn)定解(圖7和圖8);當(dāng)τ=τ0時(shí),系統(tǒng)發(fā)生Hopf分支,模型(1)出現(xiàn)周期解(圖9和圖10).

為了討論疾病意識(shí)影響因子α和δ的變化對(duì)疾病感染者數(shù)量的影響,固定時(shí)滯τ=8.017 5,分別繪制以α和δ為變化參數(shù)的I(t)的解曲線(圖11和圖12).

圖7 τ=10.517 5時(shí)Su (t),Sa (t),E(t),I(t)的解曲線Fig. 7 Solution Curves of Su (t),Sa (t),E(t),I(t) When τ=10.517 5

圖8 τ=10.517 5時(shí)P*局部漸近穩(wěn)定Fig. 8 Local Asymptotical Stablity of P* When τ=10.517 5

圖10 τ=11.581 7時(shí)模型(1)出現(xiàn)Hopf分支Fig. 10 Occurrence Hopf Bifurcation in Model (1) When τ=11.581 7

圖11 參數(shù)α對(duì)I(t)的影響Fig. 11 Influence of Parameter α on I(t)

圖12 參數(shù)δ對(duì)I(t)的影響Fig. 12 Influence of Parameter δ on I(t)

由圖11可見,α越大,即無(wú)疾病意識(shí)易感者Su(t)轉(zhuǎn)化成有疾病意識(shí)易感者Sa(t)的比例越大,有疾病意識(shí)的人群就越多,疾病的有效傳播率就越低,那么感染者I(t)數(shù)量就越少且越易達(dá)到穩(wěn)定.

由圖12可見,δ越大,即有疾病意識(shí)易感者Sa(t)轉(zhuǎn)化成無(wú)疾病意識(shí)易感者Su(t)的比例越大,無(wú)疾病意識(shí)的人群就越多,疾病的有效傳播率就越高,那么感染者I(t)數(shù)量就越多且越難達(dá)到穩(wěn)定.

5 結(jié)論

為了研究媒體報(bào)道產(chǎn)生的疾病意識(shí)對(duì)傳染病傳播的影響,建立了一類受疾病意識(shí)影響且潛伏期具有時(shí)滯的SEIM傳染病模型,并分析了模型的無(wú)病平衡點(diǎn)和地方病平衡點(diǎn)的存在性和穩(wěn)定性,討論了Hopf分支存在的條件.理論分析和模擬結(jié)果表明:

(1)當(dāng)R0<1時(shí),對(duì)于?τ≥0,無(wú)病平衡點(diǎn)P0是全局漸近穩(wěn)定的.當(dāng)R0>1時(shí),地方病平衡點(diǎn)P*在τ∈[0,τ0)處是局部漸近穩(wěn)定的;在τ=τ0處,模型(1)在P*處出現(xiàn)Hopf分支;在τ>τ0處,P*是不穩(wěn)定的.

(2)個(gè)體疾病關(guān)注意識(shí)越強(qiáng)且越不容易消退,感染者I(t)數(shù)量就越容易得到控制.因此,加大媒體報(bào)道力度,有助于易感人群增強(qiáng)疾病意識(shí),做好個(gè)體保護(hù),減少疾病傳播,從而控制疾病蔓延.