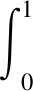Caputo-Fabrizio型分數(shù)階微分方程兩點邊值問題正解的存在性*

王蘭芳

(吉首大學數(shù)學與統(tǒng)計學院,湖南 吉首 416000)

1 問題的提出

分數(shù)階導數(shù)及分數(shù)階微分方程被廣泛應用于諸多領域.這類分數(shù)階導數(shù)(如Riemann-Liouville型和Caputo型分數(shù)階導數(shù))及其對應的分數(shù)階積分被賦予奇異核,有利于刻畫具有記憶效應的演化過程[1],但核的奇異性給問題的數(shù)學處理帶來困難.許多動力學過程的延遲記憶效應可用含非奇異核的積分進行研究,如Stanislavsky等[2]和Harko等[3]利用含非奇異指數(shù)核的積分對這類過程進行了建模.因此,根據(jù)不同的應用場景和約束條件,經(jīng)典的分數(shù)階導數(shù)和積分應作進一步推廣.目前,新引進的含非奇異核的分數(shù)階導數(shù)和積分主要分為2類:非奇異指數(shù)核,以Caputo-Fabrizio型分數(shù)階導數(shù)為代表[4];非奇異Mittag-Leffer核,以Atangana-Baleanu型分數(shù)階導數(shù)為代表[5].含非奇異核的分數(shù)階導數(shù)及分數(shù)階微分方程已成為一個熱門的研究領域[6-9].

在Caputo等[4]和Atangana等[5]給出的含非奇異核分數(shù)階導數(shù)的定義中,導數(shù)的階介于0～1之間,這一點會影響這類導數(shù)的應用范圍.為此,Abdeljawad[10-11]將文獻[4-5]中的定義推廣到高階情形.其中,Abdeljawad[10]定義了高階Caputo-Fabrizio型分數(shù)階導數(shù)與積分,系統(tǒng)地研究了它們的主要性質(zhì).他們還研究了幾類初值與邊值問題解的存在性,特別地,建立了一類階介于2～3之間的線性分數(shù)階方程邊值問題解的Lyapunov型不等式.值得注意的是,雖然Abdeljawad[10]給出了原邊值問題等價的積分方程,但是積分核并非原問題真正意義上的格林函數(shù),因此沒能給出這類邊值問題解的存在性結果.筆者擬在文獻[10]的基礎上,探討以下這一類含高階Caputo-Fabrizio型分數(shù)階導數(shù)的分數(shù)階微分方程兩點邊值問題正解的存在性:

(1)

其中f:[0,1]×[0,+∞)[0,+∞),2<α≤3.

2 預備知識

定義1[1]設y∈L1[a,+∞),α>0,定義y的α階Riemann-Liouville型分數(shù)階積分為(aIαy)(t),

(2)

(3)

其中B(α)為規(guī)范化函數(shù),B(0)=B(1)=1.

定義2可以通過歸納推廣到高階情形.

(4)

其中β=α-n.

命題1[10]定義3中的導數(shù)與積分有以下關系:

(5)

(6)

引理1設h∈L1(0,1),α∈(2,3],則問題

(7)

存在唯一解

其中格林函數(shù)

(8)

(9)

再由(2),(3),(4)式,對(9)式進行等價變形處理,得

(10)

由邊界條件,可確定常數(shù)

將c1及c2代入(10)式中,進一步變形可得

其中

G1(t,s)=2(1-β)(1-s)+βt(1-s)2-2(1-β)(t-s)-β(t-s)20≤s≤t≤1,

G2(t,s)=2(1-β)t(1-s)+βt(1-s)20≤t≤s≤1,

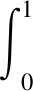
為了給出格林函數(shù)G(t,s)的基本性質(zhì),先引入相關參數(shù)和函數(shù).記

引理2θ(t)Φ(s)≤G(t,s)≤Φ(s).

證明一方面,由(8)式可知,對于?s,t∈[0,1],有

2B(β)G(t,s)≤2(1-β)t(1-s)+βt(1-s)2≤2(1-β)(1-s)+

β(1-s)=(2-β)(1-s)≤2(1-s),

于是導出G(t,s)≤Φ(s).

另一方面,當0≤t≤s≤1時,

2B(β)G(t,s)=2(1-β)t(1-s)+βt(1-s)2≥2σt(1-t)(1-s)≥σt(1-t)(1-s),

即θ(t)Φ(s)≤G(t,s);當0≤s≤t≤1時,

2B(β)G(t,s)=2(1-β)t(1-s)+βt(1-s)2-2(1-β)(t-s)-β(t-s)2=

(1-t)(2(1-β)s+β(t-s2))≥σ(1-t)(t+2s-s2)≥

σt(1-t)(1-s)),

即θ(t)Φ(s)≤G(t,s).證畢.

3 主要結果及其證明

基本假設:

(H)f為[0,1]×[0,+∞)上非負連續(xù)二元函數(shù),且關于2個變元具有連續(xù)偏導數(shù).

P={u∈B:u(t)≥θ(t)‖u‖,t∈[0,1]}.

給定正數(shù)r,定義B中的開球Ωr,Ωr={u∈B:‖u‖

(11)

條件(H)確保算子A有意義且具有以下幾個性質(zhì):

引理4若條件(H)滿足,則A(P)?P.

證明對于?u∈P,由(11)式及引理2,可得

及

這導出(Au)(t)≥θ(t)‖Au‖,因此A(u)∈P.再由u的任意性,可得A(P)?P.證畢.

在條件(H)下,用標準化的過程和方法不難證明引理5,在此省略.

由引理1及引理2,可得以下結果:

引理6若條件(H)滿足,則函數(shù)u(t)為邊值問題(1)的正解,當且僅當它是算子A在錐P中的不動點.

定理1若條件(H)滿足,且

則邊值問題(1)至少存在1個正解.

f(t,u(t))≥ρu(t)t∈[0,1],u∈P∩?Ωr1.

(12)

由(11),(12)式及引理2,可得以下估計:對于?t∈[τ,1/2],u∈P∩?Ωr1,有

因此,對于?u∈P∩?Ωr1,有‖A‖≥‖u‖.

記ρ2=max{f(t,u):t∈[0,1],u∈[0,ρ1]},則由已得到的估計,進一步可得

f(t,u)≤εu+ρ2t∈[0,1],u≥0.

(13)

因此,對于?u∈P∩?Ωr2,有‖A‖≤‖u‖.

類似地,可證明以下結果:

定理2若條件(H)滿足,且

則邊值問題(1)至少存在1個正解.