A PRIORI BOUNDS AND THE EXISTENCE OF POSITIVE SOLUTIONS FOR WEIGHTED FRACTIONAL SYSTEMS?
Pengyan WANG(王朋燕)Pengcheng NIU(鈕鵬程)
School of Mathematics and Statistics,Northwestern Polytechnical University,Xi’an 710129,China
E-mail:wangpy119@126.com;pengchengniu@nwpu.edu.cn
Abstract In this paper,we prove the existence of positive solutions to the following weighted fractional system involving distinct weighted fractional Laplacians with gradient terms:Here(??)denote weighted fractional Laplacians and ??Rnis a C2bounded domain.It is shown that under some assumptions on hi(i=1,2),the problem admits at least one positive solution(u1(x),u2(x)).We first obtain the a priori bounds of solutions to the system by using the direct blow-up method of Chen,Li and Li.Then the proof of existence is based on a topological degree theory.
Key words weighted fractional system;gradient term;existence;a priori bounds
1 Introduction
The fractional Laplacian arises from purely jump L′evy processes.It also appears in stochastic control problems[21].The weighted fractional Laplacian is a particularly relevant kind of L′evy process:the α-stable L′evy processes[27].In recent years,since the work of Caffarelli and Silvestre[4],weighted fractional Laplacians have been extensively studied.For other results on weighted fractional Laplacian equations,we refer readers to[16]for the interior and boundary H¨older regularity of the solution,[7]for a Liouville-type theorem and fundamental solution,and[34]for the symmetry and monotony of solutions.Recently,Barrios et al.[1]showed the existence of positive solutions for the following weighted fractional equation with gradient terms:

Subsequently,Quaas and Xia[30]proved some existence results of positive solutions for fractional elliptic equations with gradient terms
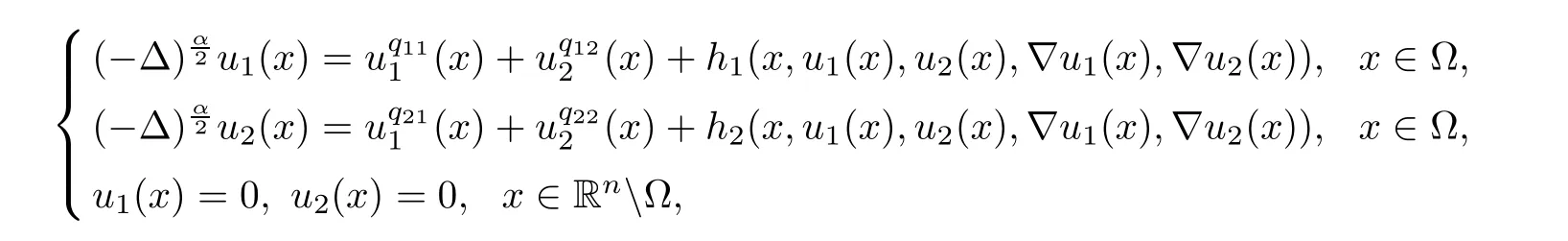
under some assumptions on hi,i=1,2.
Inspired by the works above,we first investigate the a priori bounds and existence results of positive solutions for the following weighted fractional system without gradient terms:

In addition,we will require the weighted fractional operators to be elliptic,which means that there exist two positive constants m0≤M0such that

We also assume that the weighted function ai:Rn→R satis fies ai(x)=ai(|x|)and

in the sense of distribution.
If a1(x)≡1,then(??)becomes the standard fractional Laplacian(??).There have seen a series of results on fractional equations during the last decade;see[2,6,9,12,13,15,23,28,29,31,32,35,38]and the references therein.The difficulty in studying system(1.1)is that the system does not have a variational structure,therefore we will use topological methods to prove the existence of positive viscosity solutions.The main difficulty when we use topological methods is to obtain a priori bounds.To do this,the first step is to show that all positive solutions of(1.1)are a priori bounded under several expected restrictions on fiand qij,i,i=1,2.Instead of the conventional extension method introduced by Caffarelli and Silvestre[3],we work directly on the nonlocal operator.Our a priori bounds for the solutions to(1.1)are established via the blow-up method in[11]and the Liouville theorems of viscosity solutions for fractional elliptic equations and systems in[1,11].
In this paper,we consider the viscosity solution of system(1.1).For the given domain ?in Rn,recall that a continuous pair(u1,u2):Rn×Rn→R×R is a viscosity supersolution(subsolution)to(1.1)if

If(u1,u2)is both a viscosity supersolution and a viscosity subsolution to(1.1),we say that(u1,u2)is a viscosity solution to(1.1).Hence,in this context,a solution of system(1.1)is(u1,u2)∈C1(?)∩C(Rn)vanishing outside ? and satisfying the system in the viscosity sense.One knows that(u1,u2)∈C1(?)∩C(Rn)and u1,u2are compactly supported in ? to ensure that(u1,u2)satis fies the integrability conditions.
Our first two main results are as follows:
Theorem 1.1Assume that ??Rnis a C2bounded domain and that ai(x)are measurable functions satisfying(1.4)and(1.5).Suppose that
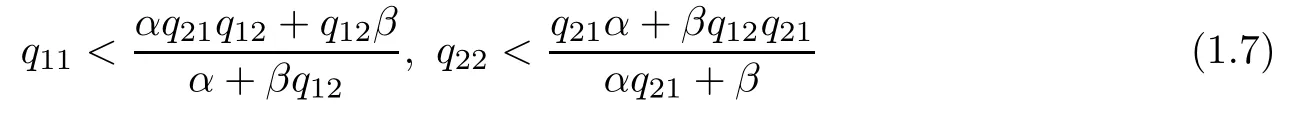
and fi∈C(×R×R)are nonnegative and satisfy the growth restrictions
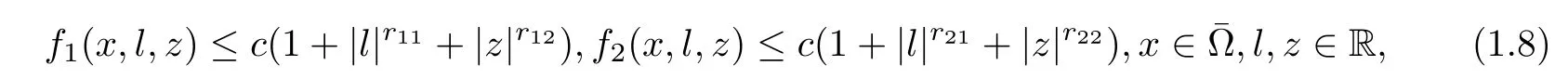
where c>0 and 1
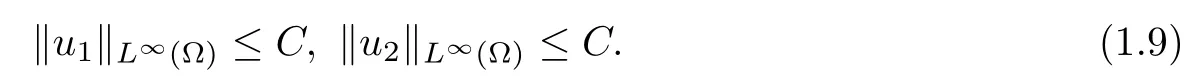
Theorem 1.2Under the hypotheses of Theorem 1.1,system(1.1)possesses at least a positive viscosity solution.
Next,we will study the a priori bounds and the existence of positive solutions for the following nonlinear equations with gradient terms:
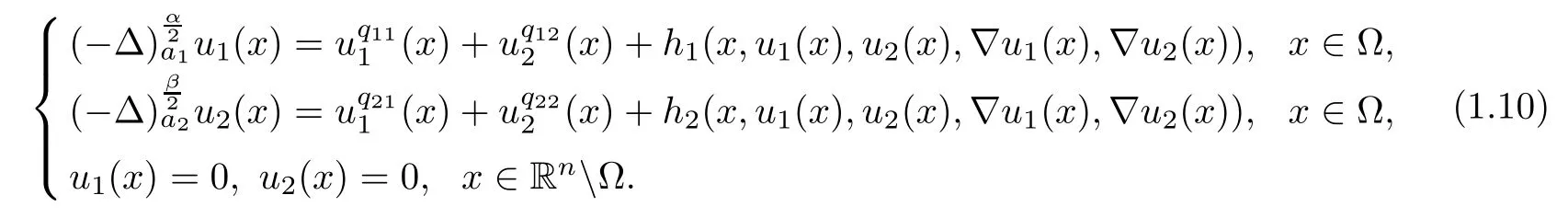
Here h1and h2are perturbation terms which are small in some sense.For the type of nonlocal equation that we are analyzing,a natural restriction made in order to ensure that the gradient is meaningful is that 1<α,β<2;see[1].In order to obtain the a priori bounds of system(1.10),some norms with weights depending on the distance from the boundary of domains have been used to estimate the gradients of sequences of solutions that appear in the blow-up method.Let
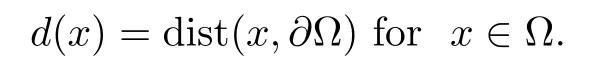
It is well known that d(x)is Lipschitz continuous in ? with a Lipschitz constant 1 and a C2function in a neighborhood of??;we modify it outside this neighborhood to make it a C2function(still with the Lipschitz constant 1),and we extend it to be zero outside ?.
For σ∈R and u∈C(?),we de fine([20],Chap.6)as
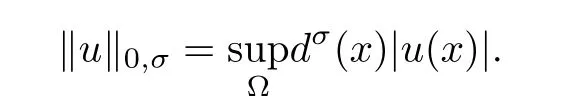
When u∈C1(?),we also de fine

For related nonlinear equations involving gradient terms?u,we refer readers to[36]for the symmetric property,[33]for Lewy-Stampacchia type estimates,[14]for maximum principles,and[24,30]forca priori bounds and existence,and references therein.Some papers on a priori bounds and existence are[10,17–19,37].
We will prove the following theorems.
Theorem 1.3Let ??Rnbe a C2bounded domain and let ai(x)be measurable functions satisfying(1.4)and(1.5).Assume that n>2,1<α,β<2,qijsatisfy(1.7)and
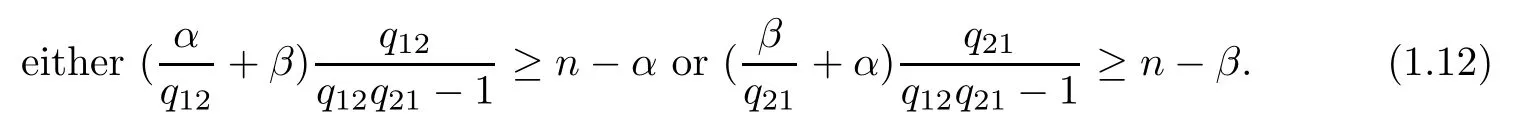
Suppose that hi∈C(?×R×R×Rn×Rn)are nonnegative and satisfy
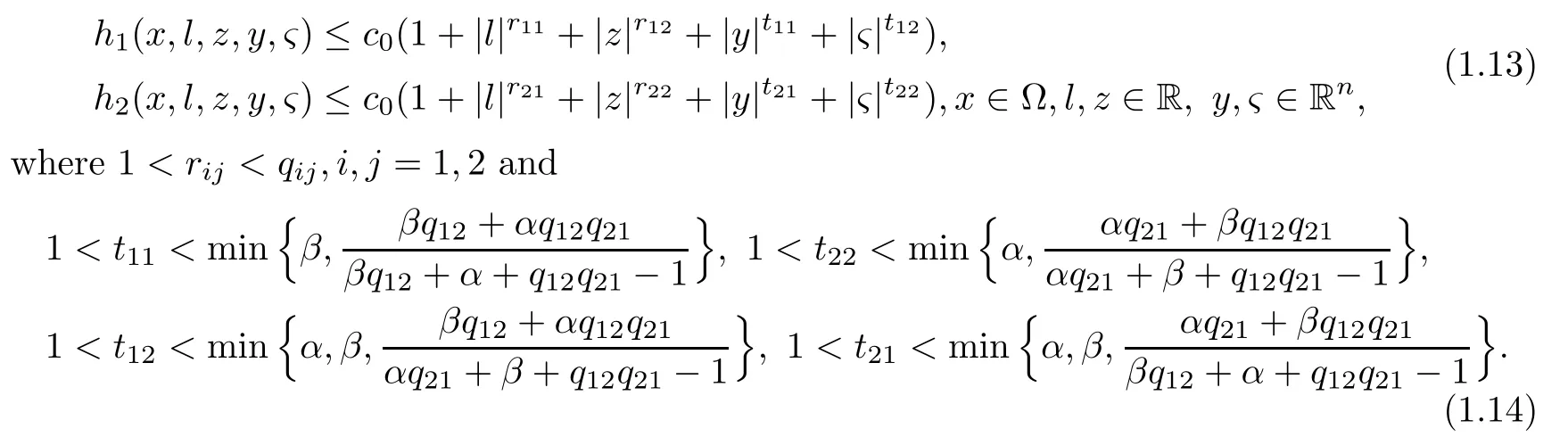
Then there exists a constant C>0,independent of u1,u2,such that for every positive viscosity solution u1,u2of(1.10),we have

where
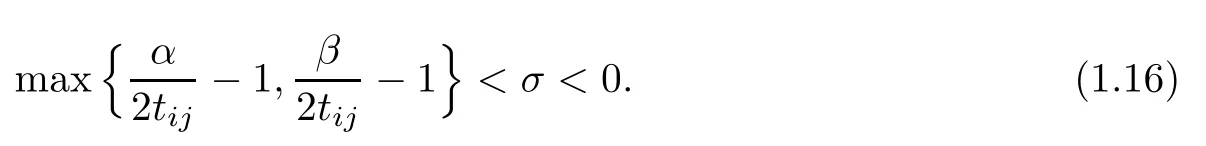
Theorem 1.4Under the hypotheses of Theorem 1.3,system(1.10)possesses at least a positive viscosity solution.
Remark 1.5Compared with[30],our results are about a distinct weighted fractional system with gradient terms.When α=β and a1=a2≡1,Theorems 1.2 and 1.4 include Theorems 1.1 and 1.2 in[30].Our results also extended the results of[1]and[24].
This paper is organized as follows:in Section 2,we give some regularity results,a convergence theorem and Liouville-type theorems of nonlocal systems needed for our arguments.In Section 3,a priori bounds for systems(1.1)and(1.10)by a direct blow-up method are obtained.Section 4 is devoted to the proofs of Theorems 1.2 and 1.4 by using the topological degree theory.
Throughout the paper,C will be a positive constant which can be different from line to line,and only the relevant dependence is speci fied.
2 Preliminaries
In this section,we collect several statements regarding the construction of suitable barriers and the interior regularity of equations related to(1.1)and(1.10).For convenience,let us denote
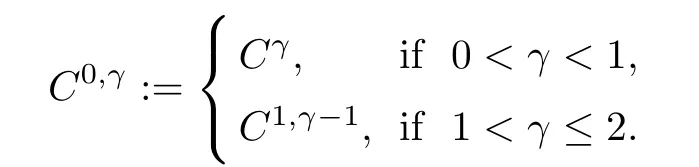
We first describe two Liouville-type theorems of the limit systems of(1.1)and(1.10)in the whole space and half space.
Theorem 2.1(see[25]) Assume that n≥2,0<α,β<2,p,q>0 and pq>1.Then,the only non-negative viscosity super-solution of the system
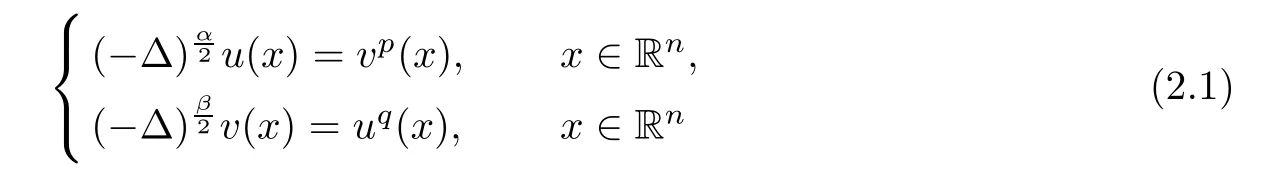
is trivial if and only if the following condition holds:
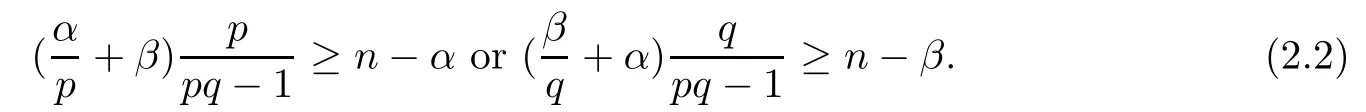
Theorem 2.2(see[25]) Assume that n>2,0<α,β<2,p,q>0 and pq>1.If(2.2)holds,then the only non-negative viscosity bounded solution of the system
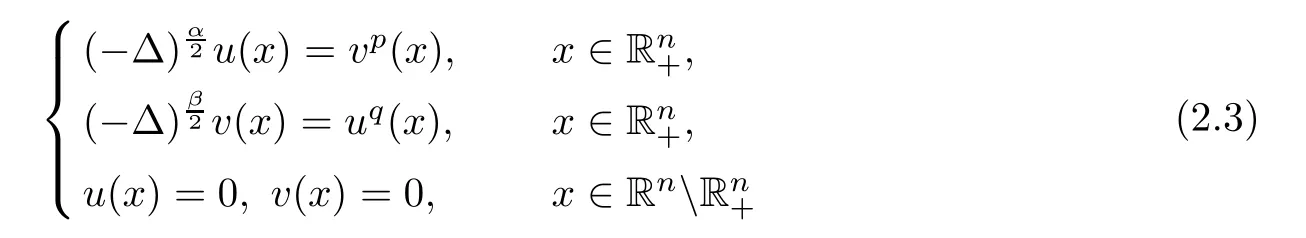
is trivial.
We now present a convergence result for the weighted fractional Laplacian.
Lemma 2.3(see[5]) Suppose that 0<α<2.Let{uk},k∈N be a sequence of functions that are bounded in Rnand continuous in ?,where fkand f are continuous in ? such that
(2)uk→u locally uniformly in ?;
(3)uk→u a.e.in Rn;
(4)fk→f locally uniformly in ?.Then(??)u≤f in ? in the viscosity sense.We recall two Cγestimates.
Proposition 2.4(see[16]) Assume that α+γ(γ∈(0,))is not an integer.If f(x)∈Cθ(B3),u(x)∈L∞(Rn)solves
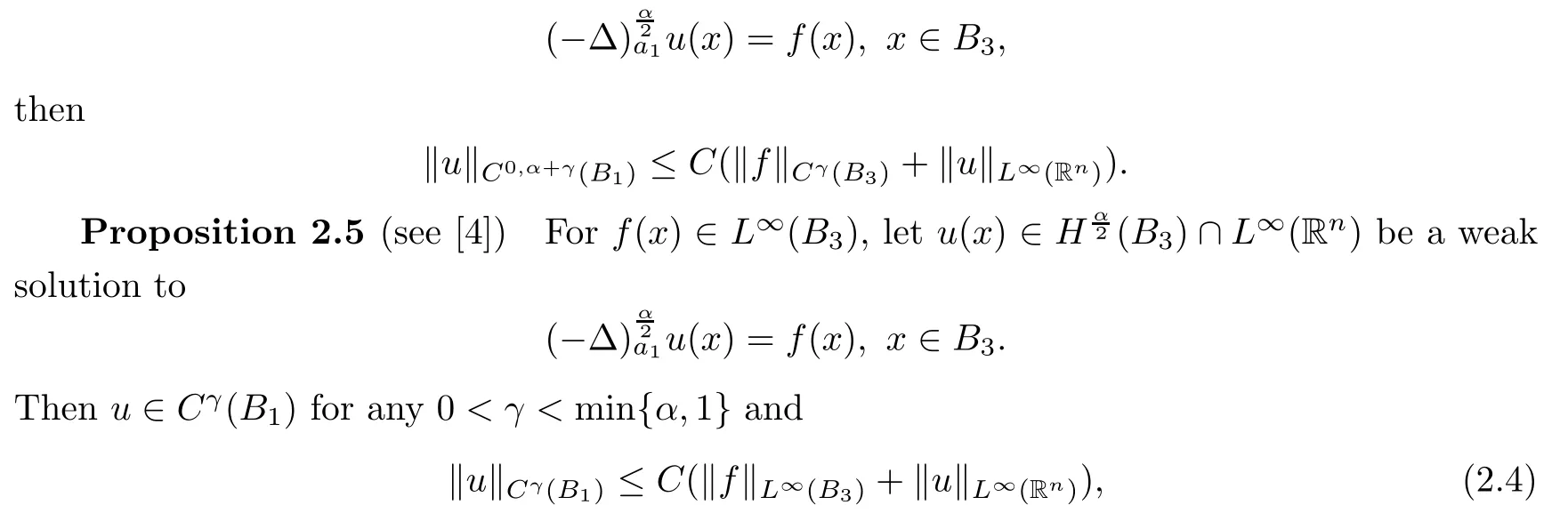
for a suitable C>0 depending on n,α and γ.
Lemma 2.6(see[22]) Assume that α∈(1,2).Suppose that u is a viscosity solution of
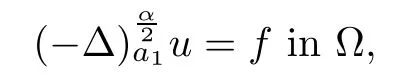
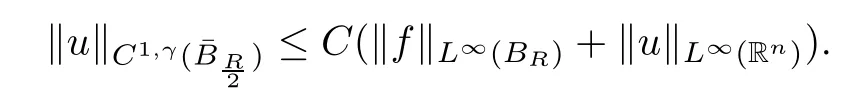
The following estimates are proven in[1]for the Dirichlet problem:
Lemma 2.7(see[1]) Assume that ? is a C2bounded domain,that 0<α<2,and that a is a measurable function satisfying(1.4)and(1.5).Let f∈C(?),satisfying
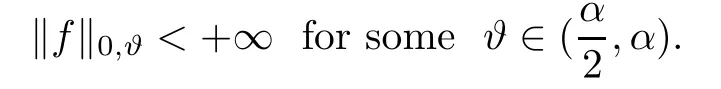
Then the problem
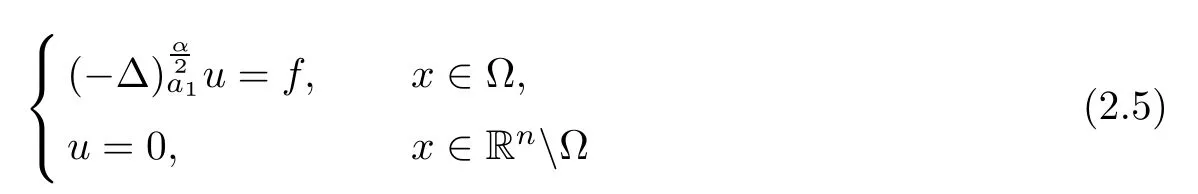
admits a unique viscosity solution.Moreover,there exsits a positive constant C such that

Finally,if f≥0 in ?,then u≥0 in ?.
The following estimate is about the gradient of the solution of(2.5)when α>1:
Lemma 2.8(see[1]) Assume that ? is a smooth bounded domain and α>1.Then there exists a constant C0which depends on n,α,m0and M0but not on ? such that,for every ?∈(,α)and f∈C(?)with‖f‖0,??α+1<+∞,the unique solution u of(2.5)satis fies
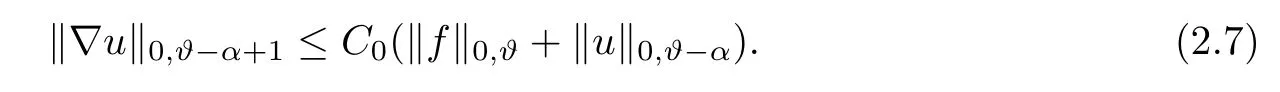
The next lemma is intended to consider the constant in(2.6)when we study problem(2.5)in expanding domains,since in general it depends on ?.This is a crucial point for the scaling method to work properly in our setting.From the lemma,we know that the constant in(2.6)for the solution of(2.5)posed in ?μ:={x∈Rn|ξ+λx∈?}will depend on the domain ?,but not on the dilation parameter λ.
Lemma 2.9(see[1]) Assume that ? is a C2bounded domain,that 0<α<2 and that a1(x)are measurable functions satisfying(1.4)and(1.5).For every θ∈(,α)andμ0>0,there exist C0,δ>0 such that
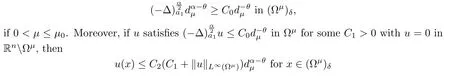
for some C2>0 only depending on α,δ,θ and C0.
Finally,we recall the following maximum principle:
Lemma 2.10(see[1]) Let a1be a measurable function satisfying(1.4).Assume that u(x)∈C(Rn),and that u(x)>0 in Rnsatis fies(??)u(x)≥0 in the viscosity sense in ?,Then,u(x)>0 or u(x)≡0 in ?.
3 A Priori Bounds
This section is devoted to the proof of a priori bounds for positive solutions to problems(1.1)and(1.10).
Proof of Theorem 1.1Assume that positive solutions of(1.1)do not have an a priori bound;that is,there exists a sequence(u1k,u2k)of positive solutions to(1.1)such that at least one of the sequences u1kand u2ktends to in finity in the L∞-norm.Without loss of generality,suppose that there exists a sequence of solutions{u1k}to(1.1)and a sequence of points{xk}?? such that

Let τ1,τ2be fixed positive constants to be chosen later.We set
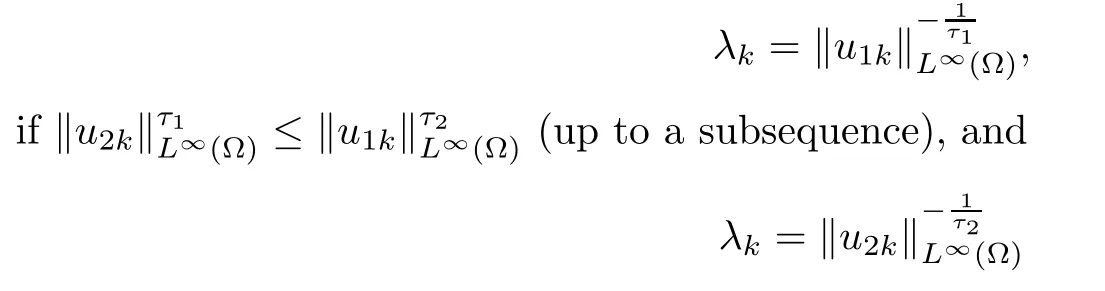
otherwise.
Note that λk→0 as k→∞.Let xk∈? be a point where u1kassumes its maximum.The functions
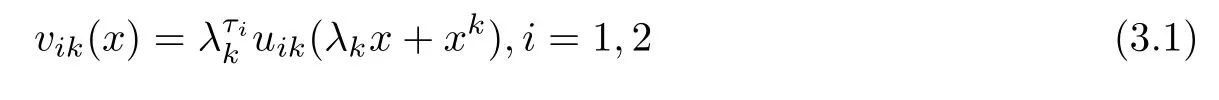
satisfy v1k(0)=1 and 0≤vik≤1 in ?k.One also veri fies that the functions v1k,v2ksatisfy

By d(x)=dist(x,??)for x∈? and compactness we can assume that{xk}tends to some point x0∈ˉ?.We will carry out the proof using a contradiction argument while exhausting all three possibilities.
Case 1xk→x0∈? or=+∞.
It is not difficult to see that
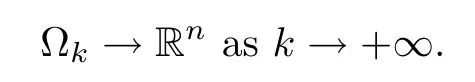
Because of 0≤vik≤1,it follows that v1kand v2kare uniformly bounded,and the right hand side in(3.2)is uniformly bounded,so we may use(2.4),Ascoli-Arzel′a’s theorem,the regularity of solutions to weighted fractional Laplace equations and a diagonal argument to obtain that vik→vi(i=1,2)locally uniformly in Rn.We will claim that there exist nonnegative functions v1(x)and v2(x)(0)such that,as k→+∞,
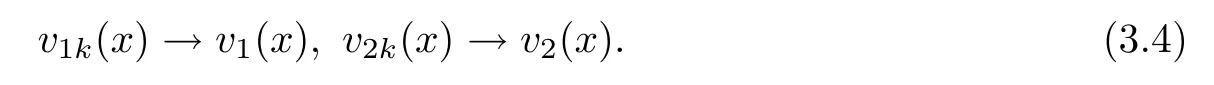
Let us postpone the proof of(3.4)for a moment.
Passing to the limit in(3.2)and using the fact that aiis continuous at zero with ai(0)=1,we see by Lemma 2.3 that(v1,v2)solves
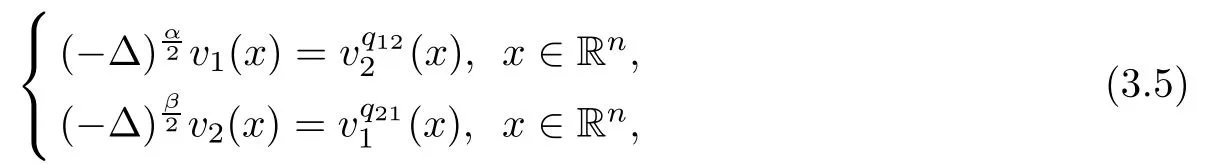
in the viscosity sense.
By standard regularity(see Proposition 2.4),one obtains v1∈Cα+γ1(Rn)and v2∈Cβ+γ2(Rn)for some γi∈(0,1).Moreover,noting that v1(0)=1,the strong maximum principle(Lemma 2.10)implies that v1>0,v2>0.Then,by a bootstrapping argument and Proposition 2.4,we would actually have that v1,v2∈C∞(Rn).However,since q12q21>1 and q12,q21satis fies(1.12),while contradicts Theorem 2.1.Hence this case cannot happen.
Now we will prove(3.4)in a way similar to[35].We need to establish a uniform C0,α+θestimate for v1kin a neighborhood of any point x∈Rn,which is independent of k and x.This is done in two steps.We first obtain a Cθestimate(0<θ<1),and then boost Cθup to C0,α+θby using the equation satis fied by v1k(x).
Since v1k(x)and v2k(x)are positive bounded solutions to system(3.2),we have|v1k(x)|≤C,|v2k(x)|≤C,

Similarly to Case 1,here we are able to establish the existence of functions v1,v2and subsequences of{v1k},{v2k}such that,as k→+∞,
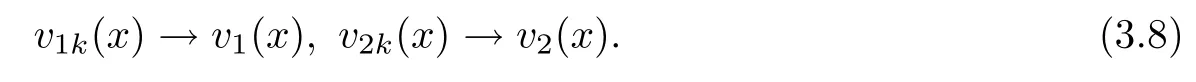
Therefore,we employ the regularity Theorem 2.3 to obtain that v1k→v1and v2k→v2on compact sets of,where(v1,v2)veri fies that 0≤v1,v2≤1 inand solves
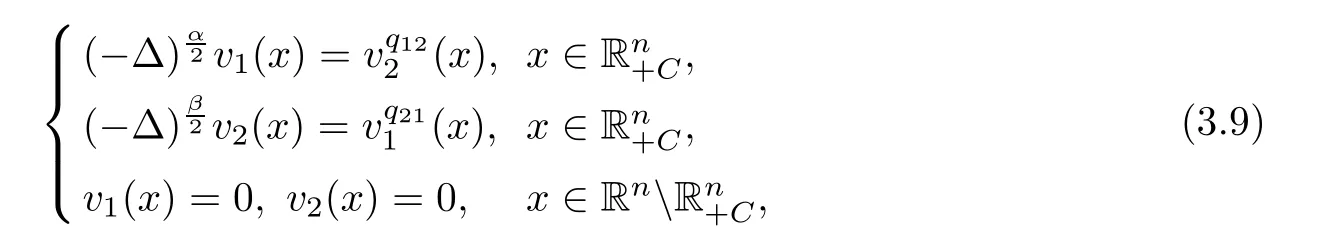
in the viscosity sense.It is known that(3.9)has no positive viscosity solution(see Theorem 2.2).Meanwhile,we have
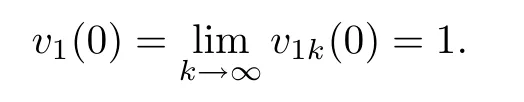
This is a contradiction.
It remains to prove(3.8).Let D1=B1(0)∩{xn>0}.Then,in a fashion similarly to the argument in Case 1,we can show that there exists a converging subsequence of{v1k}(still denoted by{v1k})such that


This implies that|pk|is bounded from below,and thus that C>0.This rules out the possibility of Case 3.
Theorem 1.1 is proved.
As mentioned before,we need to consider weighted norms;this presents some problems,since the scaling needed near the boundary is not the same as in the interior.Therefore,before giving the proof of Theorem 1.3,we first obtain rough bounds for all solutions of the equation which are universal,in the spirit of[26].
Lemma 3.1Assume that ? is a C2(not necessarily bounded)domain and that ai(x)are measurable functions satisfying(1.4)and(1.5).Suppose that 1<α,β<2.Then there exists a positive constant C=C(n,s,rij,tij,c0,?)(where rij,tijand c0are given in(1.13))such that,for every positive solution(u1,u2)∈C1(?)∩L∞(Rn)satis fies system(1.10)in the viscosity sense in ?,we have

ProofAssume that the conclusion fails.Then,there exist sequences of positive functions u1k,u2k∈C1(?)∩L∞(Rn)and yk∈? satisfying
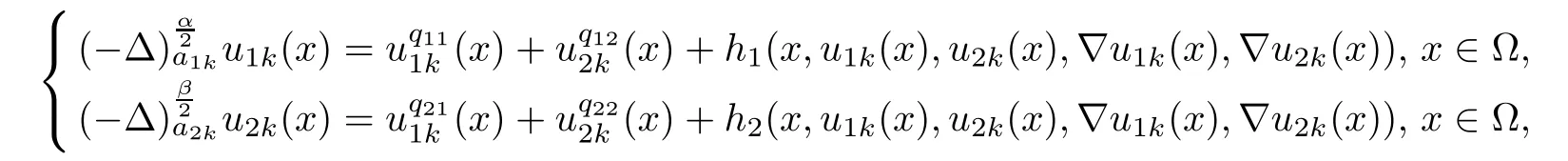
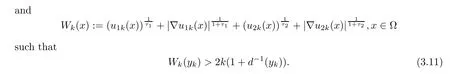
By Lemma 5.1 in[26],there exists a sequence of points xk∈? such that Wk(xk)≥Wk(yk),Wk(xk)>2k·d?1(x)and
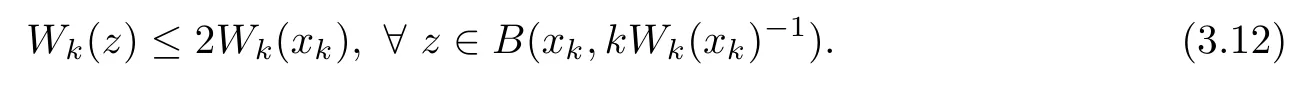
It follows from(3.11)that Wk(xk)→+∞as k→+∞.Let λk=Wk(xk)?1→0 as k→+∞,and de fine


This contradicts Theorem 2.1,since(1.12)holds.Hence we complete the proof.
Let us analyze the a priori bounds for solutions to problem(1.10).Since the expected singularity of the gradient of the solutions is near the boundary,we need to work in spaces with weights which take care of the singularity.Thus we fix σ∈(?1,0)satisfying(1.16),and let
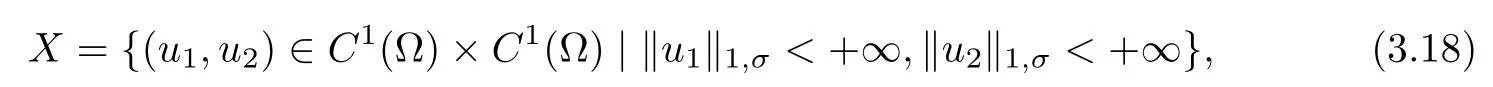
where‖·‖1,σis given by(1.11).
Proof of Theorem 1.3Assume that the conclusion of the theorem is not true.Then there exists a sequence of positive solutions of(1.10)which do not have an a priori bound;that is,there exists a sequence of positive solutions(u1k,u2k)∈X of(1.10)such that
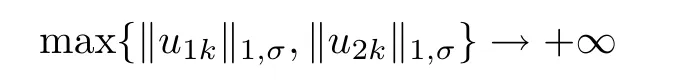
as k→∞.We may assume that
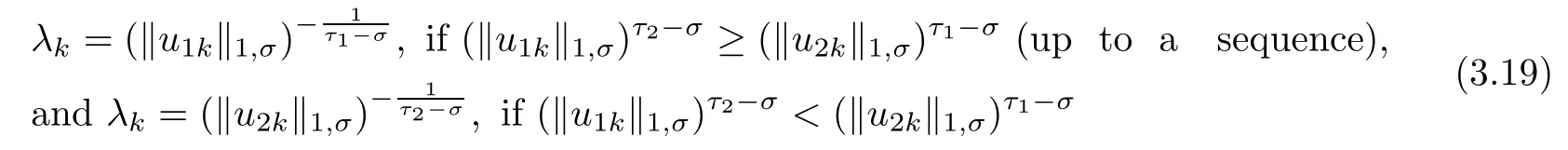
for some constants τ1,τ2>0 to be determined later.Without loss of generality,we consider the first situation.Denoting
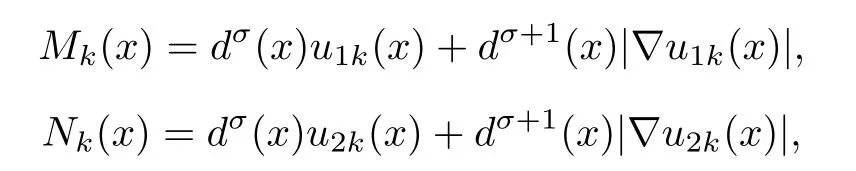
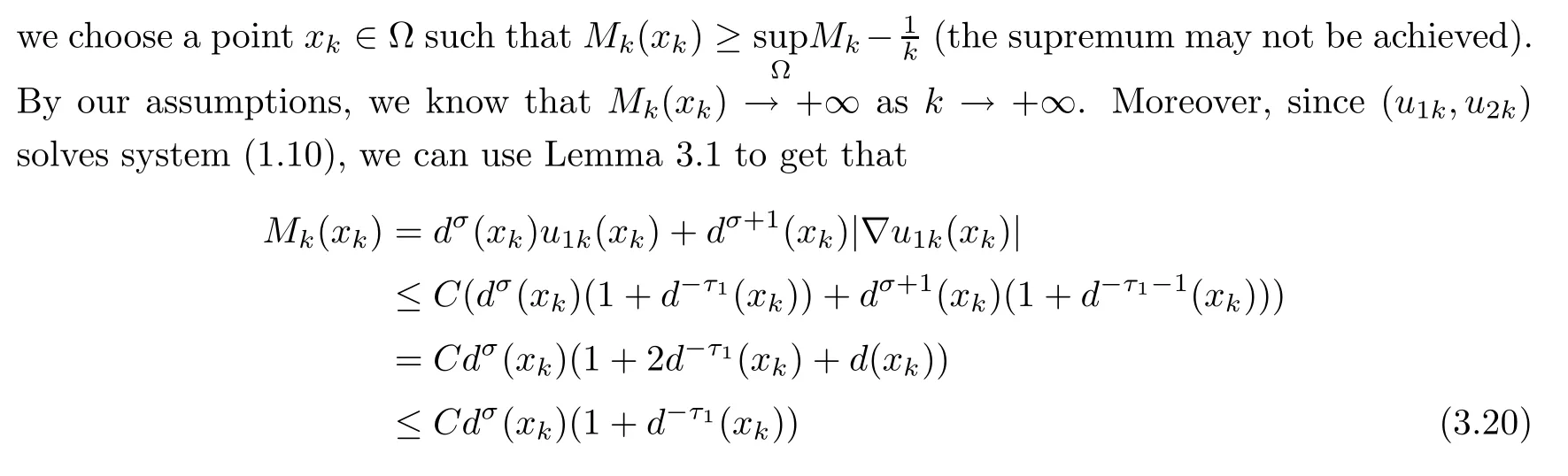
for some positive constant C independent of k,which implies that

Let ξkbe a projection of xkon??,and let


Taking(3.29)and(3.30)in(3.24),we deduce that

where C is also independent of k.This implies that dk(yk)is bounded away from zero.Hence|yk|is also bounded,since 0∈?Dk.Therefore we have that d>0,as claimed.

4 Existence of Solutions
This section is devoted to the proof of Theorems 1.2 and 1.4.Both proofs are very similar,though the proof of Theorem 1.4 is slightly more complicated.For convenience,we only prove Theorem 1.4.The proof uses the topological degree and the a priori bounds provided by Theorems 1.1 and 1.3.The most essential tool is the following well-known result:
Theorem 4.1([8],Theorem 3.6.3) Suppose that(X,P)is an ordered Banach space,and that U?P is a bounded open set that contains 0.Assume that there exists ρ>0 such that Bρ(0)∩P?U and T:P is compact and satis fies that(a)for any x∈P with|x|=ρ,and λ∈[0,1),xλTx;(b)there exists some y∈P{0},such that x?Txty for any t≥0 and x∈?U.Then T possesses a fixed point on,where Uρ=UBρ(0).
Consider the Banach space
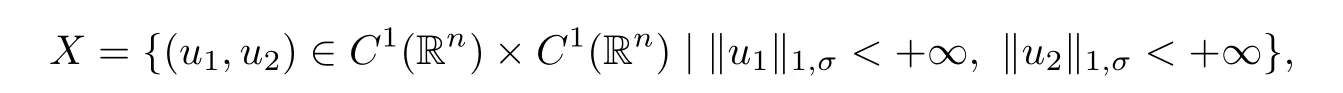
with the norm
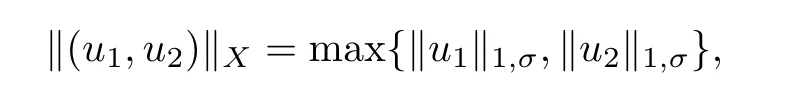
and de fine the positive cone

Observe that for every(u1,u2)∈P,

where the positive constant C depends on the norms‖u1‖1,σand‖u2‖1,σ.Moreover,as in the proof of Theorem 1.3,we know that
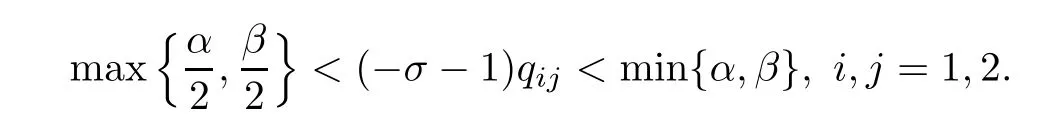
Hence,applying Lemma 2.7 to the system
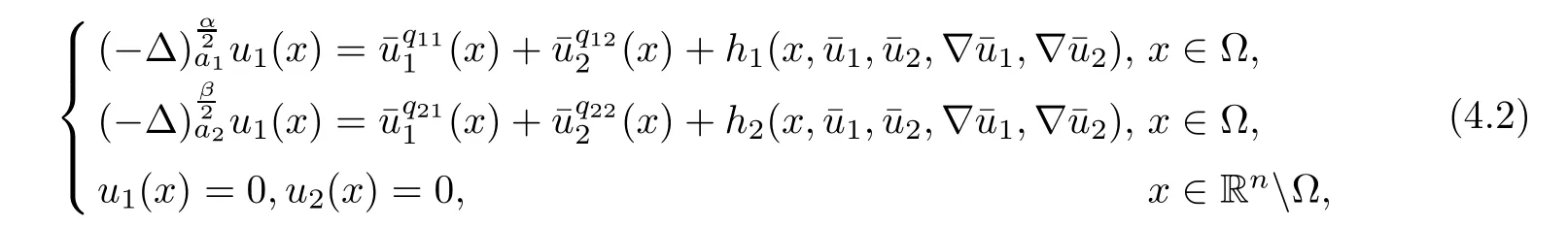
where h1and h2satisfy(1.13),it follows that system(4.2)has a unique nonnegative solution(u1,u2)with‖u1‖0,σ<+∞,‖u2‖0,σ<∞.Therefore,(u1,u2)∈X.We de fine
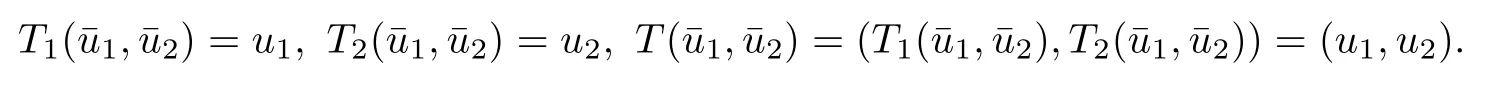
It is clear that nonnegative solutions of(1.10)in X coincide with the fixed points of this operator T.
Unlike(??)α/2,the corresponding inverse operator of T can sometimes be explicitly expressed as an integral via Green’s functions,and little is known about such expressions for the more general operatorFortunately,we can apply Lemmas 2.7 and 2.8.
Lemma 4.2For α,β∈(0,2),the operator T:P→P is compact.
ProofWe start with the continuity of T.Let{(u1k,u2k)}?P be solutions for(1.10).Suppose that u1k→u1and u2k→u2in X.In particular,u1k→u1,u2k→u2,?u1k→?u1and?u2k→?u2uniformly on compact sets of ?,so the continuity of hiimplies that
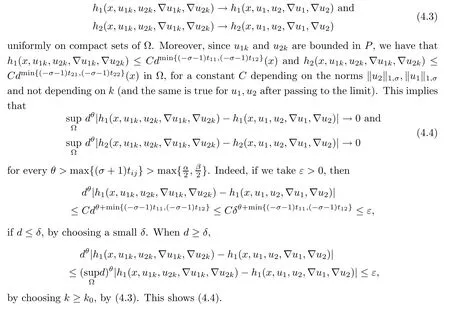
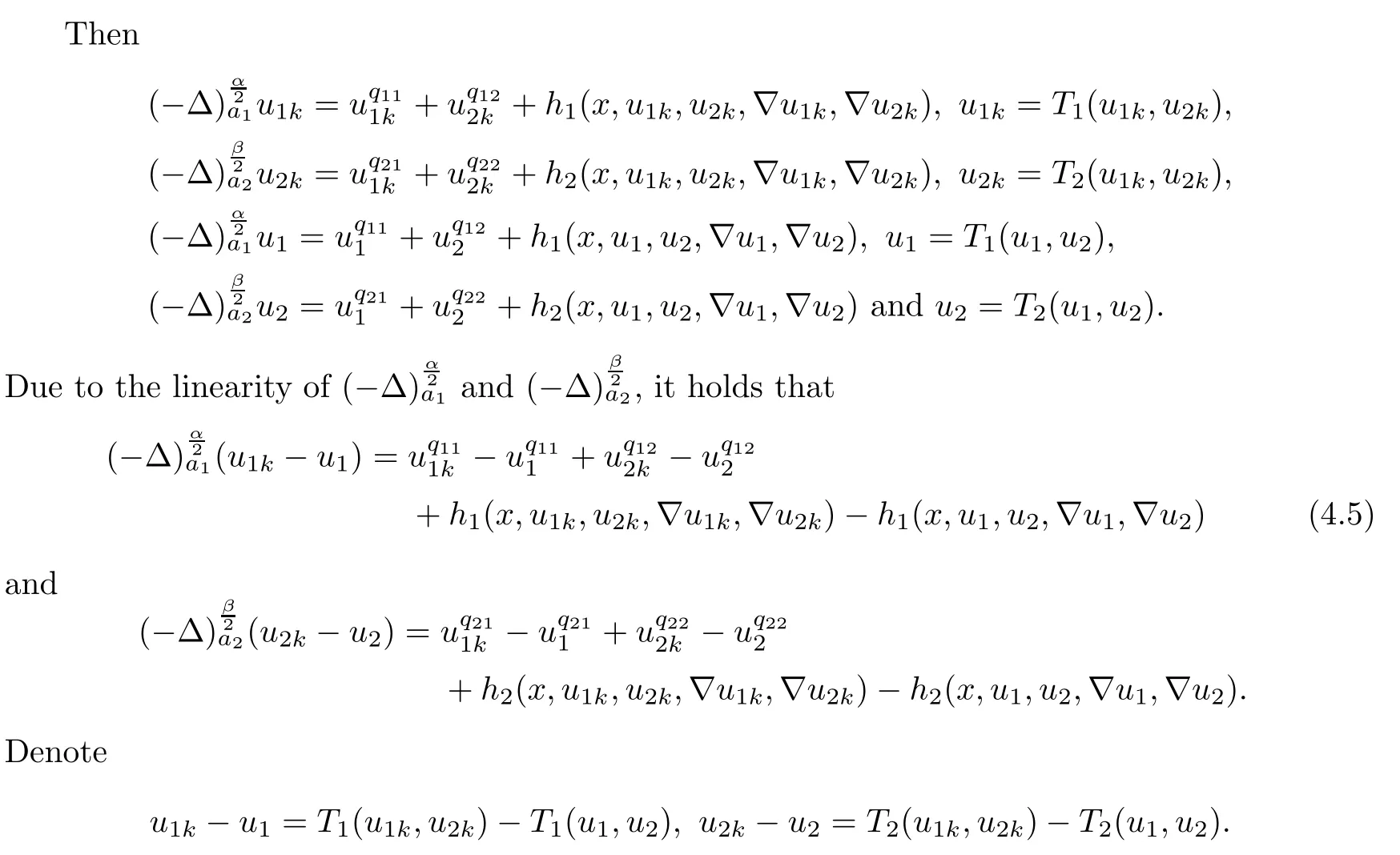
Applying Lemmas 2.7 and 2.8 to(4.5),we have,for every max{(σ+1)tij}<θ The desired conclusion follows by choosing θ such that This proves the continuity of T. Next we show that T is compact.Suppose that{(u1k,u2k)}?P is bounded in X;namely,that‖u1k‖1,σ≤C,‖u2k‖1,σ≤C.We also have(4.1)in ?.By Lemma 2.6,we obtain that,for every ?′???,the C1,γnorm of T1(u1k,u2k)and T2(u1k,u2k)in ?′is bounded.Therefore,we may assume,by passing to a subsequence,that u1k=T1(u1k,u2k)→u1,u2k=T2(u1k,u2k)→u2;i.e.,T(u1k,u2k)→T(u1,u2)in(?). From Lemmas 2.7 and 2.8,in ? we deduce that and the same estimates hold for u1and u2by passing to the limit.Hence and It is easy to see that(u1,u2)∈P.This completes the proof. Proof of Theorem 1.4In order to obtain the desired existence through Theorem 4.1,we only need to check the conditions. Let us check first(a)in Theorem 4.1.Choose ρ small enough and de fine For(u1,u2)∈?Bρ(0)∩P,suppose that we have(u1,u2)=μT(u1,u2)for someμ∈[0,1)and(u1,u2)∈P.Since(u1,u2)is a solution of the system we get,by(1.13),that the right hand sides of the equations in(4.6)can be bounded by Here we used the fact that max{?σ?α,?σ?β} Now we check(b)in Theorem 4.1.Take(?,ψ)∈P,? and ψ as the corresponding unique solutions for the following equations: and We want to prove that there are no solutions in P to the equation if t is large enough.This is equivalent to proving that there are no positive solutions to the following system: When t≤C0,we have and Since h1(x,u1,u2,?u1,?u2)+t and h2(x,u1,u2,?u1,?u2)+t also satisfy condition(1.13)for t≤C0,we can apply Theorem 1.3 to obtain the a priori bounds of the solutions for(4.18)and(4.19).Thus there exists R>ρ such that‖(u1,u2)‖X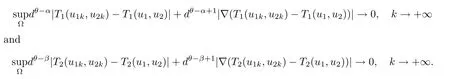


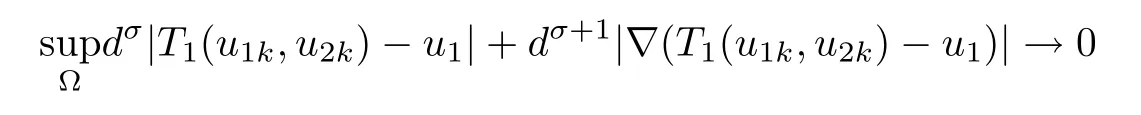
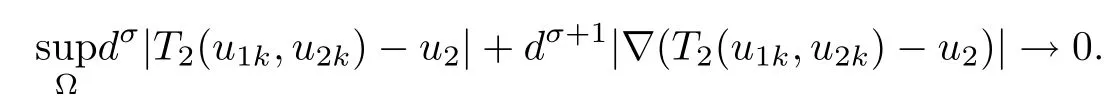

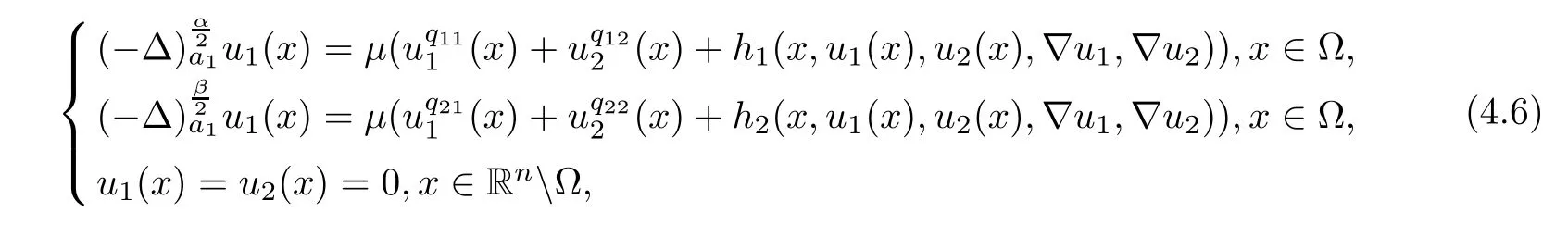
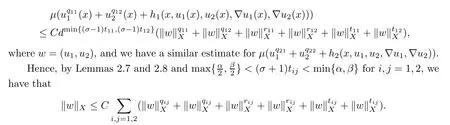

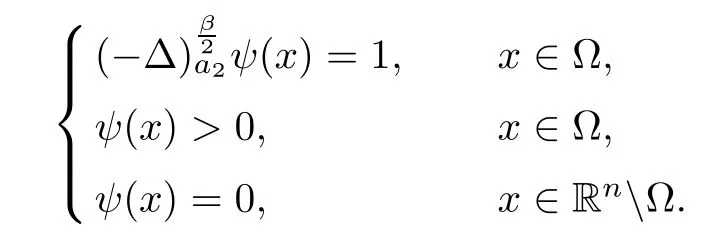
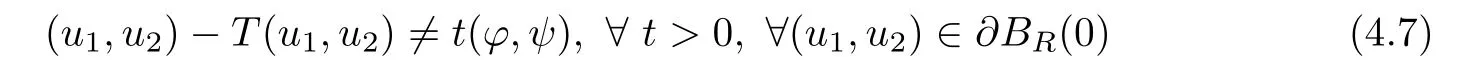

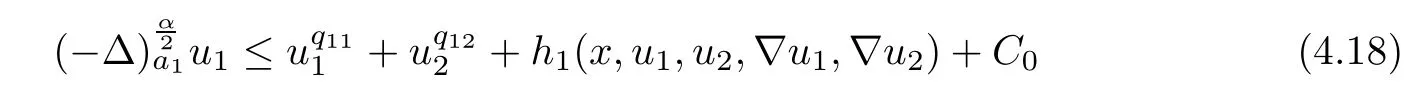
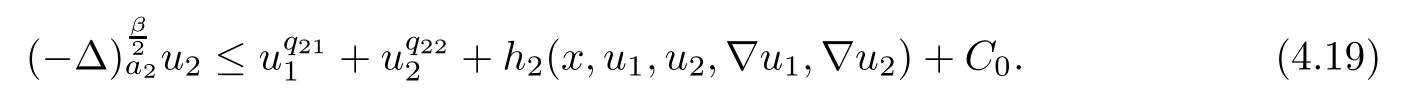
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
