A PENALTY FUNCTION METHOD FOR THE PRINCIPAL-AGENT PROBLEM WITH AN INFINITE NUMBER OF INCENTIVE-COMPATIBILITY CONSTRAINTS UNDER MORAL HAZARD?
Jia LIU(劉佳)
School of Economics and Management,Wuhan University,Wuhan 430072,China
E-mail:liujia.06@163.com
Xianjia WANG(王先甲)
School of Economics and Management,Wuhan University,Wuhan 430072,China Institute of Systems Engineering,Wuhan University,Wuhan 430072,China
E-mail:wangxj@whu.edu.cn
Abstract In this paper,we propose an iterative algorithm to find the optimal incentive mechanism for the principal-agent problem under moral hazard where the number of agent action pro files is in finite,and where there are an in finite number of results that can be observed by the principal.This principal-agent problem has an in finite number of incentivecompatibility constraints,and we transform it into an optimization problem with an in finite number of constraints called a semi-in finite programming problem.We then propose an exterior penalty function method to find the optimal solution to this semi-in finite programming and illustrate the convergence of this algorithm.By analyzing the optimal solution obtained by the proposed penalty function method,we can obtain the optimal incentive mechanism for the principal-agent problem with an in finite number of incentive-compatibility constraints under moral hazard.
Key words principal-agent problem;mechanism design;moral hazard;semi-in finite programming problem;penalty function method
1 Introduction
In the principal-agent problem under moral hazard,the agent has private information about his personal behaviors,while the principal can only observe the results caused by the agent’s actions.In this case,the principal needs to design an incentive mechanism for all agents based on the observed results to maximize his expected pro fit.Since the agent has some private information and acts with the goal of maximizing his own expected pro fit,the purpose of designing the incentive mechanism for the principal is to maximize his own expected pro fit and to motivate the agents to act in a certain way.
The optimal incentive mechanism satis fies two kinds of constraints:the incentive-compatibility constraint and individual rationality constraint.The incentive-compatibility constraint shows that the expected pro fit obtained by the agent when he chooses the action desired by the principal is not less than that obtained when he chooses any other action.This is the motivation of the principal to design the incentive mechanism based on the agent’s actions to maximize their own pro fits.The individual rationality constraint shows that the agent’s pro fit under the optimal incentive mechanism is not less than the maximum pro fit obtained when the optimal incentive mechanism is not accepted.This is the basis for the agent to participate in the incentive mechanism.All feasible actions taken by all individuals in making decisions must satisfy these two constraints.
In the incentive mechanism design problem under moral hazard,the principal designs different payment schemes to the agent according to the observable results.Generally,it is assumed that the number of agent action pro files is finite and there are a limited number of results that can be observed by the principal.This assumption makes the number of incentive-compatibility constraints limited when the principal seeks to maximize his expected pro fit.Given the form of the optimal incentive mechanism,the problem of finding the optimal incentive mechanism can be transformed into that of solving an optimization problem with finite constraints.In this case,the Kuhn-Tucker theorem or the Lagrange method can be used to solve the optimization problem,and the optimal incentive mechanism can be obtained according to the optimal solution to this optimization problem.The vast majority of researchers study incentive mechanism design problems based on this idea.However,in practical economic and political problems,agents may have an in finite number of action pro files and there are an in finite number of results that can be observed by a principal,which makes the number of incentive-compatibility constraints in finite.At this point,the incentive mechanism design problem with an in finite number of incentive-compatibility constraints can be transformed into an optimization problem with an in finite number of constraints;this is called a semi-in finite programming problem.
The main aim of this paper is to design an iterative algorithm to find the optimal incentive mechanism for the principal-agent problem with an in finite number of constraints under moral hazard.When the number of variables increases and the number of constraints increases,the traditional method becomes too complex to find an analytic solution.Since the 1970s,there has been much development in terms of solving general mechanism design problems,and a feasible analytical framework for obtaining analytical solutions has been established.However,there are many inconveniences when there are too many variables and too many constraints,such as discussion of the complex optimality conditions used in analytical methods.Inspired by the algorithm of optimization theory,we hope to design a iterative algorithm which can solve some complex mechanism design problems.This is the main motivation of this paper.
The iterative algorithm designed in this paper is a exterior penalty function method,called the M-penalty function method,where M is the ampli fication factor for the penalty function.This algorithm is designed to transform the solving of a semi-in finite programming problem into the solving of a series of unconstrained optimization problems.By establishing a set of penalty functions,the optimal solutions of the unconstrained programming problems can be approximated to the optimal solutions of the original semi-in finite programming problems.So far,few researchers have used the optimization algorithm to find the optimal incentive mechanism of the principal-agent problem with an in finite number of constraints.
The traditional analytical method and the iterative algorithm designed in this paper have their own advantages and disadvantages.For the principal-agent problem with a simple setting,it is more convenient to use the traditional analytical method to find the optimal incentive mechanism.When the parameters become more numerous and the constraints become more complex,the traditional method is more limited and it is difficult to get the optimal solution.At this point,the iterative algorithm proposed in this paper is more conducive to solving principal-agent problems.
Since there are no additional assumptions on individual utility functions,such as satisfying convexity or concavity,the proposed iterative algorithm can solve the mechanism design problem with complex functions that cannot be solved by traditional methods.Also,because this paper does not make additional assumptions about the form of the contract of the principal,the iterative algorithm in this paper can be used for the nonlinear contract as well as for the traditional linear contract.
In order to construct an iterative algorithm to find the optimal incentive mechanism for the principal-agent problem under moral hazard,this paper transforms this principal-agent problem into a semi-in finite programming problem.Then,by designing a penalty function method for solving semi-in finite programming problems,we obtain an iterative algorithm to find the optimal incentive mechanism for this principal-agent problem.
The structure of this paper is as follows:in Section 3,the principal-agent problem with an in finite number of agent action pro files and an in finite number of observable results for the principal under moral hazard is established.In the Section 4,the principal-agent problem is transformed into a standard semi-in finite programming problem(SIP),and we propose a kind of exterior penalty function method,called the M-penalty function method,to solve this semi-in finite programming problem.In Section 5,we study the convergence of the M-penalty function method.In Section 6,a numerical example is used to illustrate the method of finding the optimal incentive mechanism of a two-person principal-agent problem under moral hazard where the agent’s action pro file is in finite and the principal can observe an in finite number of results.Finally,Section 7 offers the conclusions of this paper.
2 Related Literature
2.1 Mechanism Design Theory
The research and development of mechanism design theory includes two categories:the mechanism design problem under adverse selection and the mechanism design problem under moral hazard.
The main feature of the adverse selection model is the ex ante asymmetric information.Nature selects the type of agent,and the agent knows his own type while the principal does not.In the signaling model,in order to show his type,the agent chooses a signal and the principal signs a contract with the agent after observing the signal.In the screening model,the principal provides multiple contracts for the agent to choose,and the agent selects a suitable contract according to his or her own type and acts according to the contract(see,e.g.,[1–6]).
The main feature of the moral hazard model is the ex post information.The information is symmetrical before signing the contract.In the moral hazard with hidden action model,after signing the contract,the principal can only observe the results caused by the agent’s choice of actions and the state of the world.At this time,the principal should design incentive contracts to induce the agent to choose the most bene ficial action for the principal from the perspective of maximizing the agent’s own pro fits.In the moral hazard with hidden information model,nature chooses the state of the world,the agent observes the nature’s selection and acts,while the principal observes the agent’s actions but cannot observe the state of nature’s selection.At this point,the principal should design an incentive contract to encourage the agent to choose the best action for the principal under a given state of the world(see,e.g.,[7–10]).
There are several papers in the literature on the incentive mechanism design problem in which agents have continuous action spaces that are closely related to the present work.The main methods for dealing with such a mechanism design problem is based on the analytic method for solving the optimization problem.The basic treatment includes:(1)A discrete agent’s action space to make the incentive-compatibility constraint a finite number.In this case,the Kuhn-Tucker theorem can be used to find the optimal incentive mechanism;(2)Replacing the in finite number of incentive-compatibility constraints with relatively simple local incentive-compatibility constraints.The classic single-agent moral hazard problem already has“in finitely many actions”and thus an“in finite number of incentive-compatibility constraints”(see,e.g.,[11,12]).For example,Laffont and Martmort studied the incentive mechanism design problem in which the agents have a continuous level of effort([12]).Since the optimal solution does not necessarily exist([13]),they used this method to deal with the in finite number of incentive-compatibility constraints,and found the sufficient conditions of the optimal solution to the original principle-agent problem.
In this paper,we study the incentive mechanism design problem under moral hazard with hidden action.We use an iterative algorithm to find the optimal incentive mechanism for the principle-agent problem under moral hazard where the number of agent action pro files is in finite,and where there are an in finite number of results that can be observed by the principal.The form of the optimal payment mechanism is obtained by an iterative method,which avoids the complex optimization discussion process emerged in using analytical methods.
2.2 Semi-in finite Programming Problem
In this paper,it is found that if the number of agent action pro files is in finite and there are an in finite number of results that can be observed by the principal,the optimal incentive mechanism for this incentive mechanism design problem is the optimal solution to an optimization problem with an in finite number of constraints;this called a semi-in finite programming problem.
The semi-in finite programming problem mainly studies a constrained programming problem with an in finite number of constraints.It is applied in many fields([14]),such as in the data envelopment analysis of an in finite number of decision-making units([15]),robot trajectory planning([16]),and economic,fi nancial and engineering models([17]).
There are many algorithms for solving semi-in finite programming problems,such as the discretization method([18,19]),the homotopy interior point method([20]),the Newton method([21]),the semismooth Newton method([22]),the trust region method([23]),the augmented Lagrangian method([24]),the exact penalty method([25]),the quadratic programming-type method([26]),and the branch-and-bound method([27]).The idea of designing these methods is basically based on the idea of constructing the methods for finding the optimal solution to the nonlinear programming problem.In this paper,we also design an algorithm for solving semi-in finite programming problems based on this idea.
In this paper,a type of exterior penalty function method is proposed to solve the semiin finite programming problem;this is called M-penalty function method.The penalty function method is concise in terms of solving semi-in finite programming problems,and the exterior penalty function method is even more concise than the internal penalty function method.The reason why the internal penalty function method is not adopted here is mainly due to the selection of the initial point.The internal penalty function method needs to select the initial point that satis fies all constraints.Compared with the exterior penalty function method,it is more difficult to select the initial point of the internal penalty function method.By discussing the optimal solution obtained by the M-penalty function method,we can get the optimal incentive mechanism for incentive mechanism design problem with an in finite number of incentive-compatibility constraints under moral hazard.
3 Model
In a multi-player principal-agent game,a principal(player without private information)wants the agents(players with private information)to choose an appropriate action pro file according to the goal of maximizing his expected pro fit.The principal cannot directly observe the action pro file taken by the agents,but can only observe a certain result which is determined by the agents’action pro file and some exogenous random factors.The principal’s problem is how to design a reward or punishment contract for the agents based on the observed results to encourage them to take actions that maximize his expected pro fit.
In the principal-agent problem under moral hazard,the order of the game is:the principal proposes a payment contract,then the agent decides whether to participate or not;if he does,he makes a certain effort to act and receives a bene fit under this contract.If he does not participate,the payoffs are all zero.Each individual has the goal of maximizing his or her own return.Therefore,the level of effort taken by the agent and the payment contract proposed by the principal are both obtained by solving a maximization problem.
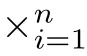
The principal’s goal is to design an incentive contract t(s)=(t(s),···,t(s)),which is a payment vector function proposed by the principal to the agents based on the observation of results which is denoted by s.Generally,it is assumed that the observed result s is a function of the agents’action pro file a and the exogenous random variable ξ∈Ξ,which is exogenously given.For example,the observable result s is related to the agents’actions a and the exogenous factor ξ in the following separate form:s(a,ξ)=k(a)+k(ξ)(see,e.g.,([12])).The set of all possible observed results is denoted by S.The probability distribution function and probability density function of the exogenous random variable ξ are P(ξ)and p(ξ),respectively.After the agents take action pro file a∈A,they need to pay a certain cost vector c(a),and the principal can get π(s(a,ξ))based on the observed result s(a,ξ).Suppose that the utility function π(s(a,ξ))is a strictly increasing concave function with respect to a.At this point,that means that the better the agents take the action pro file,the more the principal can obtain,and the marginal revenue will decrease.
Assume that both the principal and the agents are risk neutral.The expected pro fit of the principal is

The expected pro fit of agent i∈N is

The first kind of constraint for designing the optimal incentive mechanism is the incentivecompatibility constraint.The principal cannot observe the agents’action pro file a∈A,and in any incentive mechanism,the agent always chooses the action that maximizes his expected pro fit,so ifˉa is the agents’action pro file that maximizes their expected payoff,and a is the other action pro file that the agents can take,then the agents will only chooseˉa if they can get more expected pro fit when they takeˉa as opposed to when they take a.Therefore,the incentive-compatibility constraint is denoted by IC as follows:
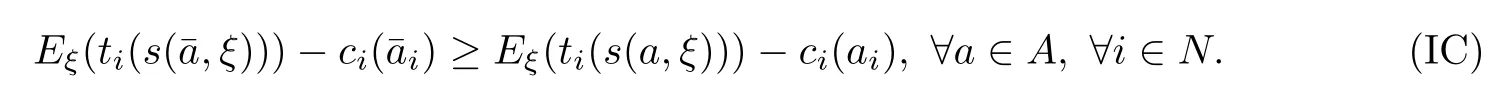
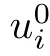
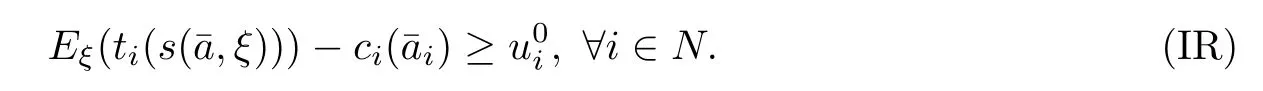
For the principal,his aim is to design a payment t(s)for all observed results s∈S and to maximize his expected pro fit.Thus,the optimal payment contract is the solution to the following optimization problem:
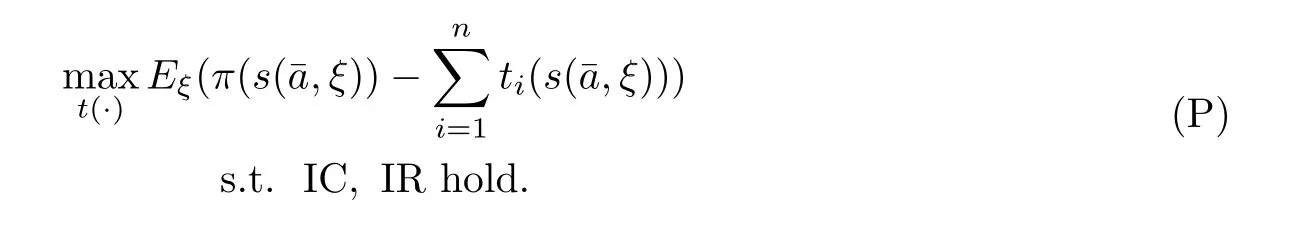
In this optimization problem,since the action pro file set A is an in finite point set,the numbers of constraints(IC)on the optimization problem(P)are in finite.In this paper,we assume that the principal knows the form of the payment function when designing the payment vector function,but the payment vector function contains some unknown parameters.For example,the principal designs a linear contract,i.e.,t(s)=α+βs.At this point,fi nding the optimal contract function t(s)is converted to a matter of finding its optimal parameters.In addition,ˉa is determined by the agent by maximizing his utility,and it also depends on the agent’s payment function.
4 The Optimal Incentive Mechanism
4.1 Semi-in finite Programming Model
We transform the incentive mechanism design problem(P)into the following optimization problem(P’):
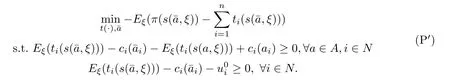
There are in finite number of constraints in the optimization problem(P),and we cannot use the Kuhn-Tucker theorem to solve this optimization problem.
It is assumed that the form of the incentive contract t(s)is known,but contains some unknown parameters.We denote all the variables that need to be decided as x=(x,···,x).As can be seen from the optimization problem(P),its general form is

where A is an in finite-point measurable set,and N is a finite-point set.This optimization problem is called a semi-in finite programming problem(SIP).
In the semi-in finite programming problem(SIP),the variable x∈Rrepresent the parameters in the payment vector function t,and there may be more than one unknown parameter.Therefore,after we use the algorithm of the semi-in finite programming problem to get the optimal solution to the optimization problem(P),we can find the optimal incentive mechanism for the incentive mechanism design problem(P).Thus,we need to design an algorithm for solving the semi-in finite programming problem(SIP) first.
4.2 M-penalty Function Method
Here,a kind of exterior penalty function method is proposed to solve the semi-in finite programming problem(SIP);this is called the M-penalty function method.The idea of designing this algorithm is derived from transforming the constrained programming problem into an unconstrained programming problem,and then obtaining the optimal solution to the constrained programming problem by solving this unconstrained programming problem.When designing an unconstrained programming problem,if the point is in the feasible domain of the original optimization problem,the objective function value will not be changed.If the point is not in the feasible domain,a penalty term is designed to punish the original objective function.This is an exterior penalty function method.
First,a constraint violation function for the semi-in finite programming problem(SIP)is constructed and denoted by G(x)as follows:

Obviously,G(x)=0 if and only if the constraints of the semi-in finite programming problem(SIP)are satis fied.G(x)>0 if and only if the point x∈Rdoes not satisfy the constraints of the semi-in finite programming problem(SIP).
We de fine the penalty function as

where σ>0 is the penalty factor.
We denote x(σ)as a solution to the following optimization problem:

The relationship between the optimal solution to the optimization problem(PG)and the optimal solution to the original semi-in finite programming problem(SIP)is illustrated in the following Lemma:
Lemma 4.1
If x(σ)is the optimal solution to an optimization problem(PG)and G(x(σ))=0,that is,if x(σ)satis fies the constraints of the semi-in finite programming problem(SIP),then x(σ)is the optimal solution to the semi-in finite programming problem(SIP).Proof
Since x(σ)is the optimal solution to the optimization problem(PG),then?x∈R,
Since x(σ)satis fies the constraints of the semi-in finite programming problem(SIP)such that G(x(σ))=0,for any point x that satis fies the constraints of the semi-in finite programming problem(SIP),we have

Then x(σ)is also the optimal solution for the semi-in finite programming problem(SIP).Therefore,the conclusion is established.
Lemma 4.1 shows that finding the optimal solution to the semi-in finite programming problem(SIP)can be transformed into solving the optimization problem(PG).Based on this idea,we design the M-penalty function method to solve the semi-in finite programming problem(SIP)as follows:
M-penalty function method
(1)Step 1:Given an initial point x,take σ>0,M>1,ε>0.k:=1.
(2)Step 2:Using the initial point value xto solve the optimization problem(PG)when σ=σ,obtain x(σ).Let x=x(σ).
(3)Step 3:If

then stop,and the optimal solution is x.Otherwise,let σ:=Mσ,k:=k+1,and go to the Step 2.
Here ε is called the error factor and M is called the ampli fication factor.
5 Convergence Analysis

Since M>1 and σ>0,it can be seen from the equation(5.5)that G(x)≤G(x)holds.
According to equation(5.3)and equation(5.1),we have

Then,based on equation(5.6),we know that f(x)≥f(x)holds.Therefore,the conclusion is established.
As can be seen from Lemma 5.1,the value of the objective function corresponding to the sequence of points generated by the M-penalty function method decreases gradually.
Lemma 5.2
Let x(σ)be the optimal solution to optimization problem(PG),and let δ=G(x(σ)).Then x(σ)is also the optimal solution to the constrained optimization problem
Proof
For any x that satis fies equation(5.8),we have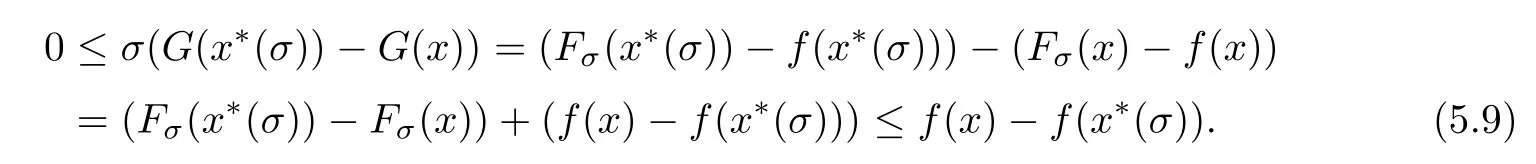
According to equation(5.9),for any x that satis fies equation(5.8),we have

Therefore,x(σ)is also the optimal solution to the constrained optimization problem(5.7)–(5.8).The conclusion is established.

Through Lemma 5.1 and Lemma 5.2,we can get the convergence theorem of the M-penalty function method.
Theorem 5.3
Assume that the error factor ε in the M-penalty function method satis fies the condition that
Then,the algorithm must be terminated within finite iterations.


As can be seen from equation(5.11),there isˉx such that



As shown by equation(5.2),we have

Let σ→+∞.Then

This conclusion contradicts equation(5.14).Therefore,Theorem 5.3 is true,and the conclusion is established.
According to Theorem 5.3,if the semi-in finite programming problem(SIP)has a feasible solution,for any given ε>0,the M-penalty function method will be terminated at the optimal solution to the optimization problem(5.7)–(5.8)and δ≤ε.
If the algorithm cannot be terminated within finite iterations,we have the following conclusions:
Theorem 5.4
If the M-penalty function method will not be terminated within finite iterations,then for any error factor ε,we have
and




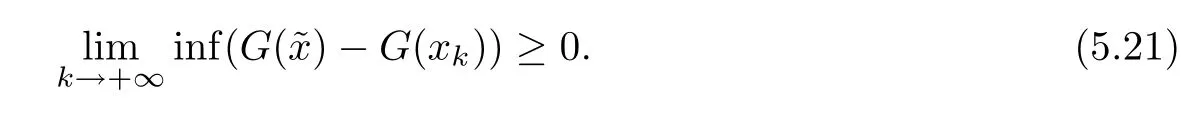
Therefore,the equation(5.18)is established.


and the constraint condition(5.20)is satis fied.Therefore,we have

It can be seen from Lemma 5.1 that f(x)monotonically approaches to f(x).Therefore,it can be known from equation(5.22)that,for any sufficiently large k,

It can be known from equation(5.23)and equation(5.24)that
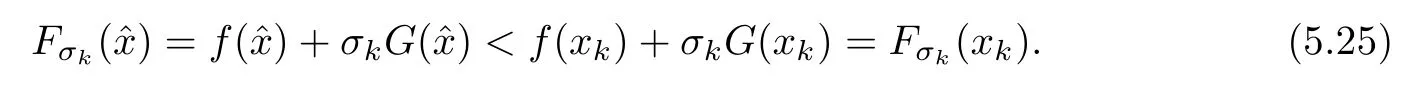

From the above two theorems,the following corollary can be directly obtained:


Then,we have


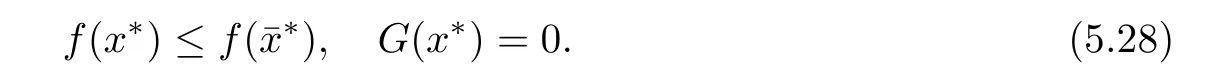


6 Numerical Example

The expected pro fit of the agent is
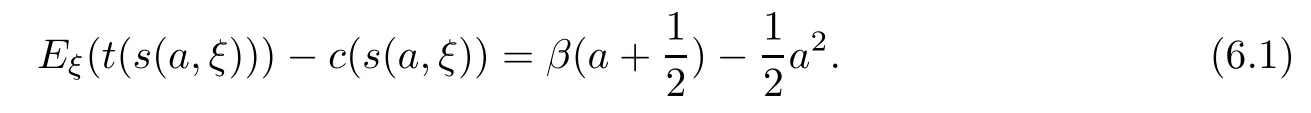


Assuming that the agent’s disagreement pro fit uis 0,the optimal incentive mechanism for this principal-agent problem is the solution to the following semi-in finite programming problem:

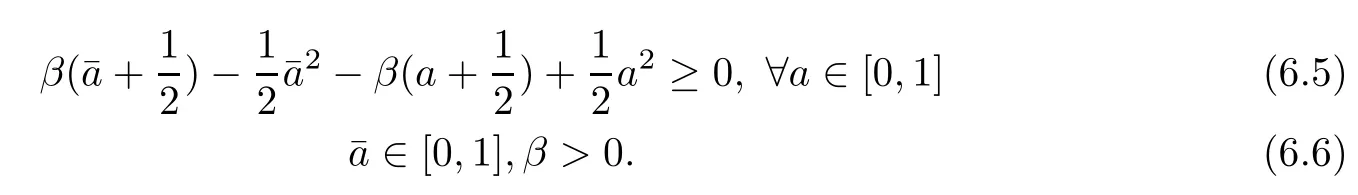
Next,we use the M-penalty function method in Section 4 to solve the semi-in finite programming problem(6.3)–(6.6).
The constraint violation function is
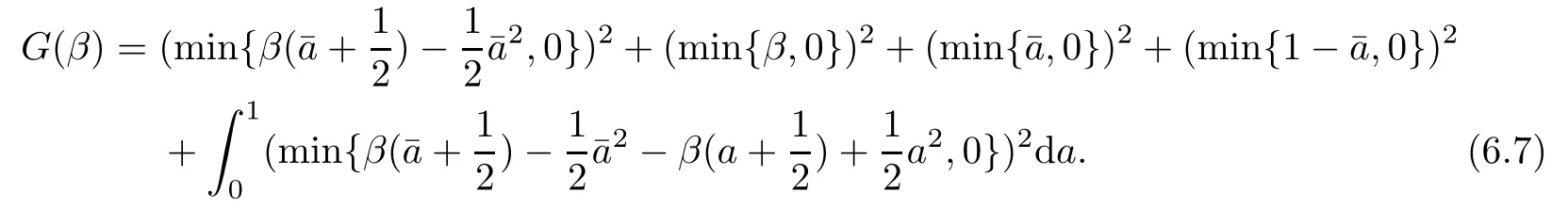
The optimization problem(PG)is

Since this is a standard linear contract,we can use traditional method(e.g.,in[11,12])to verify this result.
First,we modify the equation(6.1),and we get


7 Conclusions
This paper mainly designs an iterative algorithm to find the optimal incentive mechanism for the principal-agent problem under moral hazard where the number of agent action profi les is in finite,and where there are an in finite number of results that can be observed by the principal.The main characteristic of this principal-agent problem is that the number of constraints is in finite.Given the form of payment vector function designed by the principal,the principal-agent problem can be transformed into a semi-in finite programming problem.A exterior penalty function method(called the M-penalty function method)for solving semi-in finite programming problems is proposed,and its convergence is illustrated.By using the M-penalty function method designed in this paper,we can obtain the optimal incentive mechanism for the principal-agent problem with an in finite number of incentive-compatibility constraints under moral hazard.
In this paper,the in finite number of constraints are mainly caused by the in finite number of agent action pro files.In addition,if the set of agents is assumed to be continuous,the number of individual rational constraints will be in finite,which will also make the incentive mechanism design problem a semi-in finite programming problem.At this point,the M-penalty function method designed in this paper for solving semi-in finite programming problems is also applicable for solving the incentive mechanism design problem.
It should be noted that in this paper,we assume that the form of the principal’s payment function to the agent is given,but it contains some uncertain parameters.The optimal solution to the semi-in finite programming problem are the optimal parameters of the payofffunction to the incentive mechanism design problem.In a more general case,the form of the payment function may not be known.Therefore,the incentive mechanism design problem is a variational problem with an in finite number of constraints.Compared with the algorithm for solving semiin finite programming problems,the method for solving this problem is more complex.
Acknowledgements
We would like to express our gratitude to all those who helped us during the writing and revising of this paper.In particular,we are very grateful to the two anonymous reviewers for their comments,which were of great signi ficance. Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- THE UNIQUENESS OF THE LpMINKOWSKI PROBLEM FOR q-TORSIONAL RIGIDITY?
- HYERS–ULAM STABILITY OF SECOND-ORDER LINEAR DYNAMIC EQUATIONS ON TIME SCALES?
- ON NONCOERCIVE(p,q)-EQUATIONS?
- THE CONVERGENCE OF NONHOMOGENEOUS MARKOV CHAINS IN GENERAL STATE SPACES BY THE COUPLING METHOD?
- POSITIVE SOLUTIONS OF A NONLOCAL AND NONVARIATIONAL ELLIPTIC PROBLEM?
- THE INITIAL BOUNDARY VALUE PROBLEMS FOR A NONLINEAR INTEGRABLE EQUATION WITH 3×3 LAX PAIR ON THE FINITE INTERVAL?
