HYERS–ULAM STABILITY OF SECOND-ORDER LINEAR DYNAMIC EQUATIONS ON TIME SCALES?
Douglas R.ANDERSON
Department of Mathematics,Concordia College,Moorhead,MN 56562 USA
E-mail:andersod@cord.edu
Masakazu ONITSUKA
Department of Applied Mathematics,kayama University of Science,Okayama,700-0005,Japan
E-mail:onitsuka@xmath.ous.ac.jp
Abstract We investigate the Hyers–Ulam stability(HUS)of certain second-order linear constant coefficient dynamic equations on time scales,building on recent results for firstorder constant coefficient time-scale equations.In particular,for the case where the roots of the characteristic equation are non-zero real numbers that are positively regressive on the time scale,we establish that the best HUS constant in this case is the reciprocal of the absolute product of these two roots.Conditions for instability are also given.
Key words stability;second order;Hyers–Ulam;time scales
1 Introduction
The story of Ulam and Hyers–Ulam stability(HUS)is recounted in many papers dealing with the subject,as has the development of dynamic equations on time scales.In this work,we continue the connection between those two areas by extending recent results on HUS for first-order time scale equations with constant coefficient[1],to second-order dynamic equations with constant coefficients.Other papers exploring HUS for dynamic equations on time scales include[2–6].With a more general view,[7]established Ulam–type stability for a first-order equation using measure theory.
First,a brief review of time scales.Any closed,nonempty subset of the real line R is a time scale[11].For example,R,hZ,and N are common examples of time scales.In this paper,we denote a time scale by T.We de fine the jump operators σ,ρ:T→T by
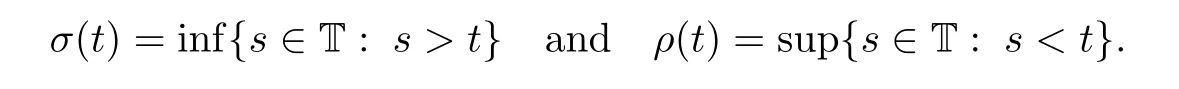
Setμ(t)=σ(t)?t.The point t∈T is called right-scattered,right-dense,left-dense,leftscattered if σ(t)>t,σ(t)=t,ρ(t)=t,ρ(t)
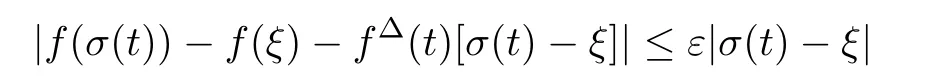
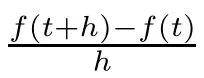
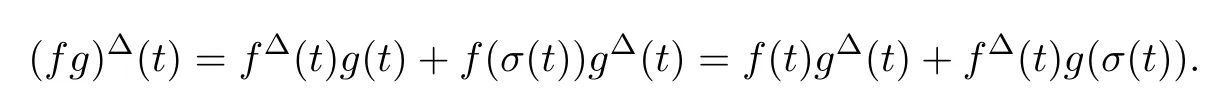
In this study,we call it the?-derivative product rule.
Initially,we focus on the first-order linear dynamic equation


Theorem 1.1
([1,Theorem 3.7]) Let t∈T and ε>0 be given.Suppose a function φ:T→R that is delta-differentiable on Tsatis fies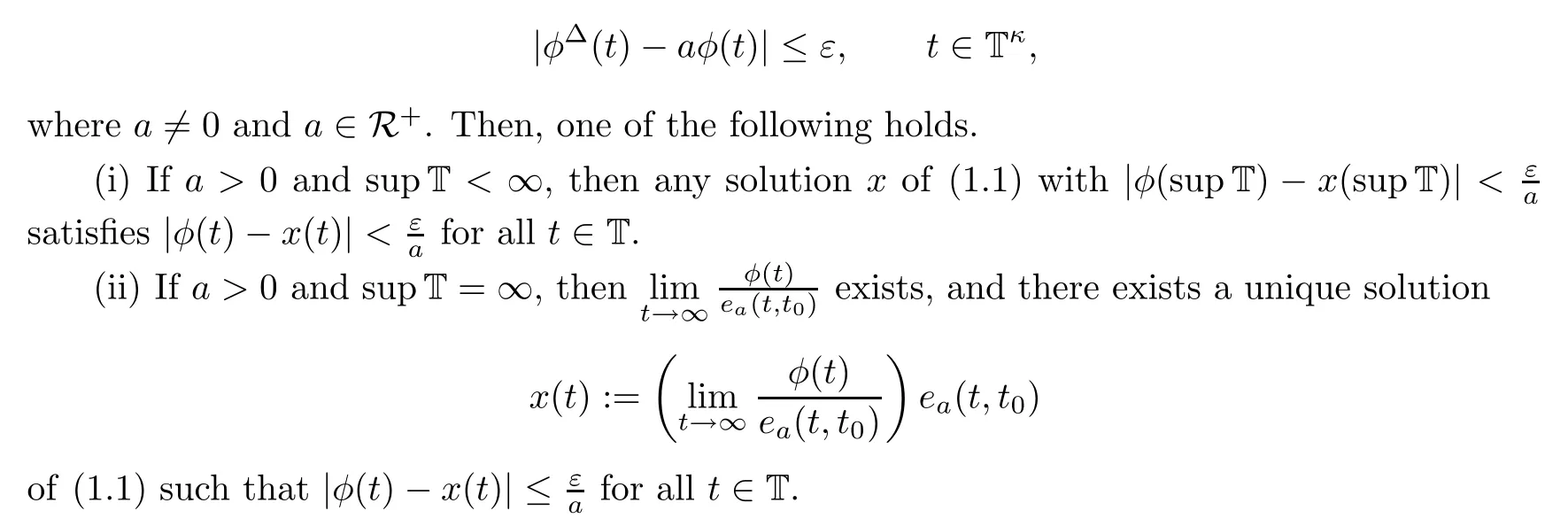
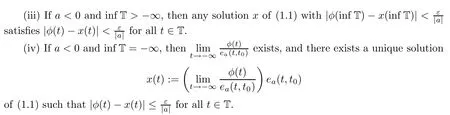
Remark 1.2
Since T is any closed,nonempty subset of R,we have the following facts:supT<∞if and only if maxT exists,and thus,supT=maxT holds;supT=∞if and only if maxT does not exist;inf T>?∞if and only if minT exists,and thus,inf T=minT holds;inf T=?∞if and only if minT does not exist.2 First-order Non-homogeneous Linear Dynamic Equations
A function f:T→R is said to be rd-continuous if it is continuous at all right-dense points in T and its left-sided limit exists(fi nite)at left-dense points of T.If f is rd-continuous,then there is a function F such that F=f(see,[11]).We de fine
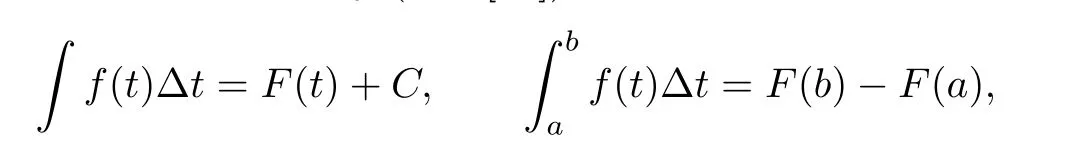
where C is an arbitrary constant of integration.Next,consider the first-order non-homogeneous linear dynamic equation

where the function f is rd-continuous on T.Theorem 1.1 is improved as follows.
Theorem 2.1
Let t∈T and ε>0 be given.Suppose a function φ:T→R that is delta-differentiable on Tsatis fies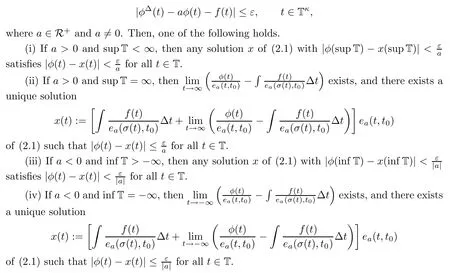
Before proving the theorem,we give two lemmas as follows.
Lemma 2.2
([11,Theorem 6.2]) Let t∈T.If a∈R,then the inequality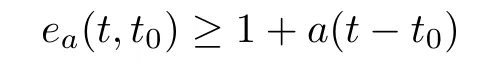
holds for all t∈[t,∞).
Lemma 2.3
([1,Lemma 3.5]) Let t∈T.If a∈Rand a<0,then the inequality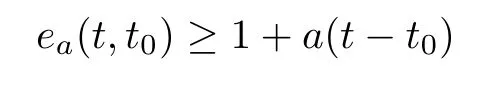
holds for all t∈(?∞,t].
Proof of Theorem 2.1
Given any ε>0,let φ:T→R satisfy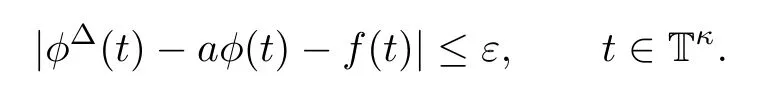
Fix t∈T,and let
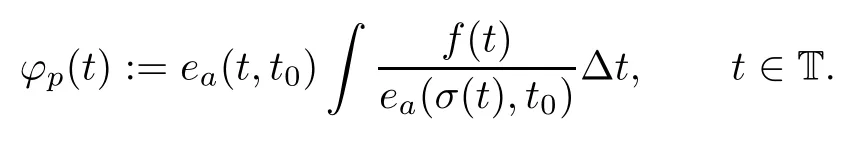
Then,?is a particular solution of(2.1).We see,moreover,that
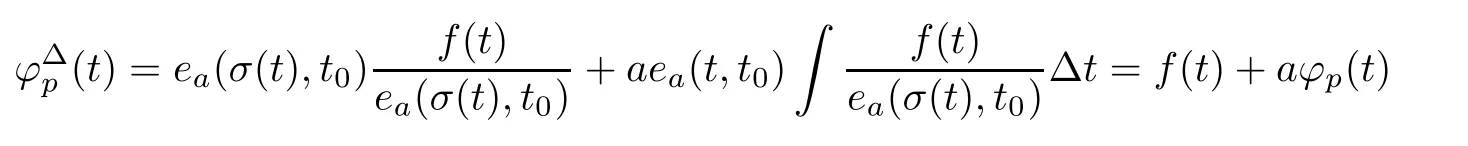
follows from the?-derivative product rule.Let y(t)=φ(t)??(t).Then,
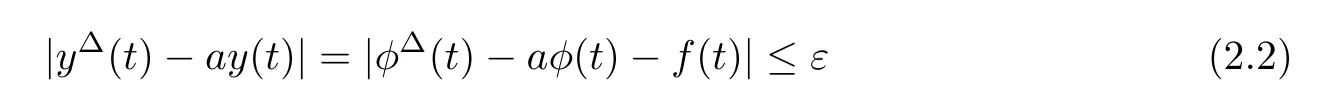
holds for all t∈T.
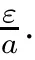
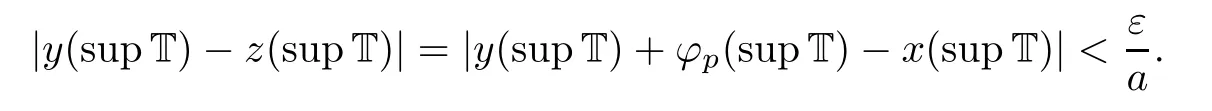
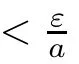

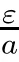
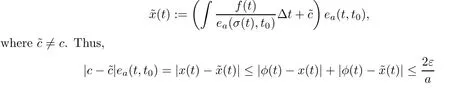
for all t∈T.This is a contradiction of the fact that e(t,t)→∞as t→∞by Lemma 2.2.
The arguments given above for(i)and(ii)can be modi fied to establish the validity of(iii)and(iv);the details are omitted.Note here that the uniqueness of the solution x in(iv)is shown by using Lemma 2.3.This completes the proof.
In a de finition analogous to that given for the homogeneous equation(1.1),equation(2.1)is Hyers–Ulam stable(HUS)on T if and only if there exists a constant K>0 satisfying the following property.For any ε>0,if some function φ:T→R satis fies|φ(t)?aφ(t)?f(t)|≤ε for all t∈T,then there exists some solution x:T→R of(2.1)such that|φ(t)?x(t)|≤Kε for all t∈T.By Theorem 2.1,we get a simple result,immediately.

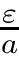
For the cases a<0 with inf T>?∞or inf T=?∞,we can use Theorem 2.1(iii)and(iv),so that,(2.1)has HUS on T when a<0 as well.

Proof
Let t∈T.For arbitrary ε>0,let φ:T→R be given by

Corollary 2.4 and Theorem 2.5 imply the following theorem,immediately.

Remark 2.7
Almost at the same time as the start of this study,Shen and Li[12]gave a result similar to Theorem 2.1.The difference from their result is that the integral that appears in Theorem 2.1 is the inde finite integral.Therefore,our result is represented by any primitive function.Furthermore,in this study,we deal with the best(minimum)value of the HU-stability constant.Shen and Li[12]do not study the minimum HUS constant for(2.1)on T.For this reason,the originality of this section is guaranteed.If we can obtain the minimum HUS constant,then it is often called the best HUS constant or the best constant.For the best constant for functional equations and some positive linear operators,see Popa and Ra?sa[13,14].For linear differential equations and linear difference equations,the papers[15–18]are representative of recent results.3 Second-Order Linear Dynamic Equations
Using the previous results on first-order linear dynamic equations,in this section we focus on the second-order linear constant coefficient dynamic equation
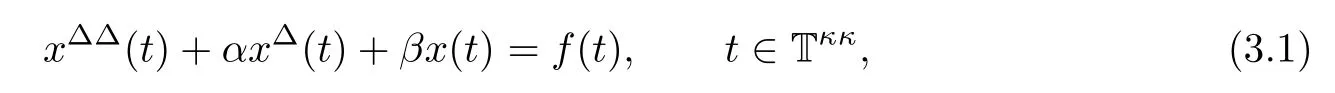
where α and β are real numbers and f:T→R is rd-continuous.Here,the set Tis de fined by T=T?{M,M}if T and Thave left-scattered maximums M and M,respectively;T=Tif T has a left-scattered maximum M,but Tdoes not have a left-scattered maximum;T=T if T does not have a left-scattered maximum.Note here that if T does not have a left-scattered maximum,then T=T,so that,Tdoes not have a left-scattered maximum.We say that(3.1)is Hyers–Ulam stable(HUS)on T if and only if there exists some constant K>0 with the following property.For arbitrary ε>0,if some function φ:T→R satis fies
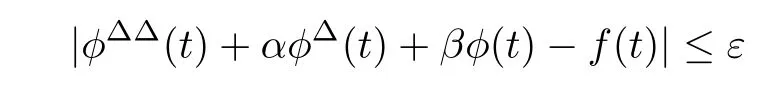
for all t∈T,then there exists some solution x:T→R of(3.1)such that|φ(t)?x(t)|≤Kε for all t∈T.Any such constant K is called an HUS constant for(3.1)on T.Hyers–Ulam stability for second-order linear constant coefficient difference equations,differential equations,and dynamic equations on times scales were studied in[19–26].In addition,Hyers–Ulam stability for second-order non-constant coefficient differential equations,functional differential equations,and dynamic equations were discussed in[27–31].The first result for(3.1)is as follows.
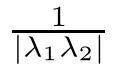
Proof
Set ψ(t):=φ(t)?λφ(t)for t∈T.Since φand φ are delta-differentiable,we get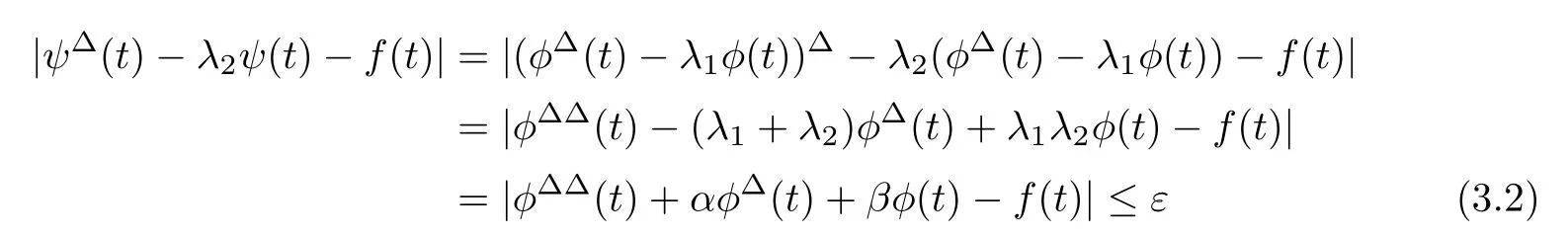
for all t∈T.Using Corollary 2.4 with(3.2),a solution y:T→R of

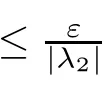
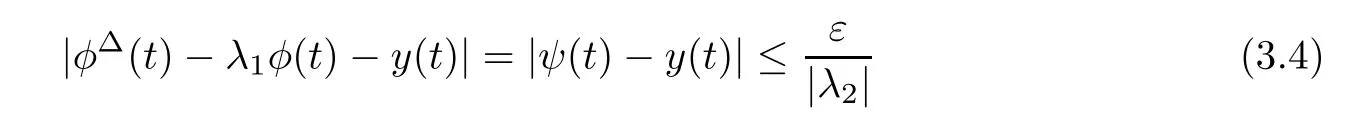
for all t∈T.Since y is a solution of(3.3),y is delta-differentiable,and thus y is rd-continuous on T.Using Corollary 2.4 with(3.4),a solution x:T→R of

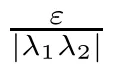
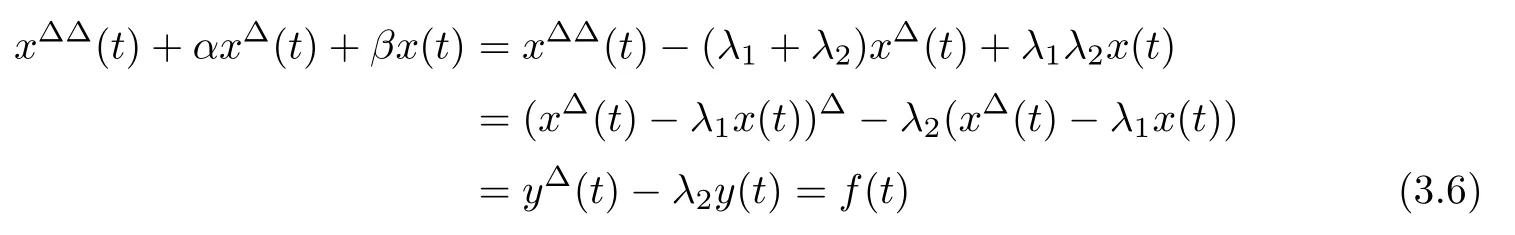
for t∈T.This completes the proof.
Theorem 3.2
Suppose that supT=∞and inf T=?∞,and that the characteristic equation λ+αλ+β=0 for(3.1)has non-zero real roots λand λwith λ,λ∈R.Let t∈T and ε>0 be given.If a twice?-differentiable function φ:T→R satis fies

so that the assertion is established.Next,consider the case λ=λ.By[11,Theorem 2.36],it is known that
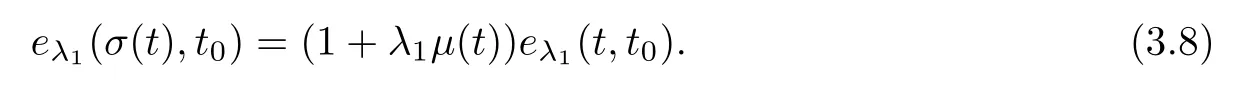
Using this,the assertion is true.
From[11,Theorems 3.16 and 3.34]the following lemma is immediately true.
Lemma 3.4
For(3.1),assume the characteristic equation λ+αλ+β=0 has non-zero real roots λand λwith λ,λ∈R.Let t∈T.Then,the general solution of(3.1)is given by: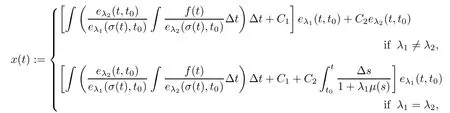
where Cand Care arbitrary constants.
Lemma 3.5
([1,Lemma 5.2]) Assume a∈Rwith a<0,and let t∈T.Then,the inequality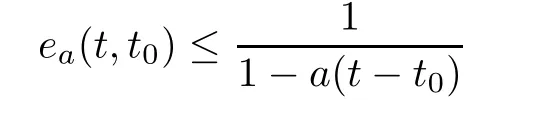
holds for all t∈[t,∞).
Lemma 3.6
Assume a>0,and let t∈T.Then,the inequality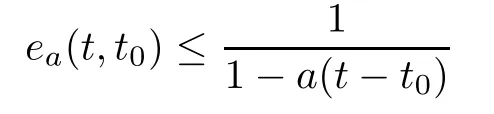
holds for all t∈(?∞,t].
Proof
Let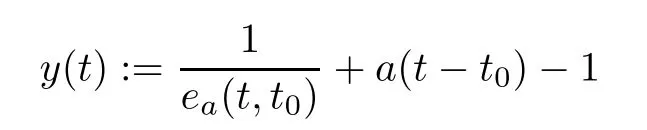
for all t∈(?∞,t],then y(t)=0.We will show that y(t)≥0 for all t∈(?∞,t].Using the?-derivative quotient rule,we have
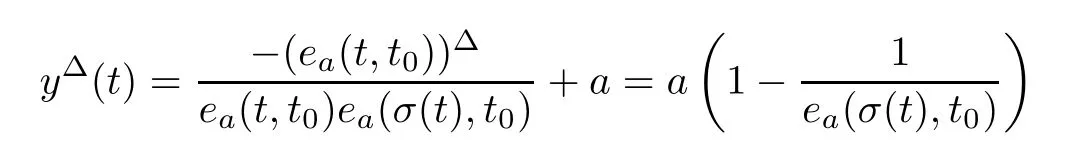
for all t∈(?∞,t).Note here that t≤σ(t)≤tfrom t
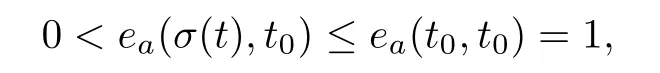
and thus,y(t)≤0 for all t∈(?∞,t).Consequently,we obtain y(t)≥0 for all t∈(?∞,t],completing the proof.
Lemmas 2.2,2.3,3.5 and 3.6 imply the following lemma.

(i)If supT=∞,then
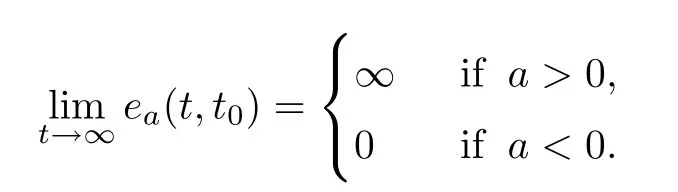
(ii)If inf T=?∞,then
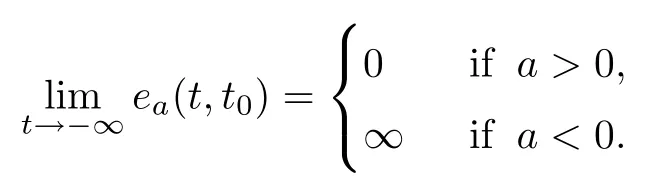

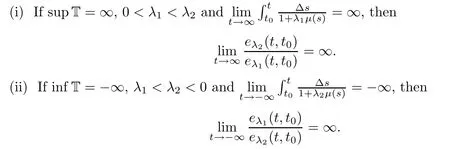
Proof
First,we consider case(i).By(3.7),(3.8)and λ,λ∈R,we have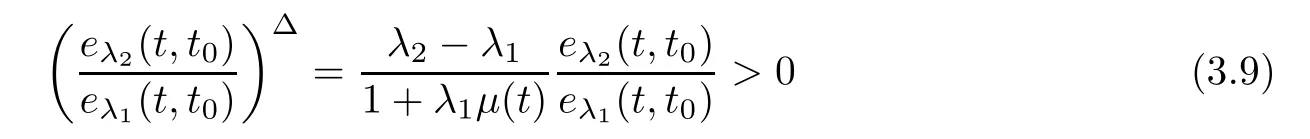
for all t∈T.Using this inequality,we get
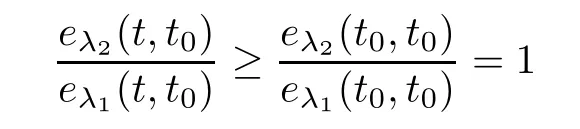
for all t∈[t,∞).This together with(3.9)implies that
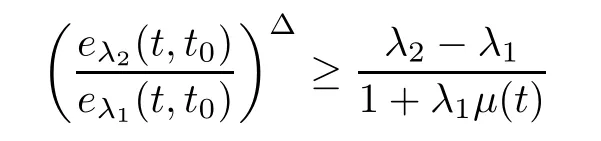
for all t∈[t,∞),and thus,
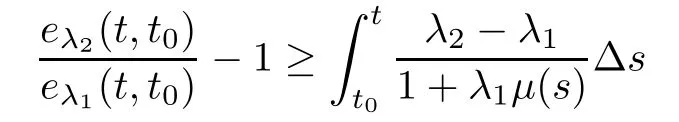
for all t∈[t,∞).Therefore,we get
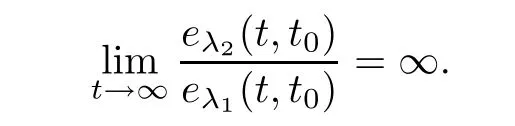
Next,we consider case(ii).In the same way,we have
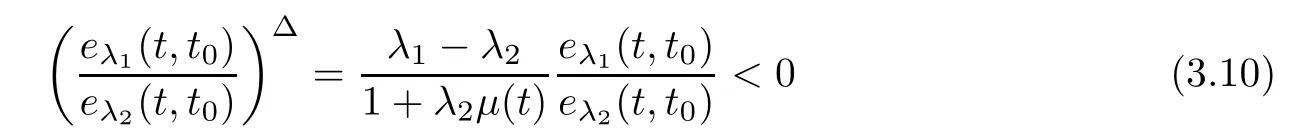
for all t∈T.From this,we get
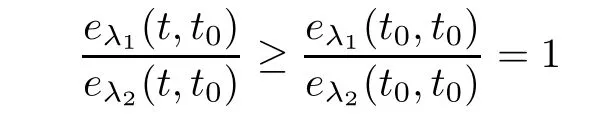
for all t∈(?∞,t].This together with(3.10)implies that
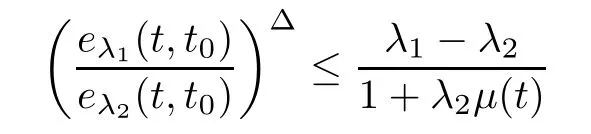
for all t∈(?∞,t],and thus,

for all t∈(?∞,t].Therefore,we get
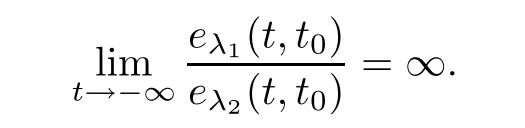
Remark 3.9
Let λ∈R.If T=R and t=0,thenμ(t)=0,so that we have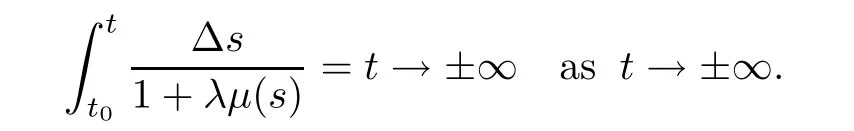
If T=hZ and t=0,thenμ(t)=h,so that we have
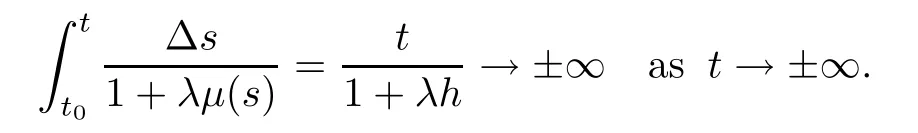
From these facts,we say that the assumptions
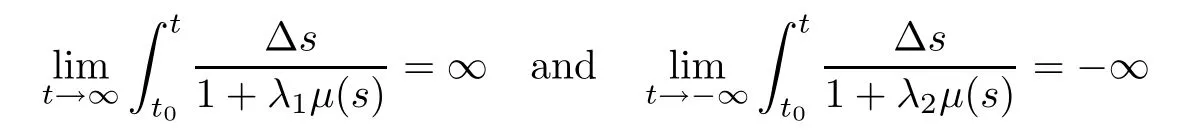
in Theorem 3.2 and Lemma 3.8 are natural conditions.
Proof of Theorem 3.2
Set ψ(t):=φ(t)?λφ(t)for t∈T.Then,we get(3.2)for all t∈T.
from Lemma 3.3,where C is an arbitrary constant.
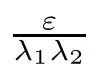

from Lemma 3.3,where C is any constant,and F is de fined by(3.11).
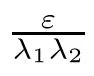


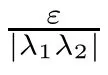
To end this section,we give instability results for the homogeneous version of(3.1),under certain assumptions on the characteristic roots and their corresponding dynamic exponential functions.
Theorem 3.10
Assume supT=∞.The second-order homogeneous dynamic equation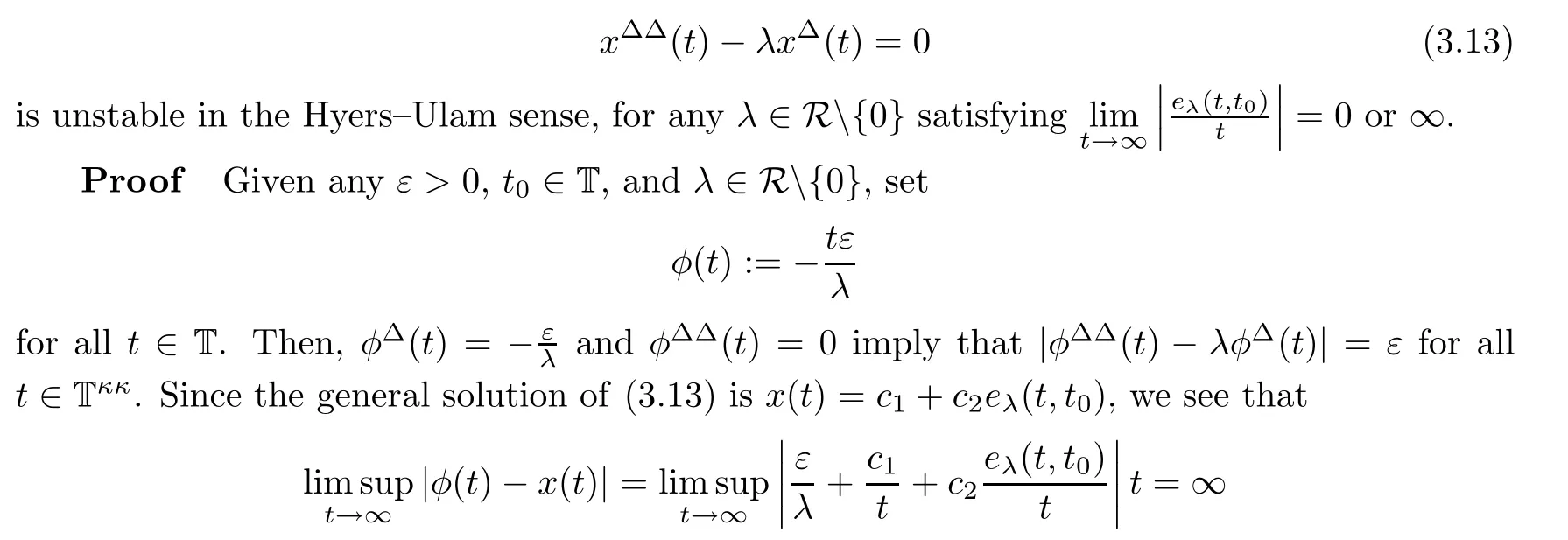
for any choice of cand c.This ends the proof.
Theorem 3.11
Assume supT=∞,and fix t∈T.If λ∈R but not positively regressive,with m≤|e(t,t)|≤M for all t∈T,for some 0

4 Minimum HUS Constant


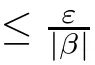
From Remark 3.9,we get the following corollaries.
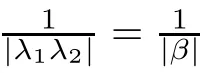
Remark 4.3
In[17],Baias and Popa studied the Hyers–Ulam stability of the second order linear differential operator.When restricted to the case where the characteristic equation has non-zero real roots,a result given in[17]matches Corollary 4.2.Note that they are also considering the case of complex roots.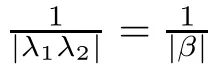
Remark 4.5
When T=hZ,the condition λ,λ∈Rmeans that 1+λh>0 and 1+λh>0.Since λand λare non-zero real roots of(3.1),we have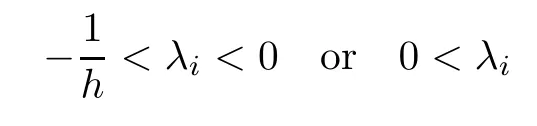
for i∈{1,2}.Under this condition,using a result in[18],we can obtain the same best HUS constant given in Corollary 4.4.
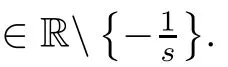

5 Conclusion and Future Direction
This study deals with conditions under which second-order linear dynamic equations on time scales with constant coefficients are Hyers–Ulam stable(HUS),but also unstable in other cases.To achieve this goal,HUS for first-order non-homogeneous linear dynamic equations is established first.Moreover,the best HUS constant is obtained in some cases.By using the results,a sufficient condition for HUS and the main theorem related to HUS are obtained.It is also shown that an HUS constant obtained here is the best one.Finally,the results for several time scales are introduced.
The stability results presented here cover only the case where the characteristic equation has non-zero real roots,with instability in the zero-root case,because these results depend on the results of the first-order dynamic equation.If one can obtain HUS results for the complexvalued dynamic equations of first-order,one will obtain some results for the case where the characteristic equation has complex roots,by using the same methods.
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- THE UNIQUENESS OF THE LpMINKOWSKI PROBLEM FOR q-TORSIONAL RIGIDITY?
- ON NONCOERCIVE(p,q)-EQUATIONS?
- THE CONVERGENCE OF NONHOMOGENEOUS MARKOV CHAINS IN GENERAL STATE SPACES BY THE COUPLING METHOD?
- POSITIVE SOLUTIONS OF A NONLOCAL AND NONVARIATIONAL ELLIPTIC PROBLEM?
- A PENALTY FUNCTION METHOD FOR THE PRINCIPAL-AGENT PROBLEM WITH AN INFINITE NUMBER OF INCENTIVE-COMPATIBILITY CONSTRAINTS UNDER MORAL HAZARD?
- THE INITIAL BOUNDARY VALUE PROBLEMS FOR A NONLINEAR INTEGRABLE EQUATION WITH 3×3 LAX PAIR ON THE FINITE INTERVAL?
