POSITIVE SOLUTIONS OF A NONLOCAL AND NONVARIATIONAL ELLIPTIC PROBLEM?
Lingjun LIU(劉玲君)
Institute of Applied Mathematics,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China
E-mail:liulingjun@amss.ac.cn
Feilin SHI(石飛林)?
School of Mathematics and Statistics,Hunan Normal University,Changsha 410081,China
E-mail:shifeilin1116@163.com
Abstract In this paper,we will study the nonlocal and nonvariational elliptic problemwhere a>0,α>0,1 Key words positive solutions;nonvariational elliptic problem;a priori estimates Let ? be an open bounded smooth domain with a boundary?? in R(N≥2).We consider the following nonlocal and nonvariational elliptic problem: Nonlocal problems like problem(1.1)arise in several physical and biological situations,and are a generalization of the problem For the case q=1,the equation in problem(1.2)can be traced back to 1992 as a biological model in[8],where u described the density of bacteria.Chipot-Lovat also investigated the relevant nonlocal elliptic and parabolic problems in[6,7].In the case q=2,we have the well-known Carrier’s equation as a model of the vibration of a nonlinear elastic string. In recent years,nonlocal problems such as the famous Kirchhoffequations have attracted much attention;see[1,4,5,16–18,20–23]for some of the main contributions.As is widely known,the variational method is one of the most common ways to study the existence of solutions,since these equations always have a variational structure.Unfortunately,problems(1.1)and(1.2)do not possess a variational structure.The problem(1.2)has been studied by a few authors.In 2004,Corr?ea[9]used the comparison principle and a fixed point theorem to establish the existence of solutions to problem(1.2)with the more general function a depending on the variable x.In 2010,Corr?ea and Figueiredo[10]applied a variational approach to prove the existence of solutions to problem(1.2).Moreover,there are techniques that exploit variational methods in non-variational problems for a Laplacian operator with an odd and periodic nonlinearity([2]).It is worth mentioning that the methods in[2,9,10]can not be directly applied to the problem(1.1). When h(x,u,?u)≡0 and a=0,problem(1.1)is reduced to the following classical semilinear elliptic equation: Before formulating the main result of the present paper,we first consider the case of h(x,u,?u)≡0.We analyse the solvability of the following problem: Theorem 1.31 Introduction

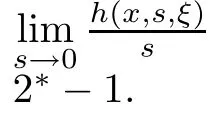
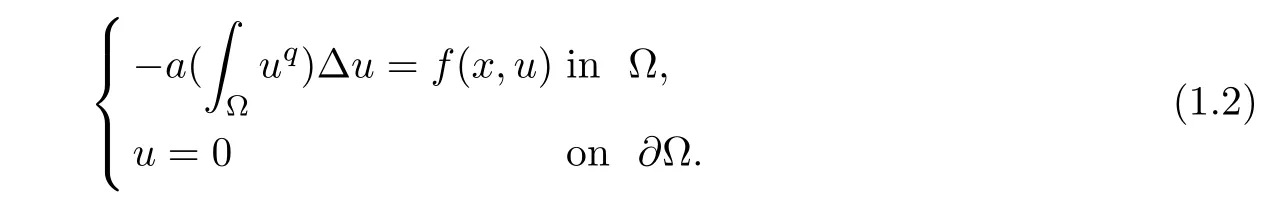


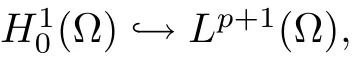

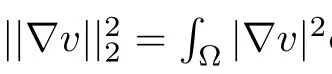
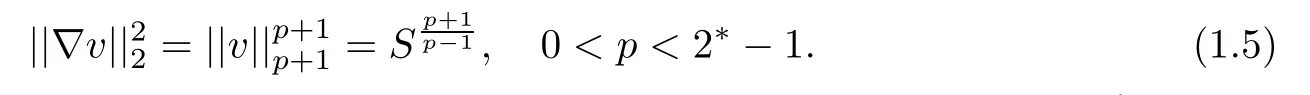

Theorem 1.4
Assume that α>0,a>0,12 The Proof of Theorem 1.1,Theorem 1.2 and Theorem 1.3
In this section,we give the proof of Theorem 1.1 by making use of the solution v of problem(1.3).Our arguments are inspired by the ideas in[12].
Proof of Theorem 1.1
Based on the given conditions,we analyse the solvability of problem(1.6).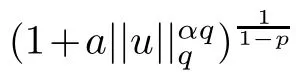
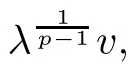

Now,for the purpose of getting the existence of u,we only need to discuss the existence and related properties of positive solutions for equation(2.1).
Let
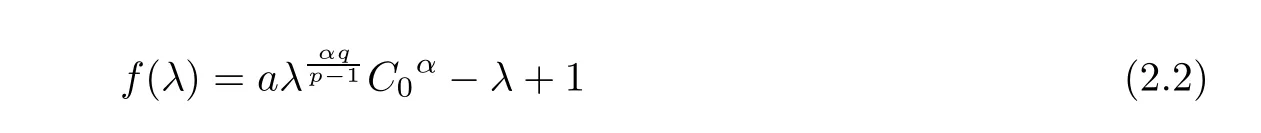
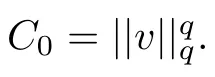
We consider the existence and multiplicity of positive solutions for f(λ)=0.
It is easy to see for any λ>0 that
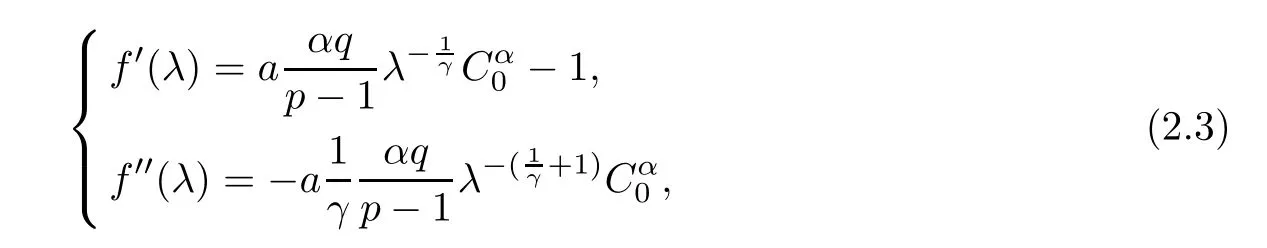
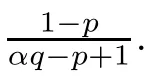
Then,we have the following:
(1)If 0 Hence,the equation f(λ)=0 has a unique solution in(0,+∞).This implies that the problem(1.6)has as many solutions as problem(1.3). From this,we get From the relationship between u and v we can see that the number of solutions for problem(1.6)is related to λ,and(ii)is proved. We have We can conclude from(2.6)that the equation f(λ)=0 has exactly one solution in(0,+∞). (4)If p=αq+1,we can obtain To conclude,from(1)and(3)we obtain(i)of Theorem 1.1.From(2)and(4)we deduce(ii)and(iii),respectively. In this section,we obtain a priori estimates for the solutions of problem(1.1).For simplicity,we consider the following problem: For any bounded smooth domain ??R,we let λ(?)be the first Dirichlet eigenvalue of the Laplacian,that is, We also denote that where we have the positive constant b∈(1,2). To get the bound of positive solutions for problem(3.1),we need the following well known Liouville Theorem for a semilinear problem: Lemma 3.1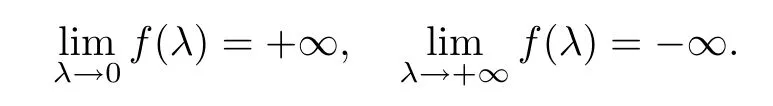
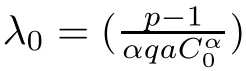
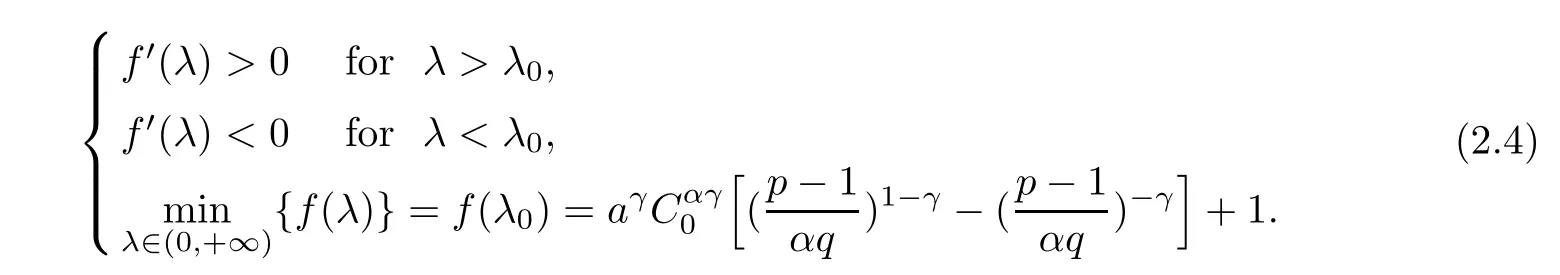
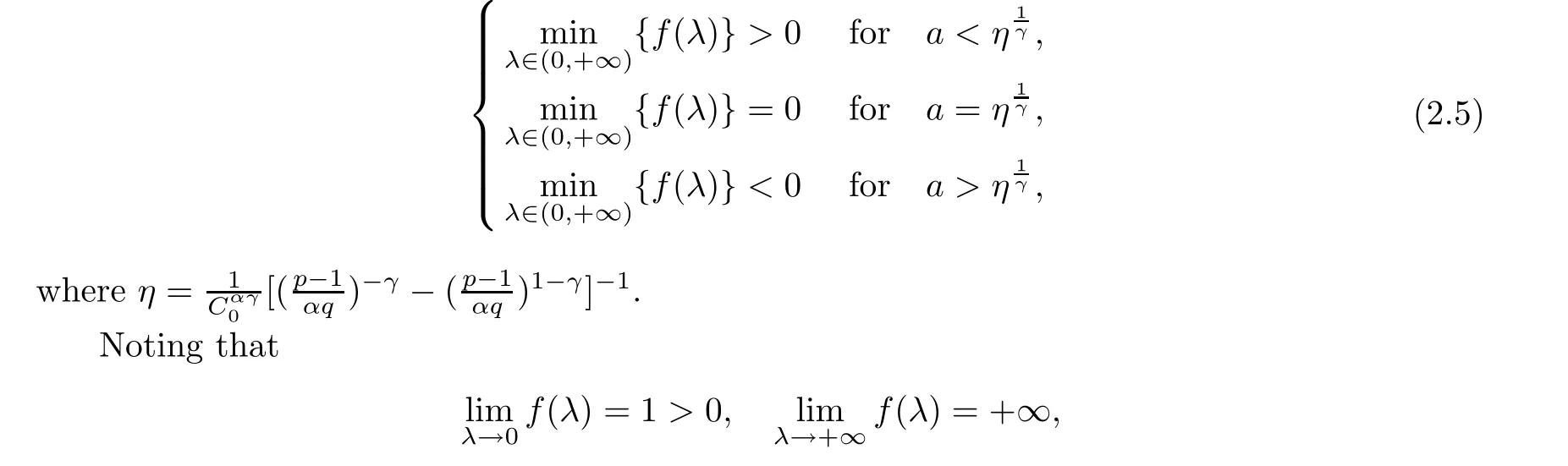
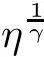
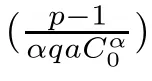
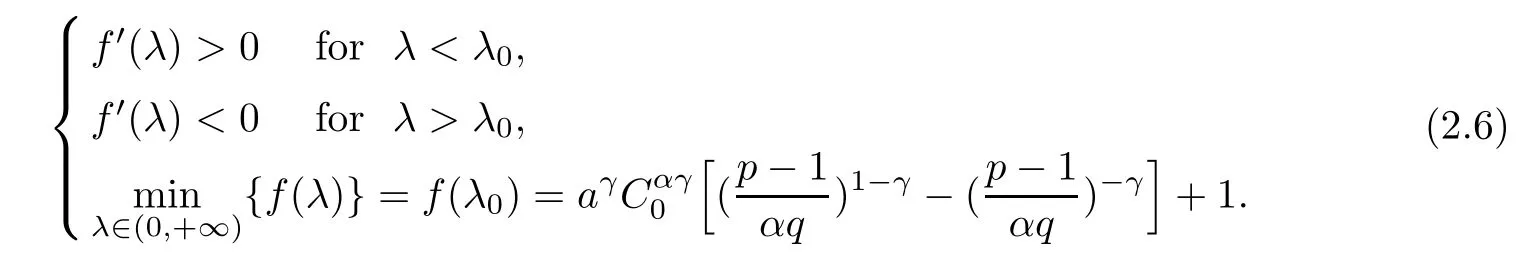
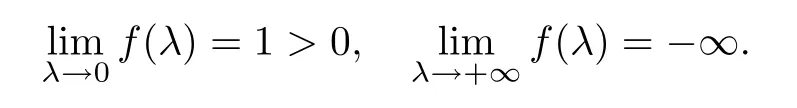
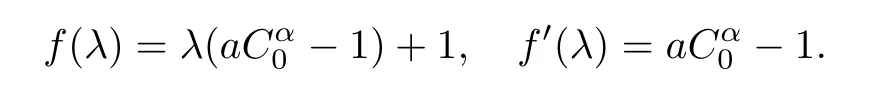
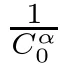
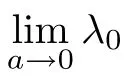
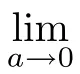
3 A Priori Estimates

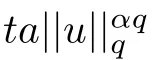
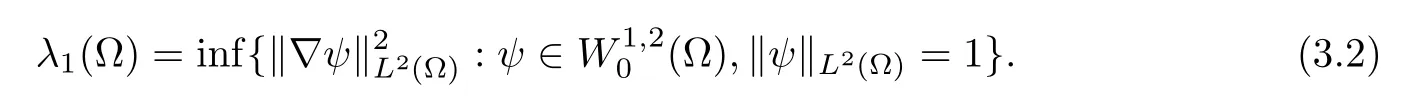

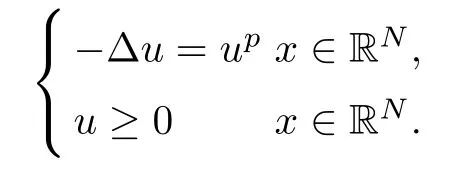
Lemma 3.2
([19]) If 1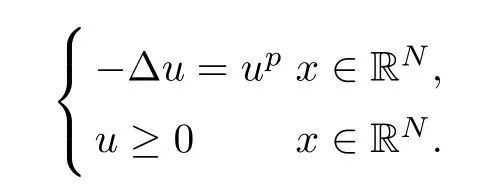
Lemma 3.3
([19]) If 1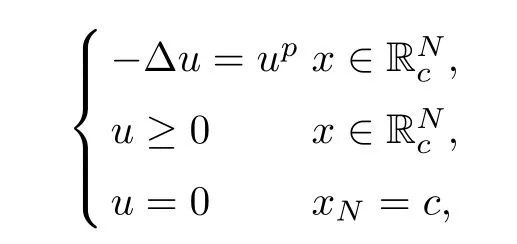
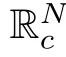
Lemma 3.4
([12]) If 0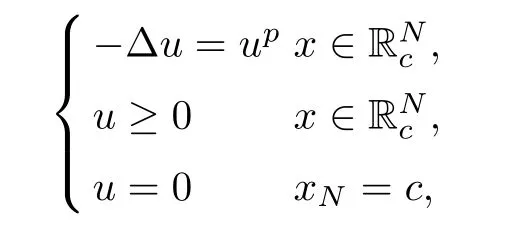
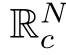
We denote by||·||the essential supremum norm.Then one of the main results in this section can be stated as follows:
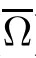
Proof
We divide the proof into the following two steps:Step 1
The bound from above u.Multiplying the differential equation in problem(3.1)by u and integrating the resulting equation on ?,we obtain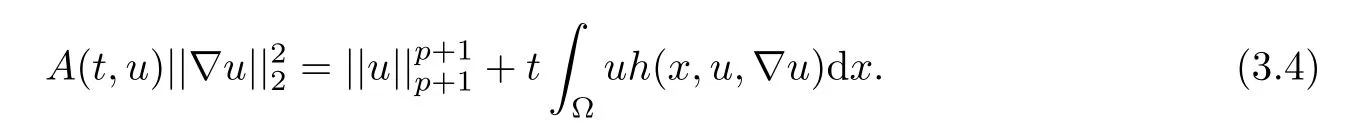
Taking the assumption(H)into account,we can deduce that
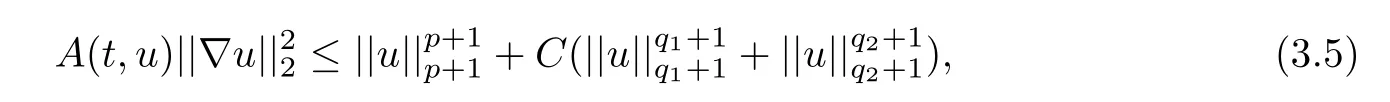
where 0 Since t∈[0,1],α>0,a>0,1 It follows from(3.5)and(3.6)that From the Sobolev embedding theorem and Young’s inequality,we can obtain that where C is a positive constant depending on p,q,qand S. We claim that there exists a universal positive constant R which is independent on t such that||u||≤R,by a standard bootstrap argument.In fact,assume that k∈R.Multiplying(3.1)by|u|u and integrating over ?,we have that By the Sobolev imbedding inequality,we obtain that where Sis the best Sobolev imbedding constant. Combining(3.8),(3.9)and A(t,u)≥1,we deduce that for some universal positive constant C.Thus,by the standard regularity theory of elliptic equations,we know that there exists a positive constant C independent of n such that for some τ∈(0,1),it holds that||v||≤C for any n>n. This contradicts the conclusion of Lemma 3.1. This contradicts the conclusion of Lemma 3.4. Similarly,we can conclude the following result when αq+1 Proof Multiplying the differential equation in problem(3.1)by u and integrating the resulting equation on ?,then considering the assumption(H),we have that Let u(x)=Mv(x),where v(x)is the solution of the following problem: Due to the standard regularity theory of elliptic equations and assumption(H),we can obtain,up to a subsequence,that{v}converges to a positive function v in C(?).Moreover,v satis fies However,due to tβ≤β<λ(?),the problem(3.18)has no positive solution,by the maximum principle.This leads to a contradiction.Thus,there exists a constant r>0 such that for any positive solutions u of problem(3.1),it holds that||u||≥r. Step 2 This contradicts the conclusion of Lemma 3.3. From all of the above,we know that there exists a positive constant R such that,for any solution u of problem(3.1),it holds that||u||≤R. When 1 Theorem 3.7 Moreover,from the Sobolev inequality(3.3)and the Sobolev embedding theorem,we can get that If p+1 Thus,we can obtain that where C depends on t,a,q,α and ?. Thus,from inequality(3.26),it holds that||?u||≤C,where C is a positive constant. Let(??)denote the inverse operator of??.De fine Kby For 0 Therefore,the existence of positive solutions for problem(4.1)is equivalent to finding at least one positive fixed point of K.We set It follows from the maximum principle that Kmaps C into itself.Let Idenote the topological index in C(see[13]).If αq+1 If 0 Hence,for any t∈[0,1],Khas at least one fixed point in D(r,R).Consequently,setting t=1,the problem has at least one solution.Therefore,we obtain the Theorem 1.4. Acknowledgements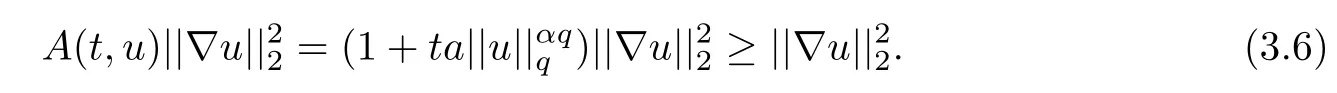
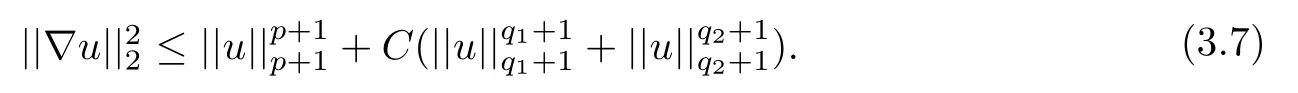
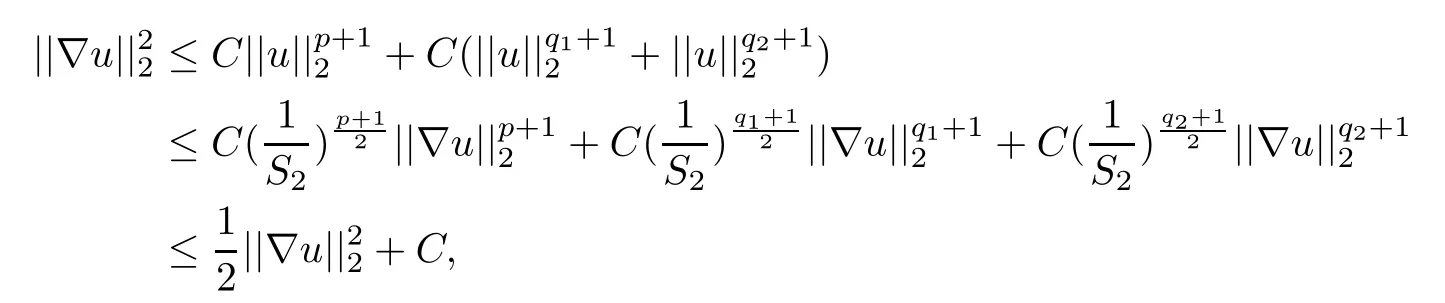
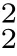
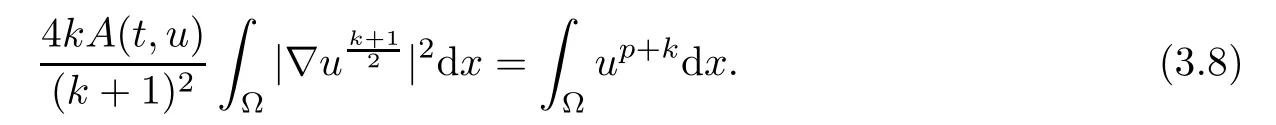


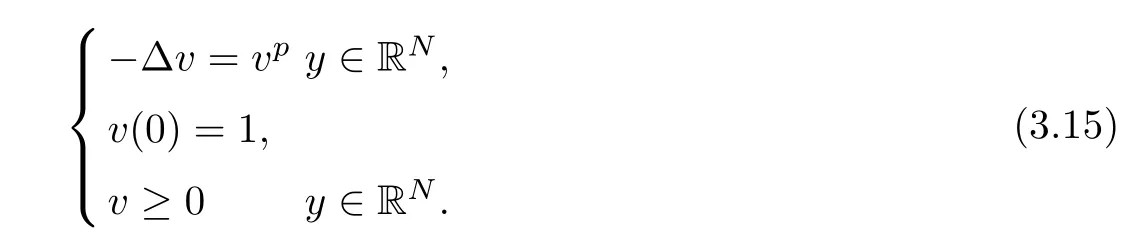
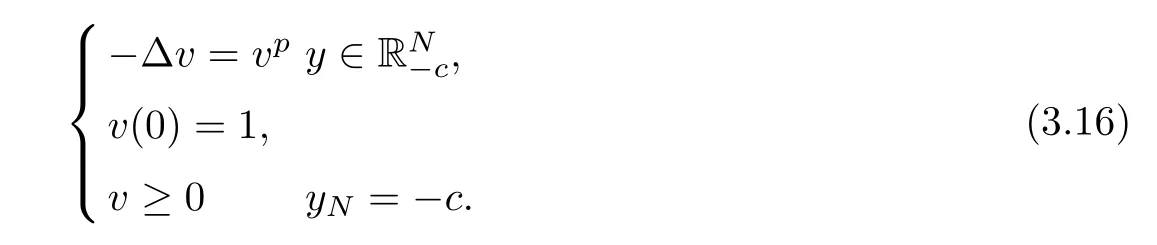
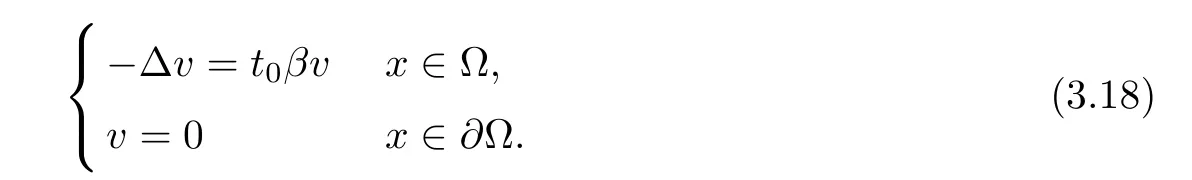
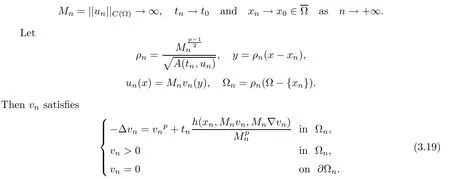

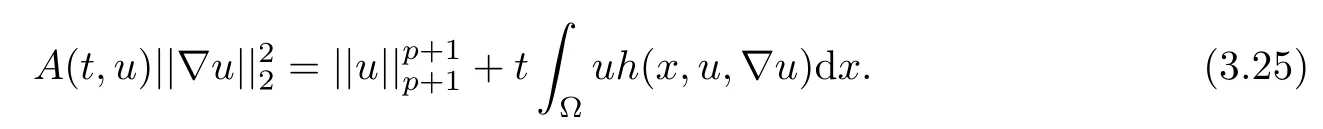
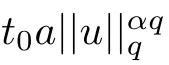
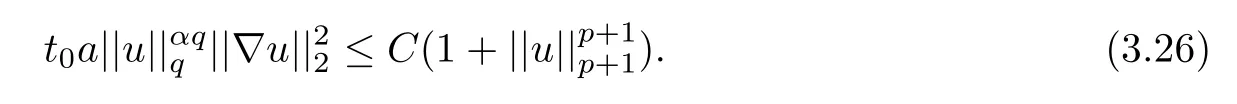
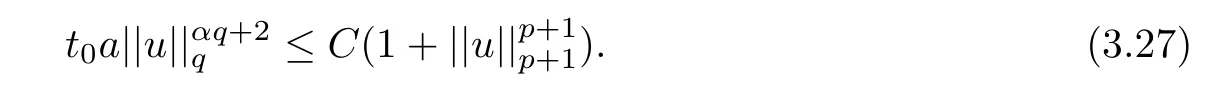
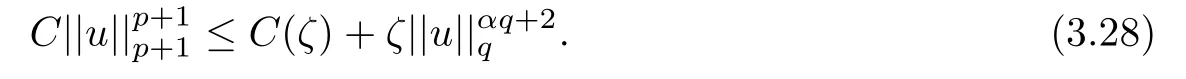

4 Existence Results
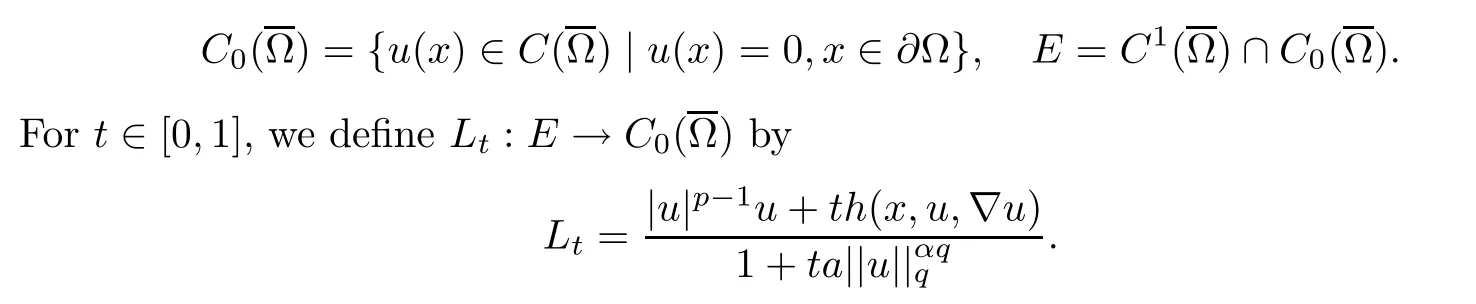
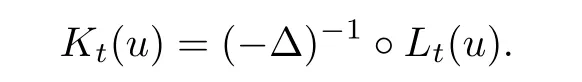
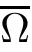
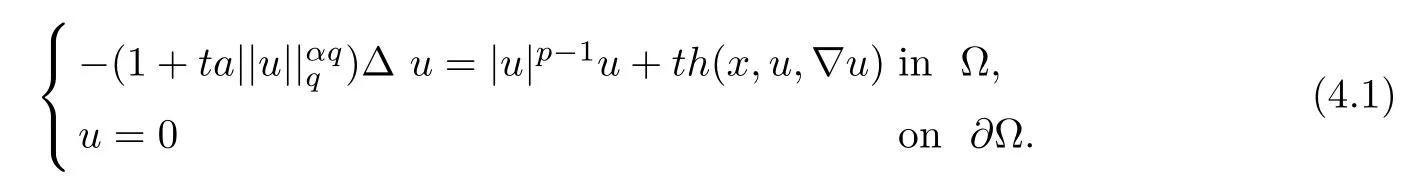
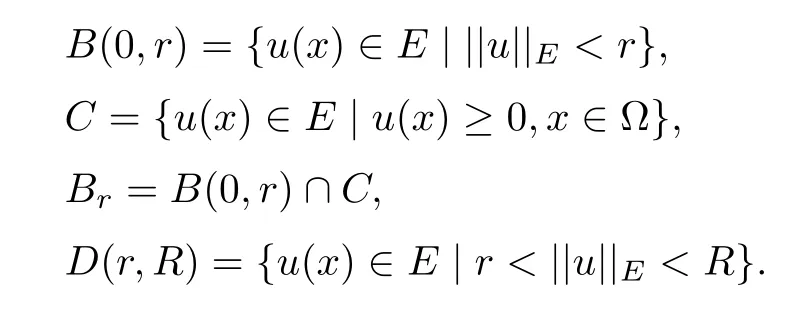


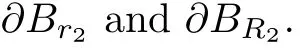
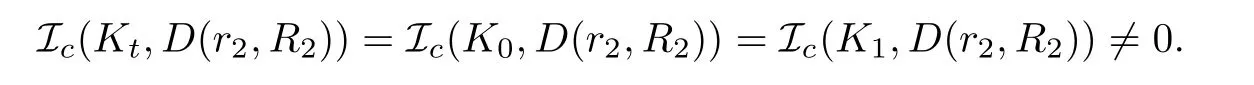
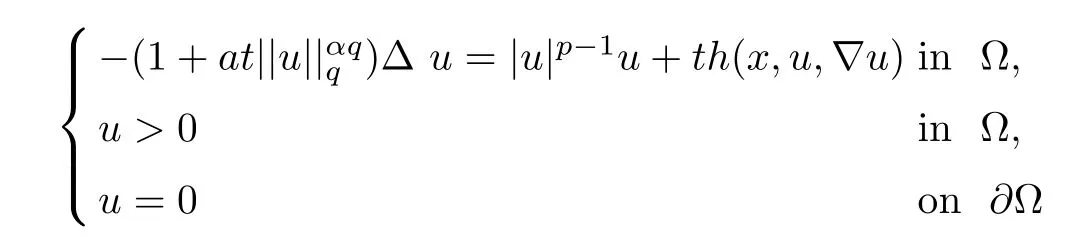
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
