THE CONVERGENCE OF NONHOMOGENEOUS MARKOV CHAINS IN GENERAL STATE SPACES BY THE COUPLING METHOD?
Zhifeng ZHU(朱志鋒)
School of Mathematics and Statistics,Hubei Engineering University,Xiaogan 432000,China Hubei Province Key Laboratory of Systems Science in Metallurgical Process(Wuhan University of Science and Technology),Wuhan 430081,China
E-mail:376574200@qq.com
Shaoyi ZHANG(張紹義)Fanji TIAN(田范基)?
Hubei Key Laboratory of Applied Mathematics,School of Mathematics and Statistics,Hubei University,Wuhan 430062,China
E-mail:zhshaoyi@aliyun.com;tianfj1837@sina.com
Abstract We investigate the convergence of nonhomogeneous Markov chains in general state space by using the f norm and the coupling method,and thus,a sufficient condition for the convergence of nonhomogeneous Markov chains in general state space is obtained.
Key words f norm;coupling;nonhomogeneous Markov chains;convergence
1 Introduction
Because of the requirement of the application of Markov chains in the Monte Carlo method(MCMC),the ergodicity of time-homogeneous Markov chains has attracted considerable interest in the statistical community.The convergence of Markov chains was introduced in Meyn and Tweedie[1],Kartashov[2],Mukhamedov[3],Mukhamedov[4].Currently there already exist mature results on the convergence of the time-homogeneous Markov process in which Probabilistic Distance has been widely employed;see,for example,Theorem 5.22 and Theorem 5.23 of Chen[5].However,the ergodicity of time-homogeneous Markov chains is not enough in the application of MCMC.Therefore,it is necessary to discuss convergence of nonhomogeneous Markov chains.
Since non-homogeneous Markov chains are an extremely difficult aspect in the study of Markov processes,judging the convergence of Markov chains has been the pursuit of many scholars.The Dobrushin-Isaacson-Madsen theorem studies Markov chains in terms of finite state space(Gong and Qian[6]).In this paper,a conclusion about the convergence of nonhomogeneous Markov chains is drawn for general state space.Theorem 1.1(Dobrushin-Isaacson-Madsen theorem)is a special case of Theorem 1.2.The following Dobrushin-Isaacson-Madsen theorem gives a sufficient condition for the convergence of nonhomogeneous Markov chains in finite state space.
De finition
Let v be the signed measure onB
(X),and let g and f be measurable functions onB
(X).De fine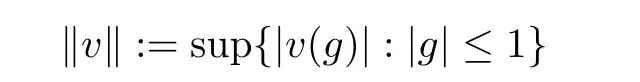
and

De finition
The Markovprocess{Φ,t∈R}is called ergodic if there is a unique invariant measure π that satis fies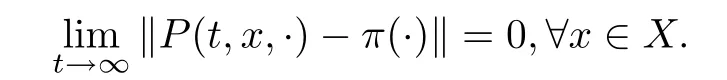
De finition
Let f be measurable function onB
(X).The Markov process{Φ,t∈R}is called f-ergodic if f≥1 satis fies that(i) Φis a positive Harris recurrent and has an invariant measure π;
(ii) π(f)<∞;
(iii)for any initial state of x,
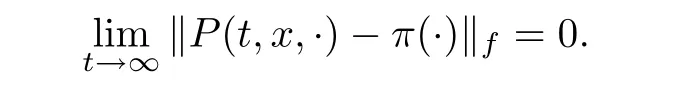
If f≡1,the f norm becomes the total variation norm,and accordingly,the f-ergodic becomes ergodic.
Theorem 1.1
(Dobrushin-Isaacson-Madsen Theorem[6]) Let X={X,X,···,X,···}be a non-homogeneous Markov chain in the finite state space S,and let Pbe the transfer probability matrix of its n-th step.Assume that(A.1)there is a stationary distribution πwhen Pis a homogeneous transfer matrix;
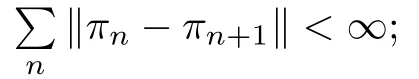
(A.3)these either satisfy the Isaacson-Madsen condition,that for any probability distribution vectorμ,ν on S and with positive integer j,we always get
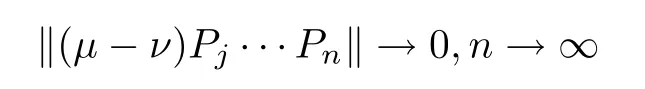
or they satisfy the Dobrushin condition,that for any integer j,if we let P=(P···P)=(P),C(P),i.e.,the contraction coefficient of P,we have
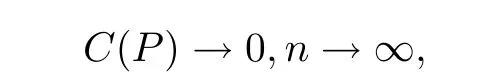
where
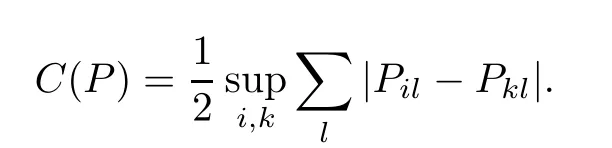
Then,there is a probability measure π on S such that
(1)‖π?π‖→0,n→∞;
(2)for any arbitrary initial distributionμ,the distributionμof the nonhomogeneous Markov chains always has a limit
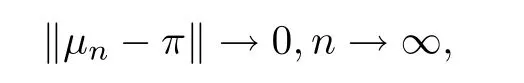
where‖v‖is the total variation norm of the signed measure v on S.
We extend Theorem 1.1 from the finite state space S to the generalPolish space(X,ρ,B
(X)).Let(X,B
(X))be a Polish space,whereB
(X)is an σ algebra generated by a countable subset of X.Throughout the paper,we denote by g a measurable function on X.by v the signed measure onB
(X),and by K a measurable nuclear on(X,B
(X)).We de fine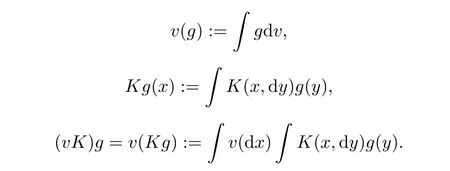
De finition
Let v be the signed measure onB
(X),and let g and f be measurable functions onB
(X).De fine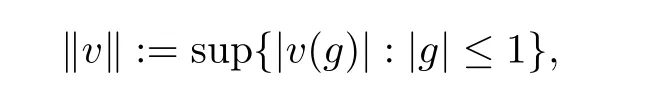
and
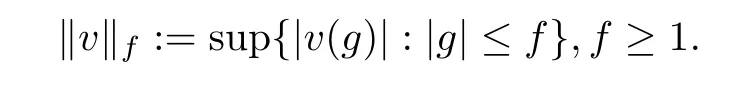
Let ?(x,y):=d(x,y)[f(x)+f(y)],where

B
(X)),where the transfer probability of its n-th step can be written as P(Φ∈A|Φ=x}:=P(x,A).Furthermore,if P=P=···=P,then we call Φ a time-homogeneous Markov chain.Moreover,let us de fineP
(X)as the all probability measures on X,and xas any given point on X,and also setM
={μ∈P
(X):R?(x,x)μ(dx)<∞}.Theorem 1.1 introduces the convergence of nonhomogeneous Markov chains in the finite state space.In practice,however,this is not enough.Zhang[7]introduced the existence of Markov chains coupling.Zhu and Zhang[8]studied the convergenceof nonhomogeneous Markov chains in general state space using Probabilistic Distance and the coupling method.Now,we will study the convergence of nonhomogeneous Markov chains in general state space using the f norm and the coupling method.
Theorem 1.2
Let(X,B
(X))be a Polish space,and let Φ={Φ,Φ,···,Φ,···}be a nonhomogeneous Markov chain on X.Furthermore,let{P;n=1,2,···}be the corresponding sequence of probability kernel of Φ.Assume that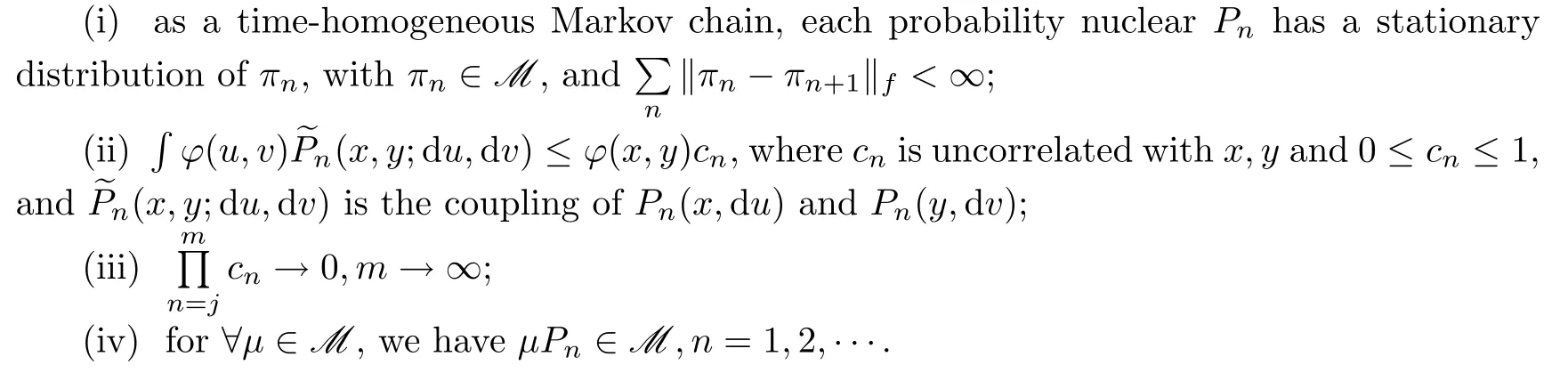
M
such that,for a probability measureμinM
,we have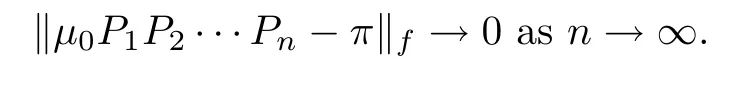
Remark 1
In general,the condition in the theorem(iv)is easily veri fiable.In particular,this condition is automatically satis fied when ? is a bounded distance.Remark 2
When f≡1,the f norm becomes the total variation norm,in which case Theorem 1.2 is considered,like Theorem 1.1,a general state.2 Preliminaries
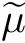
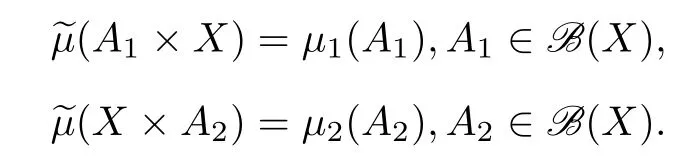
We denote by K(μ,μ)all coupling ofμandμ.
De finition
Lettingμandμbe probability measures in the Polish space(X,ρ,B
(X)),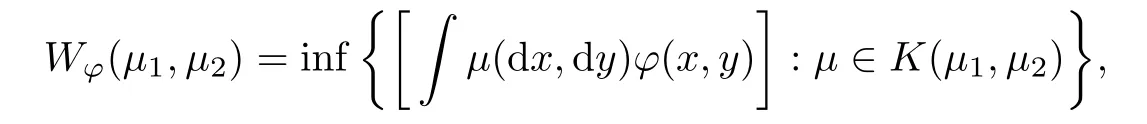
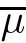
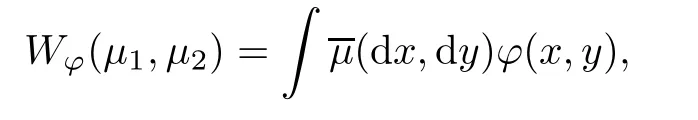
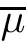
Lemma 2.1
(Lindvall[9]) Letμandμbe probability measures onB
(X),and let
Then,we have the following:
1.0 ≤γ≤1;
2.vand vare two probability measures onB
(X);3.Q is a probability measure onB
(X)×B
(X).Furthermore,let
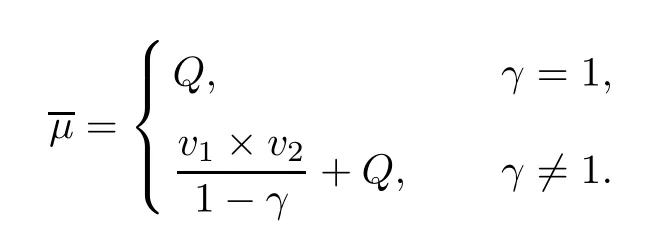
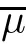
Lemma 2.2
Letμ,μbe probability measures.Hence,we obtain
M
.Lemma 2.4
Letμ,μbe probability measures,and let Pbe a probability kernel on Polish space(X,ρ,B
(X)).Assume that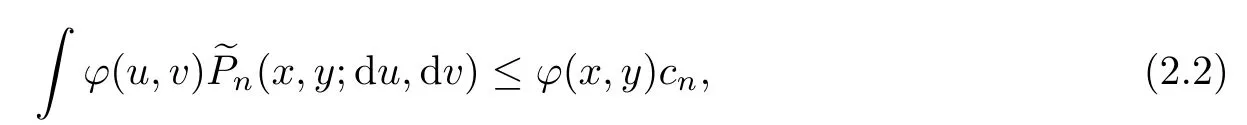
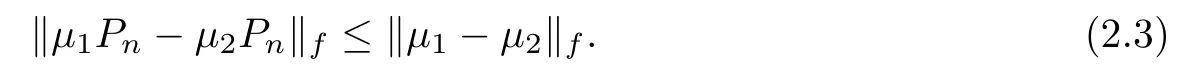
Proof
From(2.2),we obtain thatAs the years passed, other occasions--birthdays, recitals13, awards, graduations--were marked with Dad s flowers. My emotions continued to seesaw14 between pleasure and embarrassment.
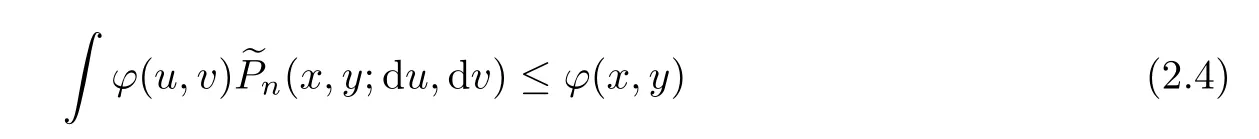
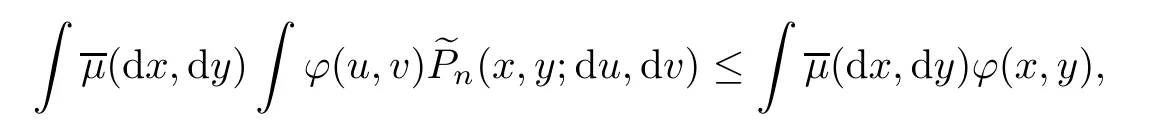
which means that
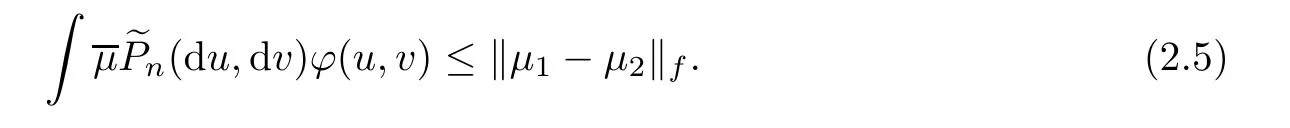
Now we only need to prove that
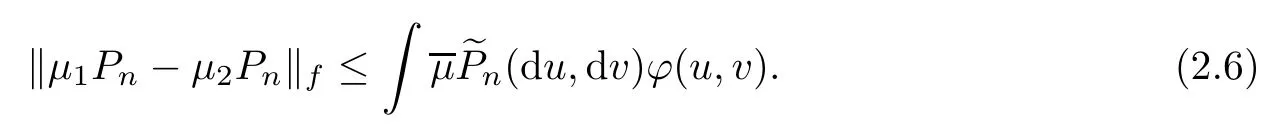

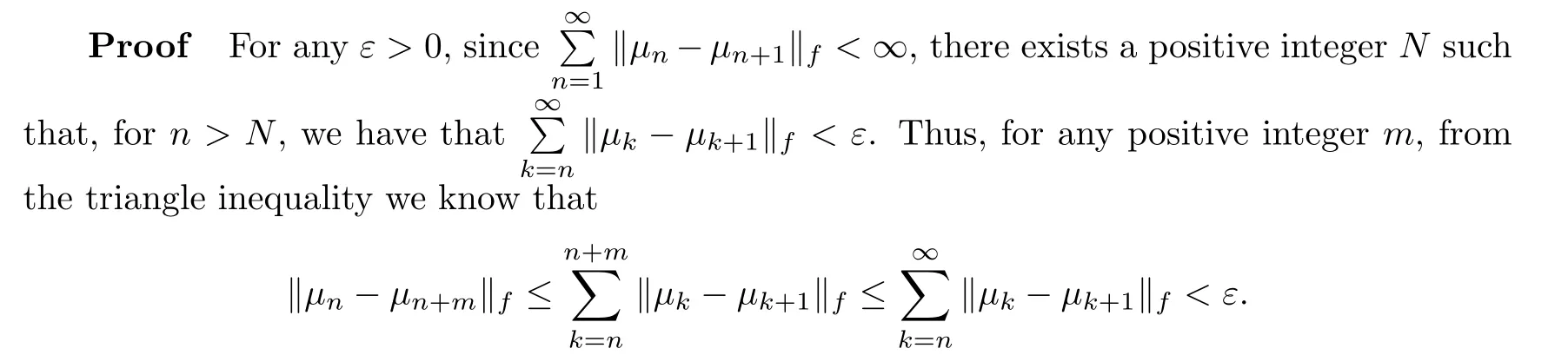
Therefore{μ:n≥1}is a Cauchy sequence.
3 Proof of the Main Result
Next,we use three steps to prove The theorem 1.2:
(a)For?μ,μ∈M
and any positive integer j,we have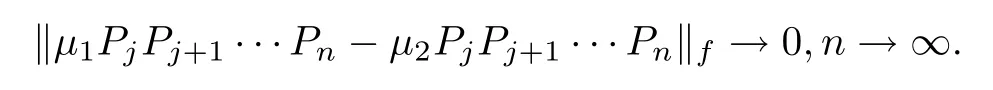
M
such that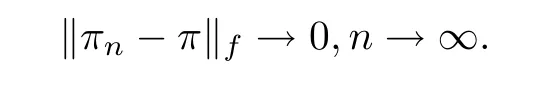
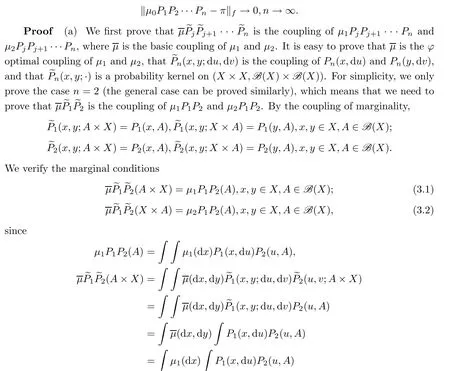

M
,W}is a complete metric space.Lemma 2.8 implies that{π:n≥1}is a Cauchy sequence on{M
,W}.Then there exists π∈M
such that‖π?π‖→0,n→∞.Thus(b)holds.(c)We will prove that for?ε>0,?N∈zsuch that for n>N we have that

For any positive integer j≤n,by triangle inequality we have
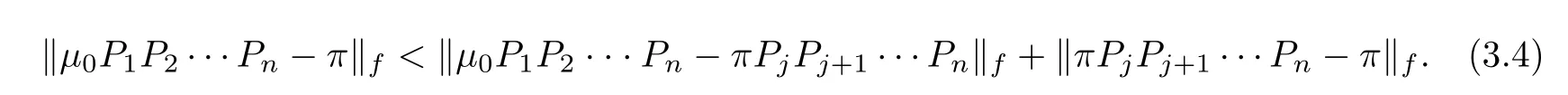
Applying the condition πP=πrepeatedly to the second item above,we can deduce that

We again apply(3.9)and(3.10)to(3.4),and thus(3.3)holds.The proof of Theorem 1.2 is completed.
4 Remark on Theorem 1.2
Remark 1
The condition(ii)can be replaced by the following:there is cuncorrelated with x,y that satis fies 0≤c≤1 such tha,t for?μ,μ∈M
,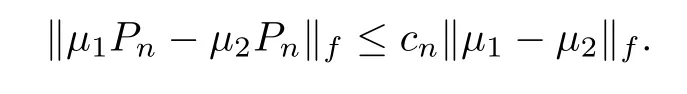
Remark 2
The condition(ii)can be replaced by the following:there is cuncorrelated with x,y that satis fies 0≤c≤1 such that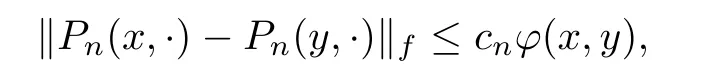
where ?(x,y):=d(x,y)[f(x)+f(y)],and f≥1 is a measurable function.
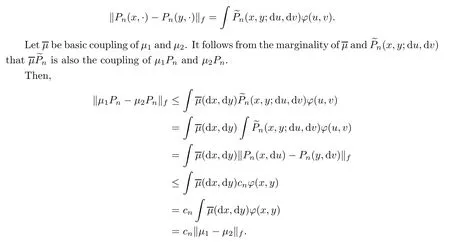
Remark 3
The condition(iv)can be replaced by P∈M
.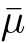
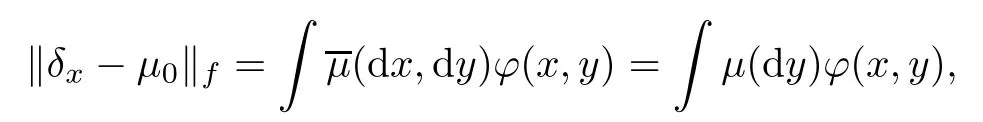
M
,μ∈M
,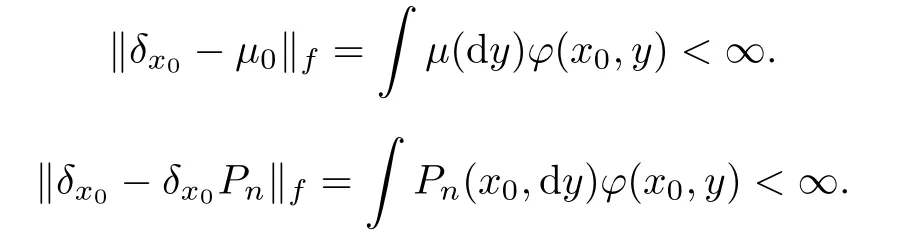
Thus,
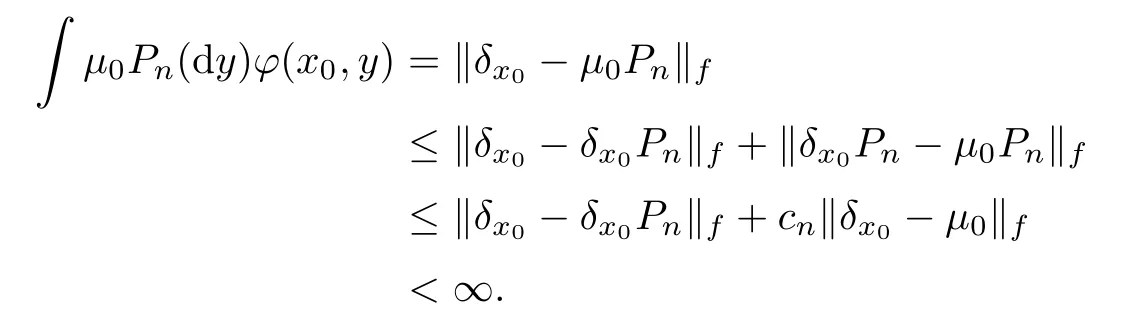
M
. Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- THE UNIQUENESS OF THE LpMINKOWSKI PROBLEM FOR q-TORSIONAL RIGIDITY?
- HYERS–ULAM STABILITY OF SECOND-ORDER LINEAR DYNAMIC EQUATIONS ON TIME SCALES?
- ON NONCOERCIVE(p,q)-EQUATIONS?
- POSITIVE SOLUTIONS OF A NONLOCAL AND NONVARIATIONAL ELLIPTIC PROBLEM?
- A PENALTY FUNCTION METHOD FOR THE PRINCIPAL-AGENT PROBLEM WITH AN INFINITE NUMBER OF INCENTIVE-COMPATIBILITY CONSTRAINTS UNDER MORAL HAZARD?
- THE INITIAL BOUNDARY VALUE PROBLEMS FOR A NONLINEAR INTEGRABLE EQUATION WITH 3×3 LAX PAIR ON THE FINITE INTERVAL?
