一類平坦半環(huán)生成的簇

高子?xùn)|,任苗苗

(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)

1 引言和預(yù)備知識(shí)

設(shè) V是同型代數(shù)作成的類.若 V對(duì)子代數(shù),直積和同態(tài)像封閉,則稱其為簇.由Birkhoff定理可知,一個(gè)同型代數(shù)類是簇當(dāng)且僅當(dāng)它是等式類,即滿足某個(gè)恒等式集合的代數(shù)的全體.若簇V可由有限個(gè)恒等式確定,則稱V是有限基底的,否則稱V為非有限基底的.簇的有限基底問(wèn)題是問(wèn)它是否為有限基底的,該問(wèn)題是簇的核心問(wèn)題之一.設(shè)K是一些同型代數(shù)作成的類,用V(K)表示由K生成的簇,即包含K的最小的簇.若K中只有一個(gè)成員A,則簡(jiǎn)記為V(A).由Tarski定理可知,V(K)=HSP(K),其中H,S,P分別是同態(tài)像,子代數(shù)和直積類算子.

設(shè)(Ai)i∈I是一族同型代數(shù),A是的子代數(shù).若對(duì)于任意j∈I,用

表示自然投射,均有πj(A)=Aj,則稱A是 (Ai)i∈I的次直積.如果代數(shù)A只有平凡的次直積分解,即對(duì)于任意一族同型代數(shù) (Ai)i∈I,A是 (Ai)i∈I的次直積蘊(yùn)含著存在i∈I,使得AAi,則A被稱為次直不可約的.若A是非平凡的代數(shù),則A是次直不可約的當(dāng)且僅當(dāng)它有最小的非平凡同余.由文獻(xiàn)[1]知,簇V的每個(gè)成員都可表示為它的一些次直不可約成員的次直積.這表明簇V完全被它的次直不可約成員所確定.因此,研究簇的次直不可約成員是簇的又一核心問(wèn)題之一.

定義 1.1[2]設(shè)S是半群,A是S的任一非空子集.若AA?A,則稱A為S的子半群,記作A≤S.若AS,SA?A,則稱A為S的理想,記作AS.

設(shè)I是半群S的理想.則ρI(I×I)∪1S稱為S上(由I確定)的Ress同余[3].其對(duì)應(yīng)的商半群為

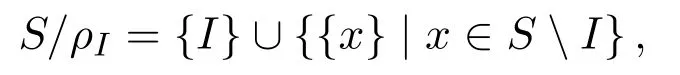
簡(jiǎn)記為S/I.容易驗(yàn)證,I是商半群S/I的零元,因此也可將S/I視為(SI)∪{0}.反之,則有如下命題:

命題1.1設(shè)S是含0的半群.若S上有同余ρ=(0/ρ×0/ρ)∪1S,則I0/ρS,進(jìn)而ρ=ρI是半群S上的Ress同余.

證明設(shè)a∈0/ρ,s∈S.由aρ0,sρs,且ρ是S上的同余,可得

asρ0s=0,saρs0=0.

也即as,sa∈0/ρ.這表明I0/ρS,進(jìn)而ρ=ρI是半群S上的Ress同余.

定義 1.2[2]設(shè)S是含0的半群.若對(duì)于任意a∈S,存在n∈N,使得an=0,則稱S為nil-半群.

下面將給出nil-半群的0-極小理想[2]的刻畫:

命題 1.2設(shè)S是nil-半群.若I是S的0-極小理想,則|I|=2.

證明任取a,b∈I{0}.由I的 0-極小性可知,S1aS1=S1bS1.故存在x,y,u,v∈S1,使得b=xay,a=ubv.因此

a=(ux)a(yb)= ···(ux)na(yb)n= ···.

結(jié)合S是nil-半群以及a0可知,x=y=u=v=1.這表明a=b.故|I|=2.

定義 1.3[2]設(shè)S是含0的半群.若滿足:

則稱S為0-可消半群.

在下一節(jié)中,將討論0-可消半群與平坦半環(huán)的關(guān)系.下面介紹半環(huán)的一些基本概念:

定義 1.4[2]設(shè) (S,+,·)是(2,2)型代數(shù).若滿足:

(1)(S,+),(S,·) 是半群;

(2)(a+b)c=ac+bc,c(a+b)=ca+cb,?a,b,c∈S,則稱 (S,+,·)為半環(huán),簡(jiǎn)記為S.

若半環(huán)S滿足

a+b=b+a,a+a=a,?a,b∈S,

則稱S為加法冪等元半環(huán),簡(jiǎn)記為ai-半環(huán).

對(duì)于ai-半環(huán)S,定義偏序關(guān)系如下:

(?a,b∈S)a≤b?a+b=b.

容易驗(yàn)證,(S,≤)是(上)半格,因此ai-半環(huán)也被稱作半格序半群.

定義 1.5[3]設(shè)S是半環(huán),A是S的任一非空子集.若A≤(S,+)且A≤(S,·),則稱A是S的子半環(huán),記作A≤S.若A(S,+)且A(S,·),則稱A是S的理想,記作AS.

近二十年來(lái),ai-半環(huán)簇的研究是非?；钴S的[3-15].文獻(xiàn)[11-12]研究了x2≈x確定的ai-半環(huán)簇.文獻(xiàn)[3]給出了第一個(gè)非有限基底的有限ai-半環(huán)的例子.文獻(xiàn)[5]給出了恒等式xn≈xm確定的ai-半環(huán)簇的自由對(duì)象的模型.文獻(xiàn)[6]證明了若ai-半環(huán)滿足恒等式xn≈x,則它的乘法導(dǎo)出是正則純正密碼群.文獻(xiàn)[7-8]證明了滿足恒等式x3≈x的ai-半環(huán)簇共有179個(gè),且這些簇都是有限基底的.文獻(xiàn)[10]研究了所有二階ai-半環(huán)生成的簇,證明了它的子簇格是64階的布爾代數(shù).文獻(xiàn)[13]研究了三階ai-半環(huán)的有限基底問(wèn)題.在上述文獻(xiàn)的基礎(chǔ)上,本文將主要研究次直不可約的平坦半環(huán),以及一類平坦半環(huán)生成的簇.給出次直不可約的nil-平坦半環(huán)的一些等價(jià)刻畫,證明當(dāng)n≤3時(shí),平坦半環(huán)S(x1x2···xn)均是有限基底的.

2 次直不可約的 nil-平坦半環(huán)

定義 2.1[1]設(shè)S是含乘法零元的半環(huán).若其加法導(dǎo)出(S,+)滿足:

則稱S是平坦半環(huán).

為了方便起見,將上述的“加法”稱為 flat加法.容易驗(yàn)證,平坦半環(huán)S是一類特殊的ai-半環(huán),其乘法零元亦是加法零元,且當(dāng)|S|≥2時(shí),(S,≤)是高度為1的半格.下面的引理將說(shuō)明平坦半環(huán)與0-可消半群之間的關(guān)系:

引理 2.1設(shè)S是平坦半環(huán),則其乘法導(dǎo)出 (S,·)是 0-可消半群.反之,對(duì)于任一0-可消半群(S,·),都可以定義 flat加法,使得(S,+,·)成為平坦半環(huán).

證明設(shè)S是平坦半環(huán).任取a,b,c∈S,若ab=ac0,則ab+ac=a(b+c)0,因此b+c0,故b=c.同理可知,由ba=ca0亦可推出b=c.因而,(S,·)是 0-可消半群.

反之,設(shè) (S,·)是 0-可消半群,定義上述 flat加法.下面只需驗(yàn)證乘法 “·”對(duì)加法“+”具有左右分配律即可.任取a,b,c∈S:

(i)若b=c,則a(b+c)=ab=ab+ac.

(ii)若bc,則a(b+c)=a0=0.斷言ab+ab=0,否則ab+ac0,進(jìn)而ab=ac0,再由S的0-可消性可知,b=c,矛盾.因此,a(b+c)=0=ab+ac.

綜上所述,a(b+c)=ab+ac.同理可知,(b+c)a=0=ba+ca.因此,(S,+,·)是平坦半環(huán).

上述引理說(shuō)明,平坦半環(huán)與0-可消半群具有一一對(duì)應(yīng)的關(guān)系.因此構(gòu)造具體的平坦半環(huán)時(shí),只需構(gòu)造出0-可消半群,然后在此基礎(chǔ)上賦予 flat加法即可.容易驗(yàn)證,對(duì)于任意可消半群S(或更為特殊的自由半群,群等),直接添加零元,即可得到0-可消半群S0.但這并不意味著0-可消半群都是通過(guò)這種方式得到的,例如null-半群S(也即滿足S2={0}的半群).下面將介紹一類重要的0-可消半群:

命題 2.1設(shè)W是自由半群X+的任一非空子集.令

則 (S(W),·)是 0-可消半群.

證明直接驗(yàn)證可知,(S(W),·)滿足結(jié)合律以及 0-可消性.為了揭示 (S(W)與X+0的關(guān)系,取I=X+S(W),則有IX+0且X+0/I～=S(W).而X+0是 0-可消的,進(jìn)而容易驗(yàn)證X+0/I亦為0-可消半群,因此S(W)也是0-可消半群.

賦予 flat加法可知,(S(W),+,·)是平坦半環(huán),簡(jiǎn)記為S(W).當(dāng)W={w}為單點(diǎn)集時(shí),也可將S({w})簡(jiǎn)記為S(w).下一節(jié)將重點(diǎn)討論S(w)的相關(guān)問(wèn)題.在此之前,首先說(shuō)明平坦半環(huán)的子半環(huán)與商半環(huán)的特點(diǎn)以及證明平坦半環(huán)上的同余恰為Ress同余.

命題 2.2設(shè)S為平坦半環(huán),則有如下結(jié)論成立:

(1)S的任一子半環(huán)T均為平坦半環(huán),其中子半環(huán)T按(2,2,0)型代數(shù)考慮,也即T需含有S中的零元;

(2)S的任一商半環(huán)S/ρ均為平坦半環(huán);

(3)設(shè)A是S的任一非空子集,則

〈A〉={a1a2···an|ai∈S,i=1,···,n,n∈N}∪{0}.

其中〈A〉表示S中由子集A生成的子半環(huán),也即S中包含A的最小子半環(huán);

(4)設(shè)A是S的任一非空子集,則S1AS1是S中包含子集A的最小理想.

證明(1)設(shè)T為S的任一子半環(huán).由引理2.1可知,只需驗(yàn)證(T,·)為0-可消半群即可.由于S中的零元在T中,從而亦是T的零元,因此結(jié)論顯然成立.

(2)由引理2.1可知,只需驗(yàn)證(S/ρ,·)為0-可消半群即可.任取若,則有.由引理2.2可知,因此,ab=ac0.結(jié)合S的0-可消性可知,b=c,也即=.同理可知,由亦可推出=.故(S/ρ,·)為0-可消半群,結(jié)論得證.

(3)記等式右邊的集合為B.若T是包含A的任一子半環(huán),則有B?T.因此只需證明B是子半環(huán)即可.易知B≤(S,·).由0∈S結(jié)合 flat加法的性質(zhì)可得,B≤(S,+).因此B是S的子半環(huán),結(jié)論得證.

(4)類比(3)證明可知,結(jié)論顯然成立.

引理 2.2設(shè)S為平坦半環(huán).若ρ為(S,+)上的同余,則有

ρ=(0/ρ×0/ρ)∪1S=ρI,

其中I=0/ρ是 (S,+)上的理想.反之,若I是S是任一含 0的非空子集,則有I(S,+).

證明令ρ為(S,+)上的同余.任取a,b∈S且ab.若aρb,則有

a=a+aρa(bǔ)+b=0,b=b+bρa(bǔ)+b=0.

因此a,b∈0/ρ,即有ρ=(0/ρ×0/ρ)∪1S.再由命題 1.1可知,I=0/ρ是 (S,+)上的理想,進(jìn)而ρ=ρI.

反之,若I是S是任一含0的非空子集,則有I+S=S+I=I.由定義可知,I(S,+).

上述引理表明(S,+)上的同余恰為Ress同余,而(S,+)上的理想也恰為S的某一含0的非空子集,且二者具有一一對(duì)應(yīng)的關(guān)系.進(jìn)而有如下命題:

命題 2.3設(shè)S為平坦半環(huán),ρ?S×S.則ρ是S上的同余,當(dāng)且僅當(dāng)存在I(S,·),使得ρ=ρI.

證明充分性.若存在I(S,·),使得ρ=ρI,則ρI是 (S,·)上的同余.而I是含 0的非空子集,由引理 2.2可知,I(S,+).因此,ρI也是 (S,+)上的同余,進(jìn)而ρ=ρI是S上的同余.

必要性.若ρ是S上的同余,則ρ是其加法導(dǎo)出(S,+)上的同余.故由引理2.2可知,ρ=(0/ρ×0/ρ)∪1S=ρ0/ρ.結(jié)合ρ亦是其乘法導(dǎo)出 (S,·)上的同余,由命題 1.1可知,0/ρ(S,·).這表明ρ=ρI,其中I0/ρ(S,·).

由上述命題可知,平坦半環(huán)上的同余均為Ress同余,且與乘法導(dǎo)出的理想具有一一對(duì)應(yīng)的保序關(guān)系.進(jìn)而有如下推論:

推論 2.1設(shè)S是非平凡的平坦半環(huán).則S是次直不可約的,當(dāng)且僅當(dāng)(S,·)有唯一的0-極小理想.

定義 2.2設(shè)S是半環(huán).若 (S,·)是 nil-半群,則稱S為nil-半環(huán).

定義 2.3[2]設(shè)S是平坦半環(huán).若存在ω∈S{0},使得Sω=ωS={0},則稱ω是S的零化子.

命題 2.4設(shè)S是非平凡的nil-平坦半環(huán).則S是次直不可約的,當(dāng)且僅當(dāng)S有唯一的零化子ω.

證明必要性.由于S是次直不可約的,由推論2.1可知,(S,·)有唯一的0-極小理想I.而 (S,·)是 nil-半群,結(jié)合命題 1.2可知 |I|=2,不妨記為I={0,ω}.由理想的定義可知,任取s∈S,sω∈I.若sω=ω,則

ω=sω=s2ω=s3ω= ···,

而 (S,·)是 nil-半群,故ω=0,矛盾.因此,sω=0.同理可知ωs=0,從而ω是S的零化子.下證唯一性,設(shè)ω′是S的任一零化子.則{0,ω′}是 (S,·)的 0-極小理想.由 0-極小理想的唯一性可知,{0,ω′}={0,ω}.因此,ω′=ω.

充分性.若S有唯一的零化子ω,則I?{0,ω}是 (S,·)的 0-極小理想.欲證S是次直不可約的,由推論 2.1可知,只需說(shuō)明 (S,·)有唯一的 0-極小理想即可.設(shè)J為(S,·)的一個(gè)0-極小理想.由命題1.2可知,|J|=2.不妨設(shè)J={0,a}.由必要性證明可知,a是S的一個(gè)零化子.結(jié)合S有唯一的零化子可知,a=ω.因此,I=J.

若取W為自由半群X+的有限非空子集,則有S(W)是一個(gè)有限的nil-平坦半環(huán),且W中的極大字恰為S(W)的零化子.因此,有如下推論:

推論 2.2設(shè)W為自由半群X+的有限非空子集.則下列命題等價(jià):

(1)S(W)是次直不可約的;

(2)W中有唯一的極大字;

(3)存在w∈W,使得S(W)=S(w).

3 一類平坦半環(huán)生成的簇

從上一節(jié)可知,平坦半環(huán)是特殊的ai-半環(huán),且關(guān)于子代數(shù)和商代數(shù)封閉.但平坦半環(huán)的直積未必是平坦半環(huán),因此所有的平坦半環(huán)作成的類并不是一個(gè)簇,進(jìn)而考慮由所有的平坦半環(huán)生成的簇,記作F.顯然F是ai-半環(huán)簇AI的子簇.結(jié)合文獻(xiàn)[4]可得下列兩個(gè)引理:

引理 3.1F是由ai-半環(huán)簇AI填加下列恒等式所確定的簇:

a(x+y)b+c(x+y)d≈a(x+y)b+cxd.

其中,a,b,c,d中的任意一個(gè)均可為空.

引理3.2F中的次直不可約成員必為平坦半環(huán).

接下來(lái)將主要討論V(S(x1x2···xn))的有限基問(wèn)題.首先,記Vn(n∈N)為F添加如下恒等式確定的簇:

其中,v∈{x1,x2,···,xk}+且vx1x2···xk;在 (5)式中,a,b中至少有一個(gè)為空;在(6)-(8)式中,a,b中任意一個(gè)均可為空.

顯然S(x1x2···xn)滿足上述恒等式,因此 V(S(x1x2···xn))?Vn,n∈N.下面將證明n=1,2,3時(shí),V(S(x1x2···xn))=Vn.在此之前,先說(shuō)明 Vn中次直不可約成員的一些基本性質(zhì):

引理 3.3設(shè)S是Vn中任一非平凡次直不可約成員.則有如下結(jié)論成立:

(1)S是平坦半環(huán),它有唯一的零化子ω,進(jìn)而{0,ω}是S的唯一0-極小理想;

(2)若存在k∈N,使得Sk={0}且Sk+1{0},則Sk={0,ω};

(3) 若存在b1,b2,···,bn,c1,c2,···,cn∈S, 使得b1b2···bn=c1c2···cn=ω,則有bi=ci,1≤i≤n;

(4) 若存在a1,a2,···,am∈S使得a1a2···am0,則

〈a1,a2,···,am〉=S(x1x2···xm),

其中〈a1,a2,···,am〉表示由{a1,a2,···,am}生成的子半環(huán).

證明(1)由于S是Vn中的次直不可約成員,進(jìn)而亦是F中的次直不可約成員.故由引理3.2可知,S是平坦半環(huán).根據(jù)恒等式(2)可知,(S,·)是nil-半群,于是S是次直不可約nil-平坦半環(huán).結(jié)合命題2.4可知,S有唯一的零化子ω.進(jìn)而,{0,ω}是S的唯一0-極小理想.

(2)若存在k∈N,使得Sk{0}且Sk+1={0}.任取s=s1s2···sk∈Sk且s0.由于I是S的 0-極小理想,因而I?S1sS1.故存在u,v∈S1,使得ω=usv=us1s2···skv.結(jié)合Sk+1={0}可知,u=v=1,也即s=ω.這表明Sk={0,ω}.

(3)由恒等式(3)可知,結(jié)論顯然成立.

(4)根據(jù)命題2.2(3)可知,只需證明:

〈a1,a2,···,am〉={aiai+1···aj|1≤i≤j≤m}∪{0}.

記等式右邊的集合為A.顯然A?〈a1,a2,···,am〉,所以只需說(shuō)明〈a1,a2,···,am〉?A,且A中元素互不相同即可.任取v∈{a1,a2,···,am}+且va1a2···am.斷言v=0,否則根據(jù)ω∈S1vS1可知,存在a,b∈S1使得ω=avb.進(jìn)而a1a2···am+avb=0,這與恒等式 (6)矛盾,于是〈a1,a2,···,am〉=A.若A中有兩個(gè)元素相同,不妨設(shè)aiai+1···aj=akak+1···a?,其中 1≤i≤j,k≤?.下面分兩種情形討論:

(i)若j≤k,則利用恒等式(1)和恒等式(4)可知,任取a,b∈S,總有a2=aba=0.因此得到a1a2···am=0,矛盾.

(ii) 若j>k,記ai···ak=x,ak+1···aj=y,aj+1···a?=z,則有xy=yz0,于是xy+yz0,這與恒等式(2)矛盾.

綜上所述,〈a1,a2,···,am〉=S(x1x2···xm).

由恒等式(1)得,Vn,V(S(x1x2···xn))均為局部有限簇.再結(jié)合

V(S(x1x2···xn))?Vn

可知,只需證 Vn中任一 (有限)非平凡次直不可約成員,均落在 V(S(x1x2···xn))即可.

定理3.1V(S(x1))=V1.

證明任取V1中的非平凡次直不可約成員S.由引理3.3(1)可知,S是次直不可約的平坦半環(huán),且有唯一的0-極小理想{0,ω}.結(jié)合恒等式(1)可知,S2={0},從而(S,·)為 null-半群.因此S的任一含0非空子集均為S的理想.結(jié)合0-極小理想的唯一性可知,S={0,ω}S(x1)∈V(S(x1)).

定理3.2V(S(x1x2))=V2.

證明任取V2中的非平凡次直不可約成員S.由引理3.3(1)可知,S是次直不可約的平坦半環(huán),且有唯一的0-極小理想{0,ω}.結(jié)合恒等式(1)可知,S3={0}.因此,分下列兩種情形討論:

(i)S2={0}.由定理 3.1可知,SS(x1)∈V(S(x1x2)).

(ii)S2{0}.由引理 3.3(2)可知,S2={0,ω}.于是存在x1,x2∈S,使得x1x2=ω0.由引理 3.3(4)可知,〈x1,x2〉=S(x1x2).斷言S=S(x1x2),否則存在e∈SS(x1x2).結(jié)合ω∈S1eS1可知,存在a,b∈S1,使得ω=aeb.結(jié)合S3={0}且eω可知,a=1,b∈S或b=1,a∈S.再由引理3.3(3)可知,e=x1,b=x2或a=x1,e=x2,這與e∈SS(x1x2)矛盾.因此S=S(x1x2)∈V(S(x1x2)).

為了更好的刻畫Vn,接下來(lái)引入“0-ω直并”的概念.進(jìn)而說(shuō)明V(S(x1x2···xn))中具有一類非?！暗湫汀钡拇沃辈豢杉s成員.

設(shè) (Si)i∈I是一族次直不可約的 nil-平坦半環(huán),且滿足Si∩Sj={0,ω},i,j∈I且ij,其中,ω是Si(i∈I)的唯一零化子.令.任取a,b∈S,定義