EXISTENCE AND UNIQUENESS OF THE GLOBAL L1 SOLUTION OF THE EULER EQUATIONS FOR CHAPLYGIN GAS?
(陳停停)
School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China
E-mail:chenting0617@163.com;chentt@cug.edu.cn
Aifang QU(屈愛芳)?
Department of Mathematics,Shanghai Normal University,Shanghai 200234,China
E-mail:afqu@shnu.edu.cn
Zhen WANG(王振)
School of Science,Wuhan University of Technology,Wuhan 430070,China
E-mail:zwang@whut.edu.cn;zhenwang@wipm.ac.cn
Abstract In this paper,we establish the global existence and uniqueness of the solution of the Cauchy problem of a one-dimensional compressible isentropic Euler system for a Chaplygin gas with large initial data in the space The hypotheses on the initial data may be the least requirement to ensure the existence of a weak solution in the Lebesgue measurable sense.The novelty and also the essence of the difficulty of the problem lie in the fact that we have neither the requirement on the local boundedness of the density nor that which is bounded away from vacuum.We develop the previous results on this degenerate system.The method used is Lagrangian representation,the essence of which is characteristic analysis.The key point is to prove the existence of the Lagrangian representation and the absolute continuity of the potentials constructed with respect to the space and the time variables.We achieve this by finding a property of the fundamental theorem of calculus for Lebesgue integration,which is a sufficient and necessary condition for judging whether a monotone continuous function is absolutely continuous.The assumptions on the initial data in this paper are believed to also be necessary for ruling out the formation of Dirac singularity of density.The ideas and techniques developed here may be useful for other nonlinear problems involving similar difficulties.
Key words Compressible Euler equations;linearly degenerate fields;initial data in space without uniform bounds;global well-posedness;regularity
1 Introduction
We are concerned with the Cauchy problem of isentropic gas dynamics for large initial data in thespace.One-dimensional isentropic gas dynamics are governed by the compressible Euler equations
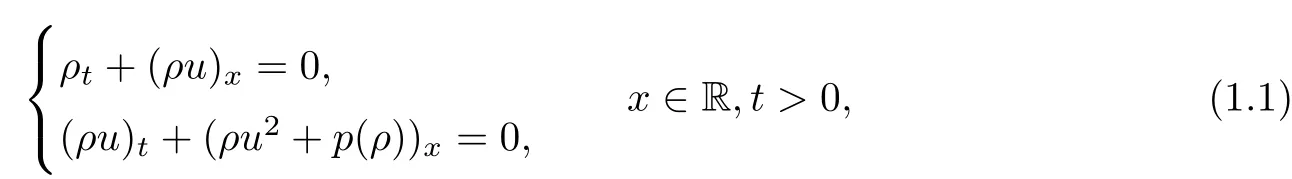
where ρ,u and p represent the mass density,the velocity and the pressure of the flow.The sound speed c≥0 is given by c2=?p/?ρ.

Chaplygin gas is not only a suitable mathematical approximation for calculating the lifting force on the wing of an airplane in aerodynamics,but is also being proposed as a cosmological model which may provide hints as to what could happen for real gases.It can be viewed as a one-dimensional version of the Born-Infeld system;that is,a nonlinear modification of the Maxwell equations for solving the electrostatic divergence generated by point particles in classical electrodynamics.One remarkable feature of this dynamics is that the characteristic fields are linearly degenerate.More about its physical backgrounds can be found in[1,13]and the references therein.
The initial data are

On the Cauchy problem with large initial data in thespace,the degenerate systems differ significantly with the genuinely nonlinear systems or linear systems.For example,the Riemann solution of Chaplygin gas dynamics has the property,shared with some non-strictly hyperbolic conservation laws[21],that for certain Riemann initial data Uland Ur,either of their small variations could result in extreme changes in the intermediate states.In other words,concentrations of mass(Dirac singularity of density)called δ-shocks may form for certain initial data,and this corresponds to the case of overlaps of the two families of characteristics[7,18].However,this will not happen to polytropic gases p=A0ργwith γ the adiabatic exponent,as the two characteristic fields are genuinely nonlinear.Neither will this happen for the linear equations.
For polytropic gases,for when=1(that is,for an isothermal gas),Nishida[27]obtained the BV solutions excluding vacuum for(1.1)with large initial data in the BV space by the random choice method,Huang and Wang[20]obtained the L∞solutions that may include a vacuum by a compensated compactness and analytic extension theorem,while LeFloch and Shelukhin[22]achieved it by compensated compactness arguments and symmetry group analysis.For when γ>1,the existence of L∞solutions for different γ were obtained by DiPerna[16],Ding,Chen and Luo[14,15],Chen[12],Lions,Perthame,and Tadmor[25],Lions,Perthame,and Souganidis[24].Chen and LeFloch explored the L∞entropy solution for general pressure in[11].See[2,8,9]for more on the global uniqueness and the stability for general systems.
For Chaplygin gas dynamics,the existence of a solution to the Cauchy problem with large initial data in the L∞space was obtained in[10],by the method of quasi-decoupling,provided that the initial density is bounded and bounded away from a vacuum;see also[28]for an explicit solution.For smooth or L∞initial data,the solutions are as regular as the initial data,due to the degeneracy of the system([28,30]);see also[17,29]for more studies on this kind of system.
As far as we know,no research on the Cauchy problem of the Euler system(1.1)with large initial data in the L1space has been performed.
For pressureless flow,another typical known degenerate and non-strictly hyperbolic 2×2 system and the well-posedness of its Cauchy problem has been obtained with general initial data being of Radon measure.Compared to that non-strict hyperbolicity,system(1.1)for a Chaplygin gas is strictly hyperbolic in the domain away from a vacuum.This difference means that one can hardly use the generalized variational principles as in[19].We prove the existence of a solution by Lagrangian representation,and a property about the Newton-Leibniz formula on monotone functions.The novelty,and also the essence of the difficulty of this paper,lies in that there is no assumption on the local boundedness of the initial density in the wellposedness of the Cauchy problem of the Euler system.Neither the method of compensated compactness nor that of quasi-decoupling can be applied without some changes,including some possible approximation to the local L1norm of the initial data.This in turn may require the establishment of another new compactness frame.The second contribution of this paper is that we make use of the method of Lagrangian representation to obtain not only the global existence and uniqueness of the Cauchy problem with large initial data in thespace,but also the regularity of the solution for the degenerate system.
More on the method of Lagrangian representation in research on the regularity of scalar conservation laws and systems with bounded and continuous initial data can be found in[3,4,6,26]and the references therein.In these works,the existence of Lagrangian representation was obtained essentially by a wave-front tracking approximation scheme.
We prove the existence of the Lagrangian representation by using the Radon-Nikodym Theorem,as well as the property on monotonic functions mentioned above.More precisely,we first establish the relationship between a time-space point and the Lagrangian representation through conservation laws(1.1).Then,by Radon-Nikodym Theorem and detailed analysis,we obtain the unique existence of Lagrangian representation.
The weak solution is defined as follows:

and(ρ(x,t),u(x,t))|t=0=(ρ0(x),u0(x))a.e..
Our main result is stated as follows:
Theorem 1.2Assume the initial data(ρ0,u0)are measurable and satisfy that

Then the Cauchy problem of the Chaplygin gas(1.1)(1.2)admits a unique global weak solution(ρ,u)satisfying that
The remainder of the paper is organized as follows:in Section 2,under the assumptions in Theorem 1.2 on the initial data,we get the existence of the dependent interval at t=0 for any given point(x,t)in the upper half plane through two crucial integral equations,so that we can get the Lagrangian representation of a weak solution.Some regularity properties of these are given.In Section 3,we define two functions via the result obtained in Section 2 and focus on proving that they are the derivatives of two absolutely continuous potential functions,so that are the solution in search.The regularity of the solution is then studied,and some analysis is performed on its characteristics and streamlines.In Section 4,by construction,we show that the characteristics of the solution should satisfy the integral equations.Then,by the uniqueness of the solution to the integral equations,we conclude that the solution of system(1.1)is unique.Combining the lemmas in Sections 2 and 3,we get the conclusion stated in Theorem 1.2,and thus complete the proof.We give some discussion in Section 5.During the proofs of the existence of Lagrangian representation and the absolutely continuity of the potential functions,we use a fact about monotonic function that gives a sufficient and necessary condition for distinguishing those monotonic functions satisfying the fundamental theorem of calculus for Lebesgue integration.The proof of the lemma is given in the appendix.
2 Determination of the Lagrangian Representation
The classical characteristic analysis of mass and momentum potentials gives the relationship between a space-time point(x,t)and its dependent interval with endpoints(ξ,0)and(η,0)as follows:

and(ξ,η)|t=0=(x,x).
Hereafter,ρ0,u0are supposed to satisfy the assumptions proposed in Theorem 1.2,and hence system(2.1)is well-defined.This is crucial to our search for a low regular solution.The pair ξ=ξ(x,t)and η=η(x,t)satisfying(2.1)are called a Lagrangian representation of an entropy solution(ρ,u)if they are the generalized characteristics via(x,t)and Lipschitz with respect to t,increasing with respect to x.One can refer to[4–6,26]and the references therein for more versions.We have the following existence result regarding(ξ,η):
Lemma 2.1Under the assumptions(i)–(iii)in Theorem 1.2,system(2.1)admits a unique solution(ξ,η)for any given(x,t).
ProofLet m0(x):=It follows that m0(x)is strictly increasing and absolutely continuous with respect to x in view of the Radon-Nikodym Theorem,and m0is a measure on R satisfying
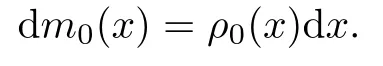
Then(2.1)1can be reduced to

Obviously,η<ξ for any t>0.In view of the strict monotonicity of m0and the assumption(i)in Theorem 1.2,one can solve,from(2.2),the value of η as a function of(ξ,t)as follows:

Moreover,η is strictly increasing with respect to ξ for fixed t.
Now,to get the existence of(ξ,η),it is enough to establish a homeomorphism between ξ and x for each fixed t>0.
First of all,(2.1)2gives an injection from x to ξ.In fact,from(2.2),we have that
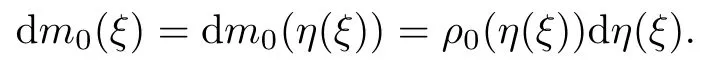
Then,by(2.3),we have that

Since

(2.1)2can be written as

In view of(2.4),one can reduce(2.5)to

Noting that the second integral on the left hand side of(2.6)is independent of x,we just need to consider the first integral on the left.Since η<ξ,it follows by(2.3)and the assumption(iii)in Theorem 1.2 that w0(s)>Then(2.6)implies that ξ is strictly increasing with respect to x.
Next,we discuss the mapping defined by(2.1)2from x to ξ.Indeed,making use of(2.5)we can rewrite(2.1)2as follows:

Consider the two terms on the left side of(2.7).For the first term,it holds that
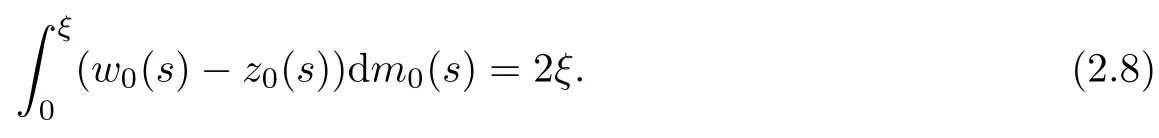
For the second one,we have,for fixed ξ0and ξ<ξ0,the following:

Thanks to(2.2),we have
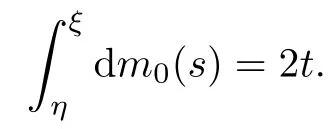
Thus,(2.9)is reduced to

Then,(2.7),together with(2.8)and(2.10),implies that x goes to?∞as ξ goes to?∞.
On the other hand,one could also rewrite(2.1)2in the following form:

Similarly to(2.8),and from(2.3),we have

while for η>ξ0,it holds that

Then it follows from(2.11),(2.13)and(2.12)that x goes to+∞as ξ goes to+∞.
The proof of this lemma is complete. □
To characterize the regularity property of ξ(x,t)and η(x,t),and for the later use of proving the existence of a weak solution,we need the next lemma.This gives a sufficient and necessary condition to distinguish those monotonic functions satisfying the fundamental theorem of calculus for Lebesgue integration;in other words,those that are absolutely continuous are given in the Appendix.
Lemma 2.2Assume that g(x)is a strictly monotonic continuous function defined on[a,b]and that the functiondefined on g([a,b])satisfies g((y))=y for any y∈g([a,b]).Then g is absolutely continuous if and only if the Lebesgue measure of the set on which the derivative ofvanishes is zero.
We proceed this lemma to prove the following result:
Lemma 2.3Both ξ and η are continuous functions of(x,t).They are strictly increasing and absolutely continuous with respect to x for any fixed positive t.For fixed x,ξ(x,t)(resp.η(x,t))is a strictly monotonic and absolutely continuous function of t on any interval[a,b]with a
ProofConsider the continuity of ξ and η.Suppose,to the contrary,that(ξ,η)is discontinuous at some point(x0,t0).Then there is a sequence(xn,tn)converging to(x0,t0)as n→∞and a corresponding sequence(ξn,ηn)such that either any subsequence of{(ξn,ηn)}does not converge,or there is a subsequence of it denoted still by them such that limn→+∞(ξn,ηn)/=(ξ0,η0).
Now(2.1)2,or,equivalently we have(2.11);that is

so we have
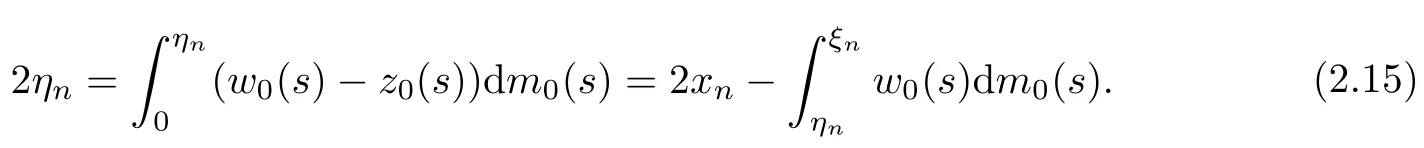
Let ξ0be a Lebesgue point of z0.We claim ηn≤ξ0or ηn≤xn?z0(ξ0)tn.Then,from the uniform boundedness of xnand tn,we conclude that ηnand so ξnis upper bounded.In fact,if ηn≥ξ0,then

we have

Letting ξ1be a Lebesgue of z0,we have either ξn>ξ1or ξn≥xn?w0(ξ1)tn.This gives the lower boundedness of ξn,and then that of ηn.
Therefore,{(ξn,ηn)}are uniformly bounded,and thus there should exist a subsequence denoted still by(ξn,ηn)that converges to a pointHowever,by(2.15)and(2.17)we know thatshould coincide with(ξ,η)(x0,t0),due to the uniqueness of(2.1)obtained by Lemma 2.1.
The assertions on the monotonic property of ξ and η with respect to x follow from the fact that ξ(x,t)(resp.η(ξ))is strictly increasing with respect to x(resp.ξ)as indicated in(2.6)in Lemma 2.1.

The part of t can be obtained by contradiction.If there is some x0∈R such that ξ(x0,t)is not strictly monotonic with respect to t on[a,b],then there exist ti∈R×[a,b](i=1,2,t1>t2)and a corresponding(ξi,ηi)satisfying(2.1)with ξ1=ξ2.The subtraction of these two pairs in(2.1)2gives Now the left part of(2.18)is zero,since ξ1=ξ2,while z0is sign-preserved on η(x0,[a,b]).Then we have η1=η2,which is impossible in view of t1/=t2and(2.1).Thus,ξ(x,t)is strictly monotonic with respect to t on[a,b].Conversely,t is also a strictly monotonic function of ξ,and is differentiable almost everywhere.Thus,we have

Similar arguments also can be applied to the case,w0(ξ(x,t))<0 or w0(ξ(x,t))>0 a.e.on[a,b],to get the conclusion on η(x,t).
The proof of this lemma is complete. □
Remark 2.4We can see from(2.2)that for fixed η,the solvability of ξ requires the infinity of m0(ξ)as t goes to±∞.This indicates that the assumption “for any constants a and b∈R”is essential to the solvability of(ξ,η)of(2.1).
3 Existence of Weak Solution
We will prove the existence of a solution by the notion of Lagrangian representation.By Lemma 2.1,system(2.1)determines two functions:ξ=ξ(x,t),η=η(x,t).
Define the density and velocity as follows:

Naturally,by the assumption(iii)of Theorem 1.2,we have that ρ(x,t)>0 a.e..In view of(ξ(x,t),η(x,t))|t=0=(x,x),we have

In addition,we have
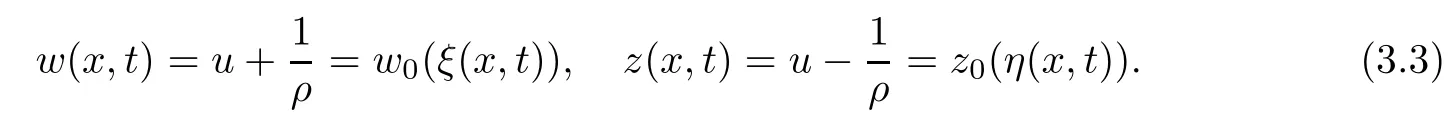
Define

Obviously,

By direct calculations,we formally have that

as well as

To prove that(3.1)is exactly the weak solution of(1.1)and(1.2),it is enough to show thatandare absolutely continuous functions of x and t.
By Lemma 2.3 we know that ξ(x,t)and η(x,t)are absolutely continuous with respect to x for fixed t.Then,by(3.4)and(3.5),we know that both(x,t)and(x,t)are absolutely continuous functions of x for fixed t.
Next,we focus on the absolute continuation ofandwith respect to t for fixed x.In fact,as mentioned in Section 3,it is easy to get the result if w0(ξ)<0 or z0(η)>0.While based on the assumptions on initial data,we will divide the discussion on w0(x)into the following two cases:
Case(1) there is a sequence xn→+∞which are Lebesgue points of w0such that w0(xn)≤0;
Case(2) there is a Lebesgue point x0of w0such that w0(x)>0 a.e.for x>x0.
We analyze the absolute continuation ofandwith respect to t for each case in the sequel.

Case(2)There is a Lebesgue point x0of w0such that w0(x)>0 a.e.for x>x0.We divide this case into two subcases.
Subcase a):w0(x)>0 a.e..In this case,by Lemma 2.3,η is an absolutely continuous function of t.Thus,by Lemma 2.3,(3.4),(3.5)and(2.1),we know that both(x,t)and(x,t)are absolutely continuous functions of t.
Subcase b):There is a Lebesgue point x0of w0such that w0(x0)≤0,while w0(x)>0 a.e.for x>x0.This subcase is divided into four cases:
Case(i):z0(η(x,t))<0 a.e.for t>0;
Case(ii):there is a t1>0 such that z0(η(x,t))<0 a.e.for t Case(iii):z0(η(x,t))≥0 a.e.for t>0; Case(iv):there is a t1>0 such that z0(η(x,t))≥0 a.e.for t We analyze these one by one. Case(i):If z0(η(x,t))<0 a.e.for t>0,then by the argument in Case(1)we know that both(x,t)and(x,t)are absolutely continuous functions of t. Case(ii):If there is a t1>0 such that z0(η(x,t))<0 a.e.for t Now we focus on the part where t>t1.In view of z0(y) Case(iii):If z0(η(x,t))≥0 a.e.for t>0,the absolute continuation of(x,t)and(x,t)with respect to t follows from Subcase a),since w0(ξ(x,t))>z0(η(x,t))a.e.implies that w0(ξ(x,t))>0 a.e.. Case(iv):There is a t1>0 such that z0(η(x,t))≥0 if t Therefore,we arrive at the following conclusion: Lemma 3.1Both(x,t)and(x,t)are respectively absolutely continuous functions of x and t for all t>0,and(3.7)–(3.10)holds. Now we proceed to prove that(ρ,u)satisfies system(1.1)in the sense of distribution. Lemma 3.2The pair(ρ,u)given by(3.1)satisfy(1.3). ProofIn view of Lemma 3.1,it(3.7)–(3.10)holds.For anywe have Thus,(ρ,u)satisfies the first equation of(1.3). The same argument gives the second equation of(1.3).Thus the proof of this lemma is complete. □ In the following,we will prove that the solution ρ,u defined in(3.1)has the regularity properties(1)–(3)of Theorem 1.2: Lemma 3.3The quantities ρ,u defined in(3.1)satisfy the following: due to the assumption(ii)in Theorem 1.2. Similarly to(3.15)and(3.16)regarding v1,we get The addition of(3.16)and(3.17)gives the local L1integral of ρ(x,t)u2(x,t),1ρ(x,t).While the subtraction of(3.16)and(3.17)gives the local L1integral of u(x,t). Due to assumption(i)in Theorem 1.2,we have The proof of this lemma is complete. □ Next,we depict the characteristics of system(1.1).As above,(ξ,η)=(ξ,η)(x,t)is determined by(2.1).We have Lemma 3.4For any given ξ0∈R,ξ(x,t)=ξ0determines a backward characteristic satisfying Meanwhile,η(x,t)=η0with η0a constant determines a forward characteristic satisfying Both characteristics are absolutely continuous functions of t. ProofFor ξ=ξ0,(2.3)determines a function η=η(t;ξ0).Then,by(2.1)2,we have that which determines a mapping from t to x,denoted by x(t;ξ0).Since it follows from(3.22)that In view of(2.2),we have that For η=η0,similarly to ξ=ξ0,there exists ξ(t;η0)and then x(t,η0)such that(2.1)holds,that is, Thus, Equipped with the information on characteristics,we can determine the streamline via each point in the upper half(x,t)plane. Suppose that(ρ,u)are weak solutions of(1.1)satisfying(1)-(4)of Theorem 1.2.Then,for any Lebesgue point(x,t),we still denote the endpoints of its dependent interval by(ξ,0)and(η,0).We claim that(x,t)and(ξ,η)should satisfy(2.1). This implies that x=x1(t)is indeed the first family of characteristics. □ Lemma 4.2Suppose ρ,u are weak solutions of the Cauchy problem(1.1)(1.2).Then for any given point(x,t)in the upper half plane,the two abscissae of the two families of characteristics via(x,t)that intersect with the x-axis should satisfy(2.1). ProofFor any x∈R,in the domain bounded by x=x,x=x0(t),t=t1and t=t2,by the conservation law of momentum,we have for t2>t1>0 that Then,by(4.5),we have that Noting that with(ξ,η)|t=0=(x,x). □ Proof of Theorem 1.2The existence of a solution to the Cauchy problem(1.1)(1.2)follows from Lemma 3.2 and(3.2). Remark 4.3The assumption(iii)in Theorem 1.2 is necessary to rule out the Dirac measure singularity.In fact,writing system(1.1)in Lagrangian coordinates,we have Remark 4.4The unique solution(ρ,u)is given by(3.1),up to a set of zero measure with Hausdorffdimension 1. By Theorem 1.2,Definition 1.1,Remarks 2.4,4.3 and 4.4,we know that the conditions proposed on the initial data in Theorem 1.2 are sufficient and also necessary for the equivalence of Chaplygin gas dynamics in Eulerian and Lagrangian coordinates[32].This result generalizes and develops the previous ones on a weak solution to a typical system of conservation laws whose characteristics are linearly degenerate.This should be helpful for further study on more general linearly degenerate systems.For initial data that are of Radon measure as in[19],the well-posedness of this system is still open. Appendix Proof of Lemma 2.2Without loss of generality,we assume that g is an increasing function. 1.Necessity.If g is absolutely continuous,we show that the Lebesque measure of keris zero.To achieve this,we need a known result[33,p274 Theorem 5.25],as follows: Assume that g(x)is differential almost everywhere on[a,b],that f(x)is integral on[c,d],and that g([a,b])?[c,d].Denote Then the following two propositions are equivalent: (1)F(g(t))is absolutely continuous on[a,b]; (2)f(g(t))g′(t)is integral on[a,b]and Therefore,we have that Thus g is absolutely continuous.The proof of this lemma is complete. □





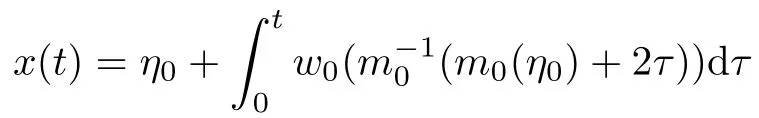

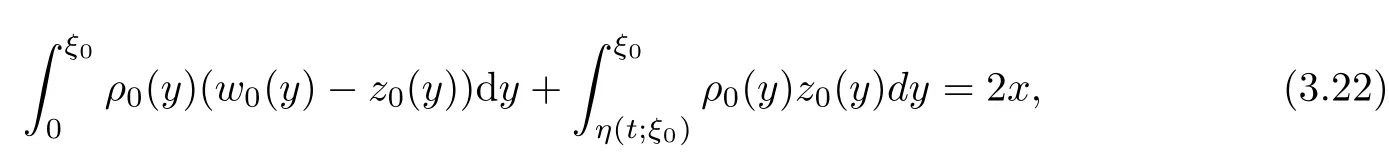






4 Uniqueness







5 Some Discussion




 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
