BILINEAR SPECTRAL MULTIPLIERS ON HEISENBERG GROUPS?
(宋乃琪)
Key Laboratory of Mathematics and Complex Systems,Ministry of Education,Institution of Mathematics and Mathematical Education,School of Mathematical Sciences,Beijing Normal University,Beijing 100875,China
School of Chinese Medicine,Beijing University of Chinese Medicine,Beijing 100029,China
E-mail:songnaiqi2007@126.com
Heping LIU(劉和平)
School of Mathematical Sciences,Peking University,Beijing 100871,China
E-mail:hpliu@math.pku.edu.cn
Jiman ZHAO(趙紀滿)?
Key Laboratory of Mathematics and Complex Systems,Ministry of Education,Institution of Mathematics and Mathematical Education,School of Mathematical Sciences,Beijing Normal University,Beijing 100875,China
E-mail:jzhao@bnu.edu.cn
Abstract As we know,thus far,there has appeared no definition of bilinear spectral multipliers on Heisenberg groups.In this article,we present one reasonable definition of bilinear spectral multipliers on Heisenberg groups and investigate its boundedness.We find some restrained conditions to separately ensure its boundedness from C0(Hn)×L2(Hn)to L2(Hn),from L2(Hn)×C0(Hn)to L2(Hn),and from Lp×Lq to Lr with 2 Key words Bilinear spectral multipliers;Heisenberg groups;boundedness Study of the multiplier theorem can be traced back to 1939,at the work of Marcinkiewicz[36].Afterwards,plenty of works focussing on studying the boundedness of Fourier multipliers appeared(see,for example,[3,5,10,24,26–28,32,35,41,42,47,49–52]). Ideas about the multilinear multipliers on Rnoriginated in the remarkable work of Coifman and Meyer[11–13]and have been well studied by many authors(see,for example,[24,26–28,42,47,49]).For the sake of simplicity,we recall the bilinear case.The bilinear Fourier multipliers on Rnhave the form (where N is strictly larger than 4n). On the other hand,by using the bilinear T1 theorem in the sense of Grafakos and Torres([29]),condition(1.1)with N=2n+1 assures the boundedness of Tm. Tomita proved a H?rmander type theorem for bilinear Fourier multipliers,and consequently weakened the regular assumptions([47]).For m∈L∞(R2n),set mk(ξ,η)=m(2kξ,2kη)Ψ(ξ,η),where(ξ,η)∈Rn×Rn,k∈Z,and Ψ∈S(R2n)satisfies The topic of multipliers on Heisenberg groups is also interesting.There are several works about linear cases,including spectral multipliers and Fourier multipliers.Studies on the multilinear cases have not appeared as yet. The spectral multipliers on Heisenberg groups are related to sub-Laplacian operators on Heisenberg groups.Michele and Mauceri([39])considered the spectral multipliers on stratified groups which contain Heisenberg groups.Letting L be the sub-laplacian operators on stratified groups and N the homogeneous dimension of stratified groups,then spectral multipliers have the form In 1994 and 1995,Hebisch and Zienkiewicz([30,31])and Stein and Müller([43]),respectively,found that the condition of the boundedness of spectral multipliers could be weaker on the Heisenberg groups.They replaced the homogeneous dimension with a topological dimension;that is,the result holds when s The Fourier multipliers on Heisenberg groups first appeared in the paper of Michele and Mauceri.In their paper,the definition of Fourier multipliers is very different from that which is in Rn.Their multiplier is an operator valued function on Heisenberg groups,bounded from Lpto Lpfor p>1 and bounded from L1to L1,∞(for details,see[40]). In addition,there are many other studies about spectral multipliers on abstract spaces such as[1,6,7,9,14,22,33,37,44,48]etc.. There are,however,no results about multilinear spectral multipliers and multilinear Fourier multipliers on Heisenberg groups,even in terms of their definitions.In this article,we will give a reasonable definition of bilinear spectral multipliers,and prove its boundedness under some restrained conditions.Our definition of the bilinear spectral multipliers is given by Definition 1.1Let m(λ1,λ2)∈L∞(R+×R+).Then bilinear spectral multipliers Tm(f,g)(x)have the form For the definitions of Pλ,dμ(λ),see Section 3. Now we state the main results of our paper.First,we have the following: Theorem 1.2s≥3N+6.If m(λ1,λ2)satisfies suppm(λ1,λ2)?{(λ1,λ2):0≤λ2≤2?2M1?3λ1}and for any s1+s2≤s,then Moreover, Accordingly,we have Theorem 1.3s≥3N+6.If m(λ1,λ2)satisfies suppm(λ1,λ2)?{(λ1,λ2):0≤λ1≤}and for any s1+s2≤s,then we have Moreover, The meaning of constant M1will be explained in Section 2. Furthermore,we have the following conclusion: Moreover, This paper is organized as follows:in Section 2,we give some basic concepts and notations,including properties of some useful Harmonic analysis tools on Heisenberg groups.In Section 3,we define the bilinear spectral multipliers and prove their boundedness. In this chapter,we give some basic definitions and properties on Heisenberg groups which could be found in[4,18,19,21,34]. Let Hn=Cn×R be Heisenberg groups.Their group law has the form For any r>0,we have Let gLand gRbe the left invariant vector fields and right invariant vector fields,respectively,on the Heisenberg groups.Denote by X1,...,X2n+1a basis of gL,and Y1,...,Y2n+1a basis of gR.For f∈C1(Hn),we have Observe the following two facts about Heisenberg groups([19],Proposition 1.6,Lemma 1.10): The following theorems are very useful([19],Proposition 1.33): Theorem 2.1There exist C>0 and β≥1 such that,for all f∈C1(Hn)and x,y∈Hn,we have Theorem 2.2There exist C>0 and β≥1 such that,for all f∈C1(Hn)and x,y∈Hn,we have The convolution on Heisenberg groups is defined by and this satisfies The sub-Laplacian operator on Heisenberg groups is defined by The Schwartz seminorm on Heisenberg groups is defined by S(Hn)denotes Schwartz function spaces. Letting e?Lf=f?hheat(x),we have([19],Proposition 1.74) The following theorem gives a condition sufficient to show that the kernel of m(L)belongs to Schwartz function spaces: Theorem 2.3(See[20],Corollary 7) Let m be the restrictions of m0(m0∈S(R))on R+.Then the kernel of operator m(L)(denoted by M)satisfies M∈S(Hn). For operator m(L),which is well-defined,we have Now we introduce the Bergmann representation on Heisenberg groups(see[21]).Denoting by Hλthe Bergmann-Fock space(λ∈R{0}),its definition is given by where the norm of Hλis defined by The corresponding irreducible unitary representation uλof the group Hnis realized on Hλ(Cn)by Then the group Fourier transform is given as follows: Definition 2.4(See[21]) Let f∈L1(Hn).Then the Fourier transform of f is the operator on Hλ(Cn)parametrized by λ∈R{0}defined by Recall that an operator A(λ)of Hλsuch that For any f∈L2(Hn),we have the following Plancherel formula([2],Theorem 1): Theorem 2.6 Regarding the sub-Laplacian operator([2],Page 20,1.2.28-1.2.29),we conclude that According to the spectral theorem,we could define the operator m(L)for any bounded Borel function m on[0,+∞),and get The Fourier transform of convolution satisfies Let C00={τ∈R:The following theorem shows that the Fourier transform of the product of two functions is localized whenever each of the Fourier transforms of two functions is localized: Lemma 2.7(See[21]) There is a constant M1∈N such that,if we consider f and g to be two functions of S(Hn)satisfying If u is a locally integrable function on G and B is a ball on G,we set Then define BMO(“bounded mean oscillation”)as the space of all locally integrable functions u on G(see[19])such that If f∈S′and φ∈S,the nontangential maximal function Mφf is defined by Theorem 2.8([19],Theorem 2.4) λ>N.Let Aλbe the set of all the measurable functions φ which satisfy|φ(x)|≤(1+|x|)?λon Hn(absolutely we have Aλ?Lq,1≤q≤∞).If f∈Lp(Hn)(1 for every λ>N there exists a constant Cλsuch that For m∈L∞(R+),the spectral multipliers on Heisenberg groups have the form We define the bilinear spectral multipliers on Heisenberg groups as follows: Definition 3.1Let m(λ1,λ2)∈L∞(R+×R+).Then bilinear spectral multipliers Tm(f,g)(x)have the form Now we prove the boundedness of bilinear spectral multipliers. First we consider the case when suppm(λ1,λ2)?{(λ1,λ2):0≤λ2≤}.We have the following conclusion: Theorem 3.2s≥3N+6.If m(λ1,λ2)satisfies for any s1+s2≤s,then Moreover, ProofLet f,g∈S(Hn).Choose ψ∈S(R+)and suppψWith the range of ψ?[0,1],for any λ∈R+,ψ satisfies Thus we get(3.2).Consequently,we have The bilinear spectral multipliers could be written as Now we give some useful Lemmas. Lemma 3.3([39],Lemma 3.1) For El1(x),we have the following estimate: The last inequality above is obtained by(3.4).We can get the following in a similar way: If we let M=0,then we have ProofFirst,we have The two lemmas below are useful in the proof of our main results. where Q denotes a ball on Hnand T(Q)=Q×[0,rQ]. ProofAccording to the definition of measureμ,for everyμ-measurable function F that is defined on Hn×(0,+∞),we have We pick a ball Q on Hn,and let Q?and Q be at the same centre and let rQ?=(2γ+1)rQ.We let F be a characteristic function on T(Q),and we split f as follows: where Then,according to the Plancherel formula(see(2.7)), In the last inequality above,we used two following facts(their proofs are similar to the cases in Rn;see[23],Corollary 7.1.8;Proposition 7.1.5): we have that Then we combine(3.10)with(3.11),and we can get The last inequality above comes from the following result(its proof is similar to Rn(see[23],Proposition 7.1.5)):for any δ>0 and any ball B(x0,R)on Hn,we have Hence the result is Lemma 3.7There exists a constant CNrelated to the group dimension such that for any α>0,and all the measuresμ≥0 on Hn×(0,∞),and allμ-measurable functions F on Hn×(0,∞),we have Then we can get where L∈N is a constant and any point in ?αfalls into at most L balls of T2Qk(∪kT2Qk??α,1 According to Lemma 3.7,it is easy to find that Now we return to the proof of our main result.We know that Then we consider For M,N∈Z+,we have We define function F(x,s)on Hn×(0,∞)as follows: According to Lemma 3.6,(3.12)and(3.13)we have We can deduce F?(x)=(x)from the definition of F?(see Lemma 3.7)and the definition of a nontangential maximal function(see 2.10).Because of Lemma 3.4 and(3.6), and combining this with the property of the maximal function(Theorem 2.8),we have Now we have This means that for any given ε>0,there exists N0>0 such that From the proof above we know that and since S(Hn)is dense in C0(Hn)in the L∞norm,we obtain our conclusion. □ Similarly,we have the following: Theorem 3.8s≥3N+6.If suppm(λ1,λ2)?{(λ1,λ2):0≤λ1≤}and satisfies for all s1+s2≤s,then we have Moreover, ProofThe proof is similar to that of Theorem 3.2. □ In this section,we first give some results about vector-valued singular integrals on homogeneous spaces([25]).These results could be used in the discussion of bilinear spectral multipliers on Heisenberg groups.We denote by X an homogeneous space,satisfying a doubling measure condition.Let B1,B2be two Banach spaces.We consider the kernel(x,y)defined on(X×X)△(△={(x,x):x∈X}),and say that the kernel(x,y)∈L(B1,B2)(L(B1,B2)denotes the bounded linear operators from B1to B2).We denote bythe norm of(x,y)in L(B1,B2). Notice that Hnis also an homogeneous space. We call the two conditions that follow H?rmander conditions of kernel.There exists a constant CHsuch that,for all y,z∈X, and for all x,ω∈X, We have the following lemma: Lemma 3.9([25],Theorem 1.1) Let B1and B2be two Banach spaces.If there exists r∈(1,∞]such that the operatoris a bounded linear operator from Lr(X,B1)to Lr(X,B2),its norm is Ar>0,andsatisfies the H?rmander conditions.Then the definition ofcan be expanded to Lp(X,B1),p∈[1,∞).Furthermore,there exist two positive constants CX,C?X,such that,for all F∈L1(X,B1), and for all F∈Lp(X,B1),p∈(1,∞), where Cp=max(p,(p?1)?1).When r=∞,the results also hold with Cp=max(1,(p?1)?1). Remark 3.10Notice that if we let d(x,y)≥2γ2(1+β)d(y,z)and d(x,y)>2γ2(1+β)d(x,ω)(γ,β≥1,see(2.1),Theorem 2.1,Theorem 2.2)in(3.20)and(3.21),and then repeat the proof of Lemma 3.9,the results also hold. Theorem 3.11s≥N+5.If suppm(λ1,λ2)(N0∈N+)and m(λ1,λ2)satisfies for all s1+s2≤s,then Moreover, ProofIn the proof of this theorem,we set function∈S(R+)and satisfy following conditions: By the Plancherel theorem(see(2.7)),we have Now we consider Z For|y?1x|≥2γ2(1+β)|y?1z|,by the mean value theorem(see Theorem 2.1,Theorem 2.2),we have Now we explain how to get the third inequality above.First, Due to|y?1x|≥2γ2(1+β)|y?1z|,we have that Thus|ω2j(z?1x)|≥γ?1|2j?1(y?1x)|,and we get the third inequality. (3.24)means that We also have that We take geometric average for(3.24)and(3.26)to get Therefore,we can get Similarly,we can get According to Lemma 3.9,we know thatis a bounded linear operator from Lp(Hn,C)to Lp(Hn,?2)and satisfies We also can prove the following in the same way: The proof of the inequality above is similar to that of Rn(see[15]). Taking the Lrnorm,we have Notice that p,q>2.Since(the proof is similar to Rn,see[17]) and in accordance with(3.28)and(3.29),we have We consider the constant Chas follows: For any α,β≥0,we can get Since combined with the fact that(λ1,λ2)∈[2?N0,2N0]×[2?3N0,23N0],we have that holds for all j. Analogous to the discussion of the previous case(see(3.2)),we know that Then Denote by[·]a step function,we have that1 Introduction
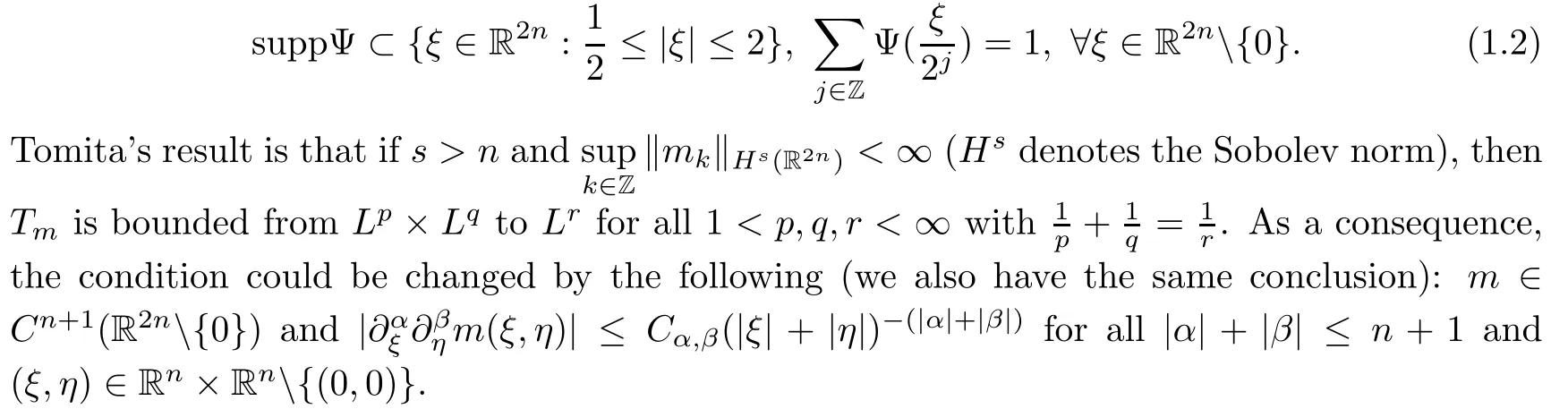

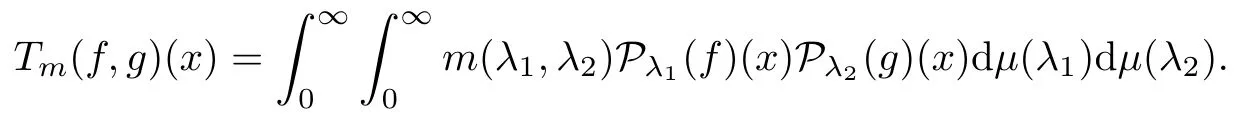
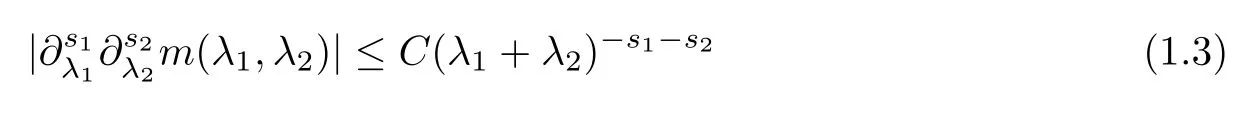
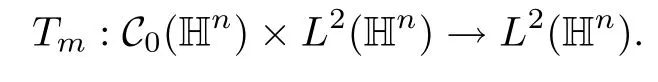
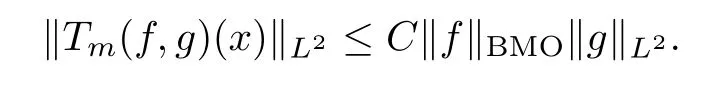
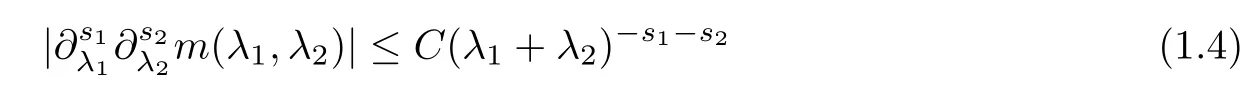
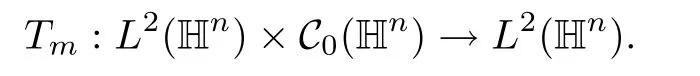
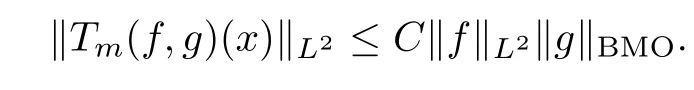
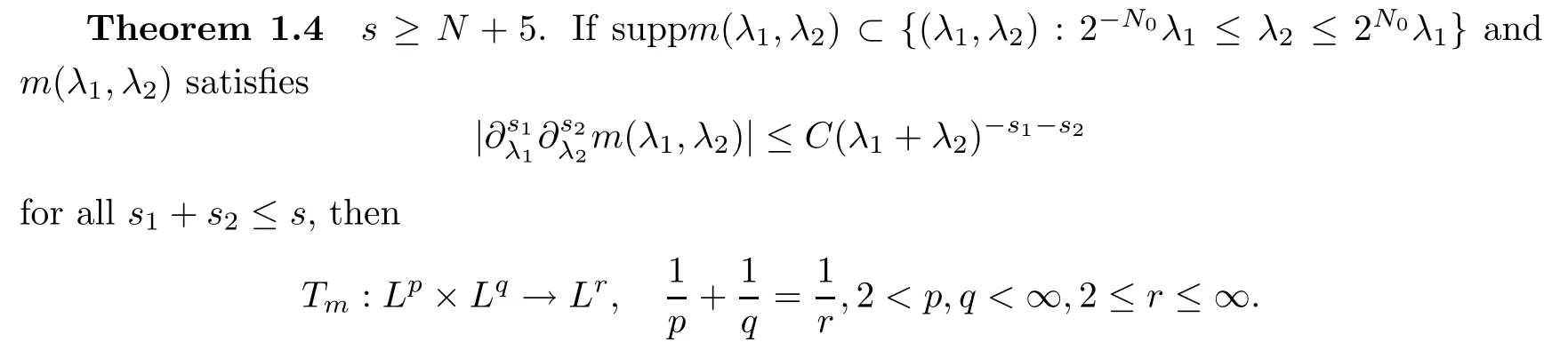
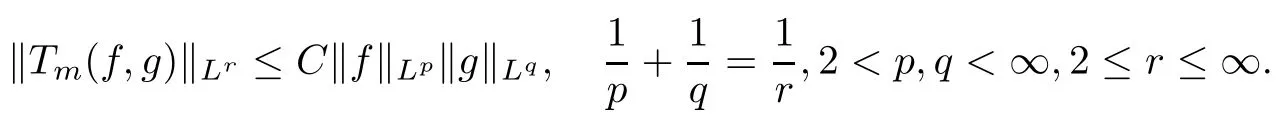
2 Preliminaries
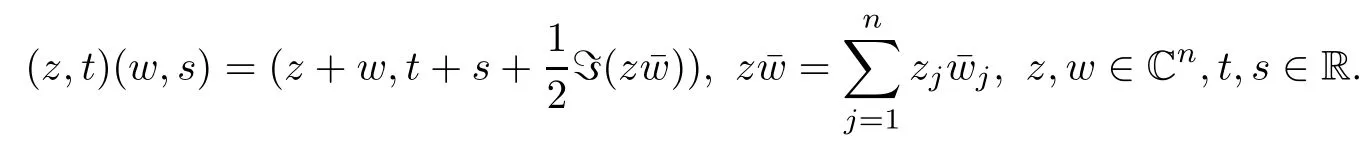
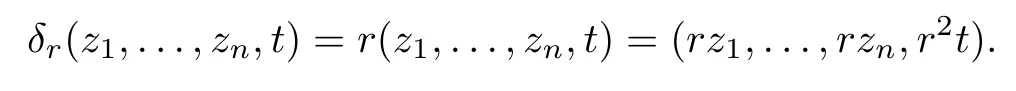
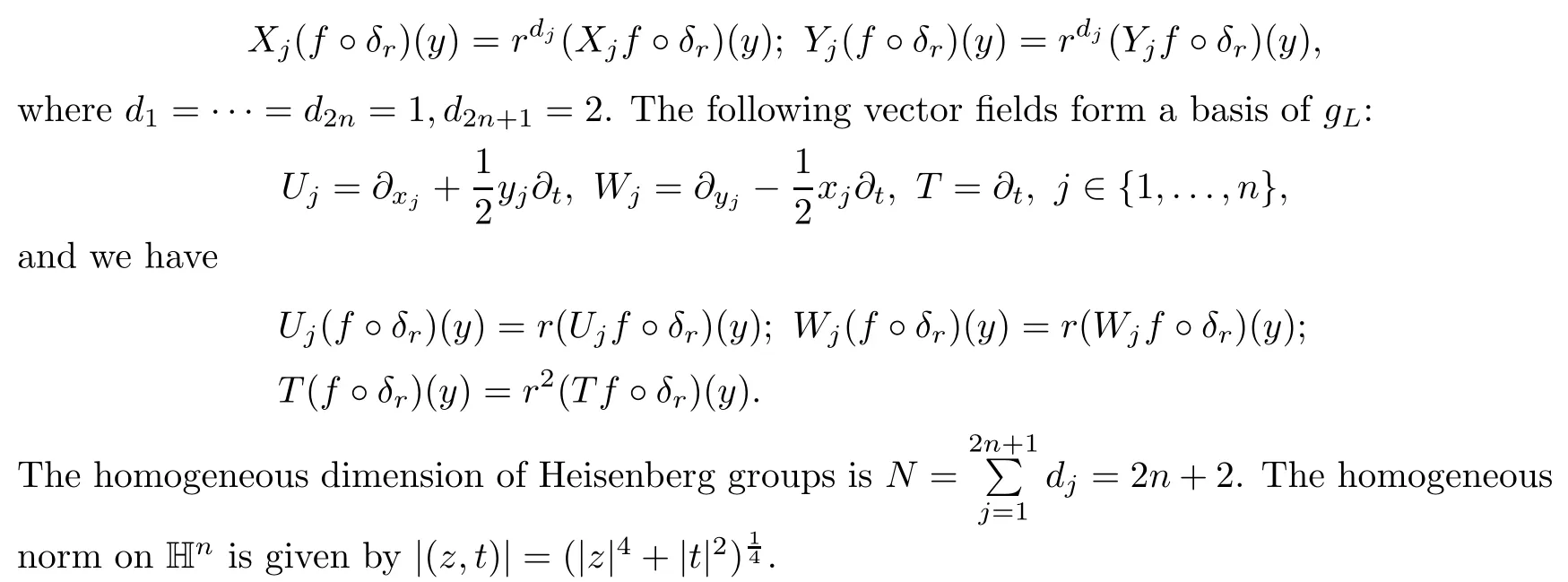

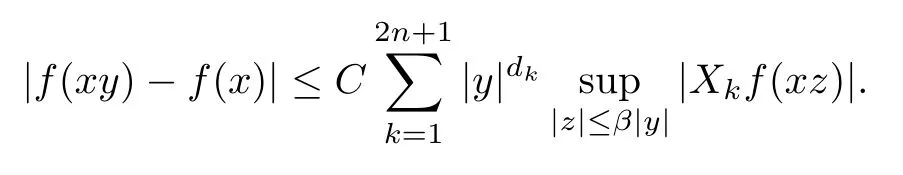
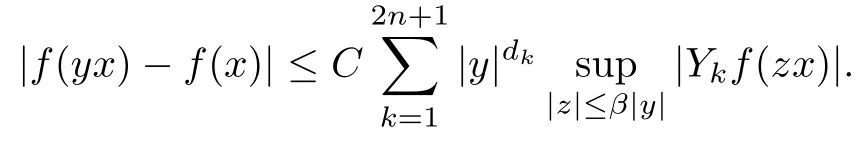
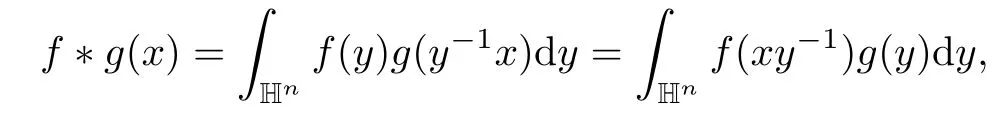


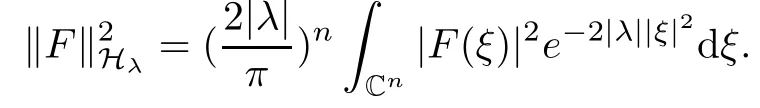

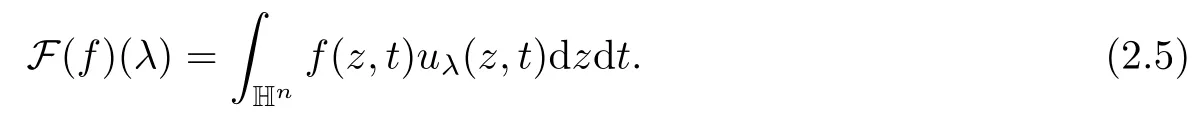
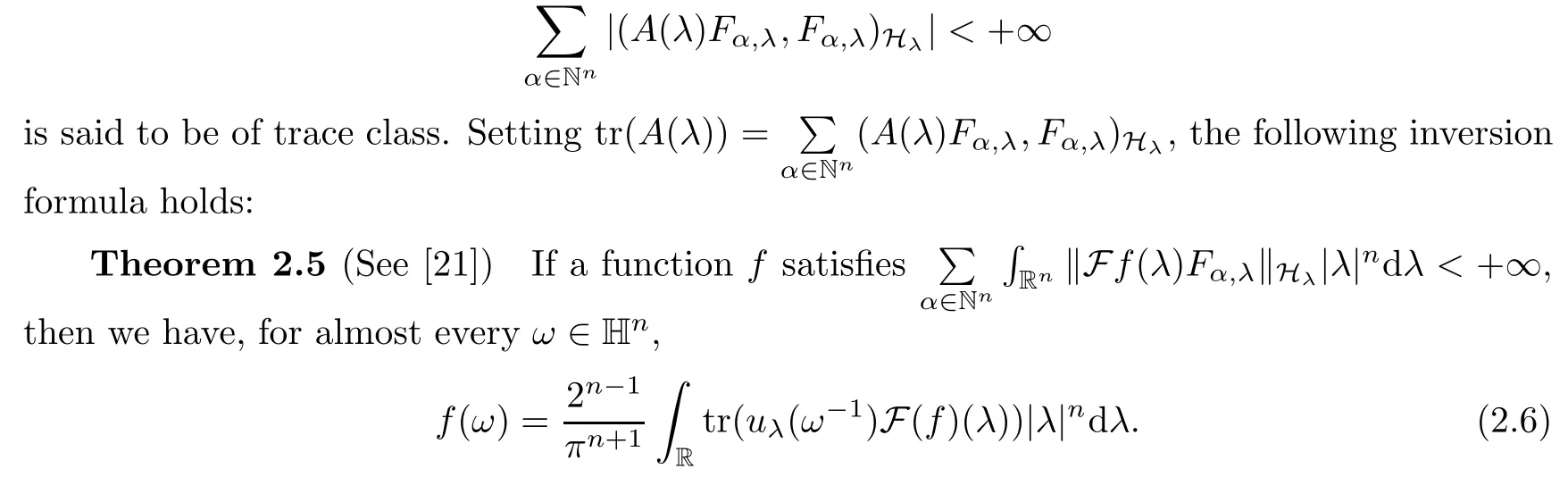
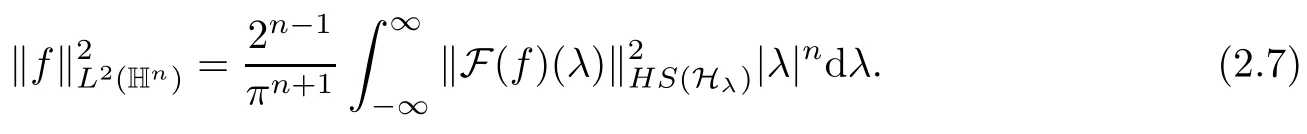
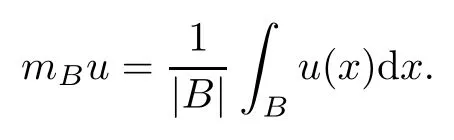
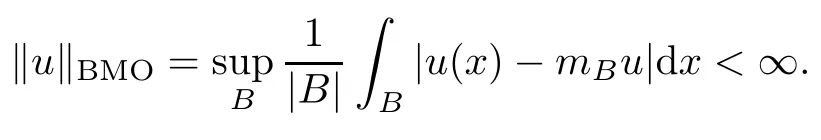
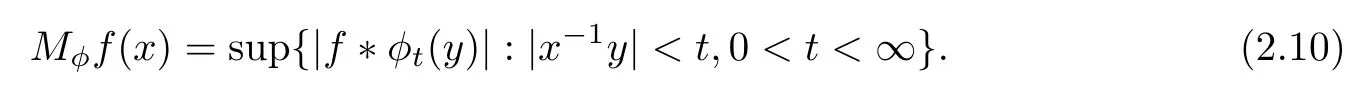
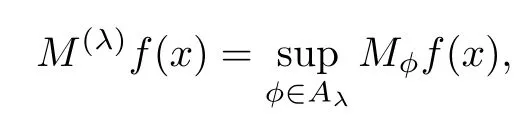
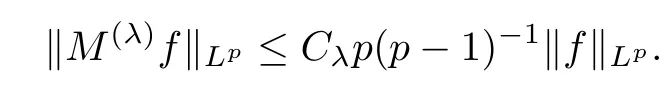
3 Boundedness of Bilinear Spectral Multipliers
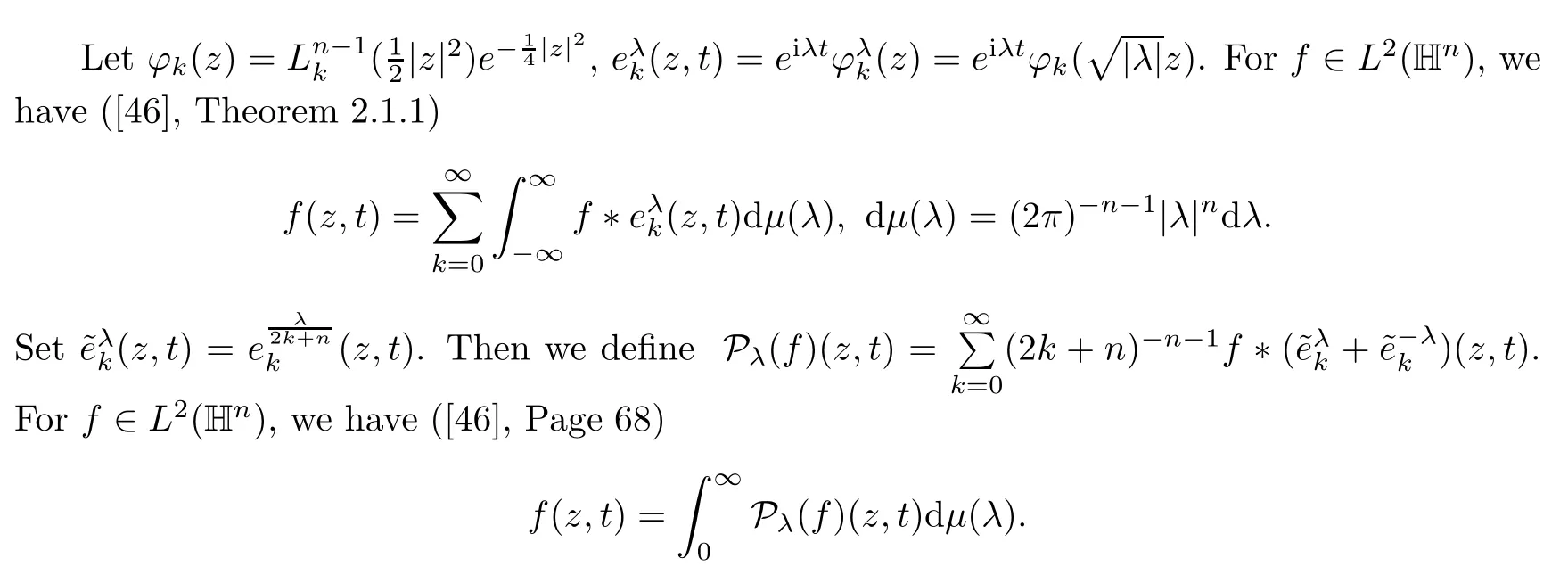
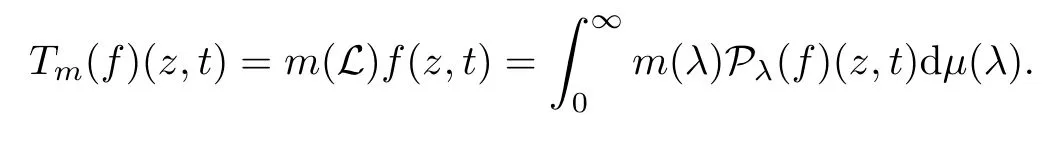
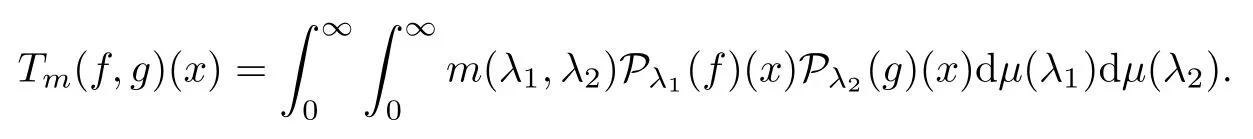
3.1 m(λ1,λ2)is supported between the axis coordinates and the straight line
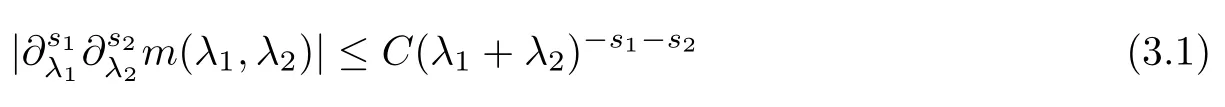
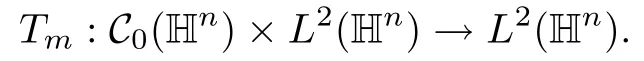
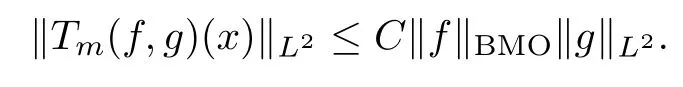


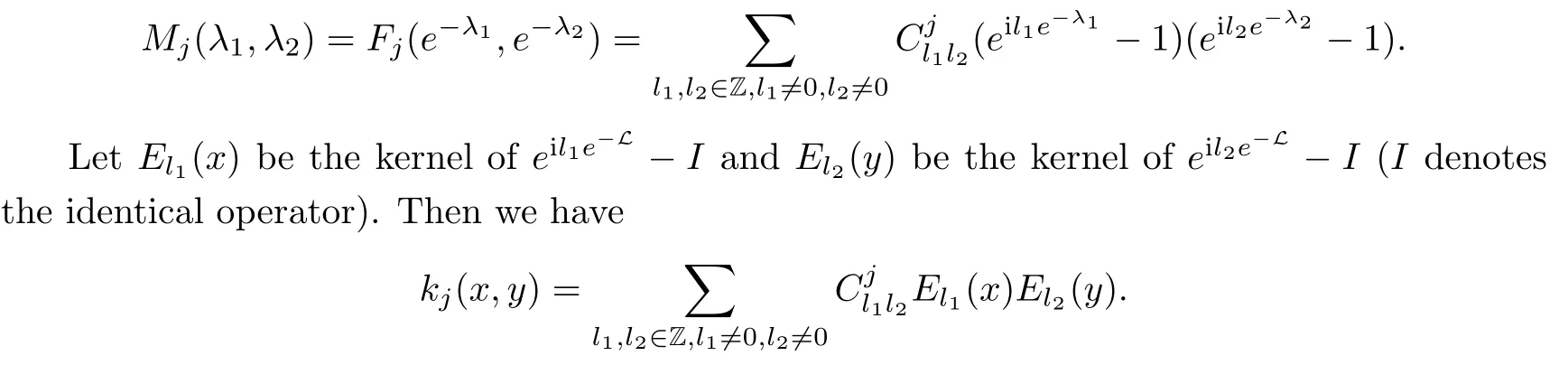
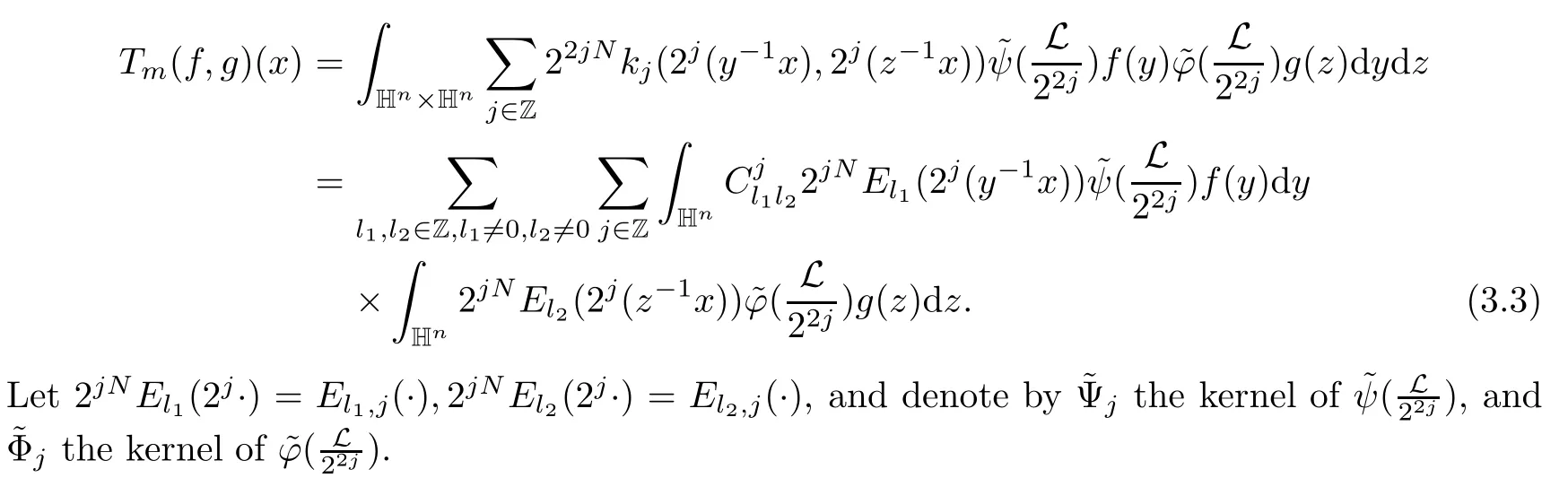

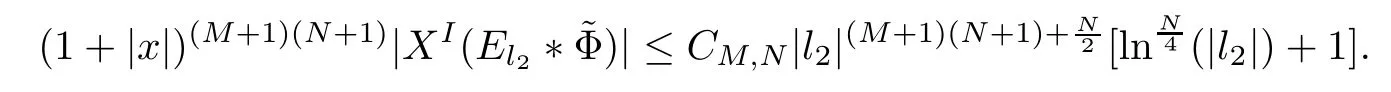

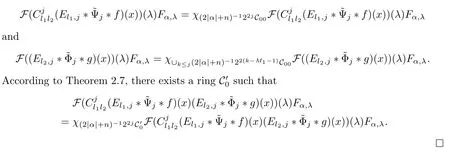
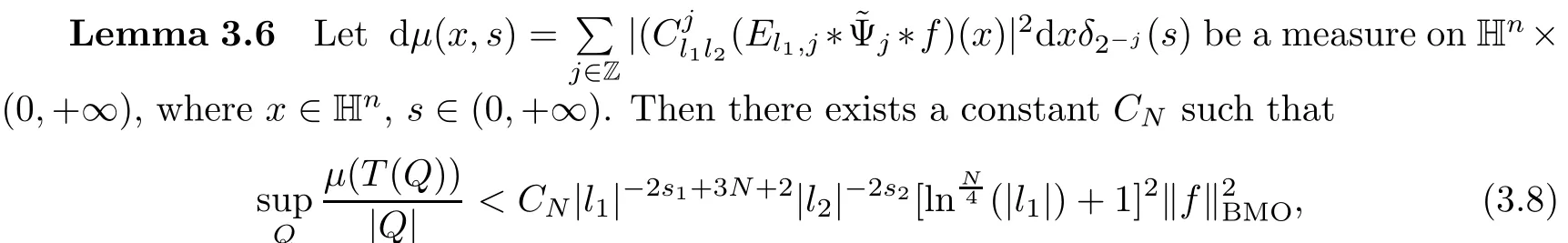
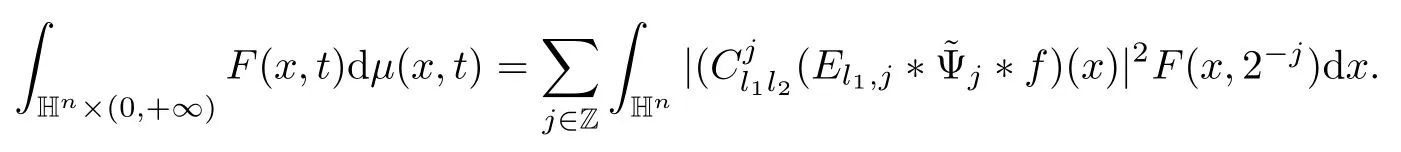
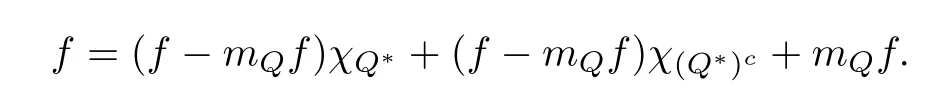
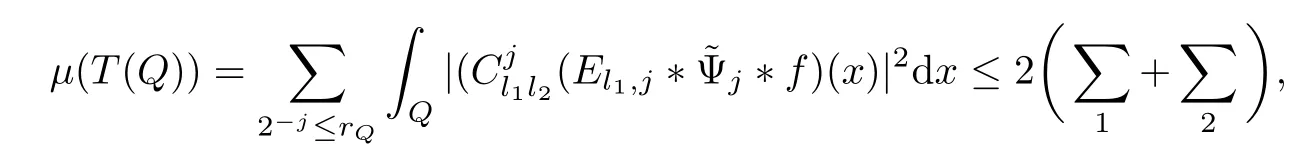
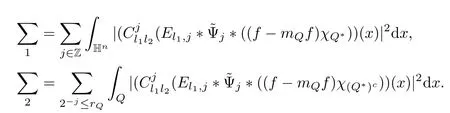
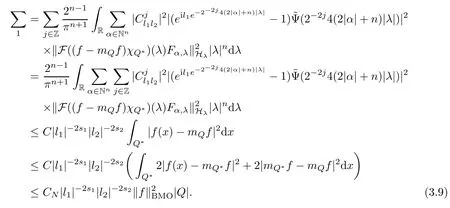

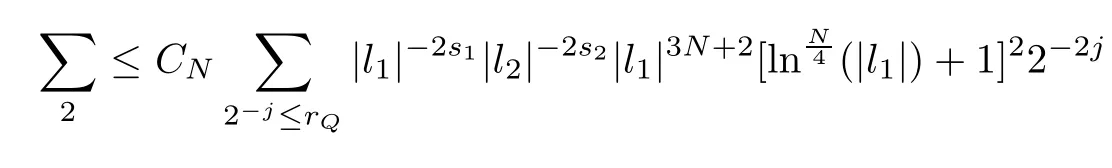
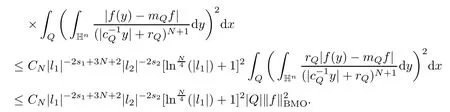
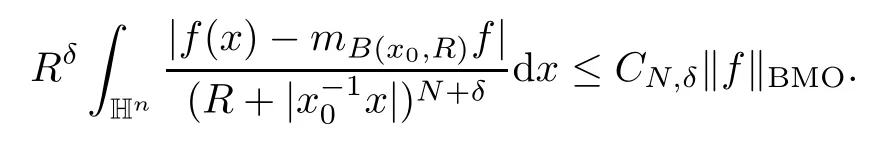

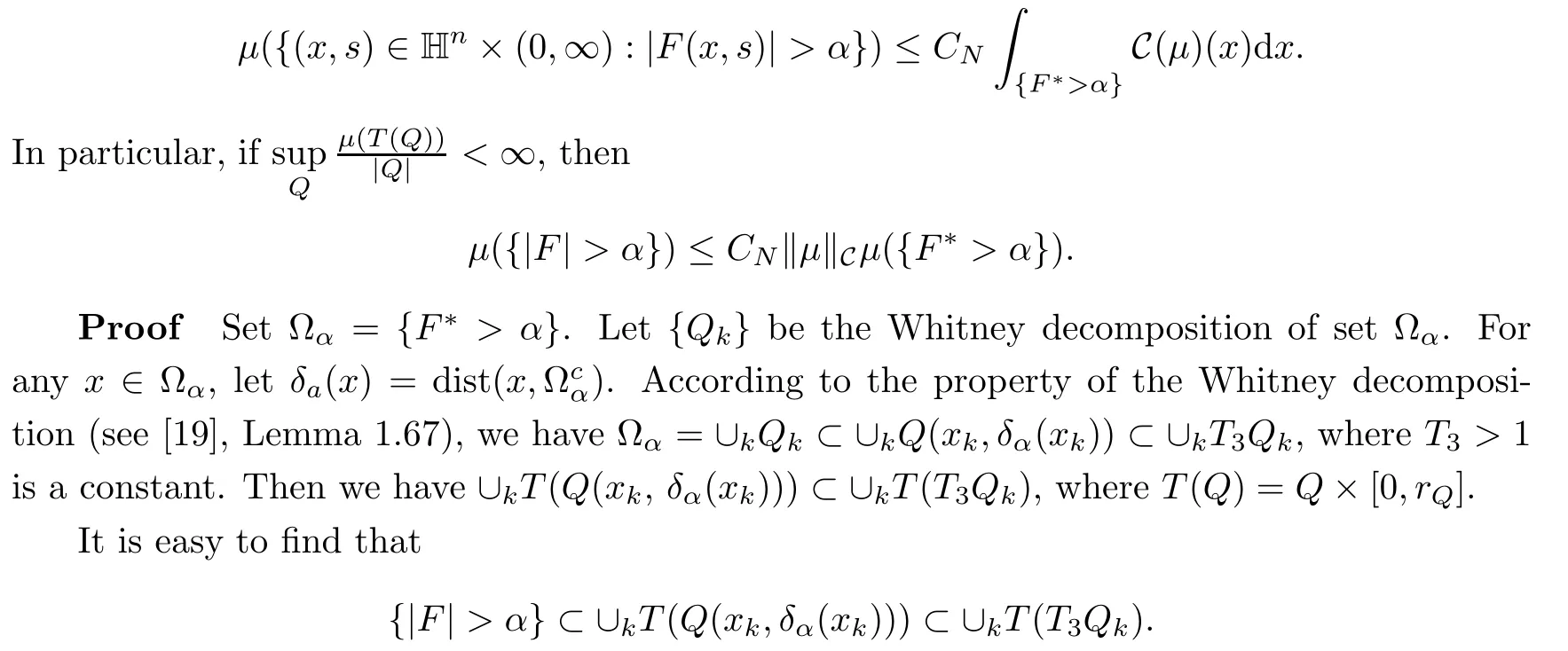
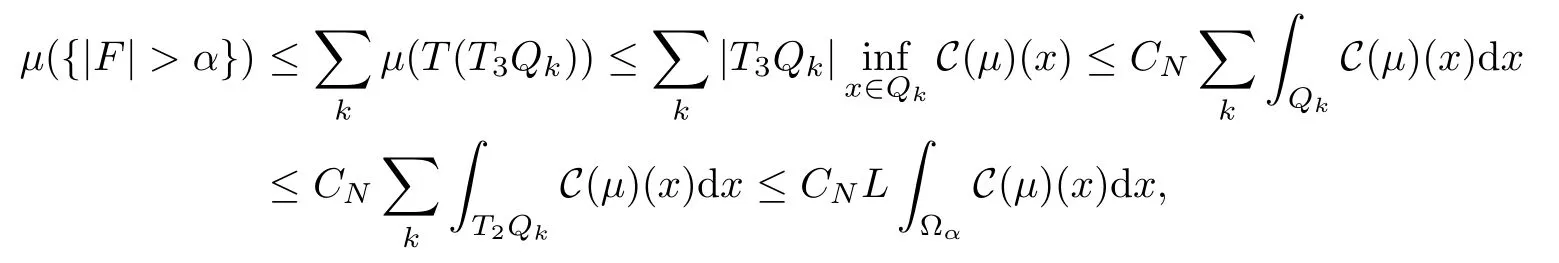
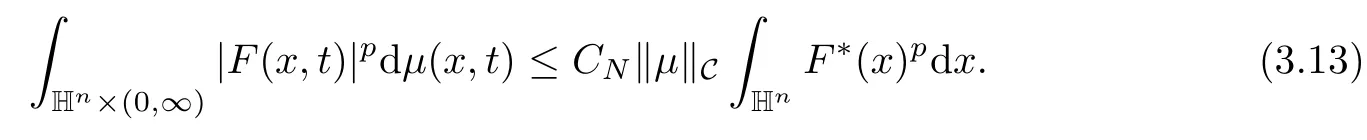
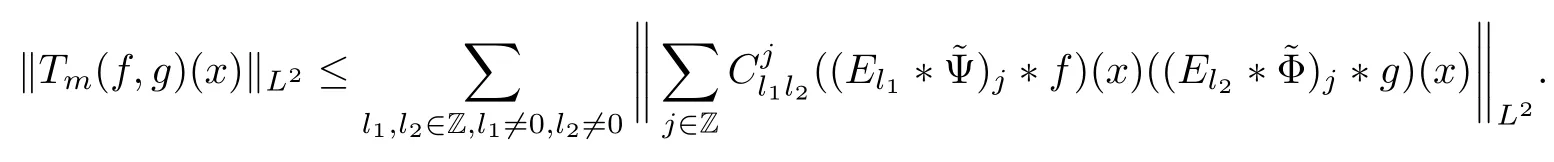
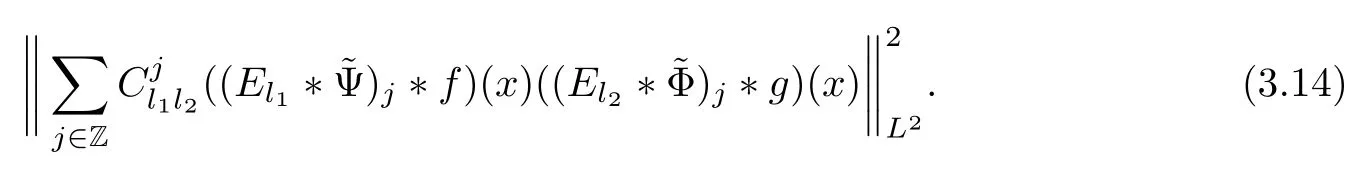
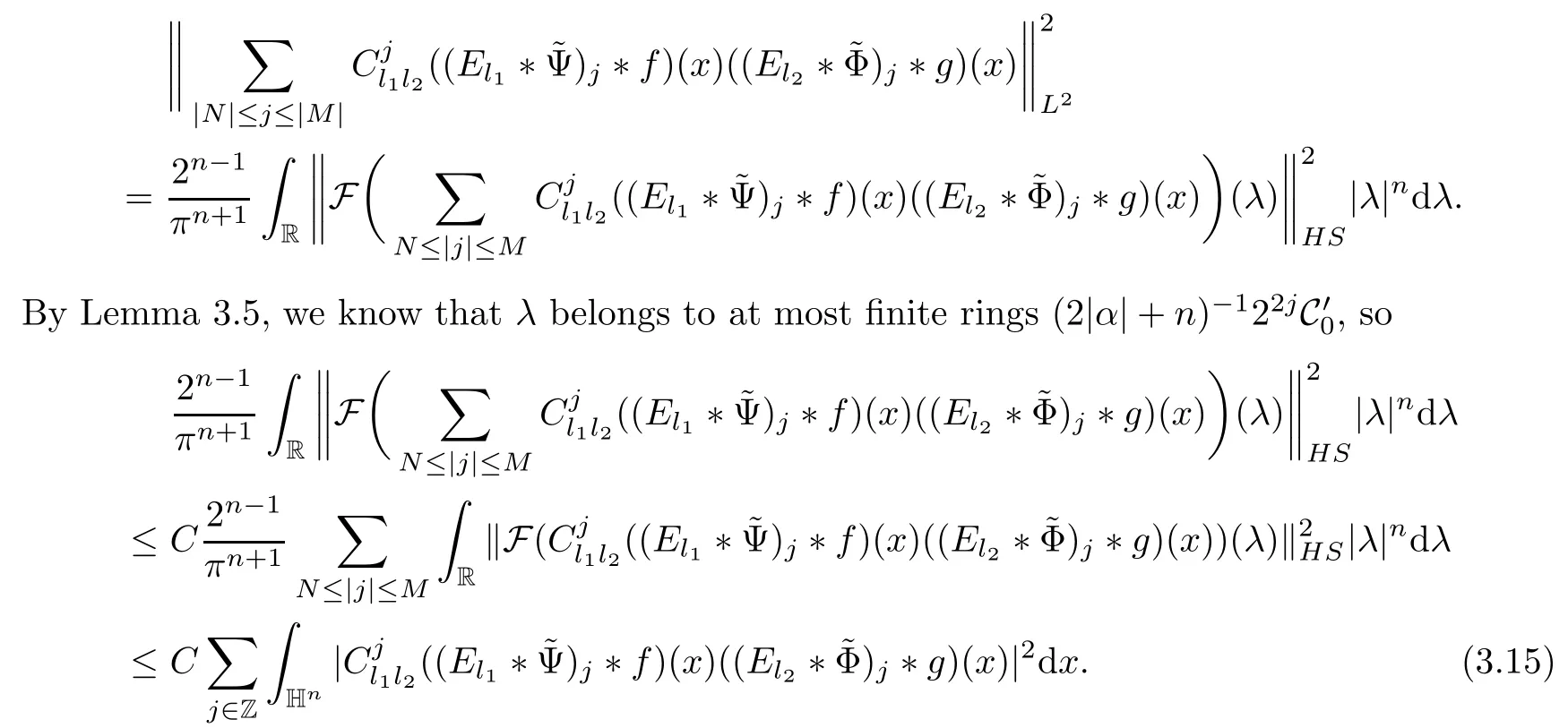
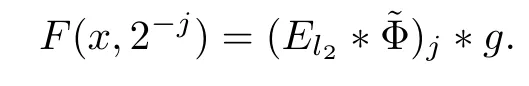
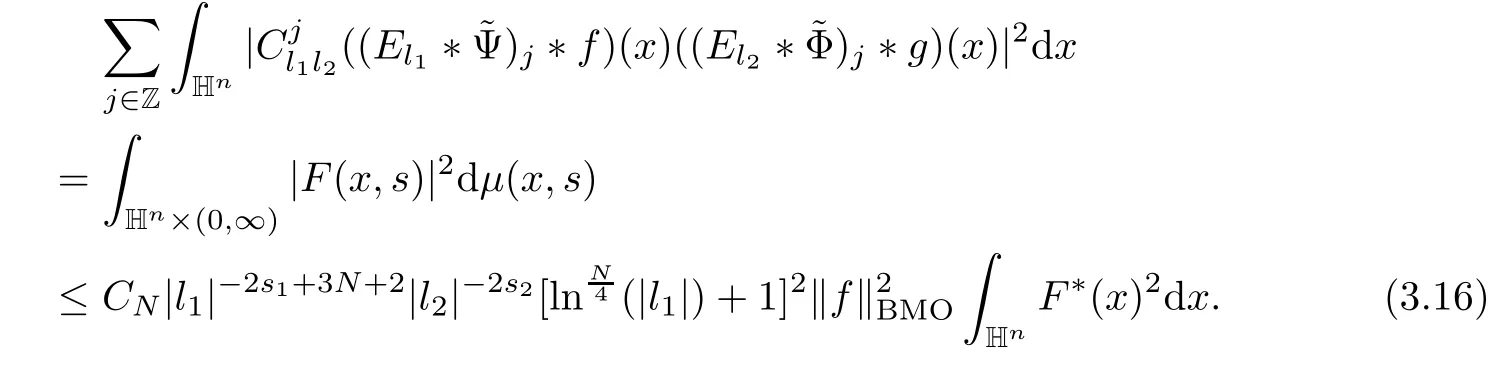
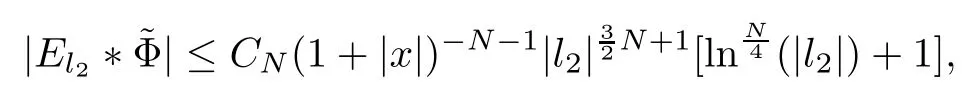
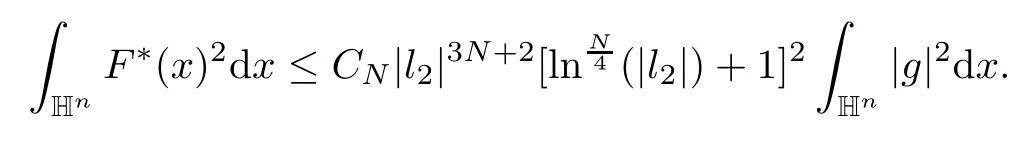
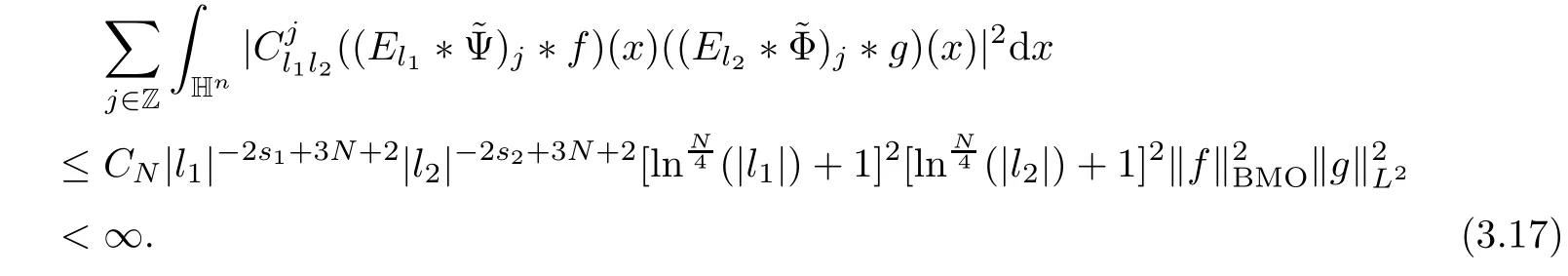
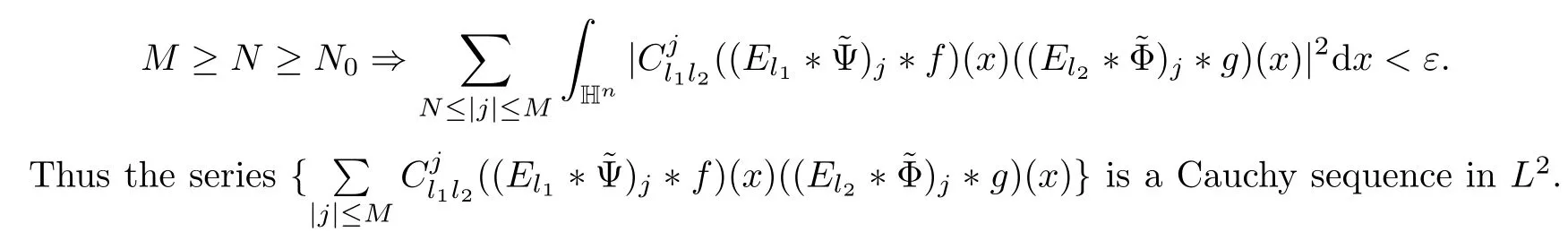
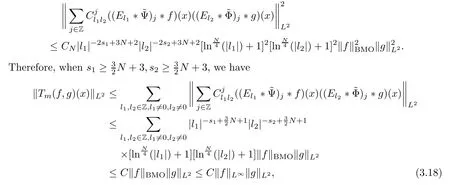
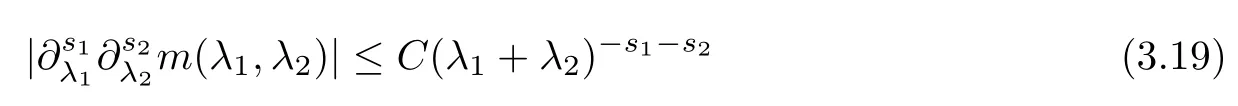
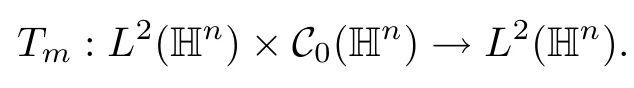
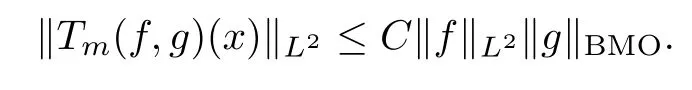
3.2 m(λ1,λ2)is supported between two straight lines
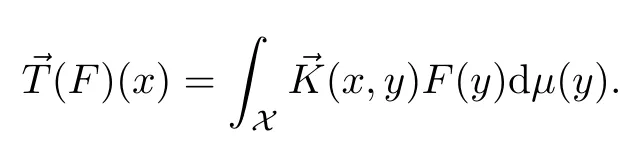
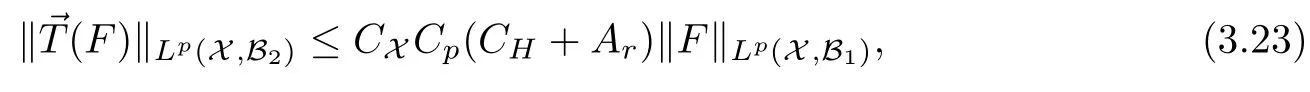
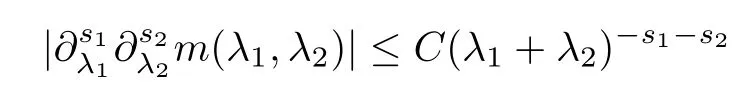
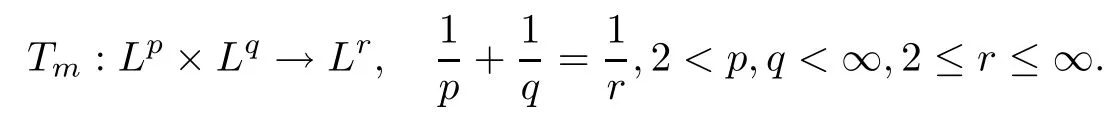


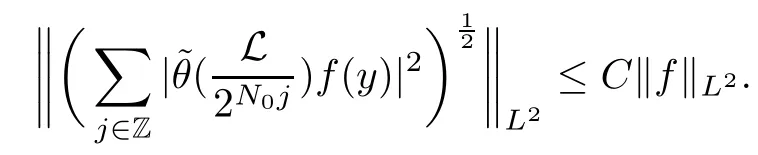

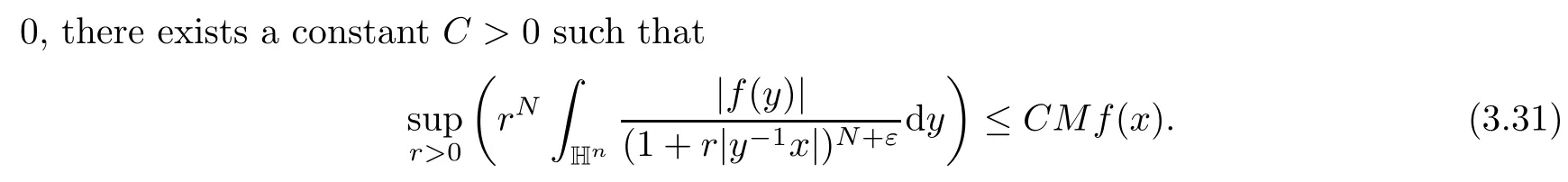
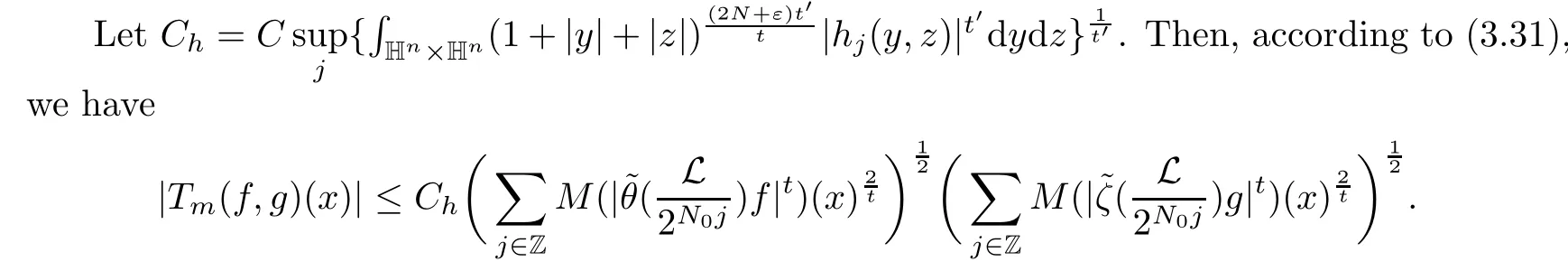

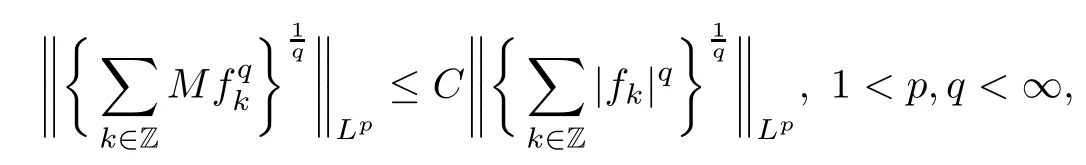
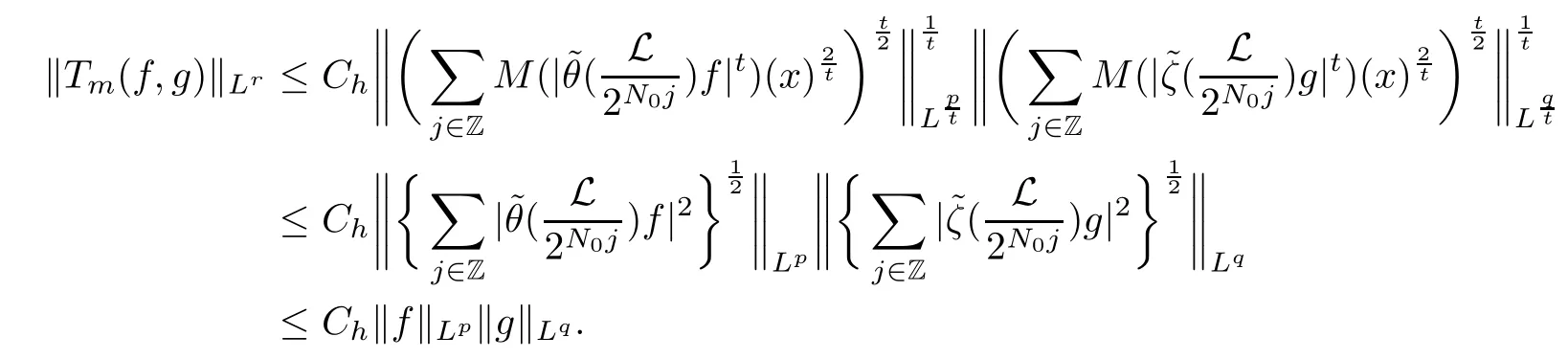

 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
