Higher-Order Rogue Wave Pairs in the Coupled Cubic-Quintic Nonlinear Schr?dinger Equations?
Tao Xu(徐濤),Wai-Hong Chan(陳偉康),and Yong Chen(陳勇),4,?
1Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China
2MOE International Joint Lab of Trustworthy Software,East China Normal University,Shanghai 200062,China
3Department of Mathematics and Information Technology,The Education University of Hong Kong,Hong Kong,China
4Department of Physics,Zhejiang Normal University,Jinhua 321004,China
AbstractWe study some novel patterns of rogue wave in the coupled cubic-quintic nonlinear Schr?dinger equations.Utilizing the generalized Darboux transformation,the higher-order rogue wave pairs of the coupled system are generated.Especially,the first-and second-order rogue wave pairs are discussed in detail.It demonstrates that two classical fundamental rogue waves can be emerged from the first-order case and four or six classical fundamental rogue waves from the second-order case.In the second-order rogue wave solution,the distribution structures can be in triangle,quadrilateral and ring shapes by fixing appropriate values of the free parameters.In contrast to single-component systems,there are always more abundant rogue wave structures in multi-component ones.It is shown that the two higher-order nonlinear coefficients ρ1and ρ2make some skews of the rogue waves.
Key words:higher-order rogue wave pairs,coupled cubic-quintic nonlinear Schr?dinger equations,generalized Darboux transformation
1 Introduction
Rogue waves(RWs)are modeled as a unique phenomenon that seems to appear from nowhere and disappear without a trace,[1]and can appear in a variety of fields,such as atmosphere,[2]super fluidity,[3]Bose-Einstein condensates,[4]nonlinear optics[5]and finance[6]and so on.These kinds of waves are characterized as being localized in both space and time,and are always written as rational form solutions in mathematics.It is well known that the standard nonlinear Schr?dinger(NLS)equation is an ideal model that describes the RW phenomenon.Besides,various types of rogue wave solutions associated with the NLS equation have been widely reported by many authors.[7?9]
There have been many articles on rogue waves of other single-component systems besides the standard NLS equation,such as the derivative NLS equation,[10?11]the Hirota equation,[12]the Kundu-Eckhaus equation,[13?14]the(3+1)-dimensional Jimbo-Miwa equation[15]and so on.Based on the fact that a variety of complex systems usually involve more than one component,such as nonlinear optical fibers and Bose-Einstein condensates,etc.,recent studies were extended to multi-component systems.[16?18]Cross-phase modulation effects are usually included in the coupled system,and the cross-phase modulation term can vary the instability regime.[19]For single-component systems,the RW solutions can be always correlated by Galileo transformation.Thus,the velocity of the background has no real effect of RWs’structures.For multicomponent coupled models,the relative velocity between different components cannot be annihilated by some special Galileo transformations,and this kind of velocity plays an important role in controlling various structures of RW solutions.[19?21]
Compared to single-component systems,a variety of novel and interesting results appeared in multi-component systems.[22?23]The four-petaled flower structure RWs were constructed in the three-component NLS equations through the Darboux transformation(DT).[20]The W-shaped soliton complexes and RWs were obtained in AB system.[21]Recently,various types interactional solutions were constructed in many different multi-component systems.[24?25]Bright-dark-rogue solutions were constructed in two-component NLS equations[26]and Hirota equations[27]by DT,respectively. Besides,the hybrid solutions that higher-order RWs interacting with multisoliton(or multi-breather)were constructed in various multi-component systems.[28?30]
In recent years,there have been several studies on RW pairs in multi-component coupled systems,[19,31?32]in which this kind of first-order RW pair solutions can include two first-order classical RWs.In this paper,we focus on constructing higher-order RW pairs of the following coupled cubic-quintic nonlinear Schr?dinger(CCQNLS)equations,which describe the effects of quintic nonlinearity on the ultrashort optical pulse propagation in non-Kerr media,[33?40]
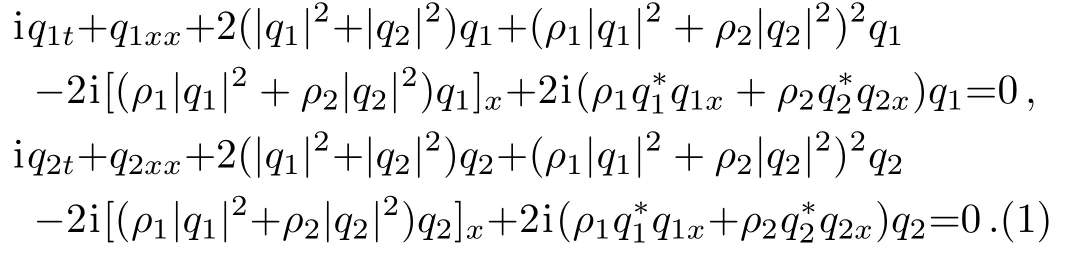
Here,q1and q2are the components of the electromagnetic fields along the coordinate x and t is the time.The parameters ρ1and ρ2are all real constants and the asterisk denotes complex conjugation.In the regime of ultrashort pulses,the standard NLS equation is less accurate.To meet this condition,the cubic and quintic nonlinear terms were added on the standard coupled NLS equations and formed the CCQNLS system(1).[34]Additionally,it is very necessary to construct some new RW pattern structures of the coupled system(1).
When q1=u,q2=0,and ρ1=2β,the CCQNLS system(1)can be reduced to the Kundu-Eckhaus equation.[13?14,41]In Refs.[35]and[42],the multi-soliton and bounded states of the CCQNLS equations(1)were obtained.Bright-bright,bright-dark and dark-dark solitons for the coupled system(1)were generated through Hirota bilinear method.[38?40]Besides,the multi-component generalization of the CCQNLS system(1)were investigated by DT.[43]Recently,the higher-order RWs of Eq.(1)were constructed through the generalized DT[37]and the authors considered the case that there is a double root in the characteristic equation.Motivated by the work in Refs.[19,32–33],we consider that the characteristic equation possesses a triple root,then some novel and interesting RW patterns of the CCQNLS system(1)can be generated through the generalize DT.Here,some dynamics of the RW pairs in the CCQNLS system(1)are exhibited.Besides,it is shown that some skews of RWs can be caused by two higher-order nonlinear coefficients ρ1and ρ2.
This article is organized as follows.In Sec.2,the generalized DT of the coupled cubic-quintic nonlinear Schr?dinger equations is constructed.In Sec.3,higherorder RW pairs are obtained and some dynamics structures are discussed in detail.The last section contains several conclusions and discussions.
2 Generalized Darboux Transformation for the CCQNLS System
The Lax pair of the CCQNLS system(1)can be expressed as[35,37,43]
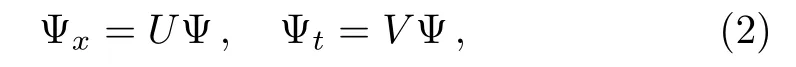
where Ψ =(ψ(x,t), ?(x,t), χ(x,t))T,T denotes the transpose of the vector,while U and V are all 3×3 matrices and they can be given as
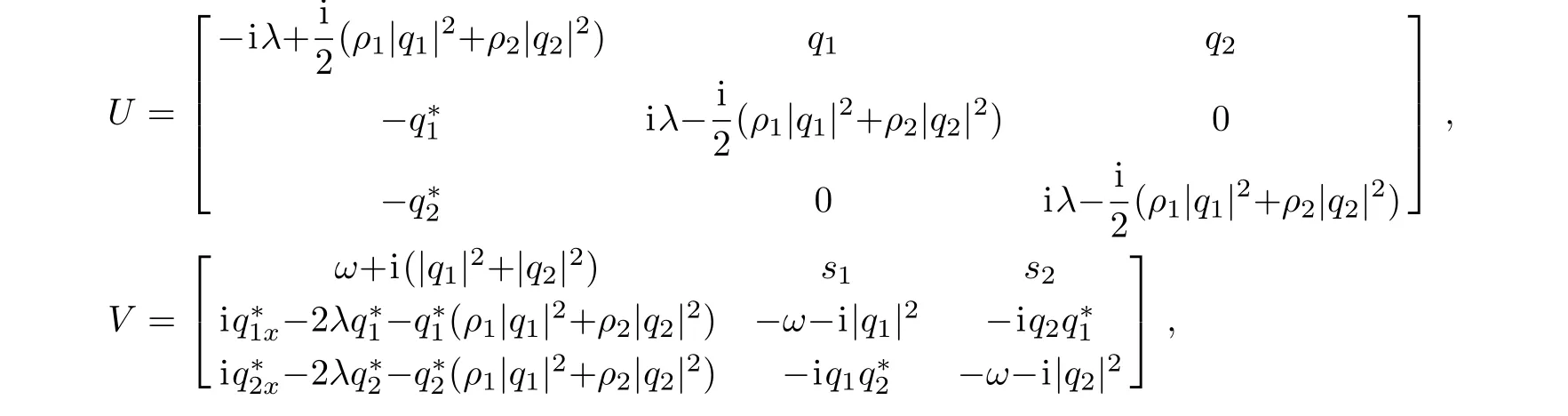
where
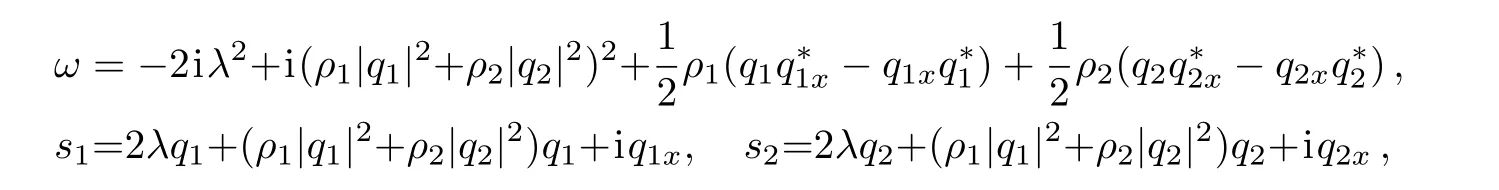
here,λ is the spectral parameter.Additionally,the CCQNLS system(1)can be directly derived from the compatibility condition Ut?Vx+[U,V]=0.
In what follows,based on the DT of the CCQNLS system(1)constructed in Refs.[35,37,43],the generalized DT of Eqs.(1)can be constructed.[9]Letbe a special vector solution of the Lax pair(2)with q1=q1[0],q2=q2[0],λ = λ1+δ and δ being a small parameter.It shows that Ψ1can be expanded as the Taylor series at δ=0
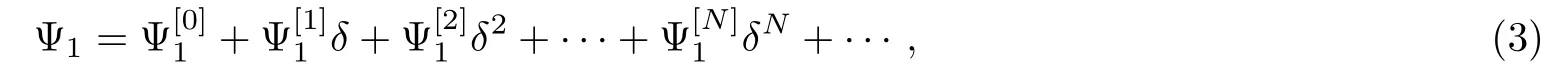
where
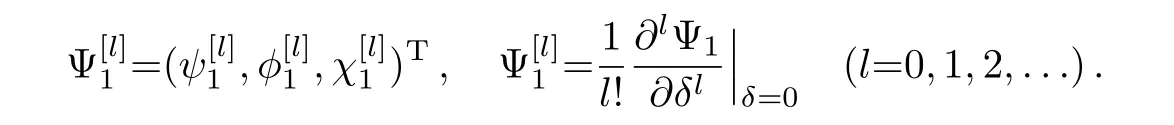
The N-step generalized DT of the CCQNLS system(1)can be written as follows
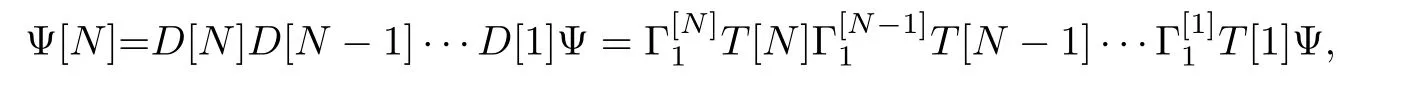
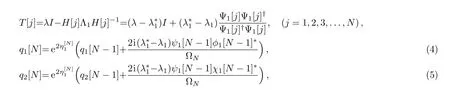
where I is 3×3 identity matrix and j=1,2,3,...,N.
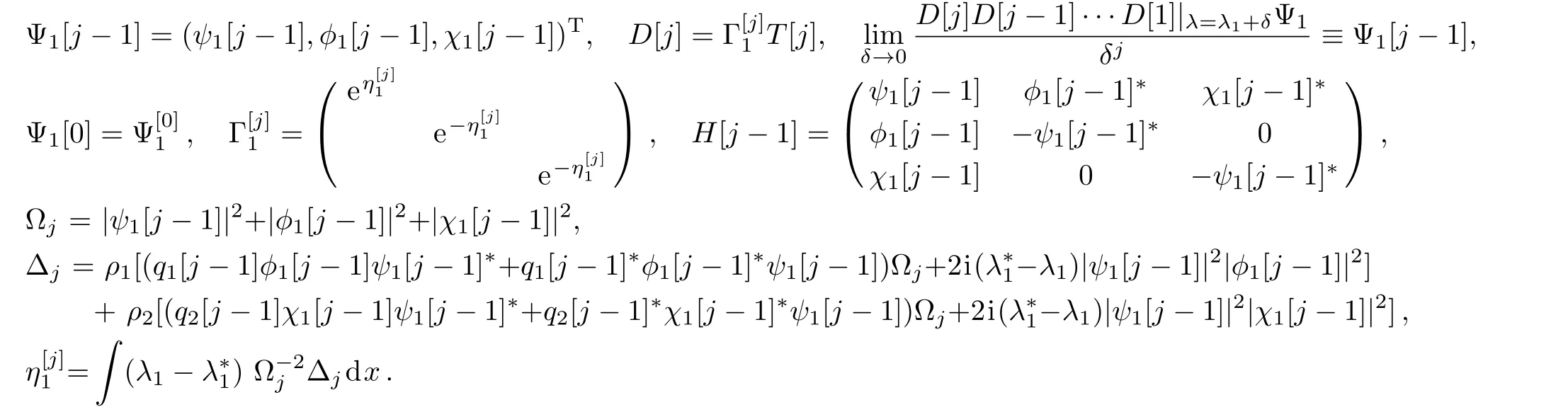
3 Higher-Order Rogue Wave Pairs
In the following,we choose a nontrivial seed solution of Eq.(1)
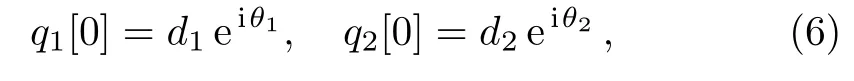
where
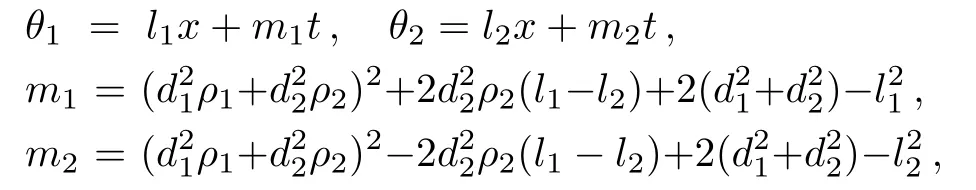
with di,mi,and li(i=1,2)being arbitrary constants.Besides,we need to convert the variable coefficient differential equations of Eq.(2)into constant coefficient ones by a gauge transformation.Setting ? =Mψ,the transformed Lax pair can be written as[26]
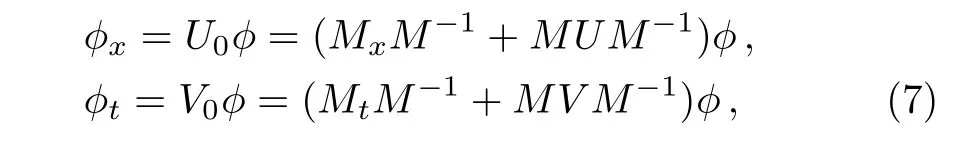
where
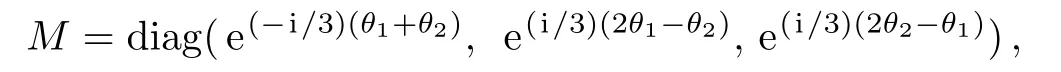
In Ref.[37],the authors constructed the RW solutions of Eq.(1)in the case that the characteristic equation of U0has a double root.Here,we hope to look for the higherorder RW pairs of Eq.(1)with the assumption that the characteristic equation of U0owns a triple root.In order to obtain the triple root,we choose the relevant free parameters in the seed solution Eq.(12)and the spectral parameter λ to admit the following conditions
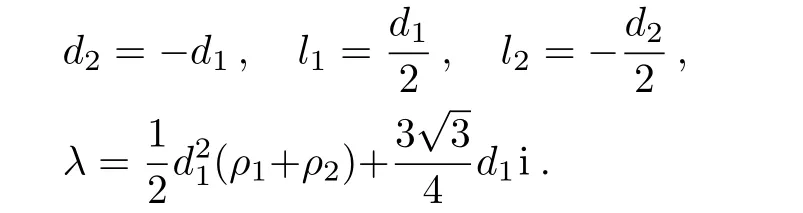
Without loss of generality,the parameter d1can be chosen as d1=1,then the above conditions can be rewritten as
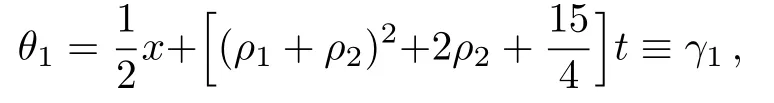
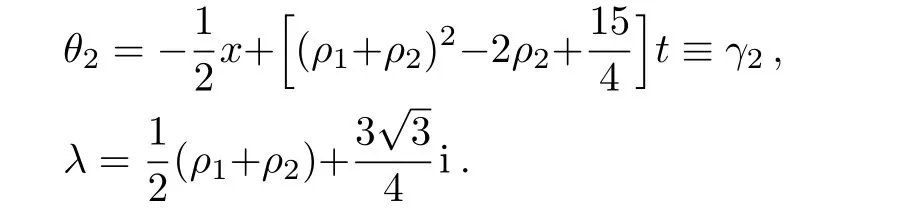
In order to utilize the limiting process,we set the spectral parameter
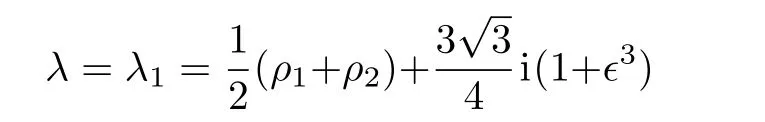
and ? be a small parameter,besides,the seed solution of Eq.(1)can be chosen as q1[0]=eiγ1,q2[0]= ? eiγ2.At this point,the fundamental solution of the Lax pair(2)can be expressed as
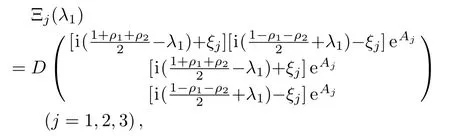
where
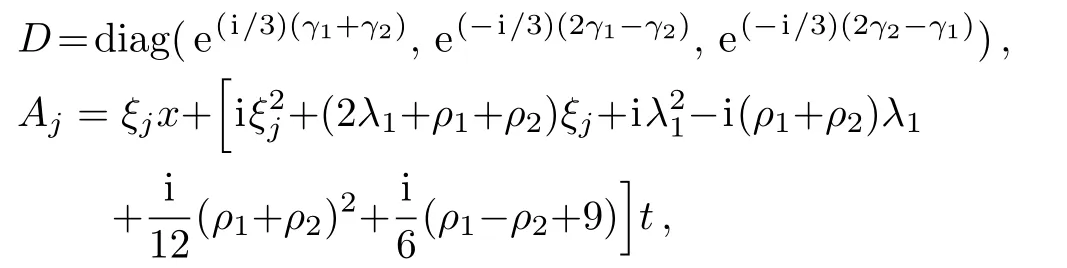
and ξjadmits the following cubic algebraic equation
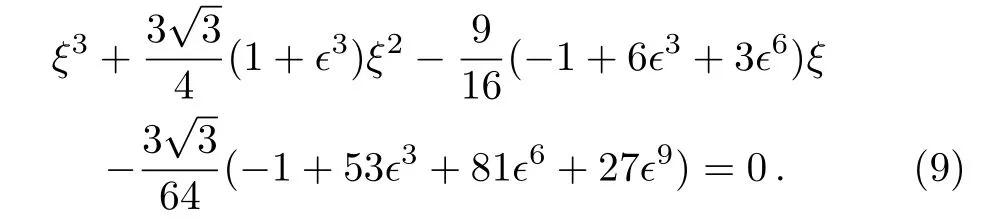
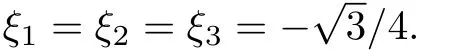
In order to construct the higher-order RW pairs of the CCQNLS Eq.(1)withandfor the above triple root case,the following special solution of the Lax pair(2)[19,33]can be given
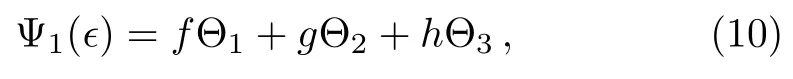
where
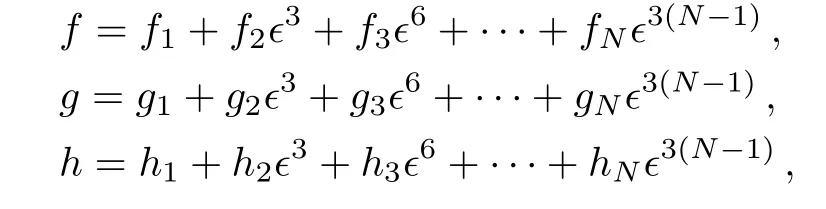
and
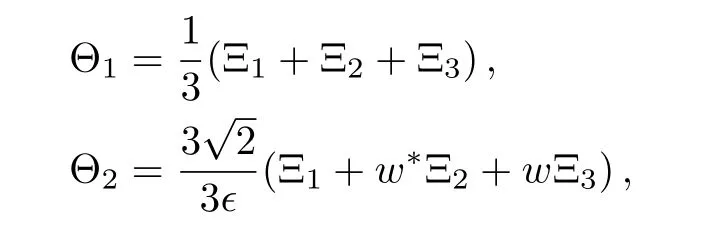
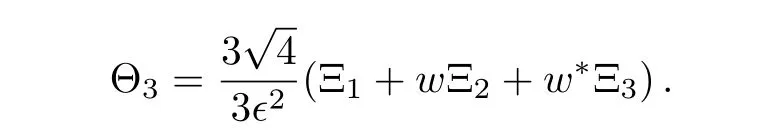
Here w=e2πi/3,and fj,gj,hj(j=1,2,3,...,N)are all real constants.Besides,the vector function Ψ1(?)in Eq.(11)can be expanded as the following Taylor series around ?=0
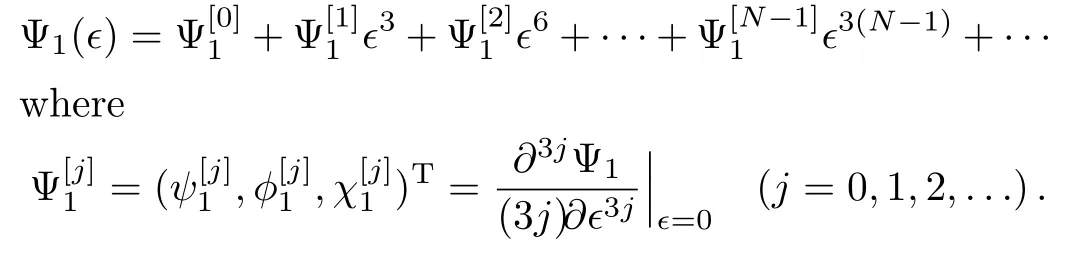
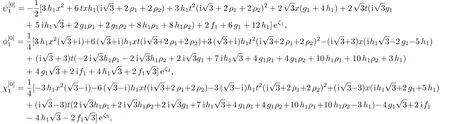
and
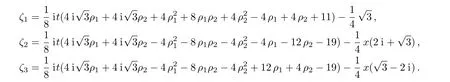
In order to avoid the complicated integral operation in the expressions ofwe give the following expressions of modules of qj[1]and qj[2](j=1,2)through the first-and second-step generalized DT
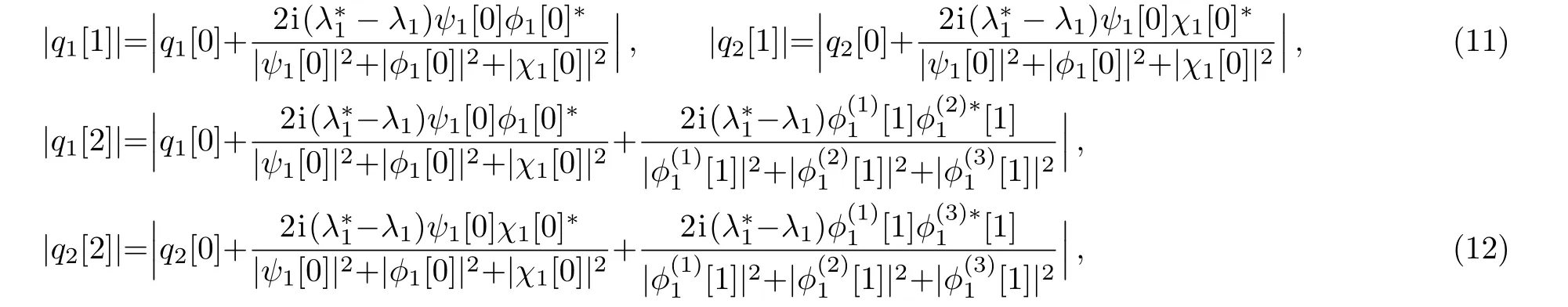
Through the formula(11),we can get the first-order RW pair of the CCQNLS system(1),see Figs.1–3.When f1=g1=h1=0,the first-order fundamental RW can appear in both components q1and q2.Besides,this kind of fundamental RW including more than one peak above the background plane is greatly different from the classical first-order fundamental one,see Fig.1.Whenthe first-order fundamental RW splits into two standard first-order fundamental RW,see Fig.2.Interestingly,a high RW comes before a low one in Fig.2(a);and a low RW comes before a high one in Fig.2(b).In conclusion,we find that the above kind of RW pair can not be derived in single-component systems.[9?10,12?14]For two-component systems,[37,43]we can also conclude that the RW pair cannot be obtained when there is a double root in the characteristic equation of the transformed matrix in the x-part of the Lax pair.
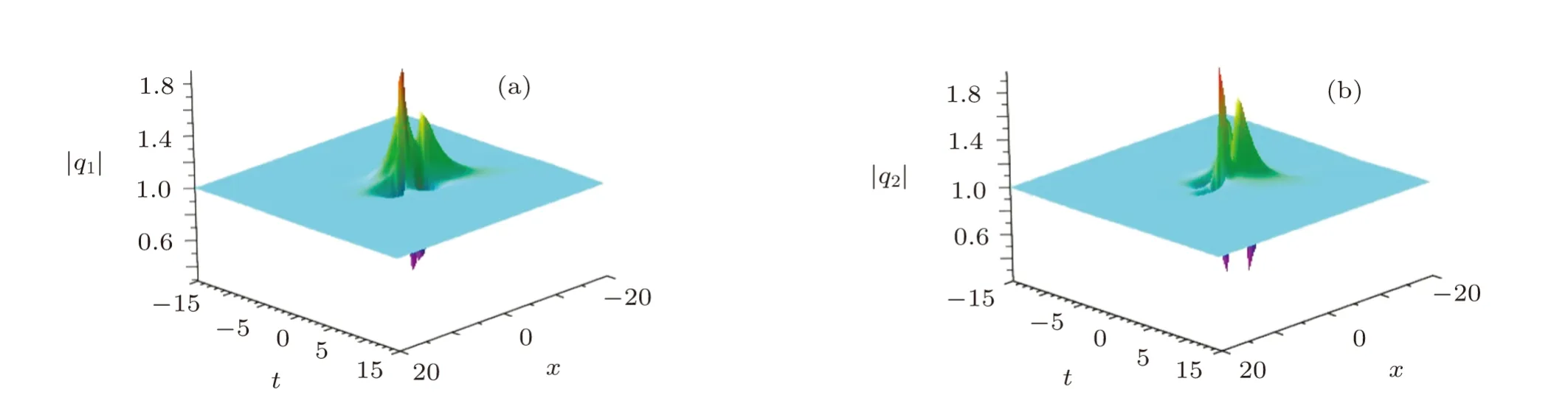
Fig.1 Evolution plot of the first-order fundamental RW in the CCQNLS equations by choosing ρ1=1/3,ρ2=1/4,f1=g1=0,h1=1:(a)q1;(b)q2.

Fig.2 Evolution plot of the first-order RW pair in the CCQNLS equations by choosing ρ1=1/3,ρ2=1/4,f1=100,g1=0,h1=1:(a)q1;(b)q2.
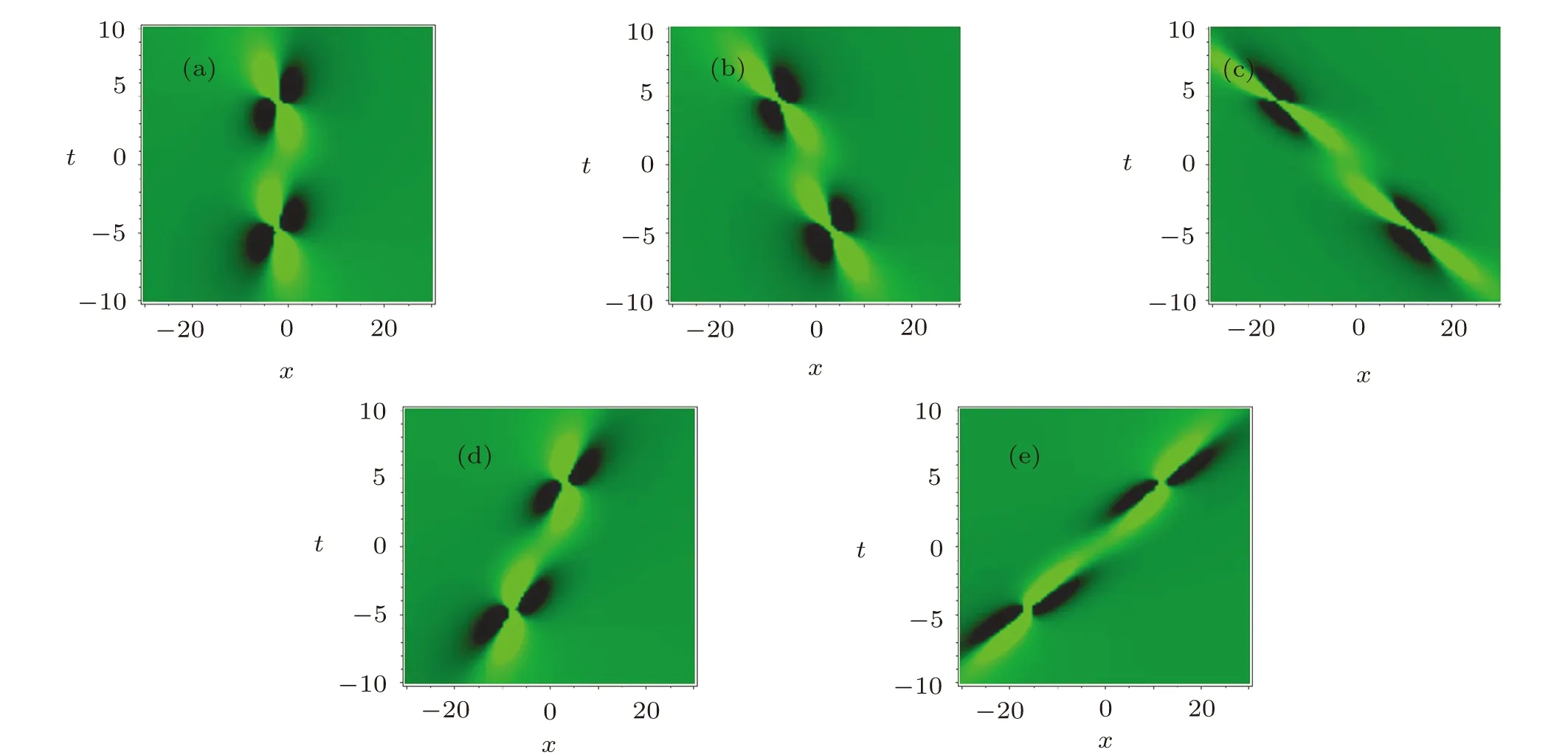
Fig.3 Evolution density plot of the first-order RW pair of the q1component in the CCQNLS equations by choosing f1=100,g1=h1=0:(a) ρ1= ρ2=0;(b) ρ1=1/3,ρ2=1/4;(c)ρ1=1/2,ρ2=1;(d) ρ1= ?1/3,ρ2= ?1/4;(e)ρ1= ?1/2,ρ2= ?1.
In order to investigate the effects of higher-order nonlinear terms in constructing the dynamics of RW in the CCQNLS equations,the density plots of q1component are given in Fig.3 after choosing different values of higherorder nonlinear coefficients ρ1and ρ2.From Figs.3(a)–3(e),it can be found that the higher-order nonlinear terms make an important skew angle relative to the ridge of the RW in counter-clockwise if ρ1>0,ρ2>0 and in clockwise if ρ1<0,ρ2<0 by increasing the absolute values of ρ1and ρ2.[13]The same dynamic structure can be also demonstrated in q2component and we omit these figures here.
In a similar way,the second-order RW pairs of the CCQNLS equations(12)can be derived through the related formula(1).Compared to the first-order case,the distributions of second-order one have more different patterns.There are six free parameters in the expressions of the second-order RW solution including fj,gj,and hj(j=1,2),which can be assigned to different values to obtain various patterns.Similarly to the first-order case,the higher-order nonlinear coefficients ρ1and ρ2can also make an important skew angle relative to the ridge of the RWs.Through either choosingor g1=0,[19]we can respectively construct two types of second-order RW pairs including four or six fundamental RWs.

Fig.4 Evolution plot of the second-order RW pairs of triangular pattern in the CCQNLS equations by choosing f1=0,g1=1,h1=0,f2=g2=0,h2=100,ρ1=1/3,ρ2=1/4:(a)q1;(b)q2.

Fig.5 Evolution plot of the second-order RW pairs of line pattern in the CCQNLS equations by choosing f1=0,g1=1,h1=0,f2=g2=0,h2=100,ρ1=1/2,ρ2=1:(a)q1;(b)q2.

Fig.6 Evolution plot of the second-order RW pais of quadrilateral pattern 1 in the CCQNLS equations by choosing f1=0,g1=1,h1=0,f2=10000,g2=0,h2=0,ρ1=1/3,ρ2=1/4:(a)q1;(b)q2.

Fig.7 Evolution plot of the second-order RW pais of quadrilateral pattern 2 in the CCQNLS equations by choosing f1=0,g1=1,h1=0,f2=10000,g2=0,h2=0,ρ1=1/2,ρ2=1:(a)q1;(b)q2.

Fig.8 Evolution plot of the second-order RW pairs of ring pattern 1 in the CCQNLS equations by choosing f1=g1=0,h1=1/100,f2=0,g2=1000,h2=0,ρ1=1/3,ρ2=1/4:(a)q1;(b)q2.
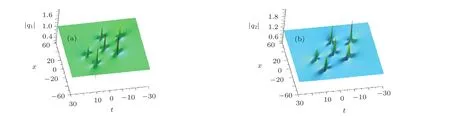
Fig.9 Evolution plot of the second-order RW pairs of ring pattern 1 in the CCQNLS equations by choosing f1=g1=0,h1=1/100,f2=10000,g2=h2=0,ρ1=1/3,ρ2=1/4:(a)q1;(b)q2.
When g1=0,the second-order RW pairs including six fundamental RWs are shown in Figs.8 and 9.These kinds of second-order RW structures are novel and interesting,which are not possible to emerge from the second-order ones in the single-component systems.In Fig.8,four classical first-order fundamental RWs distribute around one classical second-order fundamental RW,which constructs the ring pattern 1.It shows that five standard first-order RWs distribute around one classical first-order fundamental RW in Fig.9.Here,the higher-order nonlinear terms also make some skew angle relative to the ridge of the RWs.Changing the values of higher-order nonlinear coefficients ρ1and ρ2,the different patterns corresponding to ring pattern 1 and pattern 2 will be exhibited,respectively.As some detailed discussion has been made before,we omit these figures after changing ρ1and ρ2.Ulteriorly,a lot of other higher-order RW pairs can be constructed through iterating the generalized DT of the CCQNLS equations.
4 Conclusion
In this paper,we devote to investigate some novel patterns of RWs in the CCQNLS system(1).Based on the condition that the characteristic equation of the constant coefficient transformed matrix of U in the Lax pair(2)owing a double root,the authors[37]constructed the classical higher-order RWs of the CCQNLS system(1).Through considering that the characteristic equation of the transformed matrix U0of x-part of the Lax pair(2)owning a triple root,the higher-order RW pairs of the CCQNLS equations are constructed by the generalized DT.Besides,these kinds of RW pairs are greatly different from classical RWs in the CCQNLS system(1),for example,the first-order RW pair can include two classical first-order RWs,see Fig.2.These kinds of RW pairs were also constructed in some other systems,such as the coupled NLS equations,[19]the Sasa-Satsuma equation[31]and the three-wave resonant interaction equations.[32]
In Ref.[31],the RW pairs can be obtained in singlecomponent Sasa-Satsuma equation,because the Lax pair of the Sasa-Satsuma equation owns 3×3 matrices and the characteristic equation of the corresponding matrice can own a triple root under some special conditions.We can draw a conclusion that these kinds of RW pairs may be obtained through the generalized DT in the nonlinear systems whose Lax pair including the matrices larger than 2×2.
Especially,the first-and second-order RW pairs are discussed in detail.It demonstrates that two classical fundamental RWs can be emerged from the first-order RW.Besides,four or six classical fundamental RWs can exist in the second-order case,respectively.For the secondorder RW pairs,the distribution shape can be triangle,quadrilateral and ring structures.Besides,the higherorder nonlinear terms in the CCQNLS system(1)can affect the dynamic of the RWs.Increasing the absolute values of ρ1and ρ2,an important skew angle relative to the ridge of the RW can be shown in Figs.3,5,and 7.If ρ1>0,ρ2>0,with these two parameters getting larger,a larger movement for the humps in the counter-clockwise direction on the x-t plane is produced by the higher-order nonlinear terms;on the other hand if ρ1>0,ρ2>0,a larger movement for the humps in clockwise on the x-t plane is shown with the absolute values of the two parameters being larger.Our results further reveal the dynamic structures of RWs in a coupled system,and we hope these kinds of higher-order RW pairs presented in this paper could be verified in physical experiments in the future.
Acknowledgment
We would like to express our sincere thanks to other members of our discussion group for their valuable comments.
 Communications in Theoretical Physics2018年8期
Communications in Theoretical Physics2018年8期
- Communications in Theoretical Physics的其它文章
- A Numerical Investigation of Nanocomposite of Copper and Titanium Dioxide in Water Based Fluid Influenced by Instigated Magnetic Region
- Effects of Thermal Radiation on a 3D Sisko Fluid over a Porous Medium Using Cattaneo-Christov Heat Flux Model?
- Energy Transfer in the Light-Harvesting Complexes of Purple Bacteria?
- Effect of Critical Beam Radius on Self-focusing of cosh-Gaussian Laser Beams in Collisionless Magnetized Plasma
- Phase Sensitive Photonic Flash?
- Jeans Instability of Self Gravitating Dust Cloud in Presence of Effective Electrostatic Pressure
