Lump Solutions and Interaction Phenomenon for(2+1)-Dimensional Sawada–Kotera Equation?

Li-Li Huang(黃麗麗)and Yong Chen(陳勇)

Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China

MOE International Joint Lab of Trustworthy Software,East China Normal University,Shanghai 200062,China

1 Introduction

The so-called(2+1)-dimensional Sawada–Kotera equation

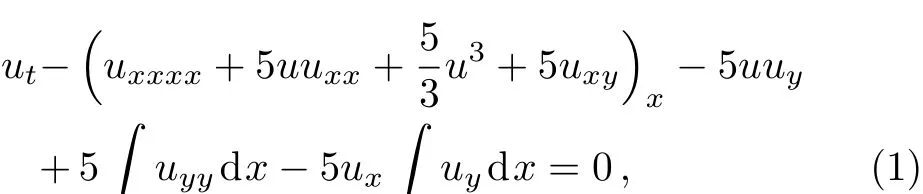
was first proposed by Konopelchenko and Dubrovsky,[1]whereuis a function of the variablesx,y,andt.This equation can be obtained by assembling of the first two KdV equations.Whenu(x,y,t)≡u(x,t),Eq.(1)becomes the Sawada–Kotera equation

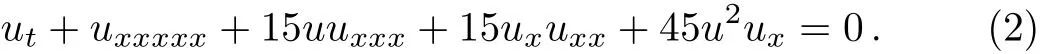
Equation(1)was widely used in many branches of physics,such as two-dimensional quantum gravity gauge field,conformal field theory and nonlinear science Liouvile flow conservation equations.In Ref.[2],the equation was decomposed into three(0+1)-dimensional Bargmann flows and obtained its explicit algebraic-geometric solution.In Ref.[3],four sets of bilinear B?cklund transformations were constructed to derive multisoliton solutions. In Ref.[4],the multi-wave method was used to seek for wtype wave solution,periodic soliton wave solutions,and three soliton wave solutions.In Ref.[5],the equation has been studied in the view point of Bell polynomials and its Lax pair can be found in Refs.[5–7].In Ref.[8],its Bilinear bell polynomials was obtained.In Refs.[9–12],the equation’s symmetry analysis was studied.In Ref.[13],Multiple soliton solutions and multiple singular soliton solutions were derived for the equation.In Ref.[14],double periodic wave solutions were obtained.

It is well known that all integrable equations possess soliton solutions,which reflect a common nonlinear phenomenon in nature.In the last decades,an increasing number of researchers have paid attention to the study of exact solutions,such as the rational solutions and the rogue wave,which exponentially localized solutions in certain directions.Compared with soliton solutions,lump solutions are a special kind of rational function solutions,localized in all directions in the space.The lump solution was first discovered[15]for its significant physical meanings.Many integrable equations have been found to possess lump solutions,such as the KPI equation,[16]the two-dimensional nonlinear Schr?dinger type equation,[16]the three-dimensional three wave resonant interaction equation,[17]the Ishimori equation.[18]

More recently,Ma[19]proposed a new direct method to obtain the lump solutions of the KP equation with Hirota bilinear method.This method is natural and interesting to search for lump solutions to nonlinear partial differential equations. Based on this method,the lump solutions of some more integrable equations have been found,such as dimensionally reduced p-gKP and p-gBKP equtions,[20]Boussinesq equation,[21]dimensionally reduced Hirota bilinear equation.[22]In addition,it isreported that lump solutions for some nonlinear partial differential equations restore their amplitudes,velocities,shapes after the interaction with solitons,which means the interaction among them can be considered completely elastic.[23?25]However,for some integrable equations,the interactions turned out to be completely non-elastic under a certain conditions.[26?28]In fact,in many nonlinear science fields such as the laser and optical physics,gas dynamics,hydrodynamics,plasma physics,nuclear physics,passive random walker dynamics,and electromagnetics,the similar phenomenon have been observed.Therefore,it is very important to discuss the inelastic interactions between the solitary waves in certain integrable or nonintegrable system under strong physical backgrounds,and it may provide a theoretical tool in understanding and supporting the relevant dynamical behavior.

In this paper,we study the lump solutions and a completely non-elastic interaction between a lump and a stripe of the(2+1)-dimensional Sawada–Kotera equation.The rest of the paper is organized as follows:In Sec.2,lump solutions of the(2+1)-dimensional Sawada–Kotera equation are studied and some suffcient and necessary conditions are presented on the parameters involved in the solutions,2-dimensional curves,3-dimensional plots and density plots with particular choices of the involved parameters are presented to show the dynamic characteristics of the obtained lump solutions.In Sec.3,a completely non-elastic interaction between a lump and a stripe of the(2+1)-dimensional Sawada–Kotera equation is obtained and the process of interaction is showed.The last section contains a conclusion.

2 Lump Solutions to the(2+1)-Dimensional Sawada–Kotera Equation

By introducing a potential variablevx=uwithv=v(x,y,t),Eq.(1)reduces to

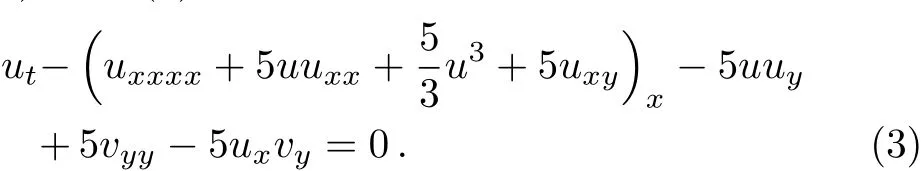
For Eq.(3),there exists a truncated Painlevé expansion[29]

withu0,u1,u2,?being the functions ofx,yandt,the function?(x,y,t)=0 is the equation of singularity manifold.Substituting(4)into(3)and balancing all the coefficients of different powers of?,we can get

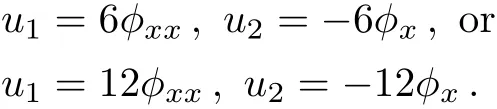
For the purpose of this paper,constructing the lump solutions of Eq.(1)from its bilinear form,we can take the vacuum solutionu0=0,which leads to

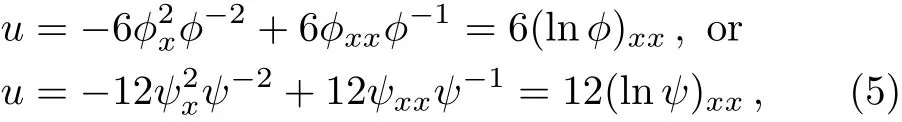
where?andψare two branches of the singular manifold.

Based on the truncated Painlevé expansion(5),corresponding to the branch of singular manifold,we substitute a dependent variable transformationu=6(lnf)xxwithf=f(x,y,t)into Eq.(1)yields an alternative bilinear representation for Eq.(1)as

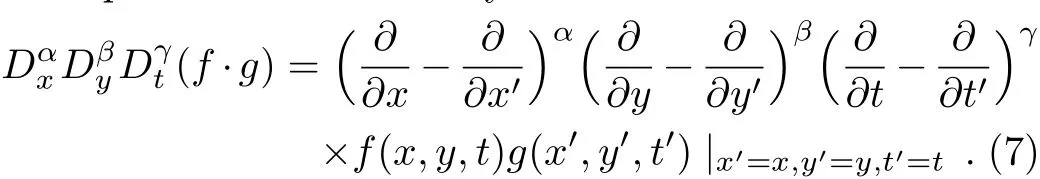
It is clear that iffsolves Eq.(6),thenu=u(x,y,t)is a solution to Eq. (1)through the transformationu=6(lnf)xx.

To search for lump solutions to the(2+1)-dimensional Sawada–Kotera equation in Eq.(6),we begin with quadratic function solutions with the assumption

with

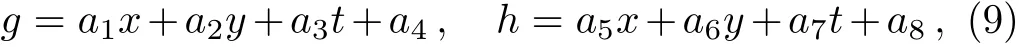
whereai(1≤i≤9)are all real parameters to be determined.In order to obtain the lump solutions,the positiveness offand localization ofuin all directions in the space need to be satisfied.Through a direct computation withfabove generates the following set of constraining equations for the parameters:

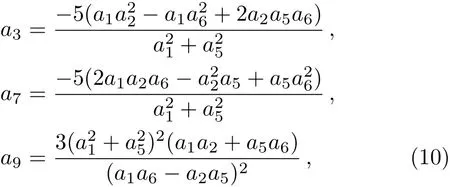
which need to satisfy the conditions

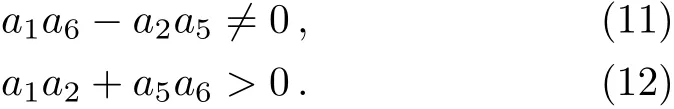
This leads to a class of positive quadratic function solutions to Eq.(6)

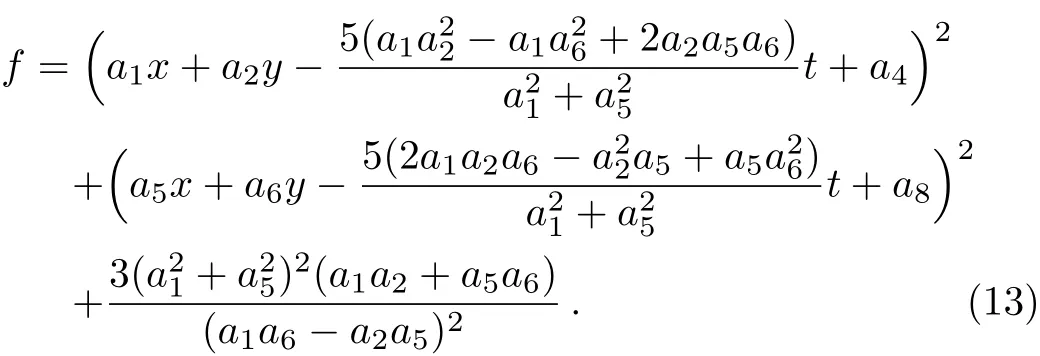
Then a class of lump solutions to the(2+1)-dimensional Sawada–Kotera equation(1)through the transformation

In this class of lump solutions, six parametersa1,a2,a4,a5,a6anda8are involved in the solutionu,whilea4anda8are arbitrary without conditions.

Two special pairs of positive quadratic function solutions and lump solutions with choosing specific parameters are given in the following.

First,a selection of the parameters:

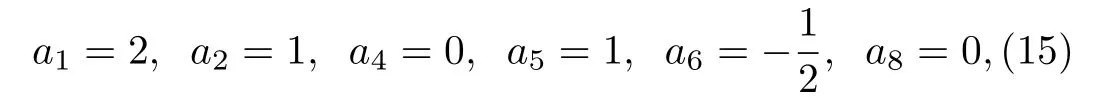
leads to

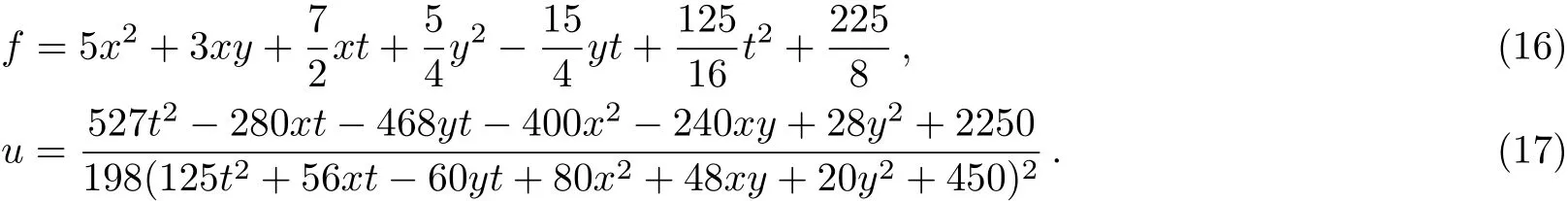
The plots whent=6 are depicted in Fig.1.

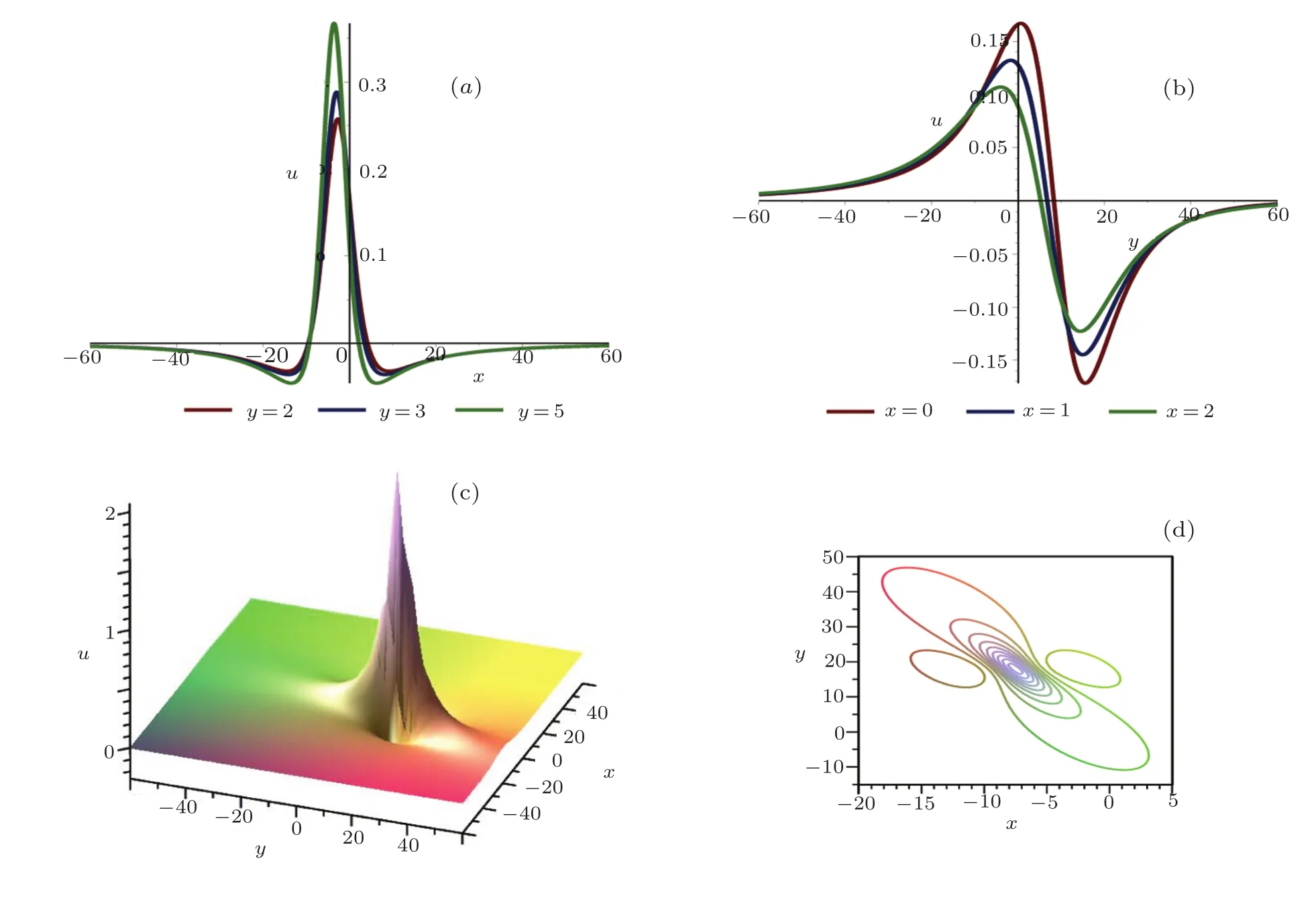
Fig.1 (Color online)Profiles of Eq.(17)with t=6:(a)x-curves;(b)y-curves;(c)the three-dimensional plot;(d)density plot.

Second,another selection of the parameters:

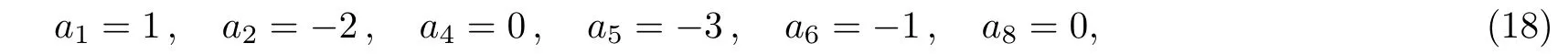
leads to

The plots whent=2 are depicted in Fig.2.

It is obviously observed that at any given timet,all the above lump solutions satisfy:

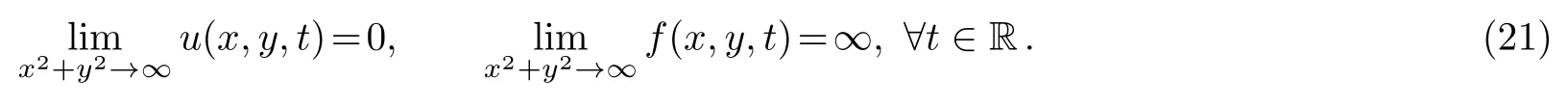
The lump solutions derived in this paper satisfy this criterion,and they are rationally localized in all directions in the space.

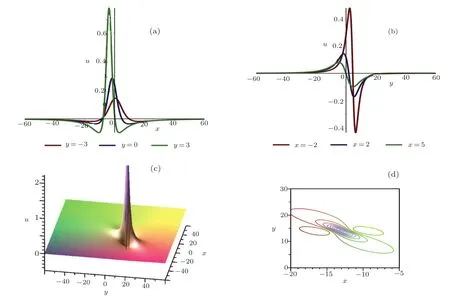
Fig.2 (Color online)Profiles of Eq.(20)with t=2:(a)x-curves;(b)y-curves;(c)the three-dimensional plot;(d)density plot.

3 Interaction Between a Lump and a Stripe of SK Equation

The interaction between a lump and a stripe of the(2+1)-dimensional Sawada–Kotera equation will be studied in this section.For the purpose of obtaining the interaction between rational solution and solitary wave solution,we rewrite the above functionf(x,y,t)into the following new form

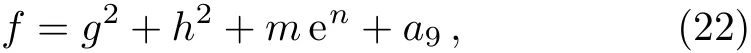
with

It is obvious that the functionf(x,y,t)consists of a rational function and an exponential function.Substituting Eq.(22)into Eq.(6),it can generate the following set of constraining equations for the parameters:

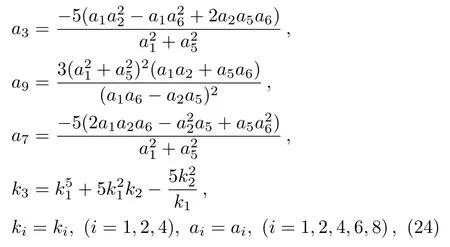
wherea1a6?a2a5/=0.Then the exact interaction solution ofuis expressed as follows:

In order to get the collision phenomenon,is essential.So the asymptotic behavior ofucan be obtained,whent→∞the solutionu→0.The asymbolic behavior shows that the lump is drowned or swallowed up by the stripe with the change of time.From the expression ofu,it is a mixed exponential-algebraic solitary wave solution.It presents a completely non-elastic interaction between two different solitons and decays both algebraically and exponentially.To illustrate the interaction phenomena between a lump and a stripe,we select the following parameters

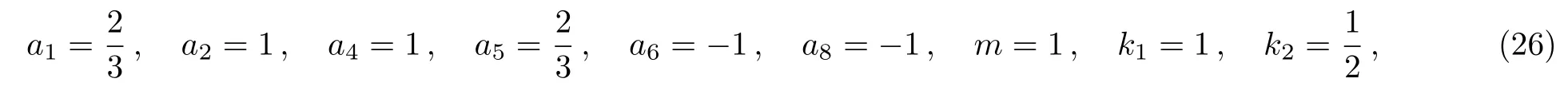
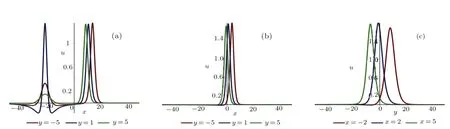
Fig.3 (Color online)Profiles of Eq.(25)with the parameters Eq.(26)(a)x-curves at t=?2;(b)x-curves at t=2;(c)y-curves at t=2.

Fig.4 (Color online)Profiles of interaction between a lump and a stripe with the parameters Eq.(26)at times(a)t=?6;(b)t=?0.5;(c)t=0;(d)t=0.5;(e)t=2;(f)t=6.

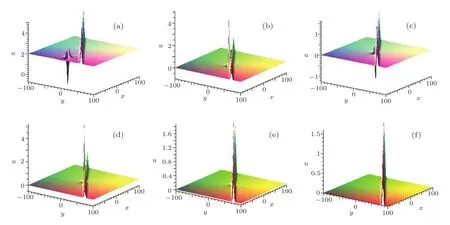
Fig.5 (Color online)Profiles of interaction between a lump and a stripe with k1=1,k2=3/2 in Eq.(26)at times(a)t=?6;(b)t=?0.5;(c)t=0;(d)t=0.5;(e)t=2;(f)t=6.

In order to investigate the interaction phenomenon betweenk3＞0 andk3＜0,we can changek1andk2in Eq.(25).whenk1=1,k2=1/2 in Eq.(26),the obtainedk3=9/4,and whenk1=1,k2=3/2,the obtainedk3=?11/4.Whenk3＞0,the asympototic behaviors in Fig.4 show the interaction phenomenon is consistent withk3＜0 in Fig.5.From the two pictures,we can see the interaction phenomena both happen neart=0,lump solutions are drowned or swallowed by stripe waves aftert=2.For a long time,the interaction phenomena are consistent betweenk3＞0 andk3＜0.

It is clear that whent→ ?∞,the solutionurepresents two solitary waves:the lump solution and the stripe wave solution,Whent→ ∞,the lump solution disappears,and only the stripe wave solution exists.It reflects the completely non-elastic interaction between two different waves.The process of interaction of lump solution is drowned or swallowed by stripe wave can be seen from Fig.4 and Fig.5.

4 Summary and Discussions

In summary,based on Horota bilinear form,we study the(2+1)-dimensional Sawada–Kotera equation.Lump solutions and mixed exponential-algebraic solitary wave solutions are obtained.The completely non-elastic interaction between lump solution and stripe solution for the(2+1)-dimensional Sawada–Kotera equation are presented. The dynamic behavior shows that the mixed exponential-algebraic solitary wave solution is instability.These results might be helpful to understand the propagation processes for nonlinear waves in fluid mechanics and enrich the variety of the dynamics of higher dimensional nonlinear wave field.

[1]B.G.Konopelchenko and V.G.Dubrovsky,Phys.Lett.A 102(1984)15.

[2]C.W.Cao and X.Yang,Commun.Theor.Phys.49(2008)31.

[3]X.Lü,Nonlinear Dyn.76(2014)161.

[4]Y.Q.Shi and D.L.Li,Computers Fluids 68(2012)88.

[5]X.Lü,B.Tian,K.Sun,and P.Wang,J.Math.Phys.51(2010)113506.

[6]C.Rogers,W.K.Schief,and M.P.Stallybrass,Int.J.Nonlinear Mechanics 30(1995)223.

[7]V.G.Dubrovsky and Y.V.Lisitsyn,Phys.Lett.A 295(2002)198.

[8]Y.H.Wang and Y.Chen,Commun.Theor.Phys.56(2011)672.

[9]S.Y.Lou,et al.,Acta.Phys.Sin.43(1994)1050.

[10]H.Y.Zhi and H.Q.Zhang,Commun.Theor.Phys.49(2008)263.

[11]H.Y.Zhi,Commun.Theor.Phys.51(2009)777.

[12]A.R.Adem and X.Lü,Nonlinear.Dyn.84(2016)915.

[13]A.M.Wazwaz,Math.Meth.Appl.34(2011)1580.

[14]Z.L.Zhao,Y.F.Zhang,and T.C.Xia,Abstr.Appl.Anal.2014(2014)1.

[15]S.V.Manakov,V.E.Zakharov,and L.A.Bordag,et al.,Phys.Lett.A 63(1977)205.

[16]J.Satsuma and M.J.Ablowitz,J.Math.Phys.20(1979)1496.

[17]D.J.Kaup,J.Math.Phys.22(1981)1176.

[18]K.Imai,Prog.Theor.Phys.98(1997)1013.

[19]W.X.Ma,Phys.Lett.A 379(2015)1975.

[20]W.X.Ma,Z.Qin,and X.Lü,Nonlinear Dyn.84(2016)923.

[21]H.C.Ma and A.P.Deng,Commun.Theor.Phys.65(2016)546.

[22]X.Lü and W.X.Ma,Nonlinear Dyn.85(2016)1217.

[23]A.S.Fokas,D.E.Pelinovsky,and C.Sulem,Physica D:Nonlinear Phenomena 152(2001)189.

[24]Z.M.Lu,E.M.Tian,and R.Grimshaw,Wave Motion 40(2004)123.

[25]L.L.Huang and Y.Chen,Appl.Math.Lett.64(2017)177.

[26]C.J.Wang,Z.D.Dai,and C.F.Liu,Mediterr.J.Math.13(2016)1087.

[27]W.Tan and Z.D.Dai,Nonlinear Dyn.85(2016)817.

[28]V.A.Vladimirov and C.Maczka,Rep.Math.Phys.60(2007)317.

[29]M.C.Nucci,J.Phys.A:Math.Gen.22(1989)2897.

[30]R.Hirota,The Direct Method in Soliton Theory,Cambridge University Press,Cambridge(2004).