Reciprocal transformations of the space–time shifted nonlocal short pulse equations
Jing Wang(王靜), Hua Wu(吳華), and Da-Jun Zhang(張大軍)
Department of Mathematics,Shanghai University,Shanghai 200444,China
Keywords: reciprocal transformation, space–time shifted nonlocal short pulse equation, covariance of variable,solution
1. Introduction
Reciprocal transformation is a technique used to transform nonlinear partial differential equations into other partial differential equations. It consists of interchanging the dependent and independent variables. In particular, when the achieved equation is linear, the transformation is known as a hodograph transformation. Reciprocal transformations play useful roles in the research of nonlinear partial differential equations. One apparent advantage of reciprocal transformations is that in many cases these transformations give rise to a procedure of relating allegedly new equations to the rest of their equivalent integrable sisters. Thus, the objective equations can be studied by studying the integrable equations linked via reciprocal transformations. For more details about the introduction of reciprocal transformations and their application examples, one can refer to Ref. [1] and the references therein. Some remarkable integrable equations that are investigated by means of reciprocal transformations are the Camassa–Holm equation,[2]the Vakhnenko equation,[3]the (ultra-)short pulse equation,[4]the constant astigmatism equation,[5]etc. The short pulse(SP)equation,SP equation (1) allows both physical and mathematical twocomponent extension.[16–19]In this paper,the two-component form of our interest is[17,18]
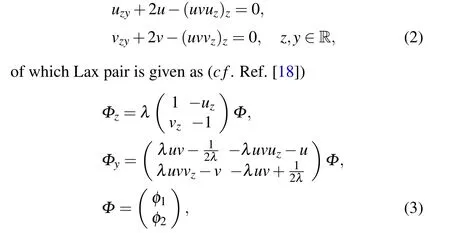

whereλz=λy= 0. The system (2) allows various reductions. For example,byu=δvit yields the SP equation(1);byu=δv?it yields a complex version of Eq.(1)(cf. Ref.[20]).It also allows nonlocal reductionsu(z,y) =δv(?z,?y) andu(z,y)=δv?(?z,?y), whereδ=±1 and?stands for complex conjugate.
Note that nonlocal reduction was first systematically introduced by Ablowitz and Mussilimani in 2013[21]and soon after nonlocal integrable systems received intensive attention from various aspects,e.g., Refs. [22–25]. More recently,Ablowitz and Mussilimani introduced space–time shifted nonlocal reductions.[56]For the SP system(2),via two space–time shifted nonlocal reductions

one can, respectively, obtain two nonlocal SP equations with space–time shifts:

provides a model to describe propagation of ultra-short pulses in nonlinear media with more accurate approximation.[4–6]Before the work,[4]this equation has been derived by Rabelo in 1987 as a pseudospherical-type equation.[7–9]It is integrable,characterized by theWadati–Konno–Ichikawa[10](WKI)spectral problem,[8,11]and related to the sine-Gordon equation or its non-potential form (known also as finite-amplitude baroclinic wave equations[12]or coupled integrable dispersionless equations[13])via reciprocal transformations.[11,14,15]The
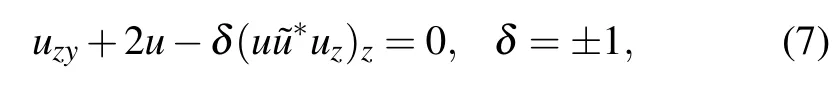
where ?u=u(z0?z,y0?y), (z,y) are real coordinates, andz0,y0are real numbers.
Since reciprocal transformations mix dependent and independent variables and to recover the independent variables of the investigated equation one needs to make use of integration,the research will become complicated once a reverse space?xis involved. In a recent paper,[41]covariance of dependent and independent variables in the reciprocal transformation of the nonlocal vector SP system was discussed. It can be imagined that the reciprocal transformation will be more complicated when space–time shifts are involved in nonlocal cases.
In this paper, with Ref. [41] as a pre-research, we will focus on the following:to elaborate the reciprocal transformations and the covariance of variables for the space–time shifted nonlocal SP equations(6)and(7);to present solutions in double Wronskian form for these two equations; and to present conditions that guarantee the realness of (z,y) in the reciprocal transformations.
This paper is organized as follows. In Section 2,we elaborate reciprocal transformation for the space–time shifted nonlocal SP equations and the covariance of variables involved in the transformation. Then in Section 3 we present double Wronskian solutions to the the space–time shifted nonlocal SP equations,and investigate the realness of independent variablez. As examples,dynamics of two obtained solutions are illustrated. Finally,conclusions are given in Section 4.
2. Nonlocal reciprocal transformation and covariance of variables

Let us consider the negative order Ablowitz–Kaup–Newell–Segur(AKNS)equation(AKNS(?1)for short)[57]Then, it can be verified that the first two equations in Eq.(9)are converted to the coupled SP system(2).
The AKNS(?1)system(8)allows two space–time shifted nonlocal reductions,

and then from Eq.(16)we can verify that


In other words, the space–time shifted nonlocal reduction(4)holds, which means the reciprocal transformation (10) together with Eq.(16)does convert the space–time shifted nonlocal AKNS(?1) equation (14) into the space–time shifted nonlocal SP equation(6).
For the complex reduction(13),one has

and the covariant correspondence(19)as well,from which the relation(5)holds and equation(15)is converted to Eq.(7).
Note thatzandydefined by Eq.(17)must be real. This will be elaborated in the next section after we present explicit solutions of the nonlocal equations(14)and(15).
3. Solutions
In this section, we first begin with by presenting double Wronskian solutions for the unreduced AKNS(?1)system(8)as well as for the coupled SP system (2). Next, by means of a reduction technique,solutions of the reduced equations(14)and (15) will be derived. After that, we will check the realness of the independent variablez(x,t) defined in Eq. (17).Then, solutions to the reduced SP equations (6) and (7) will be achieved via Eqs. (11) and (17). Finally, as examples, we will also give explicit one-soliton solution and breather solution with illustrations for the space–time shifted nonlocal SP equation(6).
3.1. Solutions to the unreduced AKNS(?1)system(8)and SP system(2)
The AKNS(?1)system(8)admits bilinear forms[57]


It is notable that matrixAand any matrix similar to it lead to the sameqandr. Then, with the transformation (21) and Wronskians(22),and in light of the reciprocal transformations between the AKNS(?1) system (8) and the coupled SP system (2) that we have described in the previous section, one can find that the unreduced SP system(2)admits solutions

3.2. Solutions to the reduced SP equations(6)and(7)
Note that the reduction technique based on bilinear form and double Wronskians was first developed in Refs. [32,33]and has proved effective in deriving solutions for nonlocal integrable equations,[34,41,42,51,60–63]including the discrete[34]and space–time shifted nonlocal cases[63]as well. The main idea of this technique is to impose certain constraints on matrixAand column vectorψin double Wronskian solution of the unreduced system,such that the defined functionsqandr(oruandv)satisfy desired reductions. In the following,let us directly present solutions for the reduced equations.
Theorem 1 Assume



which indicates the reduction (13) holds. One can refer to Ref.[63]which contains similar details.
Note that nonlocal equations with shifted space and time have also been studied based on Hirota’s bilinear forms and low order soliton (e.g., 1-soliton and 2-soliton) solutions can be explicitly presented in terms of exponential polynomials.[64]
3.3. Explicit form of solutions and realness of z(x,t)
For the sake of consistency of reduction,the independent variablezdefined in Eq.(25b)must be real. In the following,we present explicit form of?andψwith which we can clarify the realness ofz.
Following the treatment in Ref.[32], we considerTandAof the following block matrix form
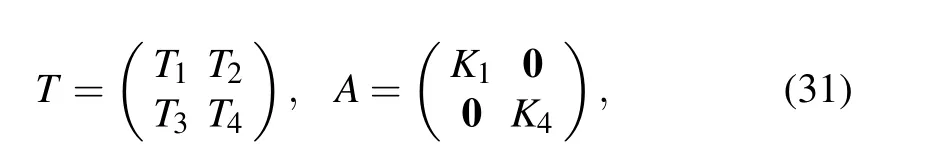
and list out solutions of Eqs.(27b)and(28b)in Table 1,whereTiandKiare(N+1)×(N+1)matrices,IN+1is the identity matrix of orderN+1 and i2=?1.
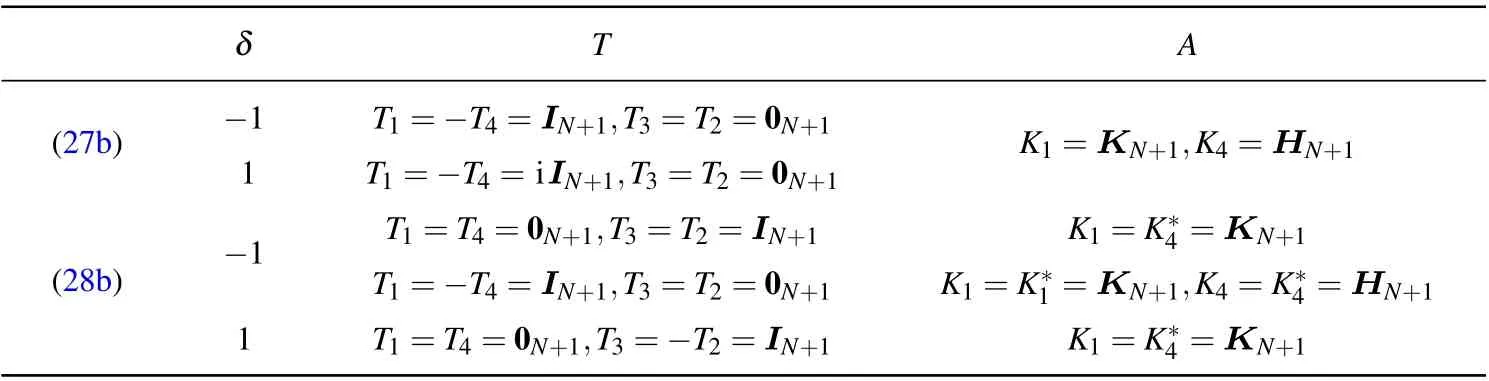
Table 1. T and A for constraints(27b)and(28b).

The realness ofzdefined by Eq. (25b) can be guaranteed byf=ε f?,whereε=±1.


whereci,ki ∈C,η(k)=?kx?t/4k;whenKN+1=JN+1(k),?takes the form
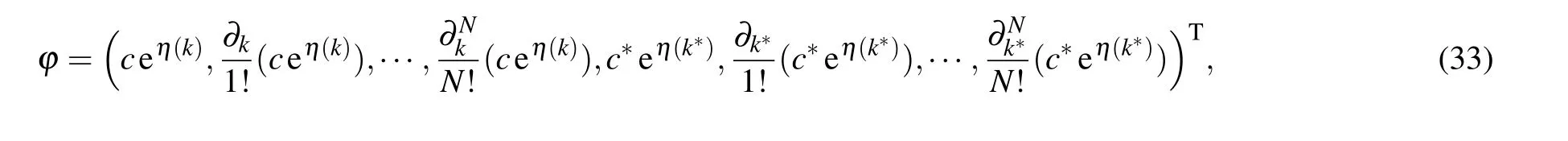
wherec,k ∈C.
Note that there can be more choices for case(27)to have a realz. For example,one may takeA=Diag(k1,k2,h1,h2)wherek1,k2∈R andh1=h?2∈C.
3.4. Examples
As an example we investigate dynamics of the space–time shifted nonlocal SP equation(6)withδ=?1,i.e.,wherek1,h1∈R ork1=h?1∈C. Consider a special case where takingk1=?h1∈R,and then we have



Fig. 1. (a) Profile of 1-antiloop soliton solution u given by Eq. (36) for k1=?1,x0=?1,t0=?1. (b)Profile of 1-loop soliton solution u given by Eq.(36)for k1=1,x0=?1,t0=?1.

One can see thatucontains two different phasesθ1andθ2,of which the former governs the envelope of the breather while the latter characterizes the internal oscillation, as depicted in Fig.2.

Fig. 2. Profile of 1-breather solution u given in Eq. (37) for a = 0.4,b=?0.8,x0=1,t0=1.
4. Conclusions
In this paper we have elaborated the reciprocal transformations that convert the space–time shifted AKNS(?1)equations(14)and(15)to the space–time shifted nonlocal SP equations(6)and(7),explained covariance of variables,presented double Wronskian solutions,clarified realness of the independent variablez, and illustrated some obtained solutions. Because the nonlocal integrable systems introduced by Ablowitz and Musslimani[22]have drawn intensive attention, the SPtype equations are a special type of integrable systems,and in nonlocal case reciprocal transformations become more complicated,thus the investigation of this paper is significant.
Acknowledgement
Project supported by the National Natural Science Foundation of China(Grant Nos.11875040 and 12171308).
- Chinese Physics B的其它文章
- Fault-tolerant finite-time dynamical consensus of double-integrator multi-agent systems with partial agents subject to synchronous self-sensing function failure
- Nano Ag-enhanced photoelectric conversion efficiency in all-inorganic,hole-transporting-layer-free CsPbIBr2 perovskite solar cells
- Low-voltage soft robots based on carbon nanotube/polymer electrothermal composites
- Parkinsonian oscillations and their suppression by closed-loop deep brain stimulation based on fuzzy concept
- Temperature dependence of spin pumping in YIG/NiO(x)/W multilayer
- Interface effect on superlattice quality and optical properties of InAs/GaSb type-II superlattices grown by molecular beam epitaxy

