RIGIDITY OF COMPACT SURFACES IN HOMOGENEOUS 3-MANIFOLDS WITH CONSTANT MEAN CURVATURE?

Jing WANG(王靜)

School of Mathematics and Statistics,Beijing Institute of Technology,Beijing 100081,China

Yinshan ZHANG(張銀山)?

School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China

RIGIDITY OF COMPACT SURFACES IN HOMOGENEOUS 3-MANIFOLDS WITH CONSTANT MEAN CURVATURE?

Jing WANG(王靜)

School of Mathematics and Statistics,Beijing Institute of Technology,Beijing 100081,China

E-mail:wangjingzzumath@163.com

Yinshan ZHANG(張銀山)?

School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China

E-mail:zhangysookk@163.com

In this paper,we establish a rigidity theorem for compact constant mean curvature surfaces of the Berger sphere in terms of the surfaces’geometric invariants.This extends the previous similar result on compact minimal surfaces of the Berger sphere.

homogeneous 3-manifolds;Berger sphere;constant mean curvature surface; Hopf torus;Cliford torus

2010 MR Subject Classifcation53C24;53C20;53C42

1 Introduction

This paper is a continuation of Hu-Lyu-Wang’s previous work[1].According to the standard notation,we denote by E(κ,τ)the homogeneous 3-manifolds whose isometry group is of dimension 4,where κ and τ are constant and κ 6=4τ2.In[1]the authors studied surfaces of E(κ,τ)and,as main results,rigidity theorems in terms of the second fundamental form are established for compact minimal surfaces of the Berger sphere S3b(κ,τ)(κ 6=4τ2).In this paper, by checking the proof of[1]in further detail,we succeed in extending the rigidity theorem therein to all compact surfaces of S3b(κ,τ)(κ 6=4τ2)with constant mean curvature.

We noticed that,in the last years the study of constant mean curvature surfaces of the homogeneous Riemannian 3-manifolds is a topic of increasing interest,see[2–11]and references therein.

Recall that for E(κ,τ),equipped with a Riemannian metric g that also denoted by h·,·i, there exists a Riemannian submersion Π:E(κ,τ)→M2(κ),where M2(κ)is a 2-dimensional simply connected space form of constant curvature κ,with totally geodesic fbers and there exists a unit Killing vector feld ξ on E(κ,τ)which is vertical with respect to Π.The bundle curvature is the number τ such thatfor any vector feldwhere×denotes the vector product and?denotes the Riemannian connection of E(κ,τ),respectively. When τ=0(and then κ 6=0),we get a product manifold M2(κ)×R,the vertical vector ξ is tangent to the factor R.This case was treated extensively,we refer to [12],among many others.The manifolds with τ 6=0 are of three types based on the value of κ:the Berger spheres for κ>0 that is commonly denoted by S3b(κ,τ);the Heisenberg group Nil3for κ=0;and the universal coverfSL(2,R)of the Lie group SL(2,R)(endowed with a 2-parameter family of homogeneous metrics)for κ<0.

To state our results,let Φ:Σ→ E(κ,τ)be an immersion of a surface Σ,and denote by C,H and S the angle function,the mean curvature and the squared norm of the second fundamental form of Φ,respectively(see Section 2 for the defnition of C,H and S).Then the main result of[1]can be stated as

Theorem 1.1(see[1]) Let Φ:Σ→E(κ,τ)be a minimal immersion of a compact surface Σ.Then it holds the Simons’type integral inequality

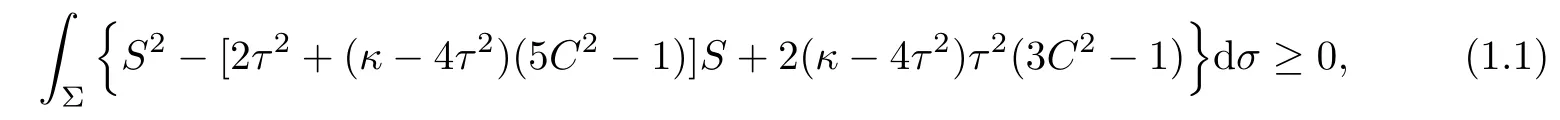
where the equality holds if and only if Φ is of parallel second fundamental form.

In particular,if Φ:Σ→S3b(κ,τ)(κ 6=4τ2)is a minimal immersion of a compact surface Σ,then equality holds in(1.1)if and only if Φ:Σ→S3b(κ,τ)is the Cliford torus,the latter case occurs only when C≡0 and S≡2τ2.

To prove Theorem 1.1,due to that E(κ,τ)is of no constant sectional curvature,instead of computing the Laplacian of the squared norm of the second fundamental form?S alone as one usually did when studying minimal surfaces of the unit sphere S3(1),a computation of the combination?S?(κ?4τ2)[?|T|2?2div(?TT)]was carried out,here T denotes the tangential component of the Killing feld ξ onto the surface.

Conceptually,one expects that the rigidity phenomena of Theorem 1.1 can be extended to all surfaces of E(κ,τ)with constant mean curvature.We fnd,however,if we deal again with the combination?S?(κ?4τ2)[?|T|2?2div(?TT)]in the situation of non-minimal constant mean curvature surfaces,it turns out impossible.Eventually,we fnd that the right way is to compute?S?(κ?4τ2)?|T|2.Accordingly,in this paper we can extend Theorem 1.1 to achieve the following main conclusion.

Theorem 1.2Let Φ:Σ→E(κ,τ)be a constant mean curvature immersion of a compact surface Σ.Then it holds the Simons’type integral inequality

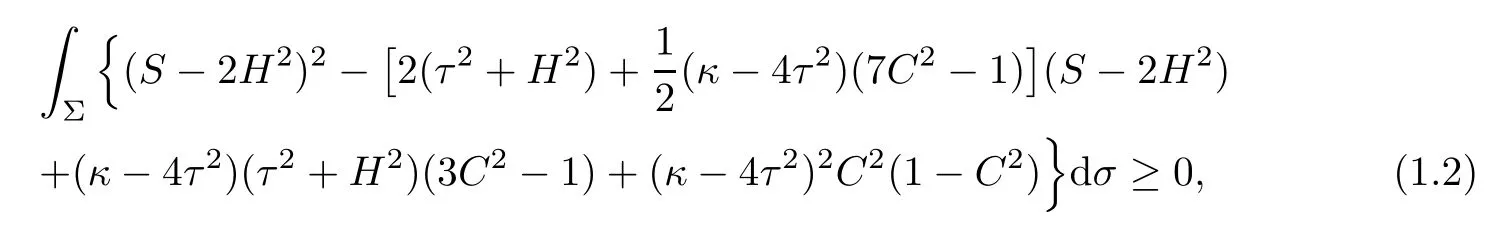
where the equality holds if and only if Φ is of parallel second fundamental form.

In particular,if Φ:Σ→S3b(κ,τ)(κ 6=4τ2)is a constant mean curvature immersion of a compact surface Σ,then equality holds in(1.2)if and only if Φ:Σ→S3b(κ,τ)is the Cliford torus,the latter case occurs only when C≡0 and S≡2τ2+4H2.

As a counterpart of Theorem 1.1,from Theorem 1.2 we immediately have the following.

Corollary 1.3Let Φ:Σ→ E(κ,τ)be a minimal immersion of a compact surface Σ.

Then it holds the Simons’type integral inequality

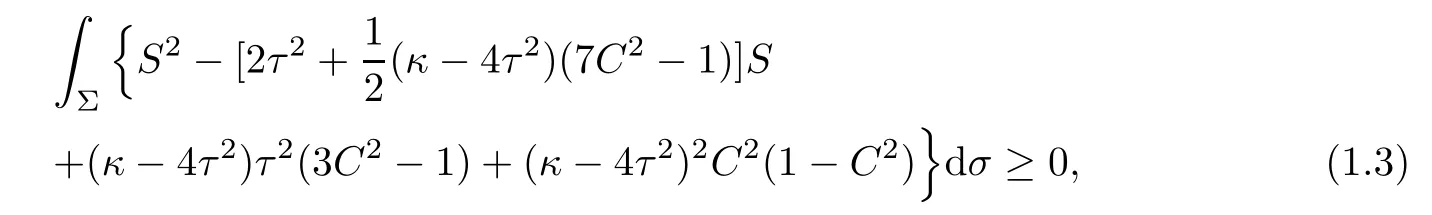
where the equality holds if and only if Φ is of parallel second fundamental form.

In particular,if Φ:Σ→S3b(κ,τ)(κ 6=4τ2)is a minimal immersion of a compact surface Σ,then equality holds in(1.3)if and only if Φ:Σ→S3b(κ,τ)is the Cliford torus,the latter case occurs only when C≡0 and S≡2τ2.

Remark 1.4It is well known that,for a compact immersed surface M of the unit sphere S3(1)with constant mean curvature H,the squared norm S of its second fundamental form satisfes the Simons’integral inequality

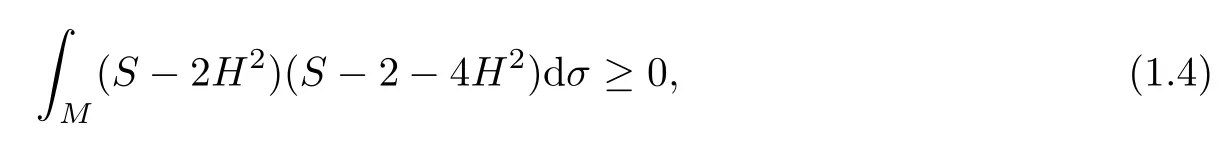
where the equality holds if and only if M is either the totally umbilic sphere or the Cliford torus(see[13,14]).Compared the diference between(1.2)for S3b(κ,τ)and(1.4)for S3(1),it is remarkable that the equality sign in(1.2)is attainable only by the Cliford torus.This can be convinced by the conclusion that there exists no totally umbilic surfaces in S3b(κ,τ)(κ 6=4τ2) (see[15]).

2 Preliminaries

Following[16],we made the following convention that the Riemannian curvature tensor R of E(κ,τ)is defned by

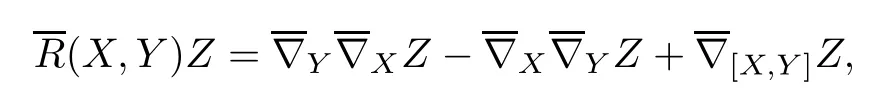
where X,Y,Z are tangent vector felds of E(κ,τ).Then we have

Proposition 2.1(see[16]) For all vector felds X,Y,Z,W on E(κ,τ),we have

It follows that

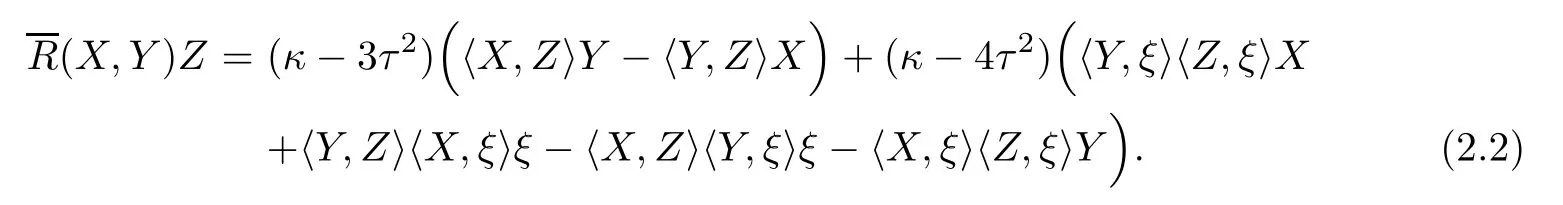
Let Φ:Σ→E(κ,τ)be an immersion of oriented surface Σ and?be the induced Riemannian connection on Σ.We choose a local feld of orthonormal positively frames{e1,e2;e3}in E(κ,τ)such that,restricted to Σ,the vectors e1,e2are tangent to Σ and e3is normal to Σ.Let {ωA}1≤A≤3be the dual frame feld of{eA}1≤A≤3.For brevity,we use the following convention on the range of indices unless otherwise stated:1≤A,B,C,···≤3;1≤i,j,k,···≤2.Thenthe structure equations of E(κ,τ)are given by

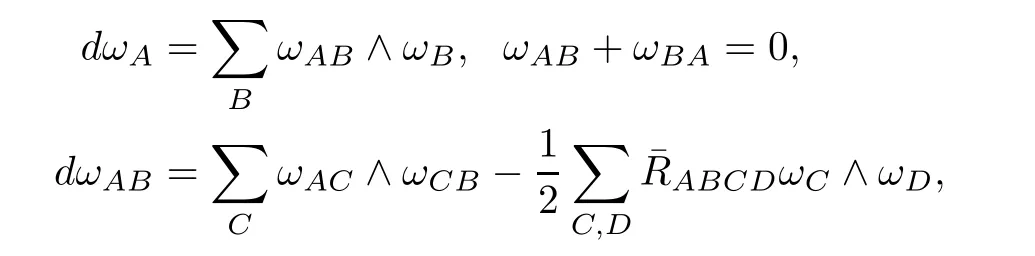
where RABCD=hR(eA,eB)eC,eDi are the components of R.

When restricted to Σ,we have ω3=0 and ωi3=Pjhijωj,hij=hji.

The second fundamental form h,the mean curvature H and the squared norm S of h are given by

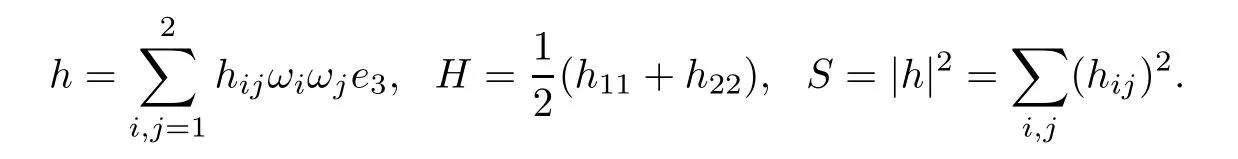
The frst and second covariant derivatives hijkand hijklof hijare thus defned by

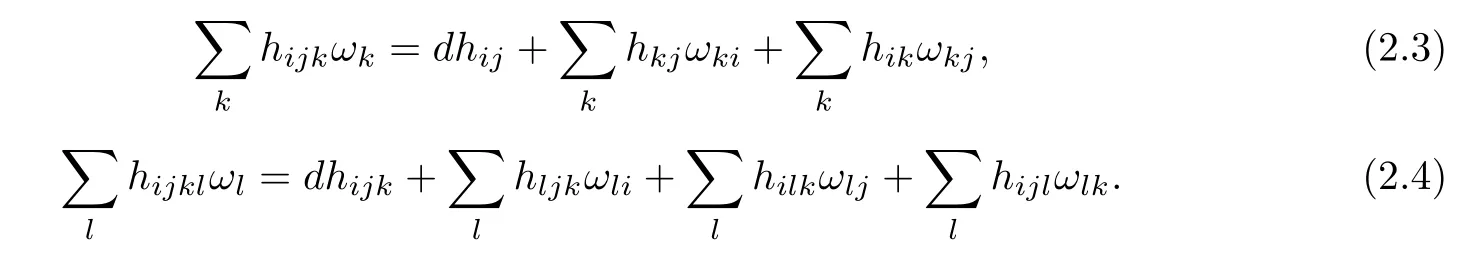
Denote C=he3,ξi,which is called the angle function of Φ:Σ→E(κ,τ).Put

Let Rijklbe the components of the Riemannian curvature tensor R of Σ,which is given by

From these we obtain the Gauss equation of Φ:Σ→E(κ,τ),

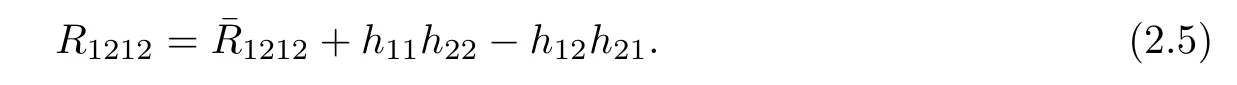
Let K=R1212denote the Gauss curvature of Σ,then by applying(2.1)we can write(2.5) to be(see also[16])

Similarly,we can derive the Codazzi equation of Φ:Σ→E(κ,τ),

and the Ricci identity

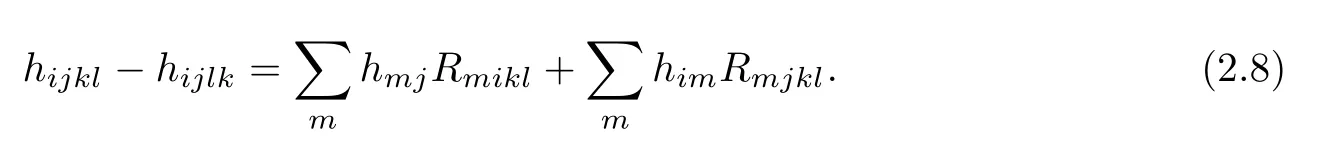
At any fxed point p∈Σ,we can suitably choose the local orthonormal frame feld{e1,e2} such that hij(p)=λiδij.If not stated otherwise,all calculations in sequel is carried out at p.

Put dC=PiCiωi.Then we have

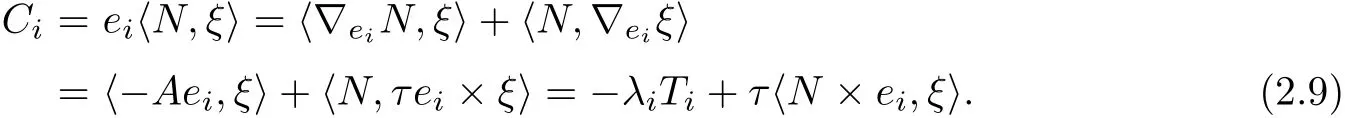
We need to calculate Ti,jfor later use,

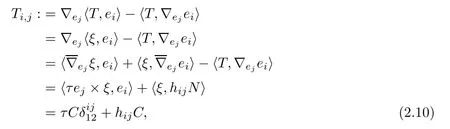
3 Lemmas and Their Proofs

First of all,we recall the following Simons’type formula for surfaces in E(κ,τ),which we have derived in[1]by using the Gauss-Codazzi equations and the Ricci identity.

Lemma 3.1(see[1]) Let Φ:Σ→ E(κ,τ)be an immersion of a surface Σ.Then,at p∈Σ,it holds

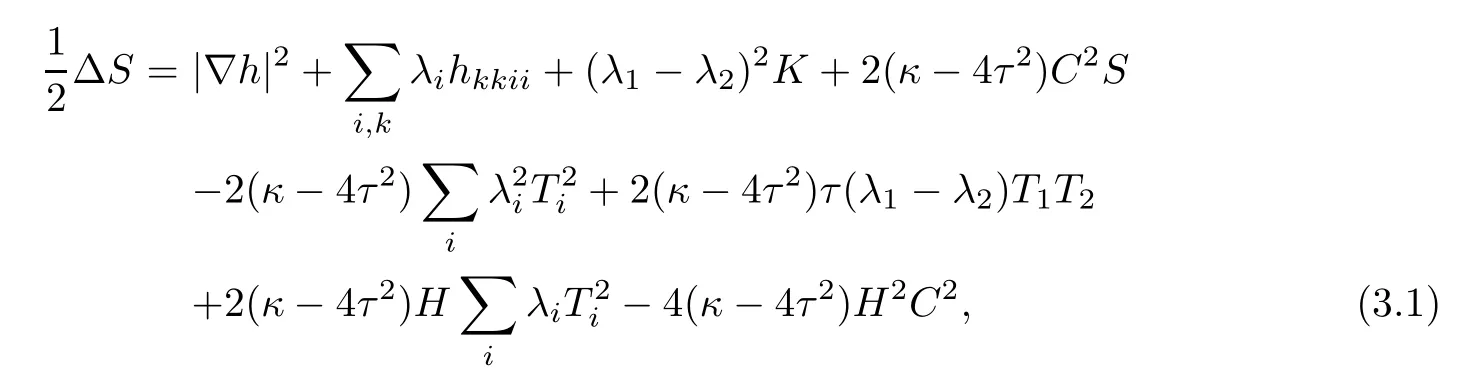
where?denotes the Laplacian of the induced metric on Σ.

Lemma 3.2(see[1]) Let Φ:Σ→ E(κ,τ)be an immersion of a surface Σ.Then,at p∈Σ,it holds that

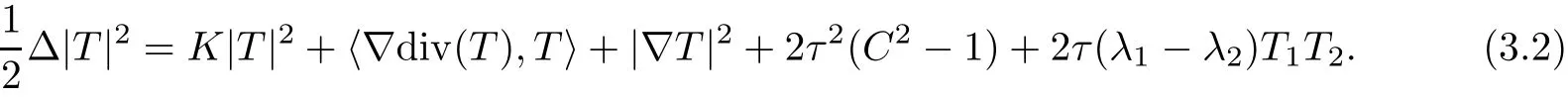
To deal with surfaces Φ:Σ→E(κ,τ)of constant mean curvature H,we have improved the above two Lemmas when restricted to the case H=0 in[1].In fact,such improvement can be extended to all H 6=0 cases to meet our subsequent requirements.

Lemma 3.3Let Φ:Σ→E(κ,τ)be constant mean curvature immersion of a surface Σ. Then,at p∈Σ,it holds that

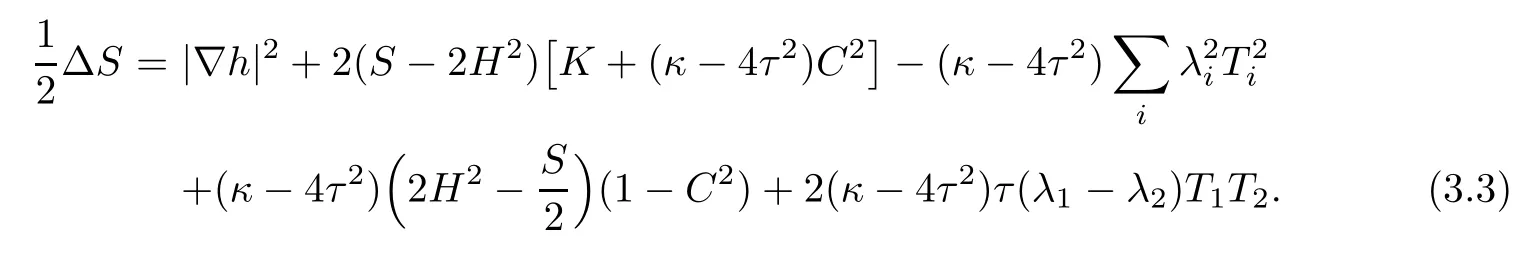
ProofThis is an direct consequence of(3.1).

In fact,frst using that H is constant,we obtain that

Further,noting that|T|2=1?C2,λ1λ2=2H2?S2and(λ1?λ2)2=2(S?2H2),we canwrite

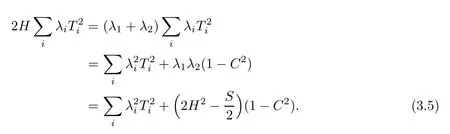
Inserting(3.4)and(3.5)into(3.1),we immediately get assertion(3.3).

The calculation of?|T|2can also be improved to obtain the following.

Lemma 3.4Let Φ:Σ→E(κ,τ)be a constant mean curvature immersion of a surface Σ.Then,at p∈Σ,it holds that

ProofAccording to(2.9)and(2.10),we have

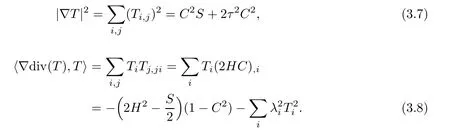
Inserting(3.7)and(3.8)into(3.2),we get assertion(3.6).

Now we state the main results of this section,which will be crucial for the proof of Theorem 1.2.

Lemma 3.5Let Φ:Σ→E(κ,τ)be a constant mean curvature immersion of a surface Σ.Then it holds on Σ that

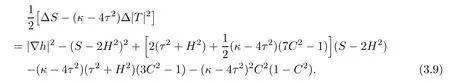
ProofAccording to Lemmas 3.3,3.4 and the Gauss equation(2.6),we see that(3.9) holds at p∈Σ.The assertion fnally follows from the fact that each term on both sides of(3.9) is independent of the choice of the orthonormal frame.

Remark 3.6To compare with Lemma 3.5,we recall that it was shown in[1]that for a minimal immersion Φ:Σ→E(κ,τ),the following holds on Σ:

We point out that if H is a non-zero constant,then we cannot extend the above computation so that the LHS of(3.10)still has an invariant form that is expressed in terms of the well-defned functions as we obtained on the RHS of(3.9).

4 Examples and Proof of Main Theorem

Let us frst look at the examples of the Cliford tori in the Berger spheres.

Recall that as a special case of E(κ,τ)for κ>0 and τ 6=0,the Berger sphere S3b(κ,τ)is the 3-sphere S3={(z,w)∈C2:|z|2+|w|2=1}endowed with the metric g=h,ibas that

where h,i0stands for the usual metric on the sphere,V(z,w):=(iz,iw)for each(z,w)∈S3.

The above relation between the standard metric on the sphere and the Berger metric immediately implies the next formula,that links the Levi-Civita connection?0of the round sphere to?,the one associated to the Berger metric(see[17]):

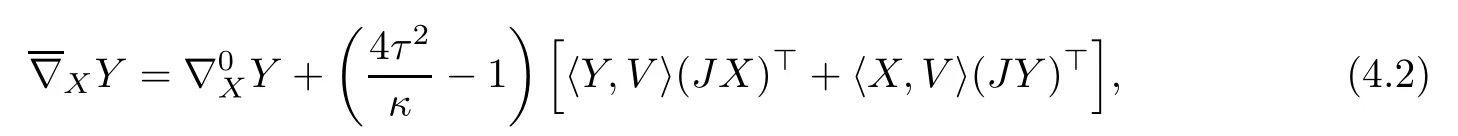
where J is the complex structure of C2,that is J(z,w)=(iz,iw),and()?denotes the tangential component to the sphere.

The Hopf fbration Π:S3b(κ,τ)→ S2(κ),where S2(κ)stands for the 2-sphere of radius 1/√κ,defned by

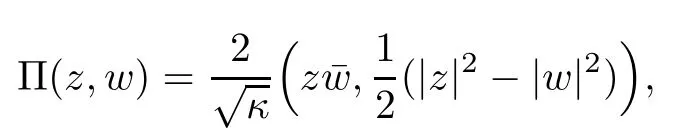
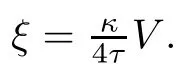
By defnition,the Cliford tori are a family surfaces of the Berger sphere which can be parameterized by φ(r1,r2):R2→S3b(κ,τ)with

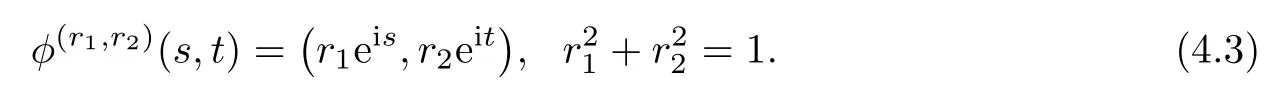
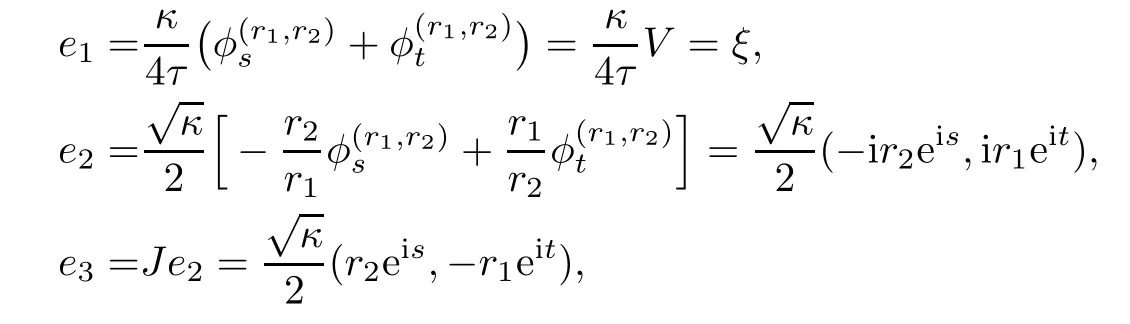
we see that{e1,e2;e3}is a local orthonormal frame of S3b(κ,τ),and e1,e2are tangent vector felds of φ(r1,r2)(R2),e3is its normal vector feld.Let{ωA}1≤A≤3be the dual frame feld ofThe fact thatis a Hopf torus can now be seen from the fact thatis a unit tangent vector feld of φ(r1,r2)(R2).Straightforward computation by using(4.2)gives that

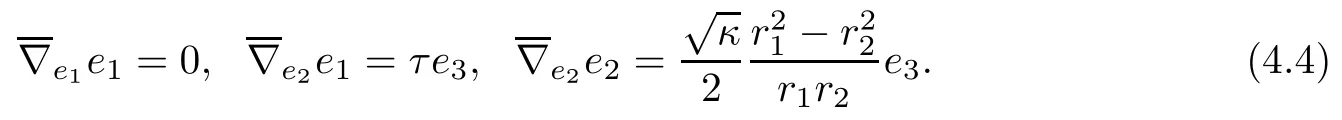
Let ωABbe the connection forms associated to{e1,e2;e3},then(4.4)implies that

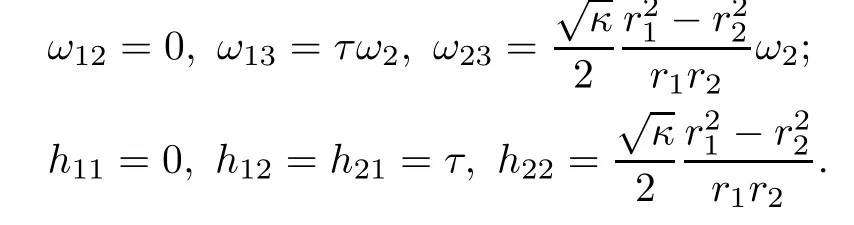
In addition,from the above calculations and(2.3),we can immediately obtain that hijk=0 for all i,j,k.Hence the Cliford tori are of parallel second fundamental form.

We also need the following simple observation.

Proposition 4.1Let Φ:Σ→E(κ,τ)(τ 6=0)be a constant mean curvature immersion of a compact surface Σ.Then the angle function C≡0 is equivalent to that the squared norm of the second fundamental form of Φ satisfes S≡2τ2+4H2.

ProofIf C≡0,then the Gauss equation(2.6)implies that

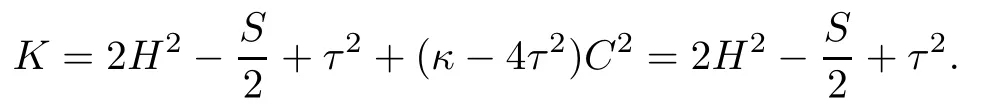
On the other hand,C≡0 showing that ξ is a tangent vector feld of Σ.Thus,for a tangent vector feld v,?vξ=τv×ξ∈T⊥Σ.This implies that?vξ=0 and therefore R(v,ξ,ξ,v)=0. Hence we have K≡0,and then S≡2τ2+4H2follows.

The converse follows from the following integral formula(see(3.3)in[18]):

In fact,if S≡2τ2+4H2,then the Gauss equation(2.6)gives that K=(κ?4τ2)C2.From (4.5),we obtain

Therefore,C2(1?C2)=0 on Σ.The following remark shows that C2=1 does not occur,we get C=0 on Σ as claimed.

Remark 4.2As pointed out in[18],if C2=1,then it is well known that τ=0 and the surface is a totally geodesic slice of M2(κ)×R.This holds true even without the compactness assumption.

Finally,before giving the proof of Theorem 1.2,we noticed that surfaces with parallel second fundamental form in Bianchi-Cartan-Vranceanu spaces are shown to be the Hopf cylinders by Belkhelfa,Dillen and Inoguchi in[19].This particularly implies the following.

Theorem 4.3(see Theorem 8.2 of[19]) Let Φ:Σ→E(κ,τ)(τ 6=0)be a surface with parallel second fundamental form,then Φ is a Hopf cylinder.

Proof of Theorem 1.2Integrating(3.9)over Σ and using the divergence theorem,we immediately obtain the frst assertion.Then,the second assertion is a direct consequence of Theorem 4.3,Proposition 4.1 and a fact that the Hopf torus Φ(Σ)in S3b(κ,τ)has constant mean curvature if and only if Φ(Σ)is given by Π?1(γ)such that the cross closed curve γ in S2(κ) is of constant curvature(see[20]),which show that γ is a circle in S2(κ)and thus Φ(Σ)is a Cliford torus. ?

Remark 4.4In contrast with the above fact that the Cliford tori are the only constant mean curvature Hopf torus in S3b(κ,τ),an interesting phenomenon being worth noting is that in[18],it was shown that the only fat compact surfaces in S3b(κ,τ)are the Hopf tori.This later result in the Berger sphere contrasts with the case of the round sphere where,besides the Hopf tori,there are other fat tori(see[21,22]).

To get more explicit information from Theorem 1.2,we next consider the cases of Berger sphere S3b(κ,τ).For such cases and under some additional conditions,e.g.if κ>4τ2and,the following equation on x=S?2H2:

has two distinct real number solutions x1=a(κ,τ,C)and x2=b(κ,τ,C),where by letting

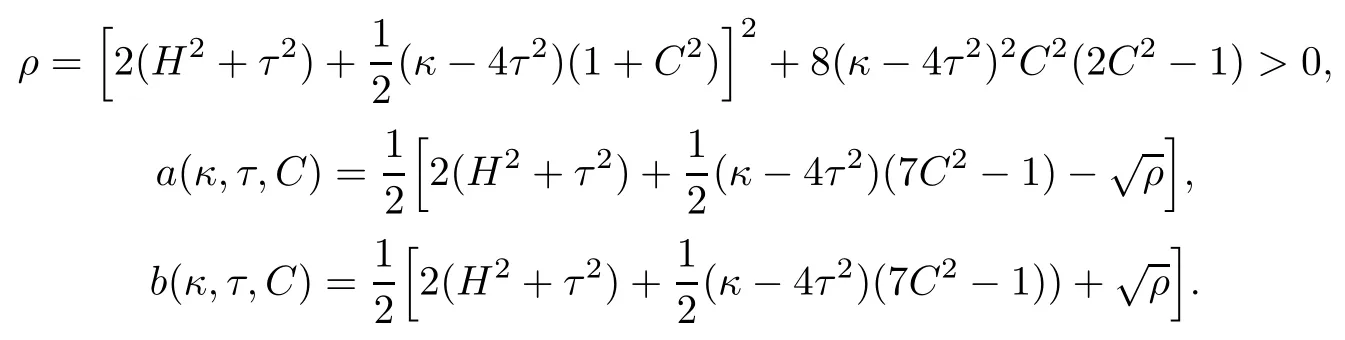
Combining Theorem 1.2 with the above discussions,we immediately get

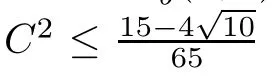
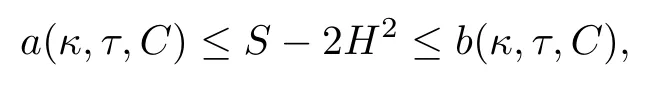
then it must be the case that C≡0,S≡2τ2+4H2and Φ is the Cliford torus.

[1]Hu Z,Lyu D,Wang J.On rigidity phenomena of compact surfaces in homogeneous 3-manifolds.Proc Amer Math Soc,2015,143:3097–3109

[2]Abresch U,Rosenberg H.A Hopf diferential for constant mean curvature surfaces in S2×R and H2×R. Acta Math,2004,193:141–174

[3]Abresch U,Rosenberg H.Generalized Hopf diferentials.Mat Contemp,2005,28:1–28

[4]Caddeo R,Piu P,Ratto A.SO(2)-invariant minimal and constant mean curvature surfaces in 3-dimensional homogeneous spaces.Manuscripta Math,1995,87:1–12

[5]Espinar J M,Rosenberg H.Complete constant mean curvature surfaces in homogeneous spaces.Comment Math Helv,2011,86:659–674

[6]Fernandez I,Mira P.A characterization of constant mean curvature surfaces in homogeneous 3-manifolds. Diferential Geom Appl,2007,25:281–289

[7]Inoguchi J,Van der Veken J.A complete classifcation of parallel surfaces in three-dimensional homogeneous spaces.Geom Dedicata,2008,131:159–172

[8]Meeks III W H,P′erez J.Constant mean curvature surfaces in metric Lie groups.Geometric analysis:partial diferential equations and surfaces//Contemp Math 570.Providence,RI:Amer Math Soc,2012:25–110

[9]Torralbo F.Rotationally invariant constant mean curvature surfaces in homogeneous 3-manifolds.Diferential Geom Appl,2010,28:593–607

[10]Torralbo F,Urbano F.Compact stable constant mean curvature surfaces in homogeneous 3-manifolds. Indiana Univ Math J,2012,61:1129–1156

[11]Jleli M.Stability of Constant mean curvature hypersurfaces of revolution in hyperbolic space.Acta Math Sci,2013,33B(3):830–838

[12]Daniel B.Isometric immersions into Sn×R and Hn×R and applications to minimal surfaces.Trans Amer Math Soc,2009,361:6255–6282

[13]Alencar H,do Carmo M.Hypersurfaces with constant mean curvature in sphere.Proc Amer Math Soc, 1994,120:1223–1229

[14]Xu H.A rigidity theorem for submanifolds with parallel mean curvature in a sphere.Arch Math,1993,61: 489–496

[15]Souam R,Toubiana E.Totally umbilic surfaces in homogeneous 3-manifolds.Comment Math Helv,2009, 84:673–704

[16]Daniel B.Isometric immersions into 3-dimensional homogeneous manifolds.Comment Math Helv,2007, 82:87–131

[17]Torralbo F.Compact minimal surfaces in the Berger spheres.Ann Global Anal Geom,2012,41:391–405

[18]Torralbo F,Urbano F.On the Gauss curvature of compact surfaces in homogeneous 3-manifolds.Proc Amer Math Soc,2010,138:2561–2567

[19]Belkhelfa M,Dillen F,Inoguchi J.Surfaces with parallel second fundamental form in Bianchi-Cartan-Vranceanu spaces.Banach Center Publ,2002,57:67–87

[20]Barros M,Ferr′andez A.Willmore energy estimates in conformal Berger sphere.Chaos Solitons Fractals, 2011,44:515–521

[21]Pinkall U.Hopf tori in S3.Invent Math,1985,81:379–386

[22]Weiner J L.Flat tori in S3and their Gauss maps.Proc London Math Soc,1991,62:54–76

?Received July 25,2015;revised March 28,2016.This work was supported by NSFC(11371330).

?Corresponding author:Yinshan ZHANG.