PROPERTIES OF THE MODIFIED ROPER-SUFFRIDGE EXTENSION OPERATORS ON REINHARDT DOMAINS?
Chaojun WANG(王朝君)Yanyan CUI(崔艷艷)
College of Mathematics and Statistics,Zhoukou Normal University,Zhoukou 466001,China
Hao LIU(劉浩)?
College of Mathematics and Statistics,Henan University,Kaifeng 475001,China
PROPERTIES OF THE MODIFIED ROPER-SUFFRIDGE EXTENSION OPERATORS ON REINHARDT DOMAINS?
Chaojun WANG(王朝君)Yanyan CUI(崔艷艷)
College of Mathematics and Statistics,Zhoukou Normal University,Zhoukou 466001,China
E-mail:wang9907081@163.com;cui9907081@163.com
Hao LIU(劉浩)?
College of Mathematics and Statistics,Henan University,Kaifeng 475001,China
E-mail:haoliu@henu.edu.cn
In this paper,we mainly discuss the properties of the modifed Roper-Sufridge operators on Reinhardt domains.By the analytical characteristics and distortion results of subclasses of biholomorphic mappings,we conclude that the modifed Roper-Sufridge operators preserve the properties of S??(β,A,B),almost starlike mapping of complex order λ on ?n,p2,···,pn.Sequentially,we get that the modifed Roper-Sufridge operators preserve spirallikeness of type β and order α,strongly pirallikeness of type β and order α,almost starlikeness of order α on ?n,p2,···,pn.The conclusions provide a new approach to construct these biholomorphic mappings which have special geometric properties in several complex variables.
Roper-Sufridge operator;spirallike mappings;starlike mappings
2010 MR Subject Classifcation32A30;30C25
1 Introduction
The property of biholomorphic mappings is one of the most important objects of study in geometric function theory of several complex variables.Starlike mappings and convex mappings are the mappings discussed more.In recent years,many people discussed the subclasses or extensions of starlike mappings and convex mappings,such as almost spirallike mappings of order α and type β.It is easy to fnd specifc examples of these new subclasses or extensions in one complex variable,which will enable us to better study these mappings.While,it is very difcult to fnd specifc examples in several complex variables.
In 1995,Roper and Sufridge[1]introduced an operator
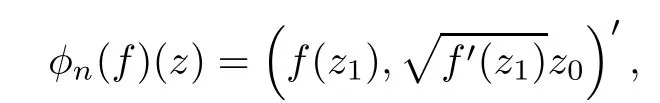
In 2005,Muir[6]introduced the generalized Roper-Sufridge operator

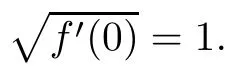

preserves almost starlikeness of order α and starlikeness of order α under some conditions on the unit ball Bn,where[f′(0)]1m=1 and P:Cn?1→C is a homogeneous polynomial of degree m(m∈N,m≥2).
Muir[9]introduced the extended Roper-Sufridge operator
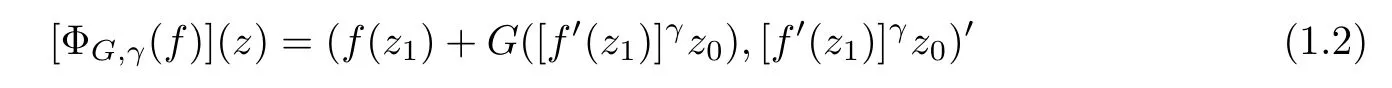
on the unit ball Bnin Cn,where z=(z1,z0)and f(z1)is a normalized univalent holomorphic function on D,G is a holomorphic function in Cn?1with G(0)=0,DG(0)=I,γ≥0 andThe homogeneous expansion of G(z)Qj(z),where Qj(z)is a homogeneous polynomial of degree j.Obviously,(1.2)reduces to(1.1)if γ=1mand j=m.Muir proved[ΦG,γ(f)](z)is a Loewner chain preserving extension operator provided that G satisfes some conditions.
In this paper,we mainly seek conditions under which the generalized operator(1.2)preserves the properties of subclasses of biholomorphic mappings.In Sections 2 and 3,we discuss (1.2)preserves the properties of S??(β,A,B),almost starlike mapping of complex order λ on?n,p2,···,pnunder diferent conditions,respectively.Thereby,we get that(1.2)preserves spirallikeness of type β and order α,strongly spirallikeness of type β and order α,almost starlikeness of order α on ?n,p2,···,pn.The conclusions generalize some known results.
In the following,let D denote the unit disk in C.Let JF(z)denote the Fr′echet derivative of F at z.Let I[a/b]denote the integer part ofab.
To get the main results,we need the following defnitions and lemmas.
Defnition 1.1(see[11]) Let ? be a bounded starlike and circular domain in Cn.The Minkowski functional ρ(z)of ? is C1except for a lower-dimensional manifold.Let F(z)be a normalized locally biholomorphic mapping on ?.If
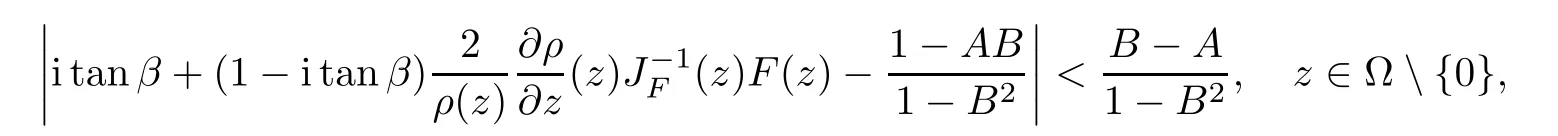
where?1≤A Setting A=?1=?B?2α,A=?B=?α,B→1?in Defnition 1.1,respectively,we obtain the corresponding defnitions of spirallike mappings of type β and order α[12],strongly spirallike mappings of type β and order α[13],almost spirallike mappings of type β and order α[14]on ?.For n=1,the condition in Defnition 1.1 reduces to Defnition 1.2(see[15]) Let ? be a bounded starlike and circular domain in Cn.The Minkowski functional ρ(z)of ? is C1except for a lower-dimensional manifold.Let F(z)be a normalized locally biholomorphic mapping on ?.If where λ∈C,Reλ≤0,F(z)is called an almost starlike mapping of complex order λ on ?. For n=1,the condition in Defnition 1.2 reduces to Lemma 1.3(see[9]) Let P(z)be a homogeneous polynomial of degree m,and let DP(z) be the Fr′echet derivative of P at z.Then Lemma 1.4(see[16]) Let ρ(z)(z 6=0)is the Minkowski functional ofThen where ProofSince then Let J?1F(z)F(z)=h(z)=(A,B)′,which follows that JF(z)h(z)=F(z).By Lemma 1.3,we have We can directly calculate that Thus,by Lemma 1.4 we can get the desired conclusion. Lemma 1.6(see[17]) Let ?∈Cnbe a bounded and complete Reinhardt domain.The Minkowski functional ρ(z)of ? is C1except for a lower-dimensional manifold ?0.Then for?z=(z1,···,zn)∈??0. Lemma 1.7(see[11]) Let f(z1)be a normalized biholomorphic function on D.Let and let l=max{p2,···,pn},m∈N,z∈?n,p2,···,pn,m≥l.Then Lemma 1.8(see[18]) If f(z)is a normalized biholomorphic function on the unit disk D, then In the following,let ?=?n,p2,···,pn,l=max{p2,···,pn},q=min{p2,···,pn}. Lemma 2.1(see[19]) Let f(z)be a holomorphic function on D with|f(z)|<1.Then Then (1)in the case of l∈[1,2],F(z)∈S??(β,A,B)provided that (i)for γ∈[0,16]we have (2)in the case of l∈(2,6),F(z)∈S??(β,A,B)provided that(i)holds for γ∈[0,16]and (ii)holds for γ∈(16,1l]; (3)in the case of l∈[6,+∞),F(z)∈S??(β,A,B)provided that(i)holds for γ∈[0,1l]. ProofBy Defnition 1.1,we need only to prove It is obvious that(2.1)holds for z0=0.For z06=0,let z=ζu=|ζ|eiθu,where u∈??n,p2,···,pnand ζ∈ˉD{0}.Then Since f(z1)∈S?D(β,A,B).By Defnition 1.1,we have Let Then|h(z1|<1 and By Lemma 2.1 we have By(2.1)we have By Lemma 1.5 and(2.2),(2.4),we have where By(2.3)and Lemmas 1.6,1.7,1.8,we have So,for?z1∈D,we have By(2.5)and(2.6),we obtain Since by(2.7)we have the following conclusions. (1)In the case of l∈[1,2], (i)for γ∈[0,16],if then we obtain Therefore which follows F(z)∈S??(β,A,B)by Defnition 1.1; we have the same conclusion to(i); we have the same conclusion to(i). (2)In the case of l∈(2,6),if(i)holds for γ∈[0,16]and(ii)holds for γ∈(16,1l],similar to(1)we have F(z)∈S??(β,A,B). (3)In the case of l∈[6,+∞),if(i)holds for γ∈[0,1l],similar to(1)we have F(z)∈S??(β,A,B). ? Setting γ=1mand j=m in Theorem 2.2,we get the following results. Corollary 2.3Let f(z1)∈S?D(β,A,B)with?1≤A Remark 2.4Setting A=?1=?B?2α and A=?B=?α in Theorem 2.2 and Corollary 2.3,respectively,we get the corresponding results for spirallike mappings of type β and order α,strongly pirallike mappings of type β and order α. Lemma 3.1(see[20]) Let p(z)be a holomorphic function on D such that p(0)=1 and Rep(z)>0,then Theorem 3.2Let f(z1)be an almost starlike function of complex order λ on D with λ∈C,Reλ≤0.Letbe the mapping denoted by(1.2)with (i)for γ∈[0,16]we have (ii)Qj=0(j>and for γ∈we have (iii)Qj=and for γ∈we have ProofBy Defnition 1.2,we need only to prove It is obvious that(3.1)holds for z0=0.Similar to Theorem 2.1,we obtain is the real part of a holomorphic function,so it is a harmonic function.By the minimum principle of harmonic functions,we need only to prove that(3.1)holds for z∈??n,p2,···,pn(z06=0).Thus ρ(z)=1. Since f(z1)is an almost starlike function of complex order λ on D.From Defnition 1.2, we have Let Then ?h(z1)>0,h(0)=1 and By Lemma 3.1,we have (3.2)follows that By Lemma 1.5 and(3.2),(3.4)we get where By(3.3)and Lemma 1.7,we have By(3.5),(3.6)and Lemma 1.8,we obtain we have Therefore which follows that F(z)is an almost starlike mapping of complex order λ on ?n,p2,···,pnby Defnition 1.2; (ii)for γ∈(16,12],if Qj=0(j>46γ?1)and then F(z)is an almost starlike mapping of complex order λ on ?n,p2,···,pnsimilar to(i); then F(z)is an almost starlike mapping of complex order λ on ?n,p2,···,pnsimilar to(i). (2)In the case of16<2qq2+l2<12,if(i)holds for γ∈[0,16]and(ii)holds for γ∈(16,2qq2+l2], then F(z)is an almost starlike mapping of complex order λ on ?n,p2,···,pnsimilar to(i). Corollary 3.3Let f(z1)be an almost starlike function of complex order λ on D with λ∈C,Reλ≤0.Let F(z)be the mapping denoted by(1.1)with m≥2.Then F(z)is an almost starlike mapping of complex order λ on ?n,p2,···,pnprovided that Remark 3.4Settingin Theorem 3.2 and Corollary 3.3,we get the corresponding results for almost starlike mappings of order α. [1]Roper K A,Sufridge T J.Convex mappings on the unit ball of Cn.J Anal Math,1995,65:333–347 [2]Graham I,Kohr G,Univalent mappings associated with the Roper-Sufridge extension operator.J Anal Math,2000,81:331–342 [3]Gong S,Liu T S,The generalized Roper-Sufridge extension operator.J Math Anal Appl,2003,284: 425–434 [4]Feng S X,Liu T S,The generalized Roper-Sufridge extension operator.Acta Math Sci,2008,28B:63–80 [5]Liu X S,Liu T S,On the generalized Roper-Sufridge extension operator for spirallike mappings of type β and order α.Chin Ann Math,2006,27A(6):789–798 [6]Muir J R.A modifcation of the Roper-Sufridge extension operator.Comput Methods Funct Theory,2005, 5(1):237–251 [7]Muir J R,Sufridge T J.Unbounded convex mappings of the ball in Cn.Trans Amer Math Soc,2001,129: 3389–3393 [8]Kohr G.Loewner chains and a modifcation of the Roper-Sufridge extension operator.Mathematica,2006, 71(1):41–48 [9]Muir J R.A class of Loewner chain preserving extension operators.J Math Anal Appl,2008,337(2): 862–879 [10]Wang J F,Liu T S.A modifcation of the Roper-Sufridge extension operator for some holomorphic mappings.Chin Ann Math,2010,31A(4):487–496 [11]Gao C L.The Generalized Roper-Sufridge Extension Operator on a Reinhardt Domain[D].Jinhua:Zhejiang Normal University,2012 [12]Liu X S,Feng S X.A remark on the generalized Roper-Sufridge extension operator for spirallike mappings of type β and order α.Chin Quart J of Math,2009,24(2):310–316 [13]Feng S X,Liu T S,Ren G B.The growth and covering theorems for several mappings on the unit ball in complex Banach spaces.Chin Ann Math,2007,28A(2):215–230 [14]Zhu Y C,Liu M S.The generalized Roper-Sufridge extension operator on Reinhardt domain Dp.Taiwanese Jour of Math,2010,14(2):359–372 [15]Zhao Y H.Almost Starlike Mappings of Complex Order λ on the Unit Ball of a Complex Banach Space[D]. Jinhua:Zhejiang Normal University,2013 [16]Zhang W J,Liu T S.On decomposition theorem of normalized biholomorphic convex mappings in Reinhardt domains.Science in China,2003,46(1):94–106 [17]Liu M S,Zhu Y C.Generalized Roper-Sufridge operators on bounded and complete Reinhardt domains. Science in China,2007,37A(10):1193–1206 [18]Duren P L.Univalent Functions.New York:Springer-Verlag,1983:57–58 [19]Ahlfors L V,Complex Analysis.3rd ed.New York:Mc Graw-Hill Book Co,1979 [20]Graham I,Kohr G.Geometric Function Theory in One and Higher Dimensions.New York:Marcel Dekker, 2003 ?Received May 8,2015;revised April 6,2016.This work was supported by NSFC(11271359,U1204618), Science and Technology Research Projects of Henan Provincial Education Department(14B110015,14B110016), Youth Fund Projects of Zhoukou Normal University(zknuB3201608). ?Corresponding author:Hao LIU.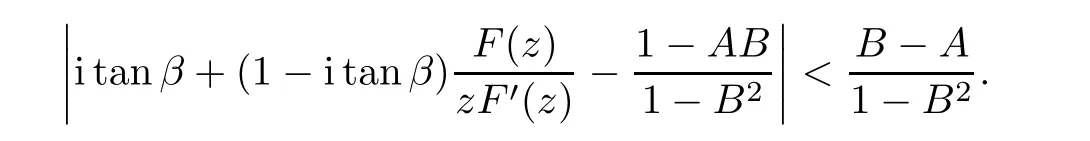

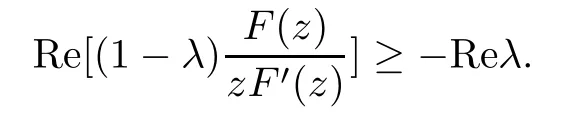
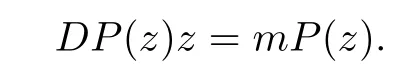
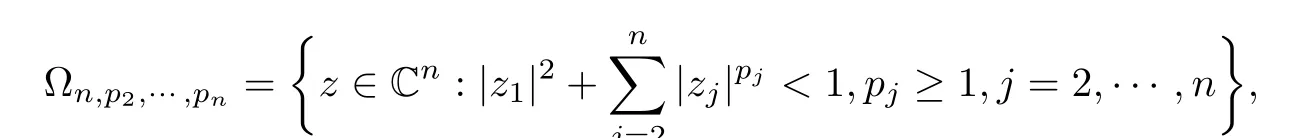
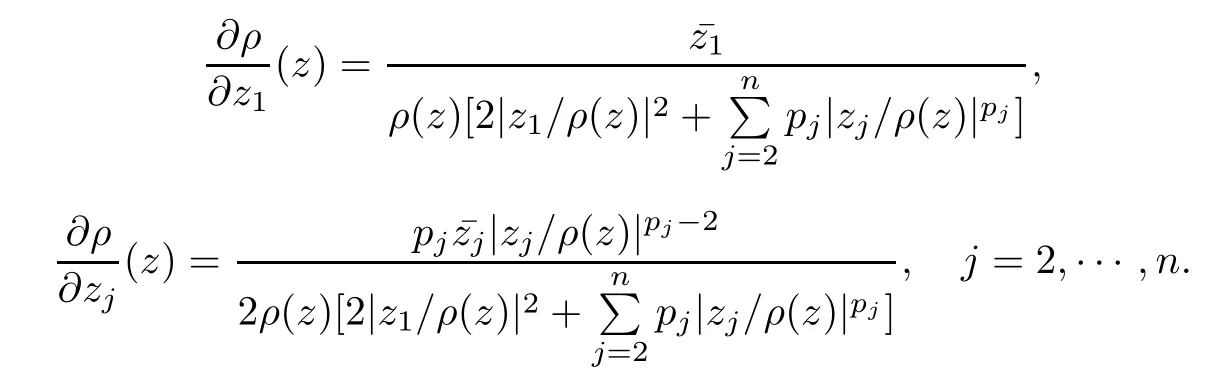
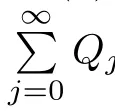

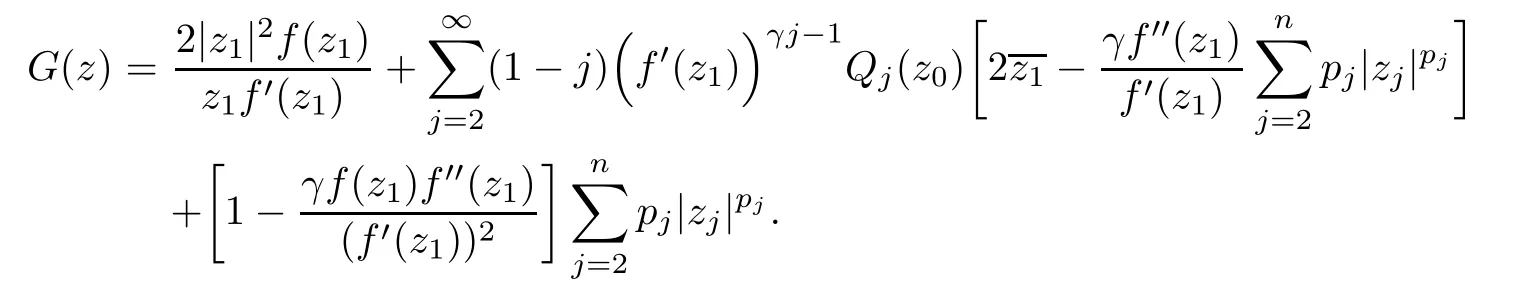

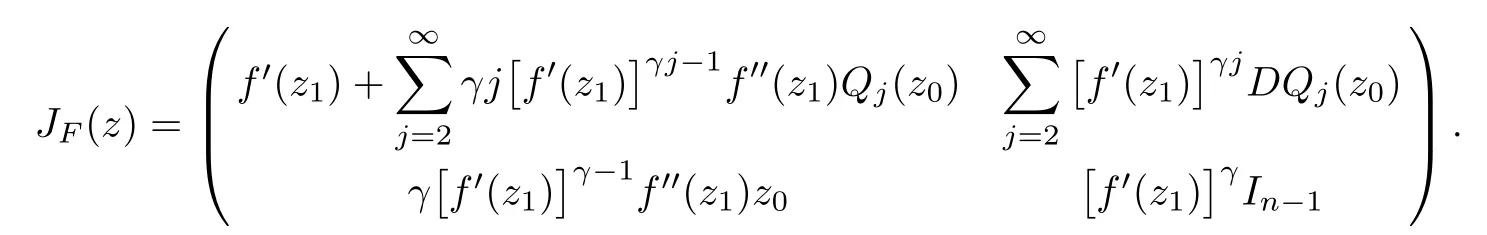

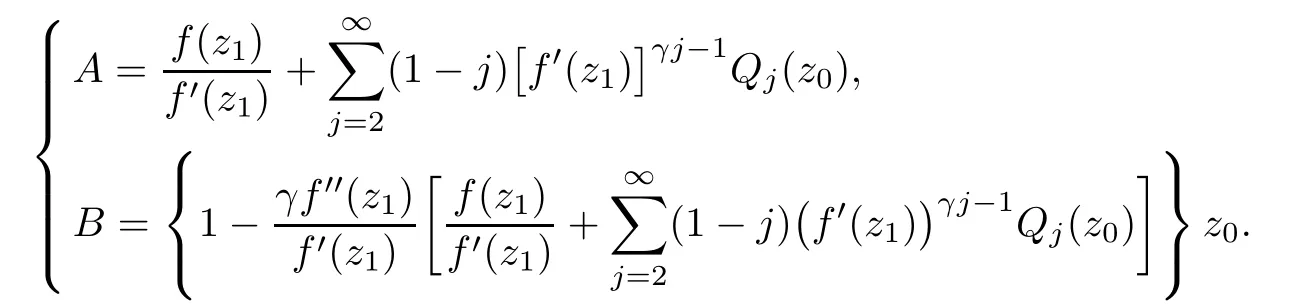
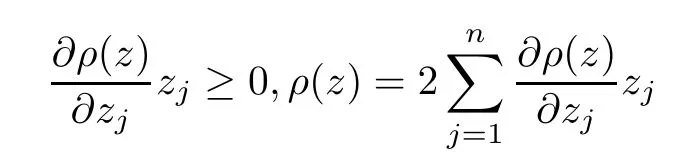
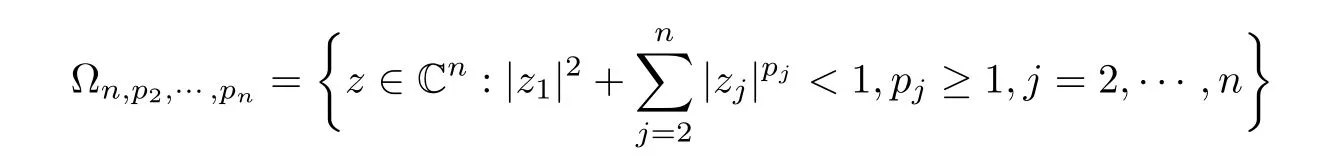

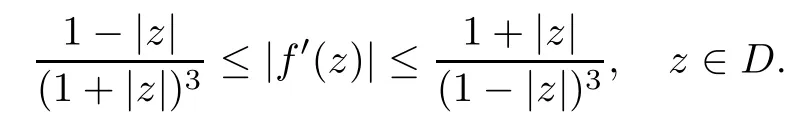
2 The Invariance of S??(β,A,B)
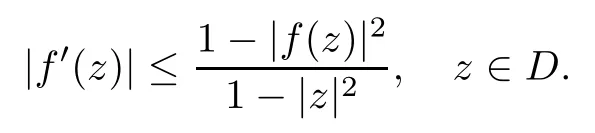
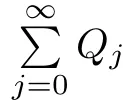

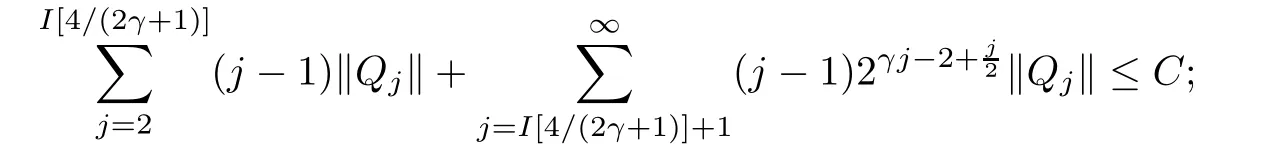
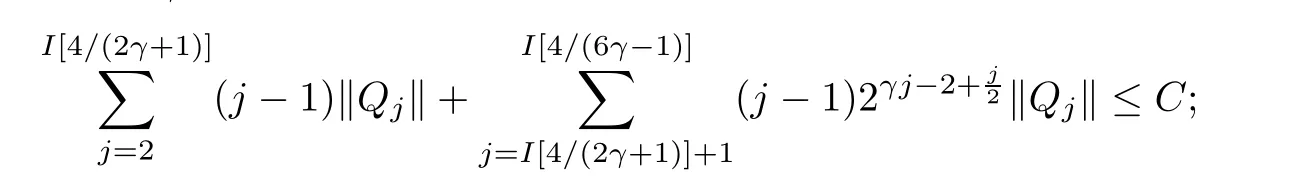

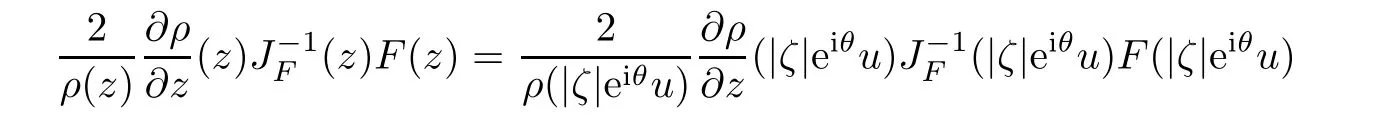
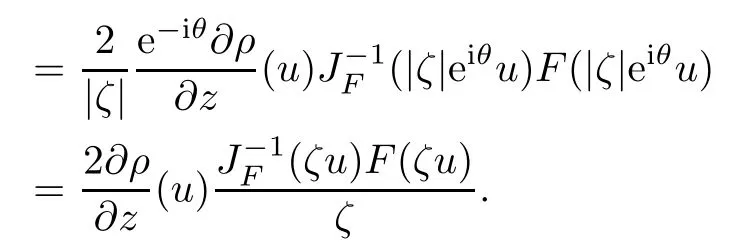
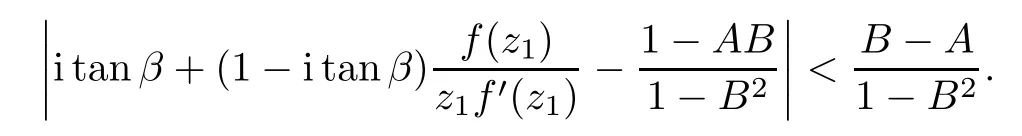
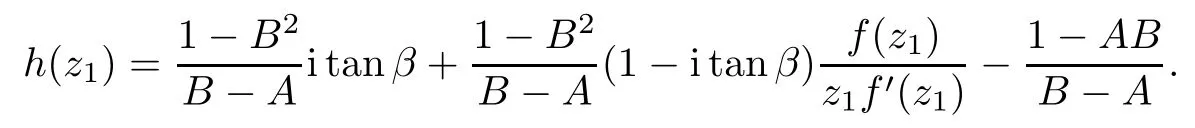
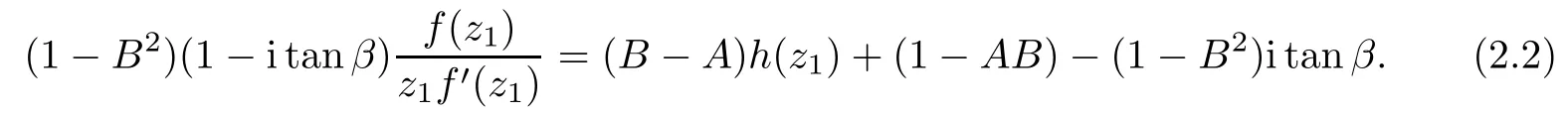


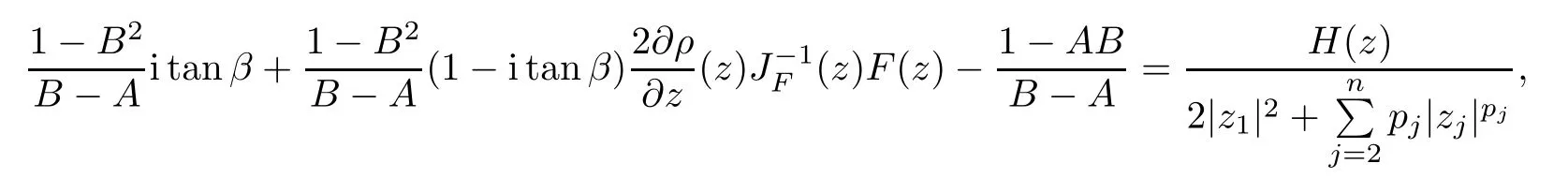





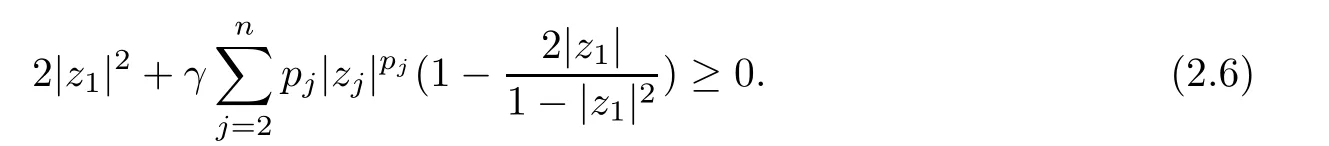
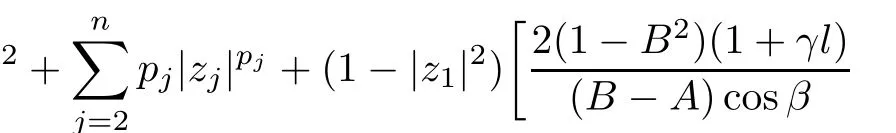
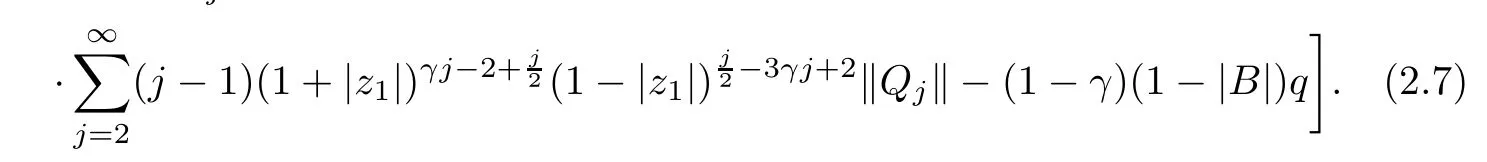
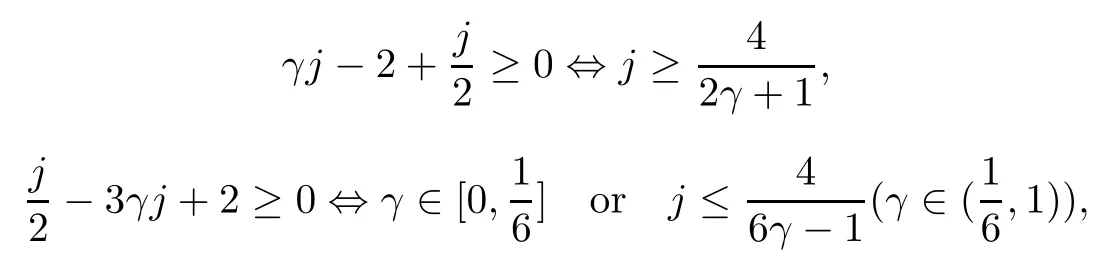
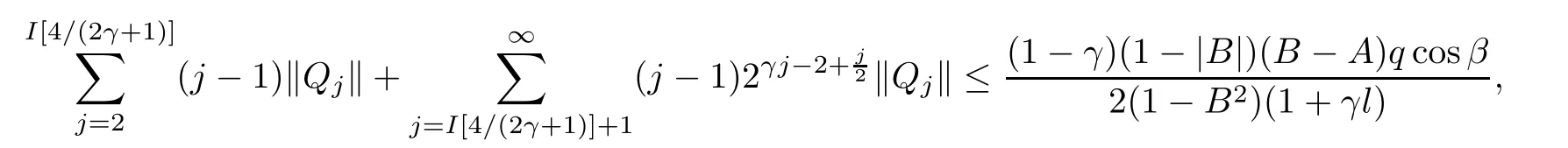
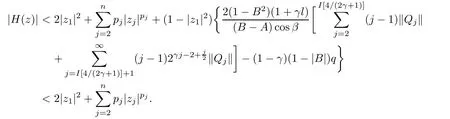
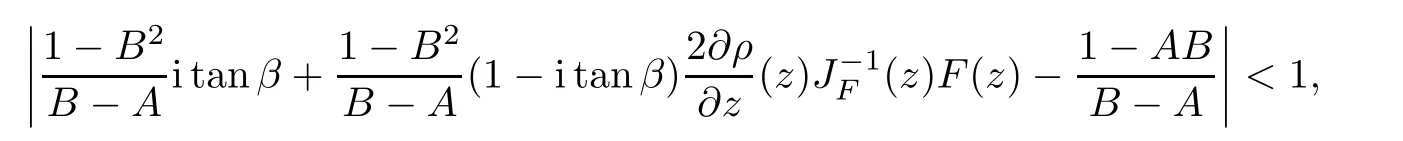
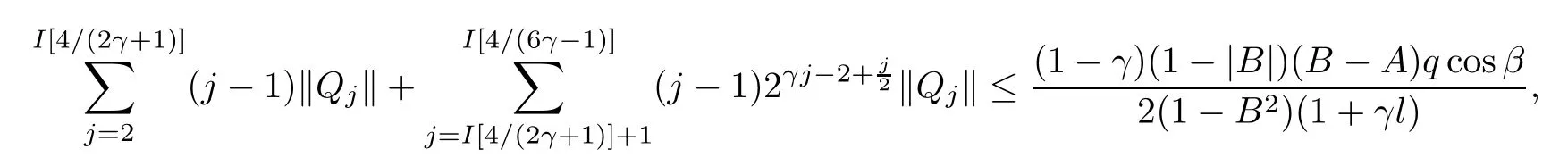

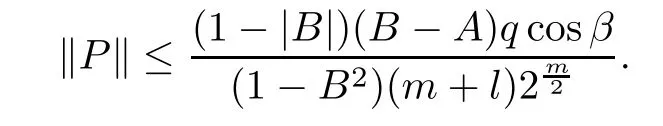
3 The Invariance of Almost Starlike Mappings of Complex Order λ
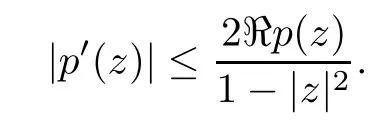



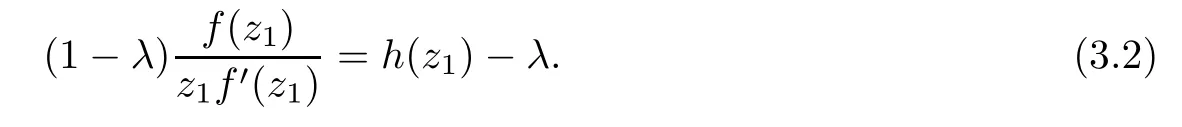

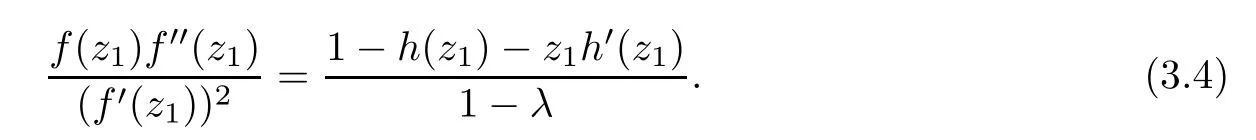
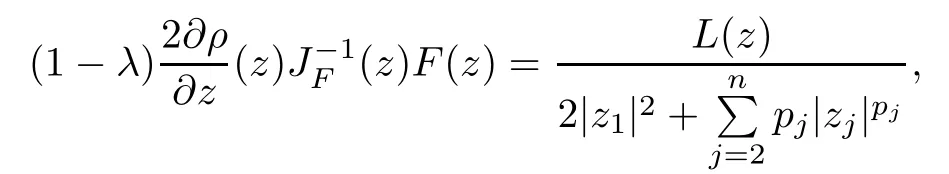

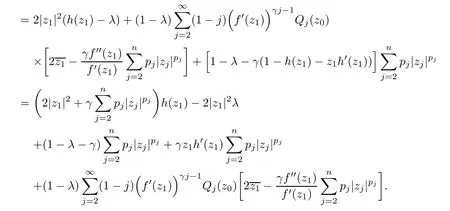
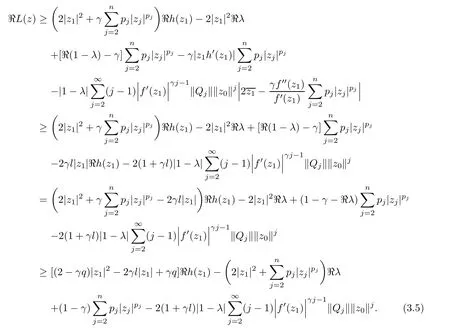
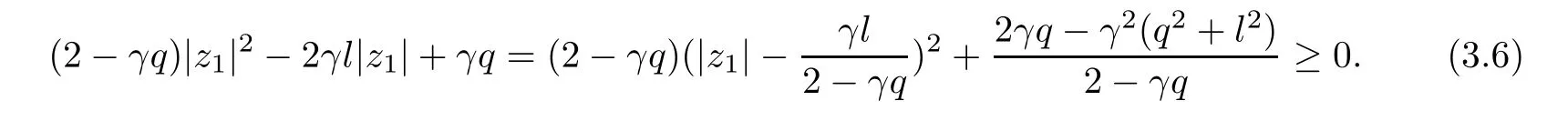
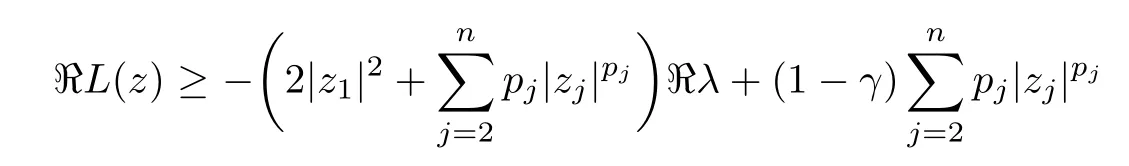

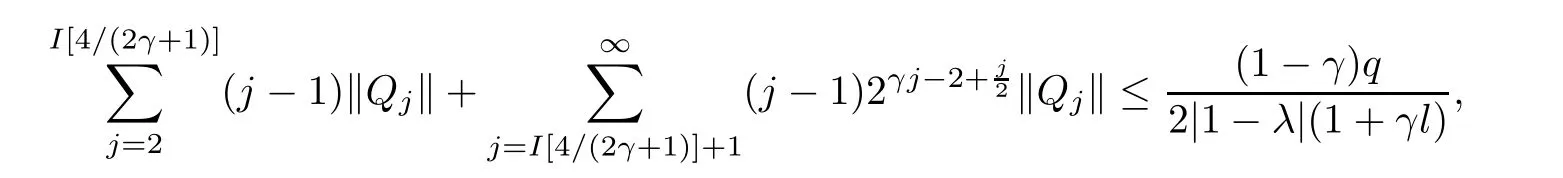


 Acta Mathematica Scientia(English Series)2016年6期
Acta Mathematica Scientia(English Series)2016年6期
