MULTIPLICITY RESULTS FOR A NONLINEAR ELLIPTIC PROBLEM INVOLVING THE FRACTIONAL LAPLACIAN?
Yongqiang XU(許勇強)
Department of Mechanical and Electrical Engineering,Xiamen University,Xiamen 361005,China; School of Mathematics and Statistics,Minnan Normal University,Zhangzhou 363000,China
Zhong TAN(譚忠)
School of Mathematical Sciences,Xiamen University,Xiamen 361005,China
Daoheng SUN(孫道恒)
Department of Mechanical and Electrical Engineering,Xiamen University,Xiamen 361005,China
MULTIPLICITY RESULTS FOR A NONLINEAR ELLIPTIC PROBLEM INVOLVING THE FRACTIONAL LAPLACIAN?
Yongqiang XU(許勇強)
Department of Mechanical and Electrical Engineering,Xiamen University,Xiamen 361005,China; School of Mathematics and Statistics,Minnan Normal University,Zhangzhou 363000,China
E-mail:yqx458@126.com
Zhong TAN(譚忠)
School of Mathematical Sciences,Xiamen University,Xiamen 361005,China
E-mail:ztan85@163.com
Daoheng SUN(孫道恒)
Department of Mechanical and Electrical Engineering,Xiamen University,Xiamen 361005,China
E-mail:sundh@xmu.edu.cn
In this paper,we consider a class of superlinear elliptic problems involving fractional Laplacian(??)s/2u=λf(u)in a bounded smooth domain with zero Dirichlet boundary condition.We use the method on harmonic extension to study the dependence of the number of sign-changing solutions on the parameter λ.
fractional Laplacian;existence;asymptotic;Sobolev trace inequality
2010 MR Subject Classifcation35J99;45E10;45G05
1 Introduction
Problems of the type

for diferent kind of nonlinearities f,were the main subject of investigation in past decades.See for example the list[2,4,5,10,14,16,17].Specially,in 1878,Rabinowitz[14]gave multiplicity results of(1.1)for any positive parameter λ as n=1.But he found that the number of solutions of(1.1)is independent on λ.Under some conditions on f,Costa and Wang[5]proved that the number of signed and sign-changing solutions is dependent on the parameter λ as n≥1.
Recently,fractional Laplacians attracted much interest in nonlinear analysis.Cafarelli et al.[7,8]studied a free boundary problem.Since the work of Cafarelli and Silvestre[9],whointroduced the s-harmonic extension to defne the fractional Laplacian operator,several results of version of the classical elliptic problems were obtained,one can see[3,6]and their references.
In this paper,we consider the nonlinear elliptic problem involving the fractional Laplacian power of the Dirichlet Laplacian

where ??Rn(n≥2)is a bounded domain with smooth boundary??,λ is a positive parameter, s∈(0,2),(??)s/2stands for the fractional Laplacian,and f:R→R satisfes:
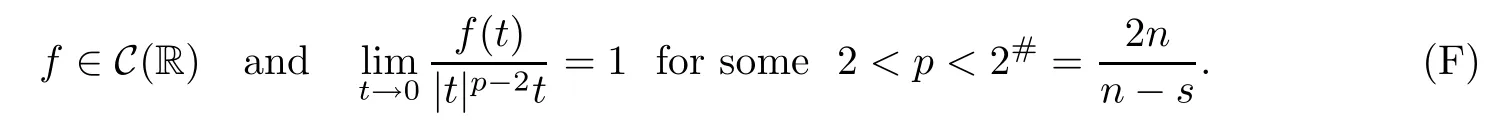
For the defnition of fractional Laplacian operator we follow some idea of[3].In particular, we defne the eigenvalues ρkof(??)s/2as the power s/2 of the eigenvalues λkof(??),i.e., ρk=λs/2kboth with zero Dirichlet boundary data.
Let N(λ)be the number of sign-changing solutions of(Pλ).Our main result is the following theorem.
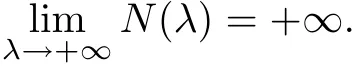
2 Preliminaries
Denote the half cylinder with base on a bounded smooth domain ? by
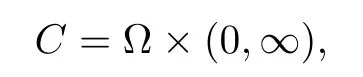
and its lateral boundary by
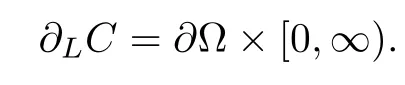
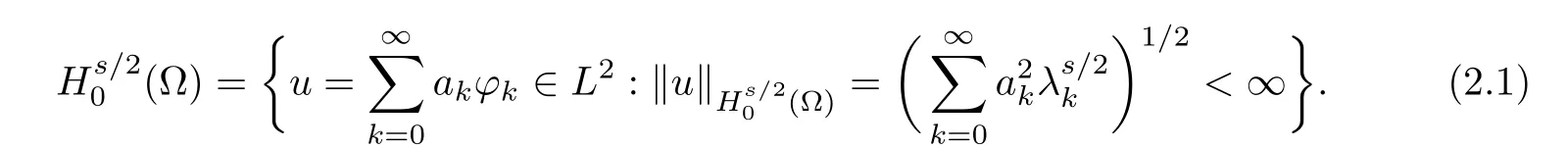
Denote H?s/2(?)the dual space of Hs/20(?).(??)s/2is given by
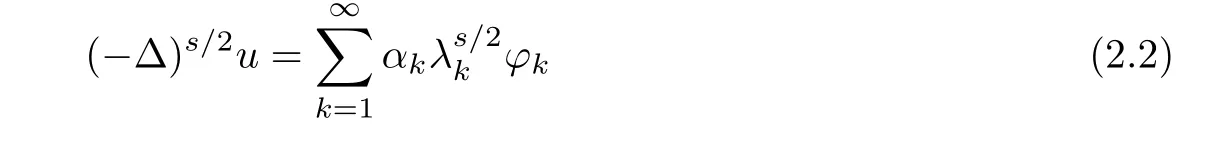
Associated to problem(Pλ),the corresponding energy functional I1:Hs/20(?)→ R is defned as follows:

Defnition 2.1We say that u∈Hs/20(?)is a weak solution of(Pλ)if
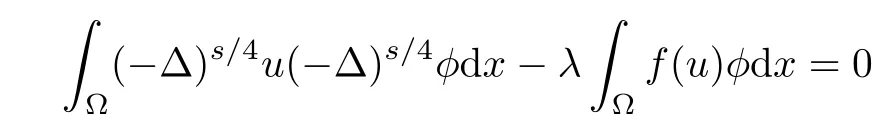
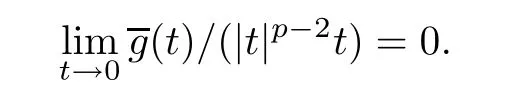
So if δ>0 small enough,there exists Cδ>0 such that
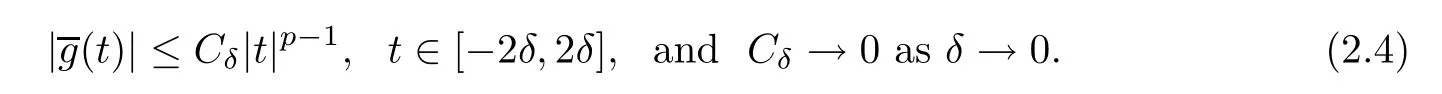
Let δ>0 be small enough such that

and(2.4)is satisfed.Let βδbe a C∞function satisfying that βδ=1 if|t|≤δ,βδ=0 if |t|≥2δ,and 0≤βδ≤1,for any t∈R.Defne

and consider the following equation

Combining(Pλ)with(2.6),through direct calculation,we have the following lemma.
Lemma 2.1If w is a solution of(Qδ,λ)and

then u(x)=λ?1/(p?2)w(x),x∈? is a solution of Pλ.
To treat the nonlocal Qδ,λ,we will study a corresponding extension problem in one more dimension,which allows us to investigate Qδ,λby studying a local problem via classical nonlinear variational methods.
For any regular function u,the fractional Laplacian(??)s/2acting on u is defned by
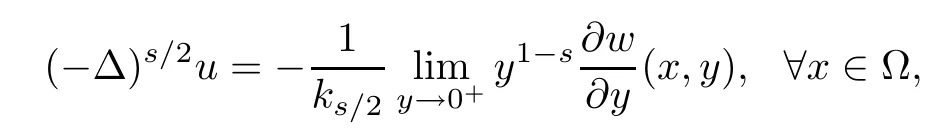
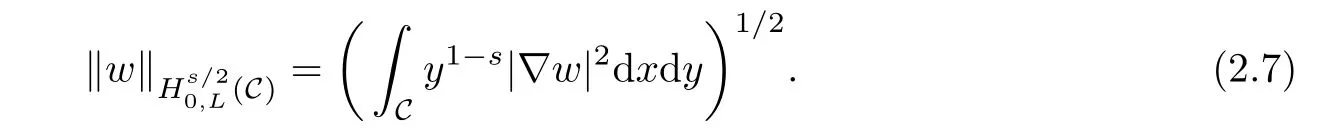
In fact the extension technique is developed originally for the fractional Laplacian defned in the whole space[9],and the corresponding functional spaces are well defned on the homogeneous fractional Sobolev spaceand the weighted Sobolev spaceIf φ is smooth enough,it can be computed by the following singular integral:where P.V.is the principal value and cn,s/2is a normalization constant.And it is obtained, from[9],that formula(2.8)for the fractional Laplacian in the whole space equivalent to that obtained from Fourier transform(i.e.,the fractional Laplacian(??)s/2of a function φ∈S is defned by

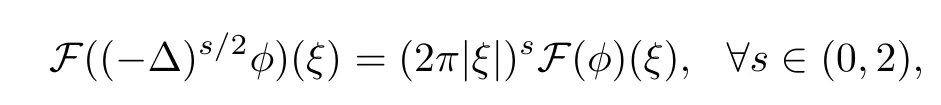
where S denotes the Schwartz space of rapidly decreasing C∞function in Rn,F is the Fourier transform).
With this extension,we can reformulate our problem(Qδ,λ)as

Defnition 2.2We say that u∈Hs/20(?)is an energy solution of problem(Qδ,λ)if u=tr?w,wheresatisfes
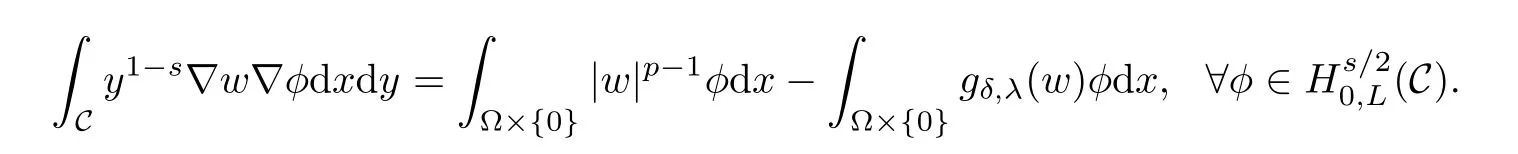
The corresponding energy functional is defned by
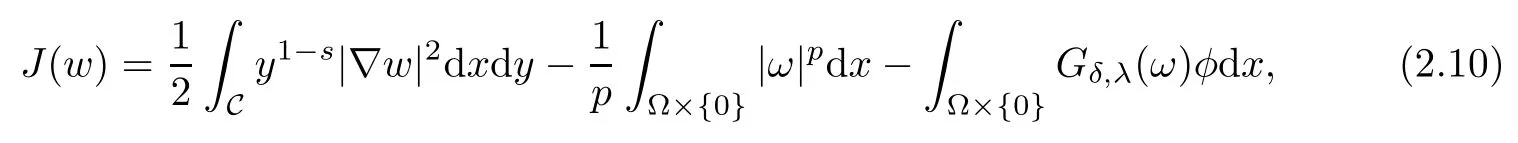
In the following,we collect some results of the space
Lemma 2.2(see[3]) Let n≥s and 2#=2n
n?s.Then there exists a constant C,depending only n,such that,for all ω∈Hs/20,L(C),
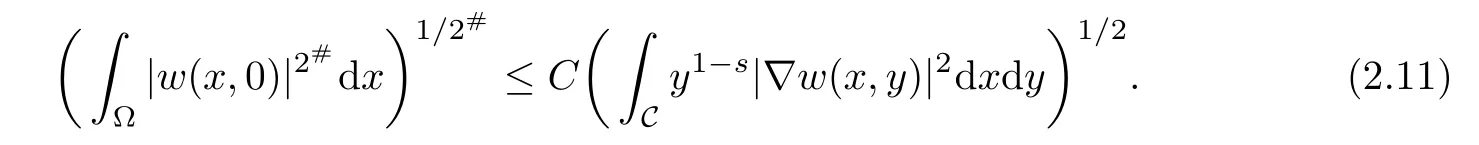
By H¨older’s inequality,since ? is bounded,the above lemma leads to:
Lemma 2.3(see[3]) (i) Let 1≤ q≤ 2#for n≥ s.Then,we have that for all
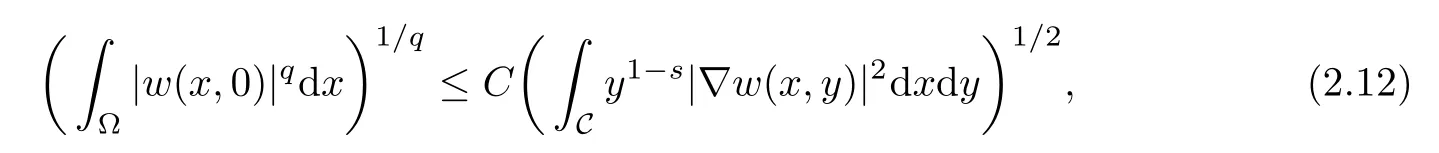
where C depends only on n,q and the measure of ?.
Lemma 2.4(see[3])
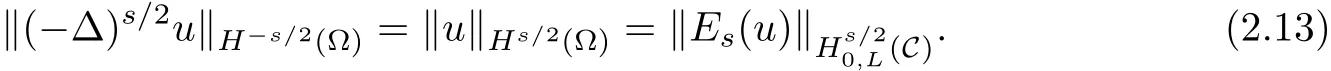
3 Proof of Theorem 1.1

and

The following lemma is an elliptic regularity result,which is crucial in our proof.That is, we deduce the regularity of bounded weak solutions to the nonlinear problem
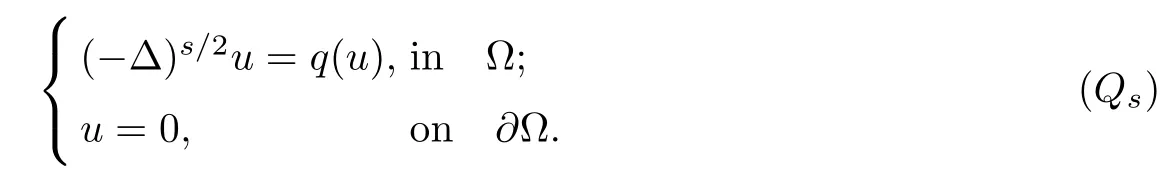
Lemma 3.1Assume n≥2.Let q∈C(R)andfor some constantis a weak solution of the nonlinear problem(Qs),then there exists C=C(p,L,n)>0 such that

ProofAs before,the precise meaning for(Qs)is that w∈Hs/20,L(C),w(·,0)=u,and w is a weak solution of
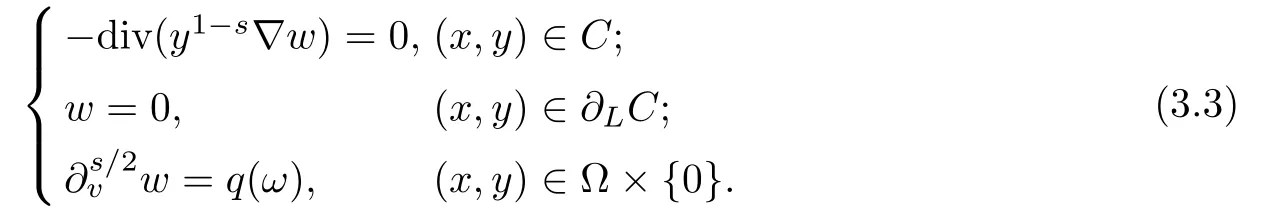
Denote
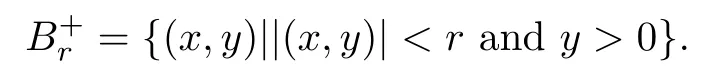
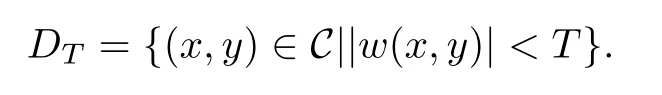
By direct computation,we see
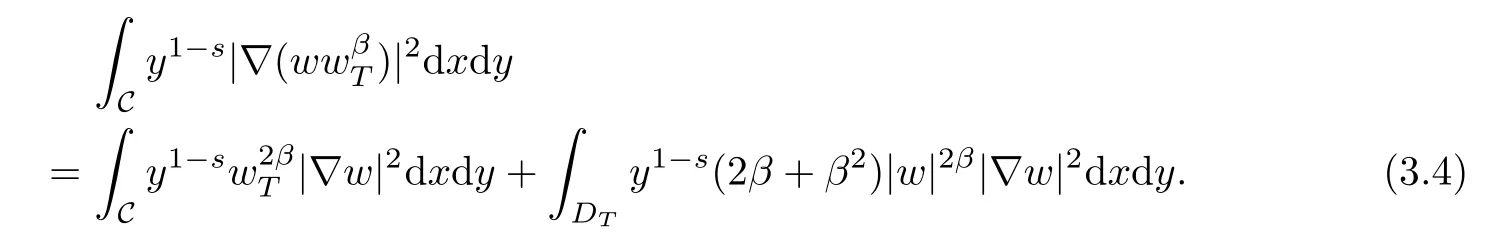
Multiplying(3.3)by ?β,Tand integrating by parts,we obtain
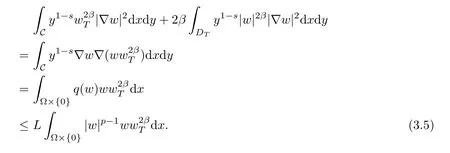
Combining(3.4)and(3.5),we have
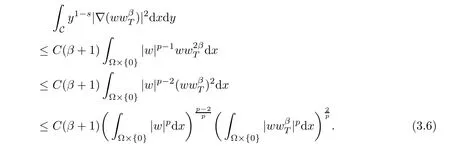
On the other hand,
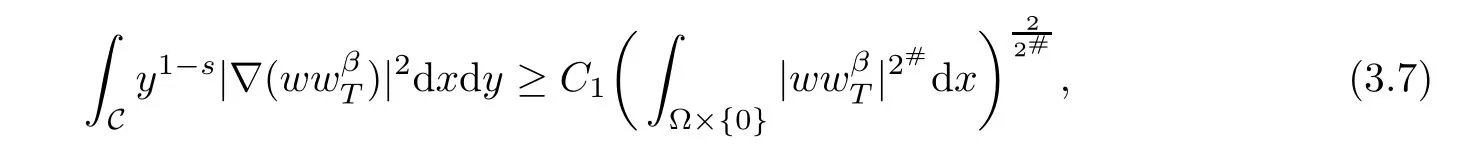
where C1dependent on n and q,and q>p.
From(3.6)–(3.7),we have
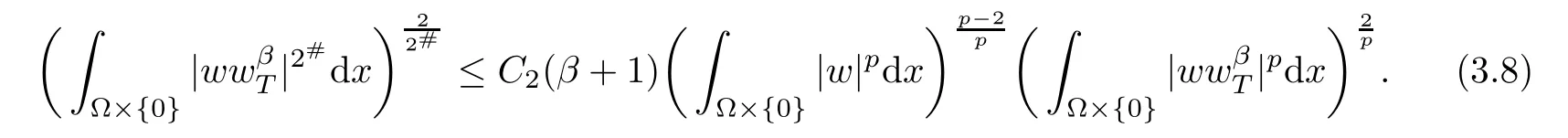
Let T→∞,we get
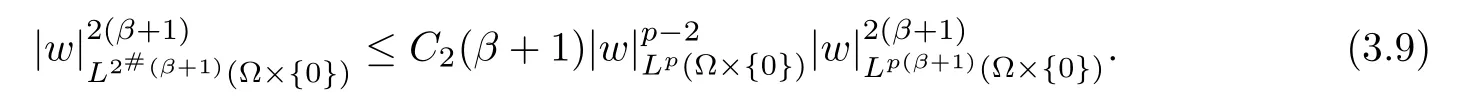
So,we have
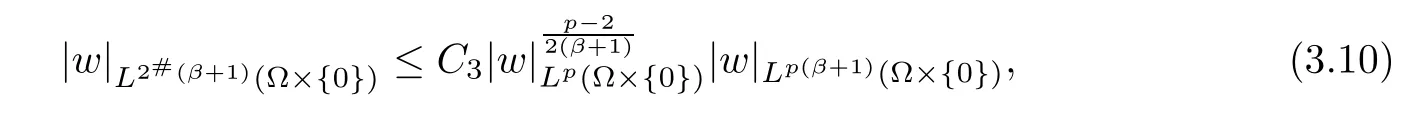
where
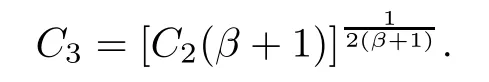
Let l=p(β+1),then
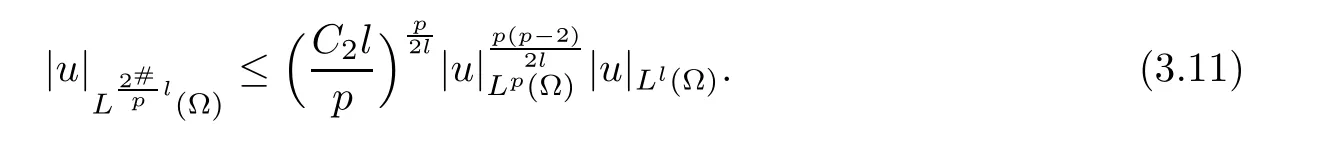
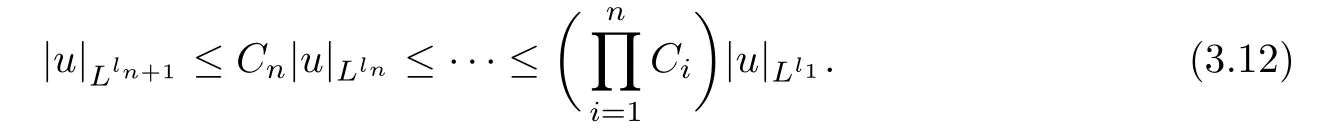
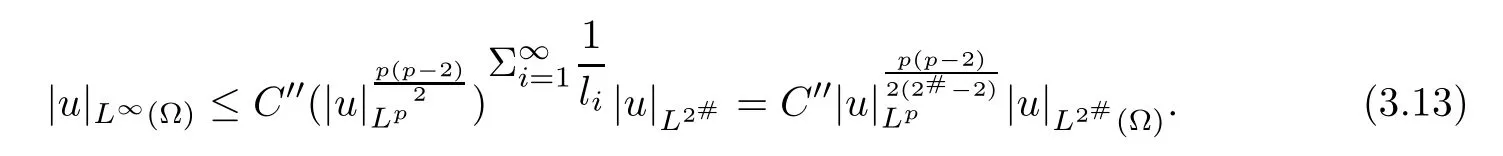
By Sobolev inequality,we have
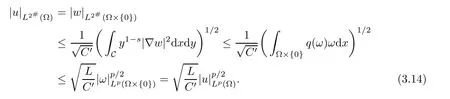

So,we fnish the proof of Lemma 3.1.
Defne

and
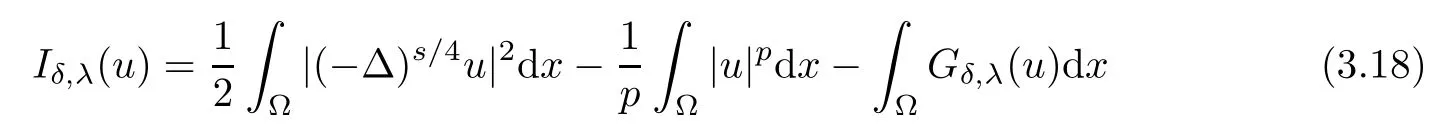
By(2.5)and(3.1),we have
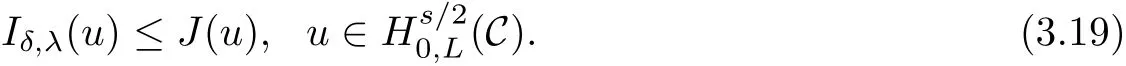
Lemma 3.2Under assumption(F),the functionals I and Iδ,λsatisfy(PS)cconditions.
ProofWe just prove the case that Iδ,λsatisfes(PS)cconditions.The other case can be obtained similarly.Assume that there exists a(PS)csequence{uk}?Hs/20(?),i.e.,
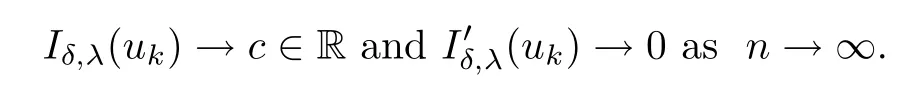
By(F),we get
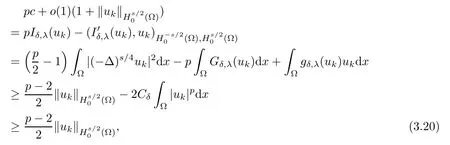
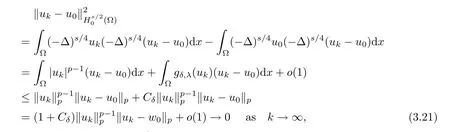
which implies that wk→w0in Hs/20(?),as k→∞.Using the same method,we can prove that I also satisfes(PS)ccondition.
Proof of Theorem 1.1In order to employ the method from[12],we defne,on E(=
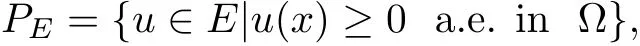
which is a closed convex cone.From[1](Theorem 7.38),we know that the Banach spaceis densely embedded inand
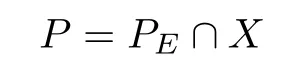
is a closed convex cone in X.Furthermore,P=P?∪P under the topology of X,i.e.,there exist interior points in P.So,as in[12],we may defne a partial order relation in X:u,v∈X,u>v?u?v∈P{0};u?v?u?v∈P?.We also defne W=P∪(?P).
Defne
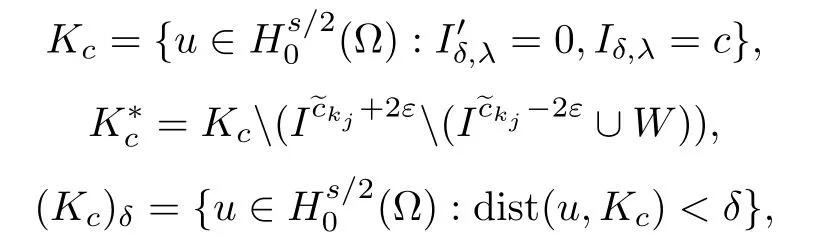
we obtain the similar deformation lemma.
Lemma 3.3Fix c≥0 and ε∈(0,14].Then,there exists a homeomorphism map η:such that
ProofFirst,due to(PS)ccondition,we can choose a constant ε>0 such that

Let
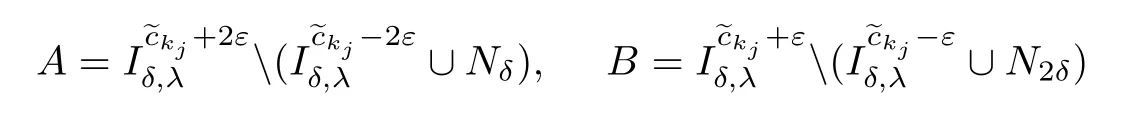
and
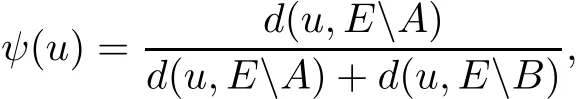
where

Then ψ(u)is locally Lipschitz on E,consider
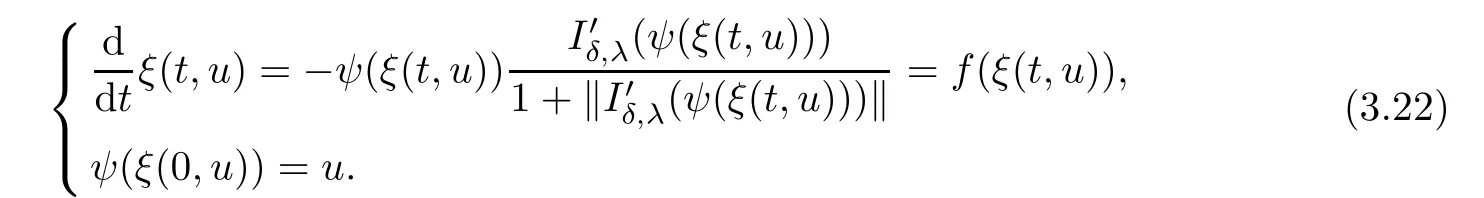
Since kf(ξ(t,u))k≤1 for all ξ(t,u)the Cauchy problem(3.22)has a unique solution ξ(t,u)continuous on R×E.Follow the argument as in[13],we can obtain that there exist T>0 such that η(u)=ξ(T,u)satisfes the conclusion.
Denote by 0<λ1<λ2≤λ3≤···all the eigenvalues of??in ? with zero Dirichlet boundary condition and by e1,e2,e3,···the corresponding eigenfunctions,with the explicit meaning that each λiis counted as many times as its multiplicity.
Denote
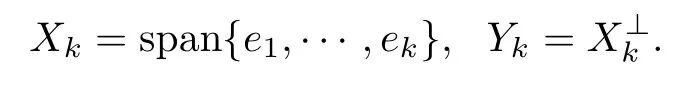
Let ri>0 be such that ri+1>rifor i=1,2,···,ri→∞(i→∞)and
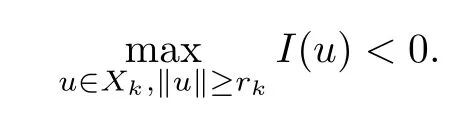
Let

and?Bkbe the boundary of Bkin Xk.Defne a sequence{Λk}of functions inductively as
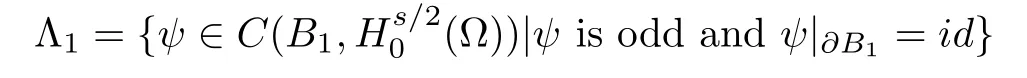
and for k=2,3,···
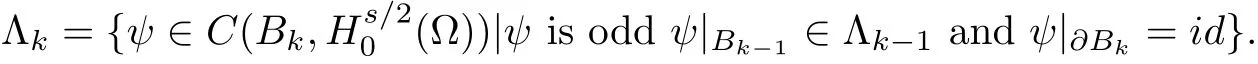
Defne,for k=1,2,···,
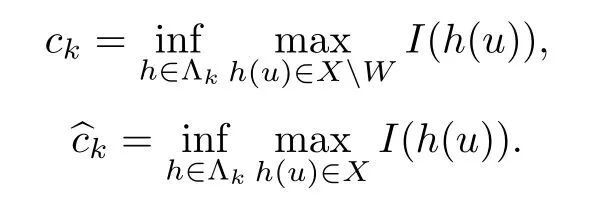
Using the similar method as(Proposition 5.2,[11]),we can obtain that when n≥ 2, there exist non-positive constants C and D such thatfor k∈N,where γ=(s/n)p(p?2)?1.
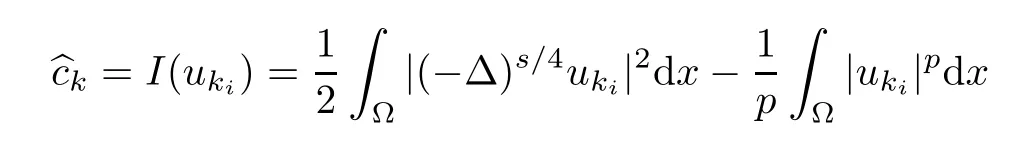
and
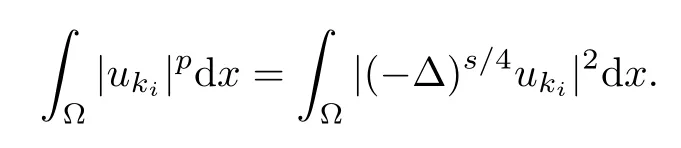
Thus,
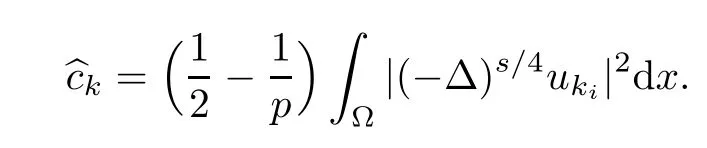
So,
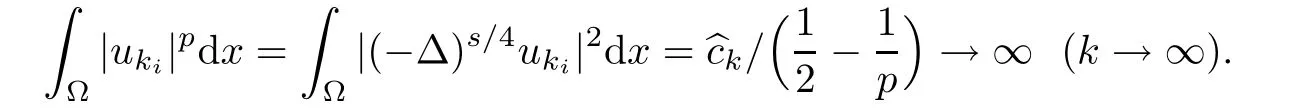
On the other hand,using the similar method from[15],we have
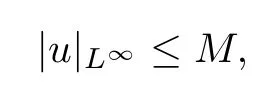
where M is a constant dependent on p,n and ?,which is a contradiction.
Thus for n≥2,there exists a sequence{kj}?N such that
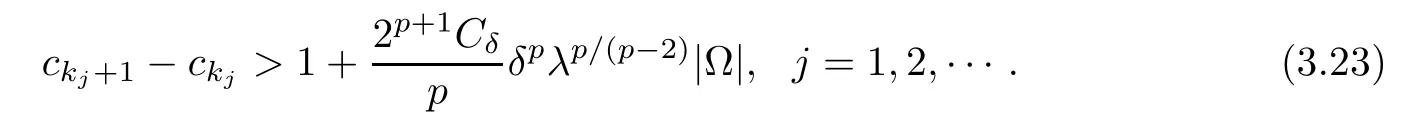
For j=1,2,···,defne

By(3.23),it is easy to deduce that
Claim 1


and by(3.19),

Claim 2is a critical value of Iδ,λ.

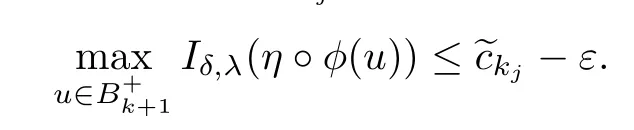
It contradicts to the defnition of
If ujis a critical point of Iδ,λandthen
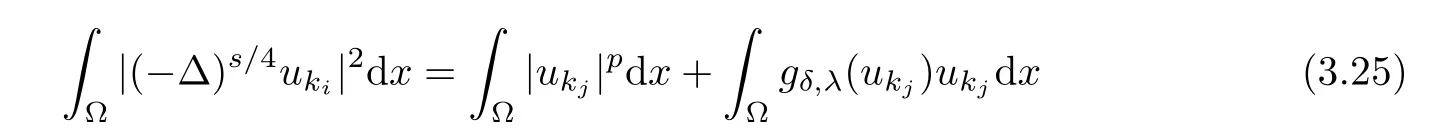
and

Combining(3.25)–(3.26),(2.5),(3.1)and Claim 1,we have

Since
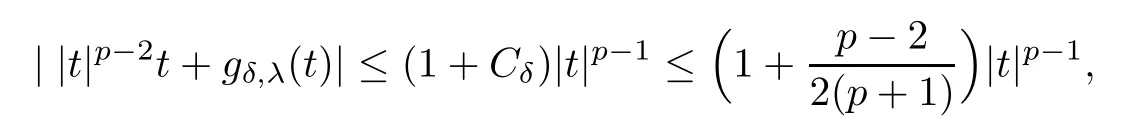
and dkjis independent of δ and λ,by Lemma 3.1,we know that for any j∈N,there is λj>0 such that for any λ≥λj,

Then by Lemma 2.1,and using the similar argument as[12],we can prove that when λ≥λjandis a sign-changing solution of(Pλ).Thus
[1]Adams R A.Sobolev Spaces.New York:Academic Press,1975
[2]Bahri A,Lions P L.Solutions of superlinear elliptic equations and their Morse indices.Comm Pure Appl Math,1992,45:1205–1215
[3]Barrios B,Colorado E,de Pablo A,S′anchez U.On some critical problems for the fractinal Laplacian operator.J Difer Equ,2012,252:6133–6162
[4]Cao D M.Multiple positive solutions of inhomogeneous semilinear elliptic equations unbounded damain in R2.Acta Math Sci,1994,14(2):297–312
[5]Costa D G.Multiplicity results for a class of superlinear elliptic problems.Amer Math Soc,1993,48: 137–151
[6]Cabr′e X,Tan J.Positive solutions of nonlinear problems involving the square root of the Laplacian.Adv Math,2010,224:2052–2093
[7]Cafarelli L,Roquejofre J M,Sire Y.Variational problems for free boundaries for the fractional Laplacian. J Eur Math Soc,2010,12:1151–1179
[8]Cafarelli L,Salsa S,Silvestre L.Regularity estimates for the fractional Laplacian.Invent Math,2008,171: 425–461
[9]Cafarelli L,Silvestre L.An extension problem related to the fractional Laplacian.Commun Part Difer Equ,2007,32:1245–1260
[10]Deng Y B,Li Y,Zhao X J.Multiple solutions for an inhomogeneous semilinear elliptic equation in Rn. Acta Math Sci,2003,23(1):1–15
[11]Ekeland I,Choussoub N.Selected new aspects of the calculus of variations in the large.Bull Amer Math Soc,2002,39:207–265
[12]Li S J,Wang Z Q.Ljusternik-Sohnirelman theorey in partially order Hilber space.Trans Amer Math Soc, 2002,354:3207–3227
[13]Liu Z L,Wang Z-Q.Sign-changing solutions of nonlinear elliptic equations.Front Math China,2008,3: 1–18
[14]Rabinowitz P H.Some minimax theorems and applications to nonlinear PDE//Nonlinear Analysis.Acad Press,1978:161–177
[15]Tan J.Positive solutions for non local elliptic problems.Disc Cont Dyn Syst,2013,33:837–859
[16]Wang Z-Q.On a superlinear elliptic equation.Anal Nonl,1991,8:43–58
[17]Wang Z-Q.Multiplicity results for a class of superlinear elliptic problems.Amer Math Soc,2004,133: 787–794
?Received April 4,2015;revised May 12,2016.This research was supported by China Postdoctoral Science Foundation Funded Project(2016M592088)and National Natural Science Foundation of China-NSAF (11271305).
 Acta Mathematica Scientia(English Series)2016年6期
Acta Mathematica Scientia(English Series)2016年6期
- Acta Mathematica Scientia(English Series)的其它文章
- NEW LOWER BOUNDS FOR LEE DISCREPANCY ON TWO AND THREE MIXED LEVELS FACTORIALS?
- THREE SOLUTIONS FOR A FRACTIONAL ELLIPTIC PROBLEMS WITH CRITICAL AND SUPERCRITICAL GROWTH?
- SHARP ESTIMATES OF ALL HOMOGENEOUS EXPANSIONS FOR A SUBCLASS OF QUASI-CONVEX MAPPINGS OF TYPE B AND ORDER α IN SEVERAL COMPLEX VARIABLES?
- EXISTENCE AND UNIQUENESS OF NON-TRIVIAL SOLUTION OF PARABOLIC p-LAPLACIAN-LIKE DIFFERENTIAL EQUATION WITH MIXED BOUNDARIES?
- PROPERTIES OF THE MODIFIED ROPER-SUFFRIDGE EXTENSION OPERATORS ON REINHARDT DOMAINS?
- ON DOUBLY WARPED PRODUCT OF COMPLEX FINSLER MANIFOLDS?
