Momentum-space polarization fields in two-dimensional photonic-crystal slabs: Physics and applications

Wen-Zhe Liu(劉文哲) Lei Shi(石磊) Che-Ting Chan(陳子亭) and Jian Zi(資劍)

1Department of Physics,The Hong Kong University of Science and Technology,Hong Kong 999077,China

2State Key Laboratory of Surface Physics,Key Laboratory of Micro-and Nano-Photonic Structures(Ministry of Education),and Department of Physics,Fudan University,Shanghai 200433,China

3Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China

Keywords: photonic crystal,polarization field,polarization singularity

1. Introduction

As a new kind of optical media,photonic crystals(PhCs)are periodic photonic structures characterized by complicated photonic band structures and even photonic band-gaps,[1,2]offering unprecedented opportunities to manipulate the flow of light and novel applications in photonics and optoelectronics as well. In particular, two-dimensional (2D) PhC slabs have drawn considerable attention due to the fact that they can support non-radiative guided modes with great promise for miniaturized integrated photonic circuits.[3]

As a representative example of photonic systems with open boundaries, 2D PhC slabs support also guided resonant modes inside the light cone.[4–6]These guided resonant modes are leaky since they can couple with far-field modes in free space. Like non-radiative guided modes,radiative guided resonances also display similar photonic band structures in reciprocal or momentum space due to the introduced periodicity. Radiative photonic bands can be tailored by changing the structural and material parameters of 2D PhC slabs,giving rise to interesting scattering and radiation properties such as anomalous transmission and directive radiation.[7,8]

Recently,polarization fields in momentum space,defined on radiative photonic bands, were introduced[9]in discussing the optical properties of guided resonant modes, particularly on optical bound states in the continuum(BICs)found in 2D PhC slabs and other periodic photonic structures with open boundaries.[9–12]The introduction of momentum-space polarization fields could not only deepen our understandings of periodic photonic structures with open boundaries but also shed new light on their applications. In this paper,we review recent progress in the study of momentum-space polarization fields and singularities in 2D PhC slabs, including the concept and the resulting physical implications in Section 2,evolutions under symmetry perturbations in Section 3, and potential applications in Section 4. Although we focus mainly on 2D PhC slabs, interesting work on other periodic photonic structures with open boundaries will be also discussed.

2. Momentum-space polarization fields on photonic bands

Light waves are inherently vectorial in nature.[13–15]As a result,polarization states,which describe the trajectories of oscillating electric field vectors, are one of the key characteristics of light,in addition to frequency,amplitude,and phase.

In general, polarization states are inhomogeneous. For a polarized monochromatic light beam, its space-varied polarization states on the transverse plane form a 2D polarization field. There may exist polarization singularities in this field such as vector singularity points (V-points, null-amplitude points around which polarization states are winding and tend to be linear),[16]circularly-polarized points(C-points,around which polarization states have winding major axes and tend to be circular),[17,18]and linearly-polarized lines (L-lines, near which polarization states tend to be linear), schematically shown in Fig.1. These polarization singularities are topologically non-trivial since they are stable under smooth deformations of polarizations fields. Thus,V-points and C-points can be described by a topological chargeqdetermined by winding the polarization orientations around them. V-points can be viewed as the result of collisions between C-points and Llines, implying that V-points are usually located on L-lines.Morphologies and topological behaviors of polarization singularities have been extensively studied since discovered by Nye and Berry,[17,19]and become an important part of the emerging field of singular optics.[20–22]

Fig. 1. Schematic of a polarization field with polarization singularities such as V-points, C-points, and L-lines. For any electromagnetic field,coordinate-dependent polarization states can be defined and mapped onto an arbitrary 2D parametric space,forming a 2D polarization field.

In recent years, many interesting studies on polarization fields in real space have been conducted.[21,23–26]Indeed,polarization fields could be also defined in other parametric spaces.[27–35]For example, polarization ellipses at different parametric coordinates can be mapped onto a 2D parametric plane to construct a polarization field.[36]Such polarization fields in parametric spaces may offer new perspectives, connecting mathematical vectorial structures to physical properties. Polarization fields discussed in this paper are defined in momentum space of periodic photonic structures with open boundaries. By inspecting these momentum-space polarization fields,we could deepen our understanding of the underlying physics in such systems.

We first discuss the definition of momentum-space polarization fields on photonic bands. We consider a 2D PhC slab which supports Bloch modes with well-defined in-plane wavevectors (k‖). These Bloch modes are characterized by photonic band structures in momentum space, i.e., the Brillouin zone.[37–39]Note that modes with wavevectorsk‖+Gare equivalent, whereGis the reciprocal lattice vector. Suppose that the PhC slab lies in thex–yplane and the surface normal is along thezdirection. Those Bloch modes with frequencies and in-plane wavevectors outside the light cone of free space are non-radiative guided waves. However, Bloch modes inside the light cone are radiative since they can couple with far-field modes of free space. Therefore,they are guided resonant modes in nature.[40,41]For each resonant mode,there exist series of radiation channels with wavevectors satisfyingk0=k‖+kz+G,wherek0is the free-space wavevector with an out-of-plane componentkz. Once excited,a resonant mode can radiate through these radiation channels. The radiating polarization states of the outgoing plane waves, described by a Jones vector composed of electric field components(Ep,Es)or(Ex,Ey)on thex–ybasis,[42]can be defined as the polarization states atk‖+G. Focusing on the modes on one specific photonic band, the corresponding polarization states can be mapped onto thek‖space such that a 2D polarization field is constructed in momentum space,[9,43,44]as shown in Fig.2(a).Within the constructed field,polarization singularities may appear. The topological chargeqof a polarization singularity in momentum space is defined as the winding number of the polarization vector(major axis for elliptic polarization),

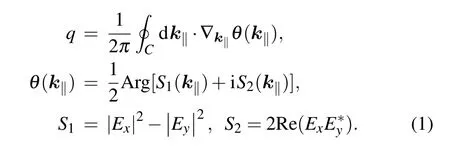
Here,S1andS2are the first and second Stokes parameters of a momentum-space polarization state. Unlike photonic band structures, this field is not periodic since one radiation channel with a free-space wavevectork0=k‖+kz+Gis obviously not equivalent to another diffracted one withk′0=k‖+k′z+G′.

Momentum-space polarization fields defined on photonic bands display complicated patterns including polarization singularities such as V-points, C-points, and L-lines, depending strongly on the structural and material parameters of the 2D PhC slabs. These fields could offer new perspectives on getting deep insight into the interactions between 2D PhC slabs and light, and novel applications as well, as schematically shown in Figs. 2(b)–2(d). For instance, optical properties such as the radiation and scattering of a 2D PhC slab can be tailored by modifying its momentum-space polarization fields since both thek‖-dependent radiation behaviors and angle-dependent scattering properties depend strongly on these fields. By changing the symmetry of a 2D PhC slab,the resulting momentum-space polarization fields will alter accordingly, leading to desired angle-dependent radiations, and phase and polarization modulations. Different distributions of polarization states in momentum space can be exploited to realize novel optical phenomena such as suppressing radiation,beam shifting,and wave-front reshaping.

Fig.2. (a)Schematic of a polarization field defined on a photonic band of a 2D PhC slab in momentum space. Polarization singularities may appear in such a field. (b) Momentum-space polarization fields stem from the complicated interactions between a 2D PhC slab and free space, i.e., the radiation from the photonic system and the scattering by the system. (c) By tuning polarization fields, lifetime, phase, and polarization of light radiated from and scattered by the system can be modulated,leading to interesting phenomena as illustrated in(d).

3. Evolutions of momentum-space polarization fields

A crucial feature in momentum-space polarization fields is the existence of polarization singularities. Due to the topological nature, these singularities affect the polarization states in their vicinity significantly. Among all types of polarization singularities, V-points might be the most interesting ones. With zero intensities, radiations stemming from V-points should vanish. When all the radiation channels of a resonant mode get blocked by V-points, this mode would become non-radiative, namely, a BIC, found theoretically by Zhenet al.in 2014[9]and confirmed by others.[31,45]Four years later, Zhanget al.[43]carried out the first experimental observations of such V-points in momentum-space polarization fields. Home-built momentum-space imaging spectroscopy was used to measure the reflection spectra of aC4vsymmetric 2D plasmonic-crystal structure, shown in Fig. 3.Obviously, this photonic structure is characterized by photonic band structures represented by extinction spectra. With a temporal coupled-mode theory, the authors confirmed the existence of BICs, manifesting as the vanishing points in the extinction spectra. Five V-points or BICs with topological charges±1 can be clearly seen in the reconstructed momentum-space polarization field on the first TM-like photonic band from polarization-dependent measurements.One is located at the center of momentum space(Γpoint)and four on the mirror-symmetrical directions (Γ–X). As expected, resonant modes around V-points possess very high radiative quality factors (Qs), implying that V-points could have great potential for lasing and non-linear optical processes. Note that a V-point was also experimentally observed at theΓpoint in a 2D PhC slab.[46]

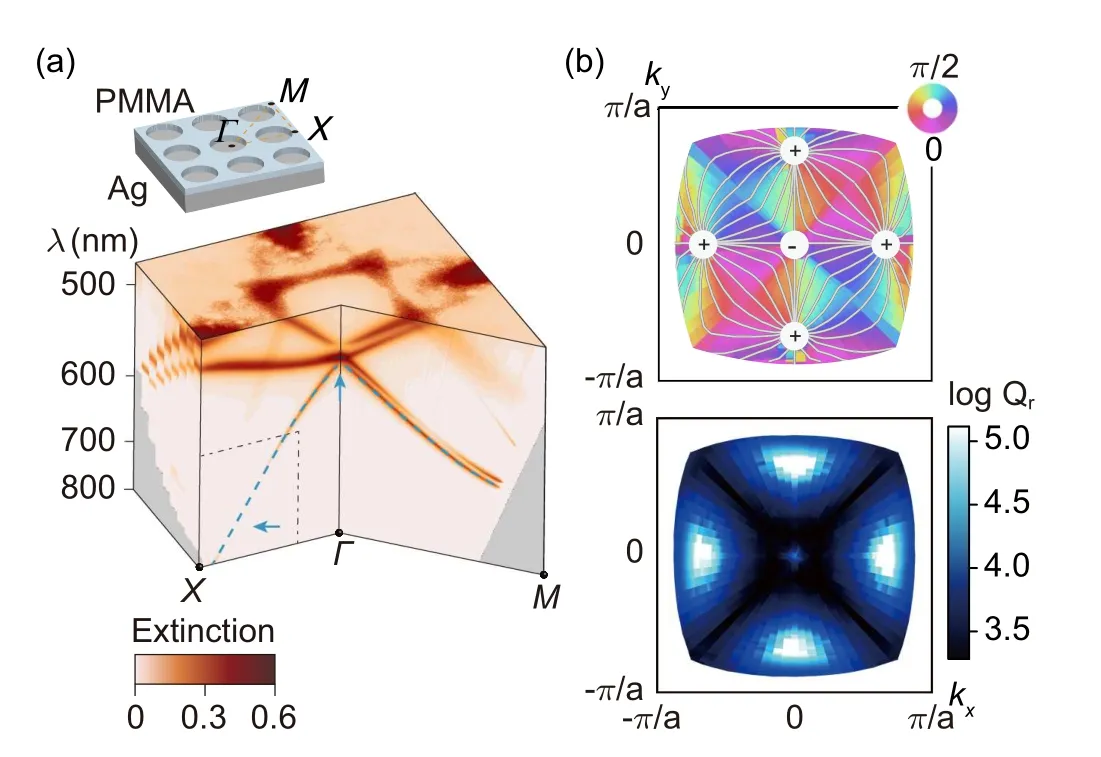
Fig. 3. First experimental observation of momentum-space polarization fields and singularities. (a) Measured momentum-space extinction spectra of a plasmonic crystal consisting of a periodically structured PMMA thin film with a square lattice of holes on a silver surface. (b)Momentum-space polarization field(upper panel)and the corresponding quality-factor map reconstructed from the measured data(lower panel). Five V-points exist in the first Brillouin zone.[43]

Most theoretical and experimental studies on V-points are for non-degenerate resonant modes. However,there exist also degenerate points in photonic bands in momentum space. The question arises whether V-points exist at degenerate points of photonic bands. Indeed, as a superposition of modes, a degeneracy itself is a singularity in some sense, which should result in singular polarization states such as V-points in momentum space. In 2019, Chenet al.[47]studied a plasmonic structure withC4vsymmetry and discussed V-points at theΓpoint where two TM-like bands are quadratically degenerated.They mapped out the polarization field on the two bands and confirmed the existence of V-points of charge±1 both theoretically and experimentally,as shown in the upper-right panel of Fig. 4. Exactly at these degenerate V-points, the polarization states are ill-defined as expected.However,their radiation amplitudes are non-zero,different from non-degenerate V-points.Radiations resulting from these modes can have arbitrary polarization states depending on how they are excited externally.

Fig. 4. Different types of momentum-space polarization singularities and their connections. Upper-left panel: a non-radiative integer-charged V-point protected by in-plane Cn (n ≥2)symmetry,corresponding to a BIC.Upperright panel: a radiative integer-charged V-point at the degenerate point of two quadratic photonic bands for an in-plane Cn (n ＞2)symmetry. Lowerleft panel: two C-points with half-integer charges and opposite handedness separated by an L-line. Lower-right panel: two radiative V-points with halfinteger charges at two linearly degenerate points(Dirac points or bulk Fermi arcs).

Although both the non-degenerate and degenerate Vpoints at theΓpoint discussed above are protected byC4vsymmetry,they differ not only in radiation properties but also in their responses to symmetry perturbations. When the symmetry is broken to beC2, a non-degenerate V-point is no longer stable, whereas a degenerate V-point is not the case.As illustrated in the right panels of Fig. 4, a degenerate Vpoint of charge±1 is decomposed into a pair of V-points with half-integer charges±1/2, corresponding to the process of a quadratic degeneracy splitting into two Dirac points[47,48](or bulk Fermi arcs when considering a small non-Hermitian perturbation[49]). The linearly degenerate states at the vortex centers are radiative although ill-defined. Such V-points with half-integer charges are closely related to linear degeneracies under any circumstances since their half-integer charges result from aπBerry phase associated with the corresponding degenerate points.[50–52]Note that V-points with half-integer charges are the lowest order of degenerate V-points, but not yet confirmed experimentally.

From the theory of singular optics,V-points in real space are not the most robust and fundamental singularities,and are usually protected by some specific symmetries. By breaking the symmetry of a field,V-points can be turned into other types of polarization singularities(e.g.,C-points separated by L-lines), and vice versa.[20,22]In momentum-space polarization fields, V-points are also sensitive to symmetry perturbations. As indicated by Liuet al.,[44]non-degenerate V-points located at and away from theΓpoint are both sensitive toC2symmetry breaking, illustrated in the left panels of Fig.4.When theC2symmetry of a PhC slab is broken, an existing V-point with charge±1 will be decomposed into a pair of C-points with opposite handedness and half-integer topological charges. An L-line will appear in between the two Cpoints with opposite handedness,required by the continuity of the polarization fields. In addition, they found a similar process by breaking the up-down mirror symmetry of a photonic structure with two open boundaries. On the other side, for degenerate V-points Guoet al.[51]studied the effect of symmetry perturbations on degenerate V-points with half-integer charges. Several V-points with half-integer charges are obtained at the corner of the first Brillouin zone for a PhC slab withC3vsymmetry. By slightly breaking theC2symmetry,the Dirac degeneracies will be lifted. As a result,each degenerate V-point with a half-integer charge will become a C-point with the same charge,schematically illustrated in the lower panels of Fig.4.

Thus, the scenario of the evolutions for V-points with charge±1 in momentum-space polarization fields are as follows. A non-degenerate V-point protected byC2,Cnor other symmetries will be decomposed into a pair of C-points separated by an L-line when breaking the symmetry. On the other hand, a degenerate V-point with charge±1 will be split into two V-points with charge±1/2 when perturbing theCn(n=4 or 6)symmetry intoC2. V-points with half charges can further become C-points with the same charges by breaking the remainingC2symmetry. Note that all topological charges are conserved during these evolutions.

The V-points with topological charges of high-order(|q|＞1) may exist in momentum-space polarization fields.For instance, a high rotational symmetry such asC6vcan give rise to both non-degenerate and degenerate V-points with a topological charge of-2 in a PhC slab.[9,43]Evolutions of both non-degenerate and degenerate higher-order V-points upon symmetry breaking were investigated respectively by Yodaet al.[53]and Chenet al.[47]in different systems, summarized in Fig.5.

Distinctly different from the case of|q|=1, both nondegenerate and degenerate higher-order V-points are both nonradiative, i.e., BICs. However, their response to symmetry breaking is different. For non-degenerate higher-order Vpoints,with symmetry breaking fromC6vtoC2va V-point with charge-2 will be split into two V-points with charge-1 away from theΓpoint,as illustrated in the middle in Figs.5(a)and 5(b). Whereas for the quadratically degenerate V-point with charge-2,it will be decomposed into one non-degenerate Vpoint with charge-1 and a pair of degenerate V-points with charge-1/2,as shown on the right in Figs.5(a)and 5(b). The V-point with charge-1 remains at theΓpoint and is still nonradiative. The pair of degenerate V-points with charge-1/2 correspond to two Dirac degeneracies.

Fig.5. Momentum-space polarization fields with polarization singularities in a 2D PhC slab with an array of holes arranged in a hexagonal lattice for different in-plane symmetries. For a 2D PhC slab with in-plane symmetry of C6 in (a), both non-degenerate or singlet (middle) and quadratically degenerate(right)V-points of charge-2 at the Γ point could exist. When the in-plane C6 symmetry is reduced to C2 in(b),the singlet V-point of charge-2 will be split into two V-points of charge -1 (middle), whereas the degenerate V-point will become one V-point of charge-1 and two V-points of charge-1/2. When the in-plane symmetry is changed from C6 to C3 in(c),both the singlet V-point and the degenerate V-point will be decomposed into six C-points of charge-1/2 and one V-point of charge+1.

On the other hand, if the symmetry is broken fromC6vtoC3v, the singlet V-point with charge-2 would be turned into a non-radiative V-point of charge +1 at the same location of theΓpoint surrounded by three pairs of C-points with opposite handedness rather than three V-points, as shown in the middle in Fig. 5(c). This is due to fact that the existence of V-points away from theΓpoint is generally forbidden for a system withoutC2symmetry. The total charge of these Cpoints should be-3 required by the charge conservation. The evolution is schematically illustrated in the left of Fig. 5(c).For the degenerate V-point of charge-2,the evolution is similar to the singlet case. Since the quadratic degeneracy cannot be lifted with such type of symmetry breaking,the resulting Vpoint will be a degenerate one and hence radiative, as shown on the right in Fig.5(c).

Further symmetry perturbations by breaking theC2orC3symmetry will result in the evolutions discussed in the above for|q|=1 cases. Interestingly,Cheet al.[54]showed that a Vpoint with charge|q|≥3 can exist in photonic quasi-crystals slabs. Evolutions of those V-points follow the same rules described above. Besides, there may be dissociative C-points far away from V-points in momentum space due to complex mode interactions even if theC2symmetry is maintained, as discussed by Yeet al.[50]

Up to now, most studies on momentum-space polarization fields are for photonic structures with time-reversal symmetry. In recent work, Songet al.[55,56]studied theoretically polarization singularities in photonic systems with parity-time symmetry,revealing a new type of non-radiative V-points,i.e.,pt-BICs which can be excited externally but can not radiate.

4. Applications

Momentum-space polarization fields on photonic bands of a PhC slab could be engineered by properly choosing the structural and material parameters, leading to interesting applications to be discussed in the following.

4.1. Increasing robustness of high-quality-factor resonances

As discussed in the above section,a singlet or high-order degenerate V-point in momentum space defined on a photonic band corresponds to a non-radiative state if the only radiation channel is blocked by the V-point. These V-points can suppress radiations in their vicinity in momentum space.As a result, the corresponding resonances possess ultra-highQfactors,[11]leading to low radiation loss for zero-index materials,[57,58]low thresholds in lasing actions[59–63]and enhanced optical non-linear processes.[64–68]From the practical point of view, structural or material imperfections are nearly inevitable during fabrications and eventually cause degradations inQfactors, due to unexpected scatterings and the fact that V-points are sensitive to symmetry perturbations.

To overcome this problem,Jinet al.[69]proposed that the robustness of high-Qresonances can be greatly retained by merging multiple non-radiative V-points in momentum space,shown in Figs. 6(a) and 6(b). Focusing on the second TElike band of aC4vsymmetric PhC slab made of silicon, they changed the period of the slab to manipulate the distributions of V-points in momentum space.With theC4vsymmetry,there will always be one V-point at theΓpoint. When the period is not well tuned [right panel in Fig. 6(a)], this V-point is isolated and theQfactor decays quadratically in its vicinity. As a result,fabrication imperfections can easily degrade the high-Qfeature by scattering to other resonances away from theΓpoint. The symmetry perturbations could make the problem worse. If the period is chosen in a proper range, eight Vpoints will appear around the V-point at theΓpoint, leading to eight additional high-Qregions in momentum space. With the period carefully tuned, the eight V-points will approach the V-point at theΓpoint, leading to a large high-Qregion in momentum space. Away from the merged region, theQfactor decays inversely proportional to the sixth power of the in-plane wavevector. Under this circumstance, theQfactors of resonances are much less affected by unexpected scatterings. Symmetry perturbations should be less destructive either since the C-points spawning from one V-point may easily collide with other emerging C-points. The merging processes of V-points are shown in the left and middle panels of Fig.6(a).The scattering suppressing effect due to the merging V-points was also confirmed,as shown in Fig.6(b). Clearly,radiations from the resonances with non-zero in-plane wavevectors in a disordered structure with merging V-points are much smaller than those in a structure with an isolated V-point, leading to much higherQfactors even in the presence of fabrication imperfections. The robust ultra-highQfactors are of great significance in practical applications.

Fig. 6. Increasing robustness of high-Q resonances by merging multiple non-radiative V-points in 2D PhC slab. (a) Merging multiple V-points around the Γ point. On one photonic band, eight V-points are shifted towards the central V-point at the Γ point,resulting in a large high-Q region.(b) Distributions of the momentum-space radiation field for a disordered isolated-BIC(left)and merging BICs(middle). The corresponding Q values simulated are plotted on the right. (c)Merging multiple V-points away from the Γ point. One V-point is shifted towards another off-Γ V-point, leading to a large high-Q region.[69,70]

Note that the V-point merging scheme to increase the robustness of high-Qresonances relies on their numbers rather than their topological charges. In the above work,eight accidental V-points which appear symmetrically near theΓpoint were chosen for merging. Such a scheme can be generalized to other situations,e.g.,by merging multiple non-radiative Vpoints with lower symmetry. Kanget al.[70]showed that Vpoints resulting from different coupling mechanisms can be merged as well in order to increase the robustness of high-Qresonances with large in-plane wavevectors. The authors designed aC4v-symmetric silicon-nitride PhC slab immersed in a liquid. The structure has a V-point located in theΓ–Mdirection, stemming from the coupling between the third and the fifth TM-like photonic bands. By tuning the thickness of the slab, another accidental V-point appears. The two V-points will approach each other for a proper choice of the thickness, leading to a large high-Qregion, as shown in Fig. 6(c). Furthermore, the authors showed a more generalized case where two V-points can be merged at an arbitrary in-plane wavevector in aC2-symmetric PhC slab. They also showed that V-points with higher order topological charges can be merged,[71]rendering more flexibility possible. This generalized V-point merging scheme seems more appealing in both lasing actions and non-linear processes by offering more degrees of freedom in the selection of wavevectors,e.g.,directional radiations.

4.2. Guided resonances with unidirectional radiations

For a 2D periodic photonic structure with two open boundaries,there are two radiation half-spaces,corresponding to two outside regions of the structure.In general,the radiation properties of supported modes such as polarization states are different in the two half-spaces. A non-radiative mode with a in-plane wavevectork‖,namely,a BIC,requires that all the radiation channels in both half-spaces should be blocked by V-points. In order to achieve this condition, there are usually two prerequisites. First,there shall be no other diffraction order, i.e., all possible|k‖+G|(forG/=0)are larger than the free-space wavevector|k0|in both radiation half-spaces.Thus,only one V-point is required for each radiation half-space.Second, there should be an up–down mirror symmetry and a rotational symmetry so that the two radiation half-spaces are related to each other. As a result,the required V-points can exist and appear at the samek‖in both half-spaces.

An interesting question arises whether it is possible to block only one of the two radiation channels by a V-point.In other words, it is a unidirectional BIC with radiations allowed in one half-space but forbidden in the other. Indeed,Yinet al.[72]reported such a mode in a grating structure which radiates only in one half-space,as shown in Fig.7(a). This interesting mode was dubbed unidirectional guided resonance.They started from a grating consisting of dielectric bars with a rectangular cross section which supports an off-ΓBIC. By tilting one side of the rectangles, the perturbation on the up–down mirror andC2rotational symmetries is increased. By inspecting the momentum-space polarization field defined on the second TE-like band in the lower radiation half-space,the off-ΓV-point (a BIC) is decomposed into a pair of C-points with opposite handedness when the symmetries are broken.The two C-points are located mirror-symmetrically near theky=0 axis, following the symmetry of the structure. Their trajectories in momentum space are plotted in Fig.7(b). With the tilting angle increasing,the two C-points firstly move away from theky=0 axis and then come closer. When the basing angle reaches 75°, the two C-points accidentally meet each other, merging back into one V-point. In this situation, only the radiation channel in the lower half-space is blocked by the presence of the V-point, leading to a unidirectional radiation.As for experimental verifications, the authors used a grating consisting of bars with an obtuse-trapezoid cross section situated on a substrate.With the proper tilting angles of side walls,a unidirectional guided resonance was found. This mode cannot couple with modes in the lower radiation half-space.However,it can be excited and observed in the upper half-space.

Fig.7. Realization of unidirectional guided resonances by merging C-points in gratings without up–down mirror symmetry. (a)Grating consisting of dielectric bars with a right-angled trapezoid cross section and(b)charge evolutions with the basing angle θ. (c)Bilayer grating and(d)charge evolutions with the misalignment.[72,73]

A double-layer grating structure was adopted by Zenget al.[73]to realize unidirectional radiations, as shown in Fig.7(c). The two layers have the same structural and material parameters but are misaligned to perturb theC2and up–down mirror symmetries. The inversion symmetry remains so that the momentum-space polarization fields in the upper and lower radiation half-spaces are inversion-symmetric. With the misalignmentδchanged from 0 to 0.11a(ais the period),the momentum-space polarization field defined on the fourth TElike photonic band in the lower radiation half-space will evolve accordingly. The trajectories of C-points near theΓpoint are shown in Fig.7(d). The evolution starts from the spawning of two pairs of C-points which are mirror-symmetric about theky=0 axis with opposite handedness. For each pair of Cpoints,the total topological charge should be 0 as they spawn from scratch. Withδincreasing, the C-points with charges-1/2 and +1/2 will move towards different directions. Interestingly,two of the four C-points,with topological charges-1/2, will regroup and merge into one V-point twice during the evolution. Imposed by the mirror symmetry, the emerging V-points are always located on theky=0 axis. The first merging occurs whenδ=0.0674a,leading to a unidirectional guided resonance with non-zero wavevector,whereas the second merging occurs whenδ=0.092aat theΓpoint. Because of the inversion symmetry, such a V-point at the inversioninvariantΓpoint produces a truly accidental BIC.

Other schemes for realizing unidirectional guided resonances and increasing their robustness were proposed.[74]Unidirectional radiations caused by unidirectional guided resonance can have important applications in case that scattering of a guided mode towards one specific half-space needs to be maximized or prohibited,e.g.,the design of augmented reality glasses.Moreover,based on unidirectional guided resonances,exotic applications such as unidirectional luminescence and fluorescence,and mirrorless lasing could be realized.

4.3. Non-local meta-surfaces

Meta-surfaces are structures which can modulate electromagnetic waves within a deep-sub-wavelength dimension.[75–80]Conventional meta-surfaces are composed of space-varied resonators acting as building units and can used to redistribute the intensity profile, reshape the wavefront, and convert the polarization field of incident waves.Moreover, singular beams with intensity singularities (e.g.,Airy beams[81]),phase singularities(e.g.,vortex beams[82,83]),and polarization singularities(e.g.,vector beams[84,85])can be generated.

Physically,modes supported in PhC slabs can be viewed as resonances in momentum space. Similar to conventional meta-surfaces, different momentum-space resonances can be combined to construct a new type of meta-surfaces: nonlocal meta-surfaces.[86–93]Obviously, these non-local metasurfaces can perform optical functionality as a whole,relying on momentum-space-varied resonances rather than real-spacevaried resonators. In this sense, they can be called non-local.PhC slabs can provide with rich optical features in momentum space for constructing non-local meta-surfaces,leading to many interesting phenomena and novel applications,e.g,freespace squeezing based on resonant phase changes induced by a PhC slab.[89,90,92]

Guoet al.[86,87]reported that arbitrary polarization conversions from arbitrarily polarized incidence light can be realized by a PhC slab as a non-local meta-surface in the reflective mode, as shown in Fig.8(a), based on a V-point at the center of momentum space defined on the second TE-like photonic band. For a frequency in the range of the band, there exist wavevectors to guarantee that a linear polarization state can be completely converted into the orthogonal polarization state.Such wavevectors also appear to be topological singularities in momentum-space vector fields formed by the real and imaginary parts of the cross-polarization reflection coefficient. The topological nature of these wavevectors ensures that polarization conversions from linear to arbitrary polarization states can be achieved. The authors further proved the arbitrary polarization conversion from elliptical polarizations. Note that such a polarization converter is angle-dependent. A PhC slab as a non-local meta-surface can also be applied to modulate the polarization of photon emission.[94–96]

Fig. 8. Non-local meta-surfaces based on 2D PhC slabs. (a) Arbitrary polarization conversion. An incident polarization state can be converted into a desired polarization state simply by changing the incident angle. (b)Optical vortex beam generated non-locally. (c)Transverse beam shifting at normal incidence. The outgoing light beam will undergo a transverse shift after traversing.[86–88,93]

Cross-polarization conversions of light by an optical element can give rise to a geometric phase, namely, a Pancharatnam–Berry (P-B) phase.[97–101]Thus, conventional meta-surfaces can be designed to modulate wavefronts using P-B phases.[78,85,102,103]The same principle can also be applied to non-local meta-surfaces made of PhC slabs.[88,93]In momentum space, wavevector-varied resonances with different polarization states play a role of momentum-space polarization converters. As a result, a momentum-space polarization field will result in a distribution of momentum-space P-B phases, which could offer new perspectives for light manipulations.

The first non-local meta-surface based on momentumspace P-B phases, as far as we know, was proposed and realized by Wanget al.[88]Momentum-space polarization fields of a 2D PhC slab with non-radiative V-points in the center were exploited to generate beams with spiral phase fronts, as shown in Fig.8(b).When a para-axial and circularly-polarized beam is normally shined on the PhC slab, the winding polarization states around the V-points can induce phase vortices in the outgoing cross-polarized beam in momentum space. The topological charges of the phase vortices are±2q,whereqis the charge of the V-points and the sign is determined by the handedness of the incident light. Such phase vortices exist in both momentum and real spaces. Consequently, the outgoing beams will have spiral wavefronts. The authors confirmed numerically the vortex generations in two 2D PhC slabs, one withC4vand the other withC6vsymmetry. Vortex beams with topological charges±2 and?4 were generated by Vpoints with charge+1 and-2,respectively. Generated vortex beams were directly observed and measured experimentally.Note that the generated beams are quasi-Bessel beams which are diffraction-resistant due to the momentum-space amplitude modulations.

Another realization of non-local meta-surfaces based on P-B phase was carried out by Wanget al.,[93]based on the momentum-space phase gradient induced by a momentumspace polarization field rather than the phase profile itself. In real space, an extra phase gradient?φ(r‖)/?r‖induced by a conventional meta-surface will result in a displacement in momentum space,[40,75]given by

To achieve a desired phase gradient, a free-standing 2D PhC slab withC1hsymmetry(an array of isosceles-triangular holes in a silicon-nitride slab)was designed, as shown in Fig.8(c).In the polarization field defined on the second TE-like band,there appear a pair of C-points separated by an L-line near theΓpoint. Due to the symmetry, the two C-points are mirrorsymmetric to each other about thekx=0 line,while the L-line lies on the mirror axis. Such a polarization field can result in a net P-B phase gradient in thekxdirection when the incoming light is±45°polarized and the outgoing light is analyzed with a?45°polarizer. Thus,if a beam with±45°polarization is normally shined on the PhC slab, the outgoing beam with?45°polarization will be shifted transversely owing to the introduced phase gradient. Fabrications and measurements were also conducted,confirming the proposed idea.

Non-local meta-surfaces based on P-B phase modulations show some interesting features that conventional meta-surface do not possess. For instance, they are periodic structures without geometric centers since their optical functionality relies totally on momentum-space resonances. In other words,no optical alignments are needed unlike many optic devices and conventional meta-surfaces. This shows again the nonlocality of non-local meta-surfaces. Other interesting studies based on momentum-space P-B phase modulations were also conducted.[104–106]

5. Conclusions and outlook

In this review, we briefly discuss the recent research progress on momentum-space polarization fields in periodic photonic structures with open boundaries, mainly focusing on 2D PhC slabs. Momentum-space polarization fields display complicated configurations and patterns stemming from the radiation polarization states of Bloch modes on photonic bands.

Different types of polarization singularities such as Vpoints, C-points, and L-lines appear in momentum-space polarization fields,strongly depending on structural symmetries.Interestingly, V-points could evolve into other V-points with different topological changes or even into C-points via symmetry perturbations or structural changes,and vice versa.

Momentum-space polarization fields and singularities inside could offer new perspectives in exploring the optical response of PhCs and novel applications as well. Indeed,by merging V-points a large region in momentum space with robust high quality factors against structural imperfections can be obtained, practically meaningful to realize lowthreshold lasing and enhanced nonlinear processes. With mirror-symmetry breaking, it is possible to obtain unidirectional radiations based on different behaviors of V-points in two radiation half-spaces. Momentum-space polarization fields can also be exploited to realize non-local meta-surfaces for beam steering such as polarization conversion,vortex beam generation,and beam shifting.

Momentum-space polarization fields defined on photonic bands in periodic photonic structures with open boundaries are an emerging field. Despite many progresses made in recent years, there remain still many interesting problems that need further study, such as what key factors determine the configurations and patterns of polarization fields and singularities,evolutions and dynamics of V- and C-points including their creation, conversion, collision, and annihilation. Impact of time-reversal symmetry or/and Lorentz reciprocity breaking is also an interesting topic. Extra dimensions such as time could be incorporated to construct more complicated polarization fields in higher-dimensional parametric space,leading likely to novel types of polarization fields and singularities.

Acknowledgements

The work was supported by the National Natural Science Foundation of China (Grant Nos. 11727811 and 91963212),the National Key Basic Research Program of China (Grant No. 2018YFA0306201), and Science and Technology Commission of Shanghai Municipality(Grant Nos.19XD1434600,2019SHZDZX01,19DZ2253000,and 20501110500).