Invariable mobility edge in a quasiperiodic lattice
Tong Liu(劉通) Shujie Cheng(成書(shū)杰) Rui Zhang(張銳)Rongrong Ruan(阮榕榕) and Houxun Jiang(姜厚勛)
1School of Science,Nanjing University of Posts and Telecommunications,Nanjing 210003,China2Department of Physics,Zhejiang Normal University,Jinhua 321004,China
We analytically and numerically study a 1D tight-binding model with tunable incommensurate potentials. We utilize the self-dual relation to obtain the critical energy,namely,the mobility edge. Interestingly,we analytically demonstrate that this critical energy is a constant independent of strength of potentials. Then we numerically verify the analytical results by analyzing the spatial distributions of wave functions,the inverse participation rate and the multifractal theory.All numerical results are in excellent agreement with the analytical results.Finally,we give a brief discussion on the possible experimental observation of the invariable mobility edge in the system of ultracold atoms in optical lattices.
Keywords: Anderson localization,quasiperiodic,mobility edge,multifractal
1. Introduction
Anderson localization,[1]a universal phenomenon of wave propagation in disordered mediums,is an active research subject in condensed matter physics. With regard to the disordered systems,the scaling theory[2]predicts that delocalizedlocalized transitions are known to arise in dimension strictly higher than two. In one- and two-dimensional systems, uncorrelated random disturbances account for why all the wave functions are exponentially localized. Accordingly, in lowdimensional disordered systems, there is always a hot topic,namely the delocalization-localization transition. There is an energy level threshold which separates the delocalized functions from those are localized. This critical energy is known as the mobility edge.However,it is still a challenge to observe the mobility edge in three-dimensional(3D)systems with the mobility edge in experiment.[3–9]Therefore, to acquire more insights into the mobility edge and uncover its essence, lowdimensional systems,such as 1D quasiperiodic systems,are a better choice. After all,there has been a long history to search the systems with mobility edge and plenty of theoretical models are proposed and studied in decades.[10–23]Moreover, the mobility edge has been observed in recent experiments by manipulating the cold atoms trapped in 1D quasiperiodic optical lattice[24,25]although a precise measurement of its value is still lacking.
The Aubry–André (AA) model[26]plays an important role to understand the Anderson localization and uncover the mobility edge. As a paradigmatic 1D tight-binding model,the AA model has a self-dual symmetry, and the increasingly incommensurate potential will make the system undergo a localization transition,from the extended phase to the localized phase.[27]Moreover, the mobility edge always appears in the extended AA models. For instance,Das Sarmaet al.revealed that there was mobility edge in a class of systems with slowvarying incommensurate on-site potentials.[10–12]Biddleet al.found the exactly solvable mobility edge in the extended AA model with long-range tunnelings.[13,14]Ganeshanet al.verified the existence of the mobility edge which was protected by the self-dual symmetry.[15]Liuet al.obtained the exactly solvable mobility edge in the off-diagonal incommensurate models.[16,17]Nowadays,the research about the mobility edge has been extended to the non-Hermitian case,[28–30]where the mobility edges were located in the real energy spectra. However,by comprehensively analyzing the above research results on mobility edge,we find that the mobility edges change with the extra parameters that are commonly the strength of the incommensurate on-site potentials. We cannot help but ask,is it a universal phenomenon that the mobility edge changes with the extra parameters? Is there a special case where the mobility edge is a constant that is a bit easier to measure experimentally?
In this work,we are motivated to study a 1D tight-binding model with tunable incommensurate potentials. We make attempt to find out whether there is a mobility edge which keeps a constant in this model and then extract it analytically, if it exists. We further verify the analytical result by the inverse participation rate and the spatial distributions of the wave functions.
The rest of this paper are arranged as follows:In Section 2 we present the model and derive the mobility edge by the selfdual relations. In Section 3 we verify the analytically obtained mobility edge by the inverse participation rate and the distributions of the wave functions. Finally,we make a summary in Section 4.
2. Model and the mobility edge
In this section,we consider a 1D tight-binding model with nearest-neighbor hoppings and incommensurate on-site potentials,and we are devoted to extract the mobility edge analytically. The static Schr?dinger equation is written as
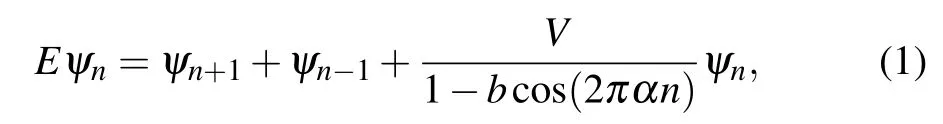
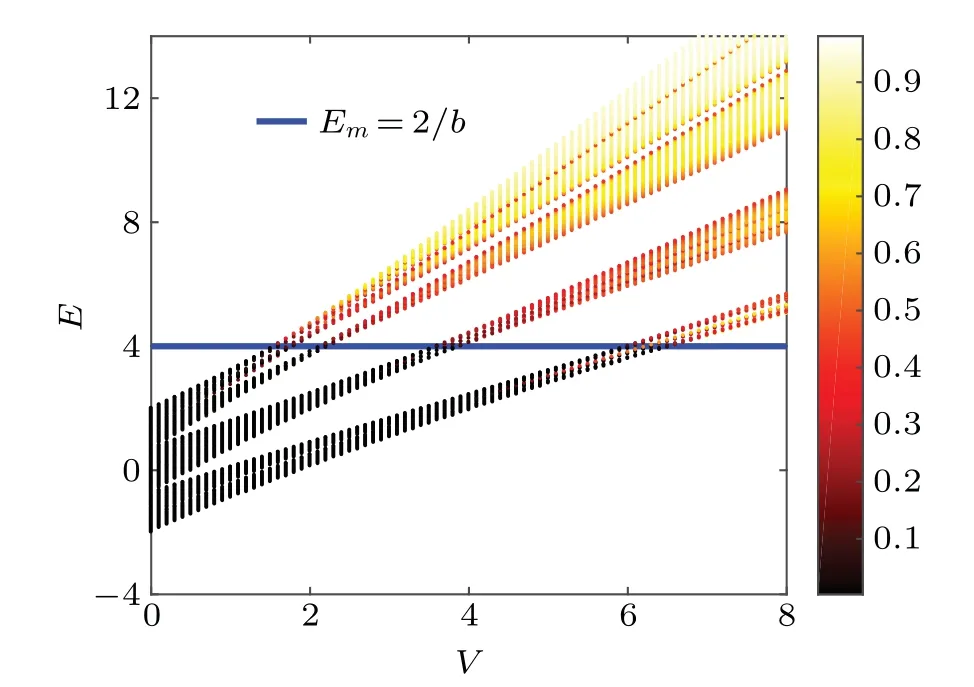
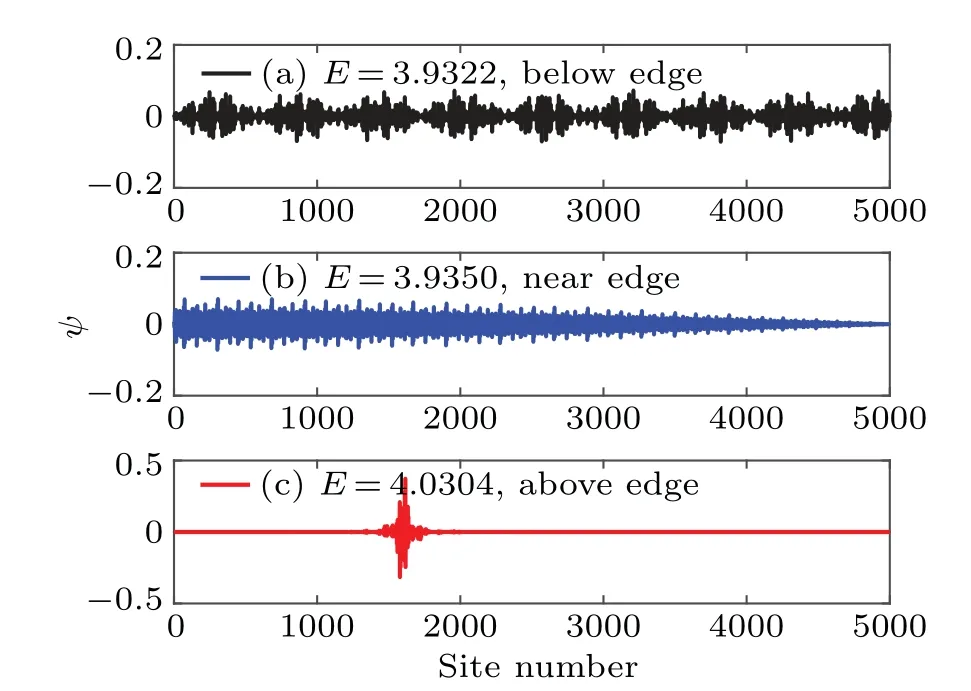
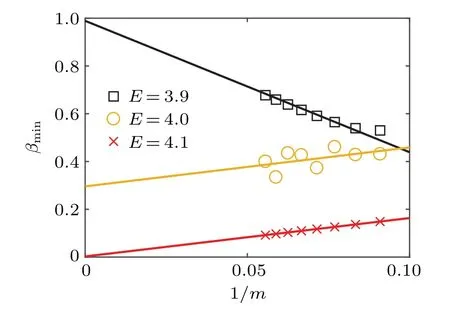
whereVis the potential strength with 0 Next, we introduce some self-dual relations, which are necessary in the following derivation: wheresands0are real constants. Therefore, Eq. (2) can be rewritten as Then, we multiply both sides of Eq. (4) byΩk(s0)ei2παmk,and sum it overm. After defining the relationshipφk=∑mei2παmkΩm(s)φm, Eq. (4) is further expressed as We continue multiplying both sides of Eq.(5)by ei2παkq,and summing it overk. By defining the relationshipμq=∑kei2παkqφk,Eq.(5)is transformed into Note that whens=s0,Eq.(3)is reduced to Eq.(1). From the self-dual relations cosh(s)=1/bandE=2cosh(s), we obtain the mobility edge Interestingly,for a fixed value of the tuning parameterb,Ecis independent of the potential strengthV. The property of“being constant”of the mobility edge is a intriguing result. In the following,we will check the predictions ofEcin the theoretical analysis by direct numerical simulations,so as to make the theoretical analysis convictive. In this section,we verify the accuracy of the analytically obtained mobility edgeEcby exhaustively numerical analysis. In order to acquire the eigenenergiesEof the system and the associated wave functionsψ, we numerically diagonalize the model’s Hamiltonian which is defined in terms of the Schr?dinger equation in Eq. (1). Then, it is convenient to calculate other typically physical quantities that are needed in our numerical validation. For example, the inverse participation rate and the spatial distributions of the wave functions will be used to distinguish the extended and localized states.Although our numerical simulations are carried out at the system with finite size,our results are exactly consistent with the theoretical analysis under the thermodynamic limit. To begin with,we calculate the inverse participation rate(IPR).As it was studied in Ref.[31],the IPR of a given wave functionψis defined as whereψhas been normalized,Lis the total number of the lattice sites, andjdenotes the energy level index. It is widely known that for the extended wave functions, the corresponding IPRs scale likeL?1,which tend to 0 whenL →∞,whereas they keep finite values for localized states. Fig.1. The eigenvalues of Eq.(1)and IPR as a function of V with the parameter b=0.5.The total number of sites is set to be L=500.Different colors of the eigenvalue curves indicate different magnitudes of the IPR of the corresponding wave functions. The black region where the IPR approaches zero denotes the extended states,and the orange region with a whitish hue where the IPR tends to 1 denotes the localized states.The blue solid line represent the boundary between spatially localized and extended states,i.e.,the mobility edge Ec=2/b=4. Figure 1 is the energy spectrum which exhibits variation of eigenenergiesEas a function of the parameterV, where we have considered the size of the system isL= 500 and the tuning parameterb=0.5. As shown in Fig. 1, the spectrum is not a single band but consists of several bands. The color shows the IPR of the corresponding eigenenergy. Concretely,the black region where the IPR approaches zero means the wave functions that these eigrnenergies correspond to are all extended. On the contrary,the orange region with a whitish hue where the IPR tends to 1 means the wave functions that these eigen-energies correspond to are all localized. Intuitively,there is a critical energyEc=4 separating the extended states and the localized states. The result of this numerical analysis is consistent with what the theoretical analysis predicts. In order to have an intuitive insight into the separation in the aspect of energy,we plot the spatial distributions of associated wave functions,whose corresponding eigenenergies are nearEc.Before performing the numerical calculation,we have specified that the required parameters areb=0.5,V=3.8 andL=5000. We choose three typical wave functions whose corresponding eigenenergies are above,below or close to the mobility edgeEc=4. Figure 2 shows the spatial distributions of the four wave functions,in which Fig.2(a)is intuitively seen that the wave function is extended, whose corresponding energy is belowEc=4.On the contrary,Fig.2(c)is the localized states,whose corresponding energy is aboveEc=4.More impressive,the eigenenergy of Fig.2(b)is closed toEc=4 and can be seen as be neither localized nor extended over the whole space,instead,it displays the characteristic of the critical state. Fig.2. Wave functions obtained from Eq.(1)with b=0.5,V =3.8 and L=5000 nearby the mobility edge Ec =4. Three different eigenenergies: (a)low energy extended state below the mobility edge,(b)critical state near the mobility edge, and (c)high energy localized state above the mobility edge. To further verify the reliability of the analysis results of IPR and wave functions,we use the multifractal theory,which has been widely applied to standard quasiperiodic models.[32]For each wave function,a scaling exponentcan be extracted from thenth on-site probabilityAccording to the multifractal theorem, when the wave functions are extended, the maximum ofscales as. On the other hand, when the wave functions are localized,peaks at very few sites and nearly zero at the other sites,yielding. As for the critical wave functions,the correspondingis located within the interval (0,1),and can be used to discriminate extended and critical states. In order to reduce finite-size effects, we useto distinguish different wave functions in numerical calculations. Figure 3 plotsβminas a function of the inverse Fibonacci index 1/m. It clearly shows thatβminis between 0 and 1 in the largeLlimit for the eigenenergyE=4.0, hence suggesting that wave functions closed to the mobility edge are critical. However, for the eigenenergyE=3.9,βminasymptotically tends to 1 in the thermodynamic limit, indicating that the corresponding wave function is extended. Conversely,for the eigenenergyE=4.1,βminasymptotically tends to 0 in the thermodynamic limit, indicating that the corresponding wave function is localized. Thus,the above numerical results are in excellent agreement with the analytical results. We have also checked other combinations of parameters and get the same results as expected. Fig. 3. Behavior of βmin as a function of the inverse Fibonacci index 1/m for various eigenenergies when V =3.75. The brown markers correspond to the critical state with E=4.0 closed to the mobility edge Ec,the black markers correspond to the extended state with E =3.9 below the mobility edge Ec, and the red markers correspond to the localized state with E=4.1 above the mobility edge Ec. Finally, we would like to point out that this invariable mobility edge can be realized in the ultracold-atom experiment. Using synthetic lattices of laser-coupled atomic momentum modes, the authors of Ref. [33] experimentally realized a recently proposed family of nearest-neighbor tightbinding models having quasiperiodic site energy modulation that host an variable mobility edge protected by a duality symmetry. The experimental method in this paper is based on momentum space lattice tuning. The on-site potential at each lattice point in momentum space is equal to the detuning of Raman coupling between different momentum states, hence the on-site potential form required for the precise modulation of these detuning to match is obtained. Alternatively, we can utilize synthetic dimension to simulate this type of on-site lattice. For example,we can use each spin state of large spin atoms (such as Dy atoms) as lattice points,and use Raman Coupling to couple adjacent spins(i.e.,the coupling of adjacent lattice points), then realize the onsite potential by controlling the detuning property of Raman coupling.[34–36] In conclusion,we have studied a 1D tight-binding model with tunable quasi-periodic potential. It is revealed that there exists mobility edge in this model, and its analytical expression is obtained by the self-dual relations. Surprisingly,unlike previous studies,the mobility edge in our model keeps invariable with the strength of the potential, which is only determined by the control parameterb. This finding may contribute to a more convenient observation of the mobility edge in the future experiment. Detailed numerical analyses, such as the inverse participation rate and the spatial distributions of wave functions,demonstrate that our results are reliable. Acknowledgements T. Liu acknowledges X.-J. Liu for fruitful discussion.This work was supported by the Natural Science Foundation of Jiangsu Province, China(Grant No.BK20200737), NUPTSF(Grants Nos. NY220090 and NY220208), and the National Natural Science Foundation of China (Grant No. 12074064),and the Innovation Research Project of Jiangsu Province,China (Grant No. JSSCBS20210521), and NJUPT-STITP(Grant No.XYB2021294).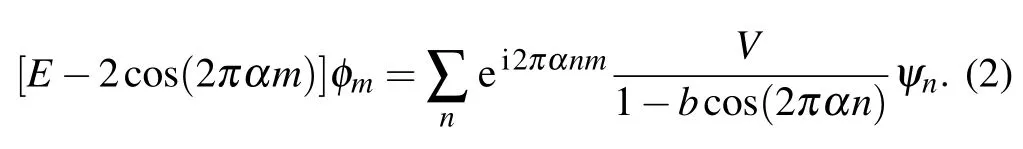

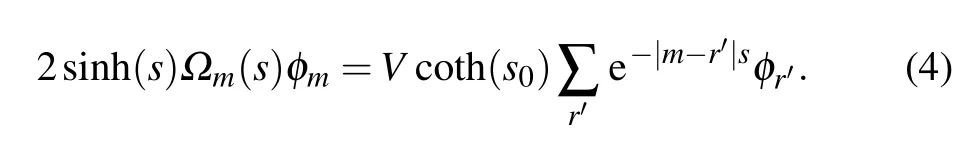
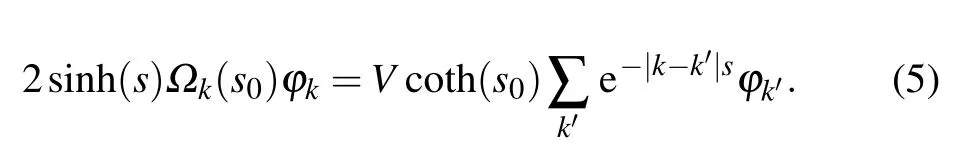
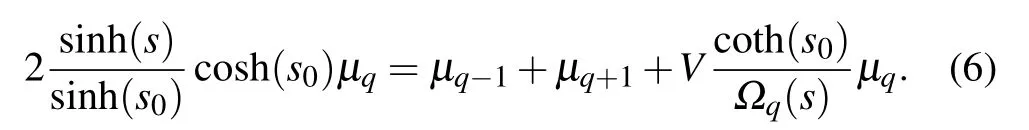

3. Numerical results and discussions

4. Summary
- Chinese Physics B的其它文章
- A broadband self-powered UV photodetector of a β-Ga2O3/γ-CuI p-n junction
- High-sensitive terahertz detection by parametric up-conversion using nanosecond pulsed laser
- High efficiency,small size,and large bandwidth vertical interlayer waveguide coupler
- High-fidelity resonant tunneling passage in three-waveguide system
- An analytical model for cross-Kerr nonlinearity in a four-level N-type atomic system with Doppler broadening
- Determine the physical mechanism and source region of beat wave modulation by changing the frequency of high-frequency waves