Majorana zero modes,unconventional real–complex transition,and mobility edges in a one-dimensional non-Hermitian quasi-periodic lattice

Shujie Cheng(成書杰) and Xianlong Gao(高先龍)

Department of Physics,Zhejiang Normal University,Jinhua 321004,China

Keywords: non-Hermiticity,Majorana zero mode,mobility edge,unconventional real-complex transition

1. Introduction

In 1958,P.W.Anderson uncovered that the absence of the diffusion of wave packets can be induced by disorder.[1]Since then, Anderson localization has gradually appealed much attention and becomes an active research area in condensedmatter physics. The scaling theory tells us that when the strength of the disorder reaches the threshold, all the eigenstates of the one-dimensional(1D)and two-dimensional(2D)systems will be the Anderson localized states. However,Mott found that in some exceptional systems, i.e., the threedimensional(3D)Anderson model,only part of the eigenstates are localized,which are separated from the extended states by the so-called mobility edges.[2]

In reality, beyond the 3D systems, in the 1D quasiperiodic systems, known as the Aubry-Andr′e-like (AA-like)models (extensions of AA model[3]), there also occur mobility edges(MEs). Here, the quasi-periodicity accounts for the uncorrelated disorder. In 1988,Sarmaet al. discovered that in a class of AA-like model with slow-varying potentials, there also exist MEs.[4]The numerical solutions show that the density of states peaks at MEs, and the first-order derivative of the Lyapunov exponent is discontinuous at MEs. Later, an asymptotic semiclassical technique was proposed to locate the MEs.[5]The authors transformed the problem of solving the mobility edge into the problem of analyzing the solution of a characteristic equation. The complex solutions correspond to the extended states, and the real solutions correspond to the localized states. Accordingly,mobility edges are acquired by this strategy. Recently, this analytical method is developed to calculate the MEs in off-diagonal AA-like models.When the slow-varying potential is incommensurate and the hopping amplitudes are commensurate, Liuet al. found that there are two pairs of MEs at weak potential strength,and the system becomes Anderson localized when the potential gets stronger.[6]When the off-diagonal term is incommensurate and the potential is commensurate, there is a pair of parallel MEs;when the two terms are both incommensurate,there will appear multiple MEs,and the singularity at which the MEs intersect signals the Anderson localization.[7]Furthermore,Liuet al. investigated the delocalization-localization properties of another form of off-diagonal AA-like model.[8]The results show that the wave functions present multifractal behavior,thus making the phase diagram consist of extended phase and critically localized phase. Recently, this theoretically model has been experimentally realized by taking advantage of ultracold atomic momentum-lattice engineering and these phases predicted in Ref. [8] were successfully probed by observing the dynamical inverse participation ratio(IPR).[9]

Decade ago, ME was discovered in a AA-like model with long-range hoppings by Biddleet al.[10]In that paper, they solved the expression of the ME by the dual transformation. The exact ME is coincident with the energy spectra embellished by the IPR. In 2015, Ganeshan investigated the delocalization-localization properties of an AAlike model with generalized potentials.[11]They demonstrated the presence of the MEs in this model by means of the dual transformation. The analytical ME accurately partitioned the energy spectrum into the extended and the localized parts. For this model, Xuet al. carried out some dynamical investigations.[12]The dynamical behaviors, such as the wave packet propagation and Loschmidt echo in the intermediate regime where the mobility edge appears are in contrast to those in the extended and localized regimes. Particularly, Wanget al. discovered the duality between two typical AA-like models[13]and invariable MEs were discussed in Ref. [14]. Besides, MEs have been investigated in other quasiperiodic models with self-dual symmetry.[15-17]

Non-Hermiticity always brings about some novel quantum phenomena without any analogy to the Hermitian case, such asPT-symmetry breaking,[18-20]exceptional points,[21-26]anomalous bulk-boundary correspondence,[27]and non-Hermitian skin effect.[28-33]Furthermore, the interplay between the uncorrelated disorder and non-Hermiticity will give rise to the delocalization-localization transition.[34-41]An intriguing discovery is the appearance of MEs in Hanato-Nelson model with nonreciprocal hoppings.[42-45]A recent study provides an intuitive topological explanation why localization transition happens in the Hatano-Nelson model.[46]Not only that, MEs appear in the non-Hermtian systems accompanied by the quasi-periodic potentials,showing their robustness against the uncorrelated disorder and non-Hermiticity. For example, Liuet al. concentrated on the relationship between the Anderson localization and thePT-symmetry breaking as well as the MEs in a 1D non-Hermitian quasicrystal.[47]The main findings are that Anderson localization is accompanied by thePT-symmetry breaking,and MEs only emerge in the real energy part. Zenget al. determined the topological nature of MEs in a non-Hermitian AA-like model.[48]Liuet al. studied two general AA-like models with non-Hermitian potentials, and acquired exact MEs by means of the self-dual condition.[49]In experiments,MEs were successfully observed in 3D Anderson models[50-52]and 1D AA-like models.[53-56]

The delocalization-localization transition and topological superconducting were originally two different research fields, but now are linked by the p-wave pairings. Kitaev model[57]is a standard superconducting model to interpret the topological transition in topological superconductors. The AA-like model with p-wave pairings can be viewed as the quasi-periodic generalizations[58]of the Kitaev model,implying that both the two mentioned phenomena are capable of occurring in a topological superconductor. Coincidently, the phenomenon that the Anderson localization transition is synchronized with topological superconducting transition was uncovered by Caiet al.[58]Almost at the same time, the transport properties of this quasi-periodic topological superconductor were well discussed.[59]However, the exploration of the physics behind such types of systems is far from over. Recently, the extended-critical was detailedly discussed in the topological non-trivial phase with chirally distributed Majorana zero states. Moreover, the extended and critical regions as well as their boundaries completely accord with the predictions by the multifractal analysis.[60]In recent years, the relevant studies have been extended to other quasi-periodic generations,[61-65]and besides, the quench dynamics[66]and Kibble-Zurek machanism[67]were well investigated.

It was noted that the topological non-trivial region of the Kitaev model where Majorana zero mode (MZM) exists is independent of the superconducting pairing strength, and is only determined by the hopping amplitude.[57]The quasiperiodic potential unexpectedly becomes an advantage that it broadens the original topological non-trivial region,[58]offering multiple degrees of freedom to manipulate the topological superconducting transition. Dramatically, this advantage brought by quai-periodicity is greatly fragile in the presence of non-Hermiticity, which will compress the original non-trivial region.[68]But at least, we should reach an agreement that MZMs dot not disappear in spite of non-Hermiticity.[68-74]In addition, we know that the non-Hermitian systems usually have complex eigenvalues,which are the direct results of nonconservation of probability on account of gain and loss. However, Bender and Boettcher found that in a class of systems withPT-symmetry(combination of parity(P)symmetry and time-reversal(T)symmetry),there exist pure real energies.[18]The reason why there exists real energies is that thePTsymmetry allows the gain and loss to be coherently balanced.PT-symmetry breaking indicates that such a balance is broken, then the energies become complex. For decades, thePT-symmetry was once regarded as the minimum constraint to preserve the real energies. The latest researches, however, have shattered that perception. There exists a type of unconventional real-complex transition independent ofPTsymmetry breaking. Hamazakiet al.found that in a non-Hermitian many-body system with only time-reversal symmetry, many-body localization can significantly restrain the imaginary part of the complex energies,whereas a system with broken time-reversal symmetry cannot retain real energies.[75]Hereto, does this result mean that the time-reversal symmetry is the lowest constraint to maintain real energies? The answer is negative. Reference[68]showed that in a class of non-Hermitian topological superconductor only with particle-hole symmetry, the real-complex transition still exists. Moreover,different from the consequence of Hamazakiet al., here the extended phase maintains the real energies.

In reality, a topological superconductor cannot avoid the exchange of matter and energy with its surroundings, forming the so called non-Hermitian systems, and this exchange is not conductive to the existence of MZM.[68]Therefore, it is desirable to search a topological superconductor that is robust against the non-Hermitian perturbations. In this paper,we are motivated to theoretically engineer a topological superconductor which is capable of preserving the same topological features as their original Hermitian case,and thus immune to the fragility caused by the non-Hermitian perturbations. A topological phase diagram will be presented by means of the transfer matrix method and the relationship between the topological phase transition and the gap closing will be discussed.Besides, we will analyze its energy spectrum to find if there will be a unconventional real-complex transition independent ofPT-symmetry breaking. Furthermore, we try to reveal the correspondence between the real-complex transition and delocalization-localization transition in this system and verify this correspondence by means of the IPR.

The rest of this paper is organized as follows. Section 2 describes the non-Hermitian p-wave superconductor and presents its Hamiltonian both under periodic boundary condition (PBC) and open boundary condition (OBC). Section 3 introduces the transfer matrix method on the purpose of extracting theZ2topological invariant of this system. Section 4 contains the analysis of the MZMs, the topological phase diagram, and the real-complex transition, as well as the correspondence between real-complex transition and the delocalization-localization transition by means of the IPR.Section 5 summarizes the results of these investigations.

2. Model and Hamiltonian

We consider a one-dimensional p-wave superconductor with generalized non-Hermitian quasiperiodic on-site potentials,whose Hamiltonian in the real space is expressed as

wherenis the site index,Lis the size of the system, and ?cn(?c?n) is the fermion annihilation (creation) operator.tin the hopping amplitude chosen as the unit of energy, andΔdenotes the strength of superconducting pairings between the nearest-neighbor sites.[57]We choose the realΔwhich makes it clear that our system does not possessPT-symmetry,[18]and the system belongs to the class D in the topological classification.[76]The generalized non-Hermitian potentialVnhas the following form:

Due to the particle-hole symmetry, we can make a diagonalization on the Hamiltonian in Eq. (1) to obtain its energy spectrum.We perform the Bogoliubov-de Gennes(BdG)transformation

Definitely,His a 2L×2Lmatrix.By diagonalizingH,we can acquire the full energy spectrumEjand the corresponding wave functions|ψj〉directly.

In the next section,we will discuss the topological properties of the system,such as theZ2topological invariant,Majorana zero energy modes,and the corresponding states. Moreover, we will quantitatively analyze the real-complex energy transition and the mobility edge by the inverse participation ratio.

3. Transfer matrix method

As mentioned that our system belongs to the class D in the topological classification,the topological properties of the system are directly reflected by aZ2topological invariantM.We determineMby the scattering matrix method,[77,78]for the reason that this method is well-behaved in non-Hermitian topological superconductor.[68]The scattering matrixSconsists of four submatrices with the following form:

where sgn is the sign of the determinant (Det) ofR. WhenM=-1, the system is in the topological nontrivial phase,which supports the existence of the Majorana zero-energy mode(MZM),andM=1 corresponds to the topological trivial phase where there is no any MZM.

The scattering matrixScan be acquired by the transfer matrix scheme.We set the Fermi energy atEF=0,then Eq.(4)with zero energy is rewritten as

In order to separate the left-moving and right-moving waves,we need to introduce a unitary operatorsU. After performing a unitary transformation, the total transfer matrix becomes[68,77,78]

Therefore, we can calculate the total transfer matrixλto obtain theZ2topological invariantM.

4. Results and discussion

At the beginning, we investigate the topological properties of this system. For convenience but not losing generality,we takeΔ=0.5tthroughout the following studies. Along the above strategy, we numerically calculate theZ2topological invariantMwith various potential strengthVand finally acquire the phase diagram,which is explicitly shown in Fig.1.Intuitively, there are two different phases withM=-1 andM=1, respectively. According to Ref. [68], we know that hereM=-1 stands for the topological non-trivial phase andM=1 denotes the topological trivial phase. Forb=0, we have already known that our model is reduced to the Kitaev model,whose topological boundary isV=2t.For other differentb,the topological boundary is also stably located at aboutV=2t, reflecting that the topological properties are immune to the non-Hermtian disturbance. This feature is of importance to its practical applications. Moreover,we note that the topological boundary is the same as that of the Kitaev model.From this aspect,our theoretical model is the reappearance of the Kitaev model in the non-Hermtian case.

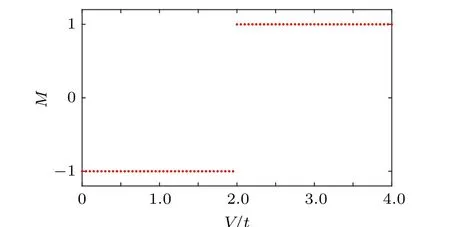
Fig.1. The Z2 topological invariant M as a function of the potential strength V.M=-1corresponds tothe topologicalnon-trivial phase,a√nd M=1 denotes the topologicaltrivial phase.Otherparameters areα=(5-1)/2 and Δ =0.5t.

For topological insulators and Chern insulators,gap closing is a key feature to manifest the topological phase transition. We find that this characteristic is not an exception in our non-Hermitian p-wave superconductor. With the purpose of making this conception explicit,we investigate how the real gapΔrgbehaves with potential strengthV.Δrgis the difference of the(L+1)-th real energy level and theL-th real energy level under PBC with the definition ofΔrg=EL+1-EL. We choose four typical values of parameterb(b=0.1,0.4,0.7,and 0.9)and fix the size of the systemL=500, then the corresponding energies can be extracted by diagonalizing the matrix presented in Eq. (6). Figure 2 shows the variation ofΔrgas a function of the potential strengthVwith variousb. For differentb, the real gap of this system is readily seen to be closed atV=2t. What needs illustration is that for larger size of the system,the gap closing point still locates atV=2t.This result is in accordance with the phase diagram in Fig.1,and confirms the prediction that the topological superconducting transition is accompanied by the gap closing. Recalling the potential defined in Eq. (2), in fact, we expanded it as the superposition of the homogeneous Hermitian part and the non-Hermitian quasiperiodic one which consists of terms with various orders of the parameterb. When the potential strength is small,the energy gap is sensitive to the non-Hermitian quasiperiodic terms.Accordingly,we can see that in Fig.2,when the system is in the topological phase,the gap changes as the parameterbvaries. When the potential strength becomes large,the energy gap will be dominated by the homogeneous Hermitian part.Therefore,from Fig.2,we can see that in the topological trivial phase, the energy gap curves for differentbcollapse to a single line.

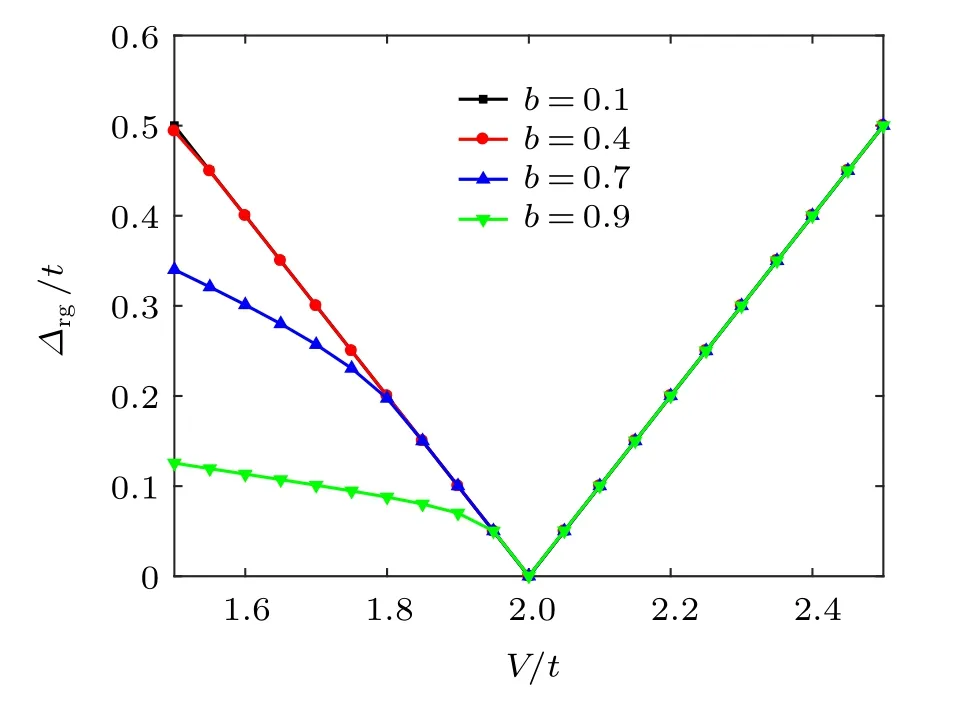
Fig.2. The variation ofrealenergy gap√Δrg asa functionofV withvarious b. Otherinvolved parametersare α =(-1)/2,Δ =0.5t,andL=500.

Now that we have figured out the topological phases of the system, what other physical information can be extracted from the topological non-trivial phase? By considering OBC,b=0.5,andL=500,we acquire the real part of excited spectrum of the superconductor,shown in Fig.3(a). As the picture shows, there are MZMs in the topological non-trivial phase(V<2t), while the MZM in the trivial phase (V>2t) is absent. In other words, MZM is protected by the topology. We further want to investigate the bulk-edge correspondence by analyzing the lowest excitation mode. With this purpose, we rewrite the BdG operator in Eq.(4)as

Figures 3(b) and 3(d) (3(c) and 3(e)) present spatial distributions of|φ|(|ψ|)for their corresponding lowest excitation modes. According to the real excitation spectrum, we immediately know that whenV=1.5t, the lowest excitation mode is exactly the MZM. It can be seen that|φ| and|ψ| are distributed at the disparate ends of the superconductor,implying that the original paired Majorana fermions (MFs) have been split into two independent and spatial-separated MFs. This phenomenon is the direct result of non-trivial topology. Moreover, no anomalous edge state[27]is found here. In the same way,we know that whenV=2.5t,the lowest excitation mode ceases to be the MZM, but corresponds to the bulk state. As Figs.3(d)and 3(e)show,|φ|and|ψ|are distributed in the bulk of the system,signifying that there is no spatial-separated MF.This circumstance is determined by the trivial topology.

Fig.3.(a)The real part of excitation spectrum under OBC.The MZM exists when V <2t. Spatial distributions of|φ|and|ψ|for the lowest excitations with V =1.5t in(b)and(c),respectively,and with V =2.5t in(d)and(e),respectively. V =2t is the topological phase transition point of the system.Other involved parameters are b=0.5,α =(5-1)/2,and L=500.

For non-Hermitian systems, we intuitively take the attitude that their eigenvalues are complex. Nevertheless,the theorem proposed by Bender and Boettcher points out that there are real energies in systems withPT-symmetry.[18]When this symmetry is broken, then the energies become complex. Recently,there was a research that discovered an unconventional real-complex energy transition independent ofPT-symmetry breaking.[68]This intriguing finding motivates us to make it clear if there is other types of real-complex transition that is not dominated byPT-symmetry breaking. For the sake of general consideration,we takeb=0.5,L=2000,and OBC in the following analysis. Figure 4(a)plots the energy spectrum in the complex plane withV=0.2t. The system now is in the topological non-trivial phase. Intuitively, the imaginary parts of the energies are suppressed at Im(E)=0. We conjecture that the real energies are closely related to the extended states.To validate this speculation,we introduce the IPR,

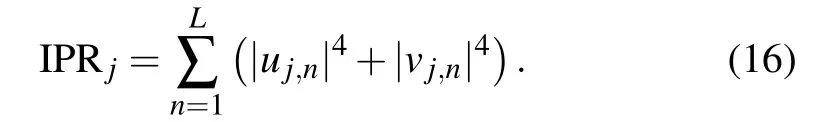
For a normalized wave function, if its IPR scales as IPRj∝1/L(approaching 0 at largeL),then this wave function is extended; if IPR is greater than zero (approaching 1), then this wave function is localized.[79]Figure 4(b)shows the variations of IPR with Re(E) atV= 0.2t. With large system size, it is readily seen that IPRs are approaching zero, implying all these wave functions are extended. Figures 4(c) and 4(d) are the probability distributions of the typical extended wave functions taken from the 71-th and 1921-th excitation modes, respectively. Readily,the wave functions extend throughout the system, conform to the analysis by the IPR. Here,pdenotes the probability,satisfyingpn=u2n+v2n,and the same below.

Fig.4.(a)Energy spectrum in the complex plane with V =0.2t.(b)IPR versus Re(E). Panels (c) and (d)show typical extended wave functions taken from the 71-th and 1921-th excitation modes, respectively. Other involved parameters are α =(5-1)/2 and L=2000.

If we takeV=6tand the system is in the topological trivial phase, then we will observe distinctly different phenomena. Compared to the energy spectrum in Fig. 4(a), the energies atV=6tshown in Fig.5(a)are fully complex. The spectrum presents a closed loop, indicating that there is no skin effect.[30,31]We plot the IPR as a function of Re(E) in Fig. 5(b). As the figure shows, IPRs are finite numbers, approaching 1, which indicate that these wave functions are localized. We choose two typical localized wave functions as two intuitive examples. Figures 5(c) (the 520-th excitation mode) and 5(d) (the 578-th excitation mode) show that the wave functions are localized in the bulk of the system.

Fig. 5. (a) Energy spectrum in the complex plane with V =6t. (b) IPR versus Re(E). Panels(c)and(d)are the possibility distributions of typical localized wave functions taken from the 520-th and 578-th excitation modes,respectively. Other involved parameters are α =(5-1)/2 and L=2000.

From the above numerical analysis, we construct such a correspondence that real energies correspond to the extended states and complex energies to the localized ones. Motivated by this correspondence, we wander whether there exists another type of real-complex transition, i.e., when the parameters are specified, the energies consist of pure real part and complex part. The reason why we pay attention to this issue is that this case will lead to the appearance of MEs. To reveal its existence,we takeV=1.5t. According to the topological phase diagram in Fig.1,we know that the topological invariant isM=-1,implying that the system is in the topological nontrivial phase.Accordingly,there appears MZM(see Fig.3(a)),whose spatial distributions are shown in Figs.3(b)and 3(c),respectively. However,in this case,the spectrum in the complex plane presents different features. Concrete speaking,the spectrum consists of two small loops and two big loops,as well as two regions of real energy(see Fig.6(a)). Besides,the IPRs of the loop regions are finite numbers,larger than zero,whereas the ones of the real-energy regions are zero(see Fig.6(b)). In Fig. 6(c), the red line shows the probability distribution of a typical localized wave function taken from the 10-th excitation mode whose corresponding energy is located at the small energy loop and the green line denotes the one taken from the 1990-th excitation mode whose corresponding energy is located at the big energy loop. Differently, in Fig. 6(d), we see a extended probability distribution whose corresponding wave function is taken from the 578-th excitation mode with pure real energy. The difference of the characteristics of the wave functions announces that the presence of the ME. Intuitively seen from Fig.6(a),these two types of correspondences are separated by four magenta dashed lines,i.e.,the so called MEs.

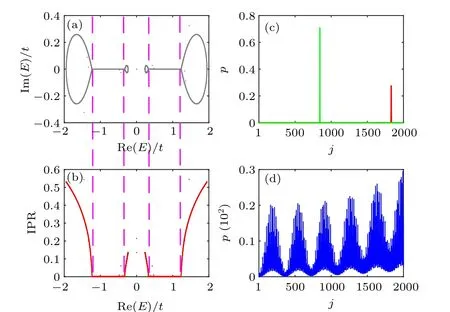
Fig. 6. (a) Energy spectrum in the complex plane with V =1.5t. (b) IPR versus Re(E). The magenta dashed lines denote the MEs. (c)Red line denotes the probability distribution of a typical localized wave function taken from the 10-th excitation mode whose corresponding energy is located at the small energy loop and green denotes the one taken from the 1990-th excitation mode whose corresponding energy is located at the big energy loop.(d)Probability distribution of a typical extended wave function taken from the 578-th excitation mode with pure real energy.Other involved parameters are α =(5-1)/2 and L=2000.

The reason why the small energy loop forms the localized states can be understood as the competition between the extended p-wave pairing and the localized quasi-disorder. As mentioned before, the potential consists of the homogeneous part and the non-Hermitian quasiperiodic part. AtV=1.5t,for the low-energy excitation states,the quasiperiodicity dominates, making these be localized. AsVincreases, reaching a finite strength,such asV=2.5,the extended homogeneous potential dominates, making the low-energy excitation states be extended. As Fig.7 shows, the spectrum atV=2.5tconsists of two loop regions and two real energy regions, separated by a pair of MEs. The transition of energy from complex to real appropriately describes the transition of the wave functions from the localized to extended ones by the IPR.The separation lines (magenta dashed lines) are numerical MEs. As two intuitively physical pictures,Fig.7(c)shows the probability distribution of a typical extended wave function taken from the 50-th excitation mode with pure real energy and Fig.7(d)shows the probability distribution of a typical localized wave function taken from the 1950-th excitation mode with complex energy.

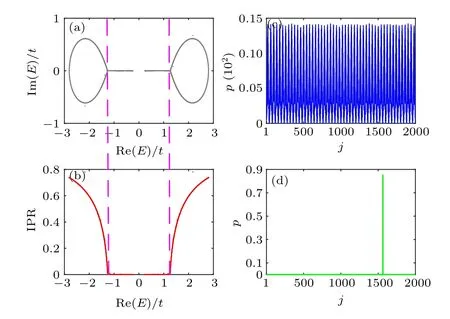
Fig. 7. (a) Energy spectrum in the complex plane with V =2.5t. (b) IPR versus Re(E).The magenta dashed lines denote the MEs.(c)Possibility distribution of a typical extended wave function taken from the 50-th excitation mode with pure real energy.(d)Possibility distribution of a typical localized wave function taken from the 1950-th excitation mode with complex energy.Other involved parameters are α =(-1)/2 and L=2000.

5. Summary

All in all, we have investigated the topological properties,energy spectrum features,and delocalization-localization properties of a general non-Hermitian p-wave superconductor. We have known that the system is robust against the non-Hermitian perturbations and preserves the same topological boundary as the original Kitaev model. By calculating the IPR, we have successfully contributed a general correspondence that real energies correspond to the extended states and the complex ones correspond to the localized states. This correspondence will be instructive to detect the unconventional real-complex transition and delocalization-localization transition in other non-Hermitian systems. Our work directly connects three hot research areas: topological superconductors,real-complex transition induced by non-Hermiticity, and Anderson localization, and will promote comprehensive development of these areas. Unfortunately, it is unknown whether there exists a type of symmetry breaking which results in this unconventional real-complex transition. Therefore, revealing the origination of this unconventional real-complex transition remains an open question.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant Nos.11835011 and 12174346).