Boundary states for entanglement robustness under dephasing and bit flip channels*
Hong-Mei Li(李紅梅), Miao-Di Guo(郭苗迪), Rui Zhang(張銳), and Xue-Mei Su(蘇雪梅)
College of Physics,Jilin University,Changchun 130012,China
Keywords:entanglement,decoherence,robustness,local unitary equivalence
1.Introduction
Quantum entanglement is one of the most intriguing features of quantum mechanics.[1,2]It is a major resource for quantum information processing(QIP),such as quantum computation,[3,4]quantum teleportation,[5,6]quantum key distribution,[7–9]and distributed quantum learning.[10]Recently, much attention has been paid to the unavoidable degradation of entanglement due to decoherence in realistic environment.[11–13]The entanglement of a bipartite quantum system can decay to zero abruptly under the effect of local environment,which is a well-known decoherence phenomena named as entanglement sudden death(ESD).[14–17]It was shown that the ESD is related to the type of initial state.[18,19]
There are many excellent papers have been devoted to the study of the robustness of various bipartite[20,21]and multipartite entangled states under different decoherence models.[22–26]It is possible to calculate the exact value of the geometric measure of entanglement for special states under collective dephasing.[22]In addition,the robustness of entanglement for some highly entangled multiqubit pure states against various decoherence is obtained.[23]To make a thorough understanding about the robustness of a specific state,it is useful to compare it with random states.[24]For a two-qubit system under decoherence,[20]we find that the Bell-like states are always the most robust ones;for the three-qubit system,[27]we investigated the entanglement robustness under amplitude damping,dephasing and bit flip channels,respectively,and found the most robust genuine tripartite entangled states and the most fragile ones.
The entanglement robustness for the case of n-qubit states has been extensively analyzed.[23,28,29]By studying the disentanglement dynamics of the generalized N-qubit GHZ states under the amplitude-damping channel,some authors affirm that the entanglement robustness can be enhanced by local unitary(LU)operations though the amount of entanglement itself cannot.[28]However,they did not discuss to what extent the robustness of entanglement can be enhanced.It is of theoretical interest and has potential application in accomplishing some quantum task.
In this paper,we investigate the robustness of n-qubit states under the dephasing and the bit flip channels. Negativity corresponding to the partitions“the first qubit versus the rest”will be used as the entanglement quantifier. We show how the entanglement evolution of two forms of special states,which are local-unitarily equivalent to each other and therefore possess precisely the same amount and type of entanglement in absence of decoherence,is influenced by the number of qubits n.We also find that the two forms of states exhibit the most significant different robustness by comparing with random states,which further confirm the important fact that the entanglement robustness of an n-qubit system can be greatly enhanced by LU operations.
The paper is organized as follows.In Section 2 we briefly introduce our environment models and entanglement measure for some special multiqubit systems.In Sections 3 and 4 we investigate the robustness of entanglement under the dephasing and the bit flip channels,respectively.Finally,we summarize our conclusions in Section 5.
2.Noise models and entanglement measure
We consider a multi-qubit system interacting with dephasing and bit flip channels,respectively. We assume that each qubit in the composite system is coupled to its own noisy environment and there is no interaction between qubits.That is,all qubits are affected by the same decoherence process.The dynamics of a single qubit is governed by a master equation that gives rise to a completely positive trace-preserving map(or channel)ε describing the corresponding evolution:[23]ρi(t)=ε(t)ρi(0).In the Born–Markovian approximation,the channel can be described by a set of Kraus operators[23,30,31]as
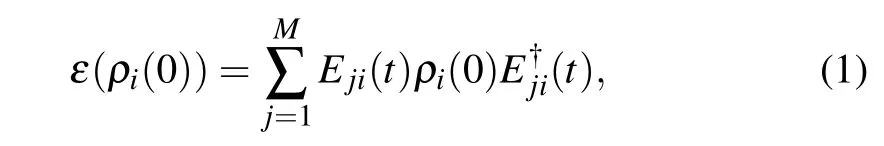
where Ej(t)(j=1,...,M)are the Kraus operators needed to completely characterize the channel which fulfill the normalization condition
We start by discussing the dephasing channel,which can be also regarded as a phase flip channel.It describes the loss of quantum coherence without any exchange of energy.The Kraus operators for the dephasing channel are
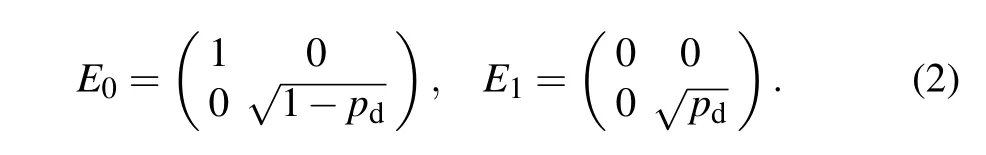
Another type of environment to be dealt with is bit flip channel.The corresponding Kraus operators can be given by
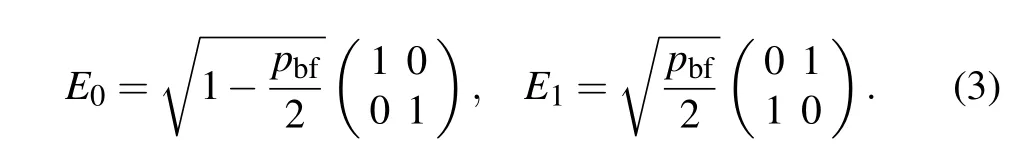
The parameter pd,pbfin channels(2)and(3)can also be interpreted as the degree of decoherence of an individual particle in multiqubit system with pd,pbf∈[0,1],where pd,pbf=0 means no decoherence and pd,pbf=1 complete decoherence.The factor of 2 in Eq.(3)guarantees that at pbf=1 the ignorance about the occurrence of an error is maximal,and as a consequence,the information about the state is minimal.[30]
To examine the bipartite entanglement dynamics for nqubit states,we use negativity[32–34]as the measure of entanglement between the first qubit q1and the rest ones Qn?1(hereafter denoted by.Negativity is extensively used in study of the multipartite entanglement dynamics,though it cannot detect the positive partial transpose(PPT)entangled states.Based on the trace normof the partially transposed density matrix ρTA of a mixed state ρ,the entanglement can be written as[34,35]
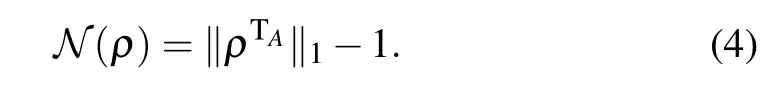
The trace norm of any Hermitian operator A iswhich is equal to the sum of the absolute values of the eigenvalues of A.The partial transpose density matrix has negative eigenvaluesμi<0 and positive eigenvaluesμj>0,it satisfiesthus its trace norm reads in generalTherefore,the negativityis defined as twice the absolute value of the sum of the negative eigenvalues of
3.Robustness of entanglement under dephasing channel
3.1.Evolution of special states under dephasing channel
The dephasing channel reflects the decay of non-diagonal elements of density matrix with time.In this channel,we focus first on the n-qubit system in the form of pure states

where θ ∈[0,π/2].ik,jk=0,1 and k=2,3,...,n with odd numbers of{ik}and even numbers of{jk}taking 1,respectively.means all possible permutations of{ik}and{jk}.The initial entanglement of the above states(5)can be simply derived as=sin2θ.
In the following,we take the example of a four-qubit system in the pure stateto calculate its negativity under the dephasing channel.We note that the negativity of the states(5)with n=4 is determined by the partial transposed density matrix.The nonzero diagonal matrix elements ofare given by
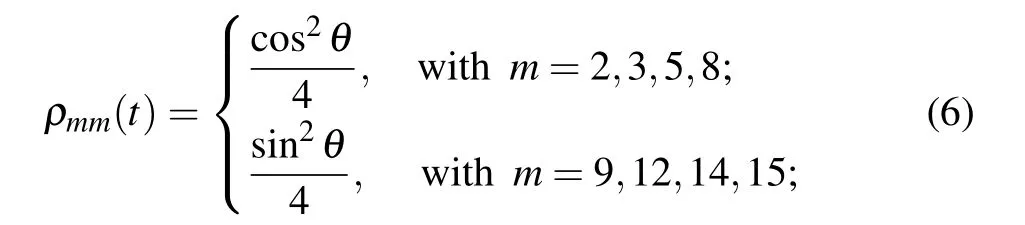
and the nonzero off-diagonal terms are given by

with m=1,4,6,7,n=10,11,13,16,and n17?m;and
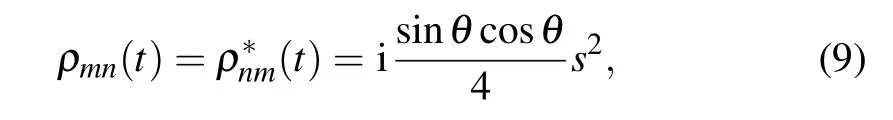
with m=1,4,6,7,n=17 ?m.Hereafter,s1 ?pd(or pbf)in the partially transposed density matrix.
The negativity corresponding to the bipartitionfor the statecan be readily calculated as
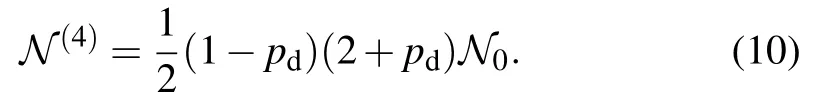
Similarly,the negativities for the stateswith n=2,3,5,6,and 7 are given by
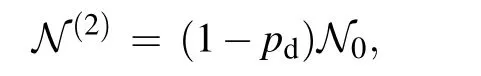
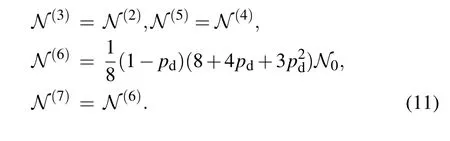
From Eq.(11),with the same N0,the entanglement for the statesin Eq.(5)does not decrease with n,namely,
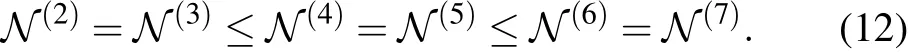
In other words,the entanglement ofdoes not become more fragile when the size of system increases.
Next,we discuss the other form of pure states for an arbitrary n-qubit system
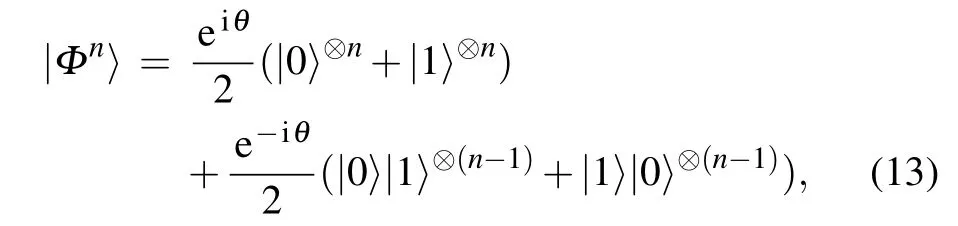
where θ ∈[0,π/2].These states are related to the statesby an LU transformation as

with
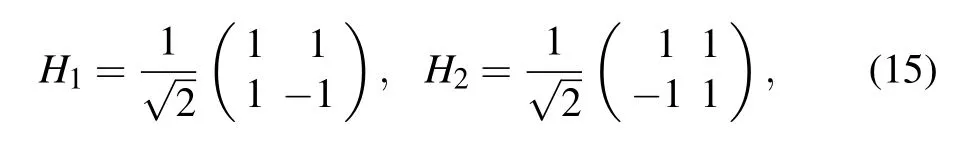
which are both the Hadamard matrices. That is,are LU-equivalent toTherefore,these two special forms of states possess precisely the same amount and type of entanglement in absence of decoherence.Specifically,the bipartite entanglement of the initial states(13)can also be expressed as=sin2θ.
The partial transposed density matrixunder the dephasing channel is given by

here h.c.represents the hermitian conjugate of the previous terms.The matrix has only one negative eigenvalue which is determined by the following 4×4 matrix:
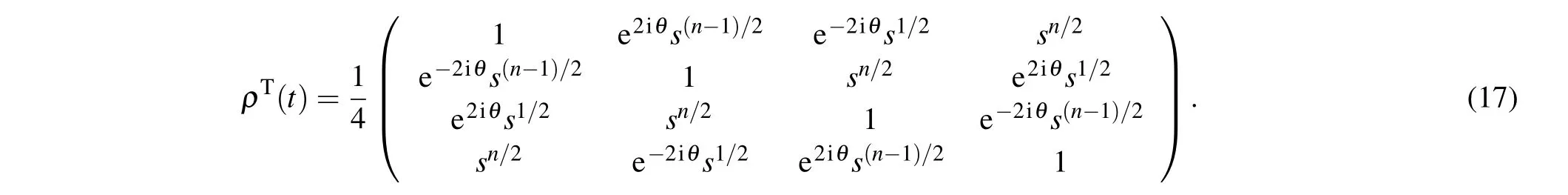
The negativities corresponding to the bipartitionfor the states in Eq.(13)can be expressed as
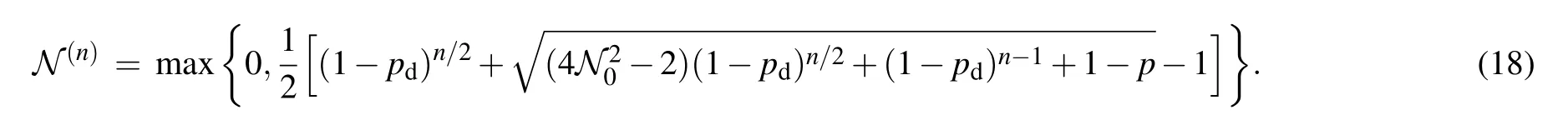

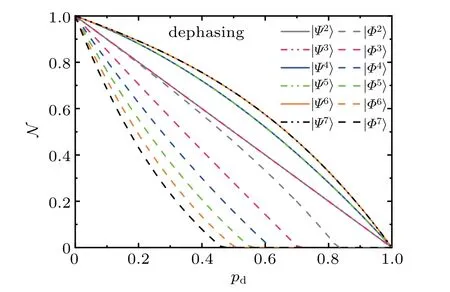
Fig.1. Negativities of bipartition q1|Qn?1,as a function of pd,for the states(solid lines or dashed dot dot lines)and(dashed lines)with θ=π/4 under the local dephasing.The systems with n=2,3,...,7 are shown with gray,pink,blue,green,orange,black curves,respectively.
3.2.Robustness of multiqubit pure states under the dephasing channel
In our previous work,[27]we found that the statein Eq.(5)is the most robust entangled state,and the statein Eq.(13)is the most fragile entangled one under the dephasing channel. Now,we turn to the decoherence process of all nqubit pure states under the dephasing channel with numerical calculation.The remaining negativity N of a state which is affected by the fixed decoherence noise is used as the quantifier of robustness.By taking a four-qubit system as an example,we sample 3×104random four-qubit entangled pure states with the Haar measure[36]and compute their remaining entanglements with pdtaking the values 1/8,2/8,3/8,and 4/8,respectively.The corresponding remaining negativitiesare plotted in Figs.2(a)–2(d)with gray solid dots.In addition,according to Eq.(10)and Eq.(18),one can easily get the relation betweenandwith the same values of pdcorresponding to the statein Eq.(5)and the statein Eq.(13).In Figs.2(a)–2(d),the remaining negativities are depicted with red solid lines for stateand olive dashed lines for state
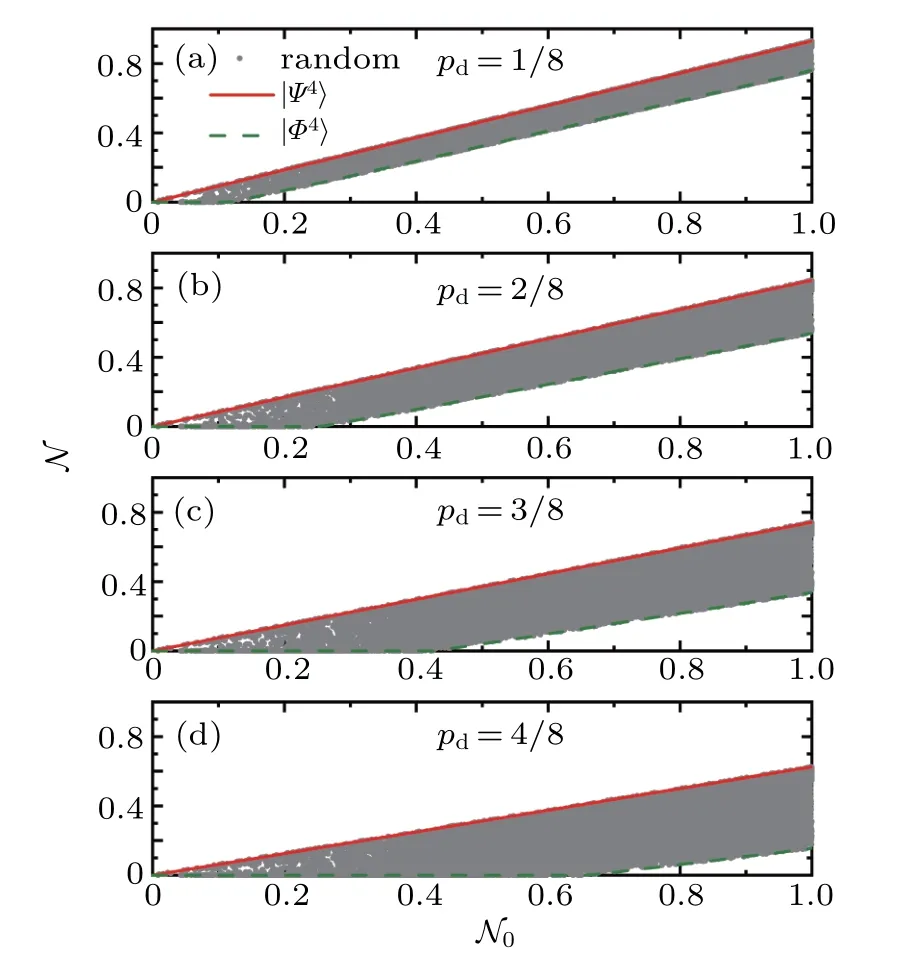
Fig.2.The remaining negativities versus the initial entanglement for a four-qubit system in the 3×104 random sampled pure states(gray solid dots),special states(red solid lines)and(olive dashed lines)under the dephasing channel.We plot the remaining negativities characterizing robustness of the state when the dephasing noise pd=1/8,2/8,3/8,and 4/8 in panels(a),(b),(c),and(d),respectively.The same behavior is displayed for all other noise parameters and for systems with n=2,3,5,6,and 7.
In Fig.2,the remaining negativitiesof 3×104random four-qubit pure states display ribbon distributions.The red solid lines are the upper bounds;while the olive dashed lines are the lower bounds.In other words,stateis the most robust entangled state,while stateis the most fragile one for the four-qubit system during decoherence under the dephasing channel,although they are LU-equivalent with each other.The results imply that the suitable LU operations can enhance the robustness of entanglement to the max.We also explored the dephasing process of another multiqubit pure state with n=2,5,6,and 7,and obtain the same result.Therefore,we suppose that the conclusion is universal for n-qubit entanglement corresponding to the bipartition
4.Robustness of entanglement under bit flip channel
4.1.Evolution of special states under bit flip channel
The bit flip channel is the same as the dephasing channel under the local rotational transformation.It flips the state of a qubit betweenandwith a certain probability and each qubit is affected by the noise correspondingly.The statesin Eq.(13)andin Eq.(5),which can be transformed into each other by local operations and manifest the most significant difference in robustness under the dephasing channel,are worth to be investigated further for this channel. Similarly,we also take the example of the pure statesandto calculate the negativities under the bit flip channel.We need to write the nonzero elements of the partial transposed density matrixandduring the evolution,which are given in Appendix A.Here the negativities expressions ofwith n=2,3,...,7,are straightforwardly provided as follows:
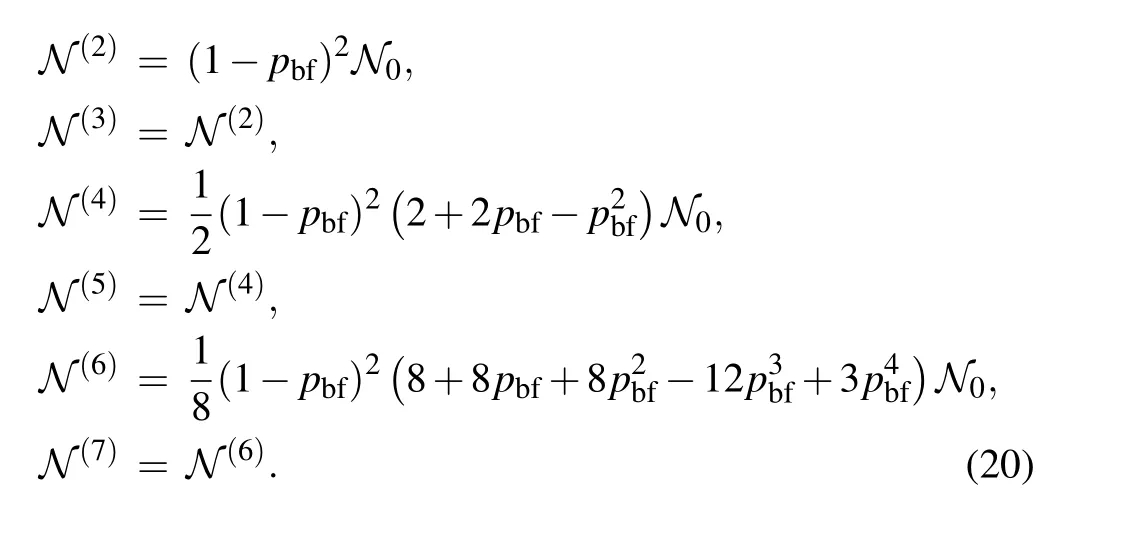
The negativities between the bipartitionfor the statesunder the bit flip channel are given by
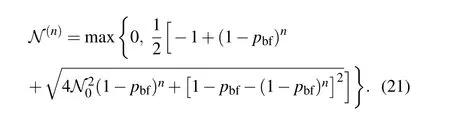
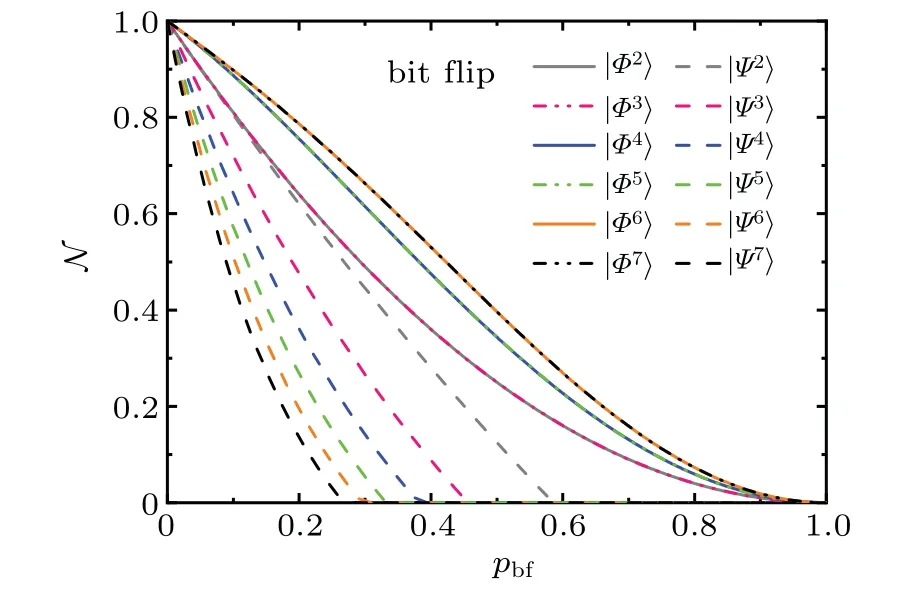
Fig.3.Negativities of bipartition q1|Qn?1,as a function of pbf,for the states|(solid lines or dashed dot dot lines)and(dashed lines)with θ=π/4 under the bit flip channel.The systems with n=2,3,...,7 are shown with gray,pink,blue,green,orange,black curves,respectively.
4.2.Robustness of multiqubit pure states under the bit flip channel
The decoherence process of all multiqubit pure states under the bit flip channel is also explored similar to the case of the dephasing channel.We plot the remaining negativities N for the statein Eq.(13),the statein Eq.(5),and random sampled states when the degree of bit flip pbf=1/8,2/8,3/8,and 4/8 with olive dashed lines,red solid lines,and gray solid dots in Figs.4(a)–4(d),respectively.
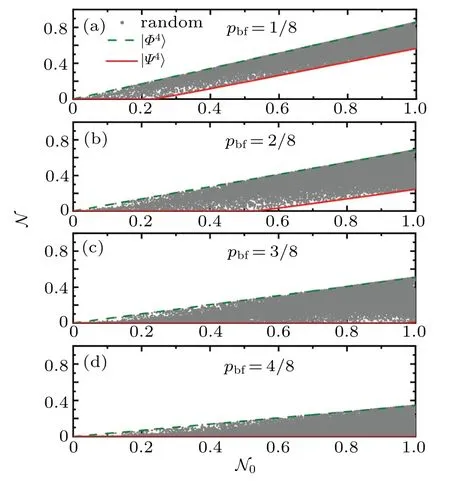
Fig.4.The remaining negativities versus the initial entanglement for a four-qubit system in the 3×104 random sampled pure states(gray solid dots),special states(red solid lines)and(olive dashed lines)under the bit flip channel. We plot the remaining negativities characterizing robustness of the state when the bit flip noise pbf=1/8,2/8,3/8,and 4/8 in panels(a),(b),(c),and(d),respectively.The same behavior is displayed for all other noise parameters and for systems with n=2,3,5,6,and 7.
From the figure,one can see that there is a ribbon distribution forof 3×104random four-qubit pure states.Since the same unitary operation also connects the bit flip channel with the dephasing channel,the stateis the most robust entangled state,while the stateis the most fragile one under the bit flip channel.For the cases of n=2,3,5,6,7,we have the same results. We suppose that the conclusion is universal for n-qubit entanglement corresponding to the bipartition
5.Conclusion
In summary,we have investigated the robustness of entanglement for a multiqubit system under the dephasing and the bit flip channels.We explore the entanglement evolutions of two forms of special n-qubit statesandwhich are LU-equivalent to each other and therefore posses precisely the same amount and type of entanglement.For the dephasing channel,with n=2,3,...,7,the robustness of the statesdoes not decrease with n,while for the statesthe robustness does not increase with the size of system.The larger number of qubits a system has,the greater distinction the entanglement evolution of those states manifests.Moreover,by comparing the remaining negativities of the special quantum states with that of random pure states,we find that the statesare the most robust states and the statesare the most fragile ones.
Similarly,for bit flip channel,the statesandalso exhibit the most significant difference in robustness,but,contrary to the case of the dephasing channel,the statesare the most robust states,while the statesare the most fragile ones.Remarkably,our results suggest that the robustness of an arbitrary n-qubit system under decoherence can be greatly enhanced by LU operations.It might provide a possible way in protecting the robust n-qubit states against decoherence through appropriate LU operations.
Appendix A:Special statesandunderbit flip channel
The nonzero elements of the partial transposed density matrixof the statein Eq.(13)under the influence of bit flip channel can read as follows:
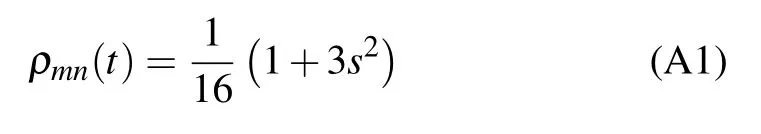
with m,n=1,16 and m,n=8,9;
where m=1,n=8;m=8,n=16;m=9,n=1,and m=16,n=9,and
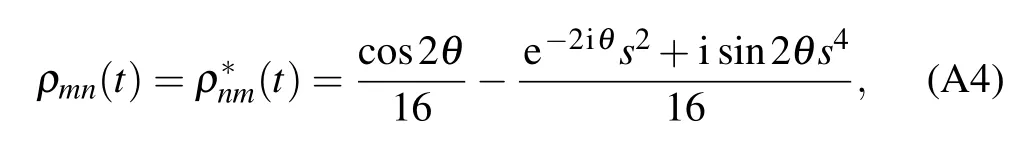
The nonzero elements of the partial transposed density matrixof the statein Eq.(5)under the bit flip channel can read as follows:

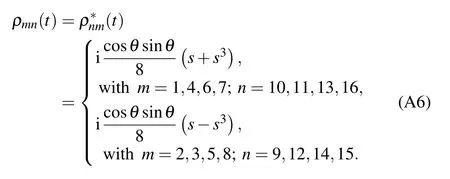
- Chinese Physics B的其它文章
- Theoretical analyses of stock correlations affected by subprime crisis and total assets:Network properties and corresponding physical mechanisms?
- Influence of matrigel on the shape and dynamics of cancer cells
- Benefit community promotes evolution of cooperation in prisoners’dilemma game?
- Theory and method of dual-energy x-ray grating phase-contrast imaging?
- Quantitative heterogeneity and subgroup classification based on motility of breast cancer cells?
- Designing of spin filter devices based on zigzag zinc oxide nanoribbon modified by edge defect?

