DYNAMICS FOR AN SIR EPIDEMIC MODEL WITH NONLOCAL DIFFUSION AND FREE BOUNDARIES?

(趙孟)

College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China E-mail:zhaom@nwnu.edu.cn

Wantong LI (李萬(wàn)同)?

School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China E-mail:wtli@lzu.edu.cn

Jiafeng CAO (曹佳峰)

Department of Applied Mathematics,Lanzhou University of Technology,Lanzhou 730050,China E-mail:caojf07@lzu.edu.cn

Abstract This paper is concerned with the spatial propagation of an SIR epidemic model with nonlocal diffusion and free boundaries describing the evolution of a disease.This model can be viewed as a nonlocal version of the free boundary problem studied by Kim et al.(An SIR epidemic model with free boundary.Nonlinear Anal RWA,2013,14:1992–2001).We first prove that this problem has a unique solution de fined for all time,and then we give sufficient conditions for the disease vanishing and spreading.Our result shows that the disease will not spread if the basic reproduction number R0<1,or the initial infected area h0,expanding abilityμ,and the initial datum S0are all small enough when.Furthermore,we show that if,the disease will spread when h0is large enough or h0is small butμis large enough.It is expected that the disease will always spread when R0,which is different from the local model.

Key words SIR model;nonlocal diffusion;free boundary;spreading and vanishing

1 Introduction

In mathematical epidemiology,one of the most important models is the classical SIR model,which receives great attention.In this model,according to the stage of infection,the population is separated into three classes:susceptible,infectious and recovered individuals,denoted by

S,I

and

R

,respectively.Assuming that the disease incubation period is negligible so that each susceptible individual becomes infectious and later recovers having acquired a permanent or temporary immunity,then the classical SIR model can be governed by

is a threshold value for the longtime behaviour of(1.1),the disease will die out if

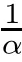
R

<

1,and remain endemic if

R

>

1.Obviously,(1.1)ignores the spatial diffusion of the population.Motivated by this factor,Kuniya and Wang[21]studied the corresponding spatial diffusion problem,and obtained a result similar to[15]for some special cases.To describe how an epidemic spreads in space,spreading speed is an useful approach.We refer to Hosono and Ilyas[16]for the spreading speed of a corresponding spatial diffusion problem.However,the works of Kuniya and Wang[21]and Hosono and Ilyas[16]cannot describe precisely the spreading front of the disease.This shortcoming can be overcome by considering the problem over a moving domain,resulting in the free boundary problem.Kim et al.[20]introduced the free boundary in order to consider the corresponding spatial diffusion problem;that is to say,they assume that the populations

S,I

and

R

disperse randomly,and the range of infected area is assumed to be a moving interval,

B

(0).This model has the form

where the free boundaries satisfy the famous Stefan condition.Kim et al.first proved the existence and uniqueness of the global solution,and then gave the sufficient conditions for the disease vanishing or spreading:

(i)If

R

<

1,then

h

<

∞.(ii)If

R

>

1,then there exist

h

and

h

such that(a)if

h

>h

,then

h

=∞;(b)if

h

≤

h

,then there exists

μ

>

0 such that

h

<

∞for 0

<μ<μ

,where

R

is given by(1.2).Moreover,if

h

<

∞,then

The results in[20]seem to be more reasonable than those in[15].Later,Huang and Wang[17]studied a similar SIR epidemic model with a free boundary in one dimension.They obtained some sufficient conditions of disease vanishing,and then gave the longtime behavior of

S,I

and

R

if vanishing happens.For(1.3),the deduction of free boundary condition

h

(

t

)=?

μI

(

t,h

(

t

))can be found in[2].Du and Lin[6]were the first to use this condition to consider a logistic type of local diffusion model with a free boundary.After this work,many local diffusion problems with a free boundary were investigated;see[7,8,10–14,18,19,22,26–29,32–35]and the references therein.Recently,Cao et al.[3]proposed a nonlocal version of[6],and successfully extended many basic results of[6]to the nonlocal model.For the spreading-vanishing criteria,the results in[3]revealed signi ficant differences from the local diffusion model in[6].Very recently,Du et al.[5]investigated the spreading speed of the nonlocal model in[3]and proved that the spreading may or may not have a finite speed,depending on whether a certain condition is satis fied by the kernel function

J

.From these results,we can see that there are striking differences between the local and nonlocal diffusion models.

Motivated by the work[3],many researchers investigated other problems with nonlocal diffusion and free boundaries;for example,Du et al.[9]considered a class of two species of Lotka-Volterra models with nonlocal diffusion and common free boundaries,Li et al.[24]discussed a class of free boundary problem in relation to ecological models with nonlocal and local diffusions,Zhao et al.[36]studied a degenerate epidemic model with nonlocal diffusion and free boundaries,Cao et al.[4]considered the dynamics of a Lotka-Volterra competition model with nonlocal diffusion and free boundaries,Wang and Wang[30,31]studied free boundary problems with nonlocal and local diffusions,and[23]considered the dynamics of nonlocal diffusion systems with different free boundaries,and so on.

Inspired by the above works about nonlocal diffusion,the main purpose of this paper is to extend the results in[20]into the free boundary problem with nonlocal diffusion.For simplicity,we assume that the spatial region is one dimensional.If the spatial movement is described by a nonlocal diffusion operator(see[1,25])and

S,I

and

R

have the same diffusion rate,then we can propose the nonlocal variation of(1.3)as follows:

Here,the parameters

d,μ

and

h

are positive constants.It is assumed that the kernel function

J

:R→R is continuous and nonnegative,and has the properties

Furthermore,we assume that the initial function

S

(

x

)belongs to

and the initial functions

I

(

x

)and

R

(

x

)belong to

where[?

h

,h

]represents the initial infected area.We note that the detailed derivation of the free boundary conditions

h

(

t

)and

g

(

t

)in(1.4)can be found in[3].We will show that(1.4)has a unique solution de fined for all time,and then determine its longtime dynamical behaviour.It is emphasized that we apply the approach in[3,9,36]to deal with(1.4),which is different from[20].Note that the equations for

S

and

I

are fully decoupled from

R

in(1.4).Although we only need to consider the sub-system for

S

and

I

,the reaction functions are different from the above mentioned works considering systems with nonlocal diffusion.As a result,the arguments in this paper will be a little different.The main results of this paper are the following theorems:

Theorem 1.1

Suppose that(J)holds.Then,for any given

h

>

0,

S

∈Xand

I

,R

∈X,problem(1.4)has a unique positive solution(

S

(

t,x

)

,I

(

t,x

)

,R

(

t,x

)

,g

(

t

)

,h

(

t

))de fined for all

t>

0.It is easily seen that

h

(

t

)is monotonically increasing and that

g

(

t

)is monotonically decreasing.Therefore

are always well-de fined.Let us recall that

R

is given by(1.2),so we have

Theorem 1.2

Let the conditions of Theorem 1.1 hold and let(

S,I,R,g,h

)be the solution of(1.4).Assume further that

J

(

x

)

>

0 in R.Then we have

Note that

l

is determined by an eigenvalue problem(see(3.6)).

Finally,we first explain the differences between the model with nonlocal diffusion and the one with local diffusion based on the work[3,5,6].

Remark 1.3

We note that local diffusion is only suitable to describe short-range in the dispersal,however,nonlocal diffusion can be used to study long-range factors in the dispersal by choosing the kernel function

J

properly.Mathematically,the results in[3]showed that if the diffusion rate of the species is small enough,then spreading will always happen,which is very different from that which is described in[6].On the other hand,the results in[5]showed that the spreading may have an in finite speed,which is another difference from the local model.Biologically,this means that nonlocal diffusion of the species increases the chance of species spreading,compared with the case that the species only diffuses randomly.

For our results,we have the following two remarks discussing the differences between the local and nonlocal model:

Remark 1.5

Depending on the choice of the kernel function in the nonlocal diffusion operator,Du et al.[5]showed that the spreading speed of the nonlocal model in[3]is accelerated.It is expected that a similar result holds for(1.4),which presents an interesting problem.To check this result,we should first obtain the longtime behavior of(1.4)for when spreading happens.We will consider this in the future.The rest of this paper is organised as follows:in Section 2 we prove Theorem 1.1,namely,problem(1.4)has a unique solution de fined for all

t>

0;the longtime dynamical behaviour of(1.4)is investigated in Section 3,where Theorem 1.2 is proved.

2 Global Existence and Uniqueness

Throughout this section,we assume that

h

>

0,

S

∈Xand

I

,R

∈X.For any given

T>

0,we first introduce the following notations: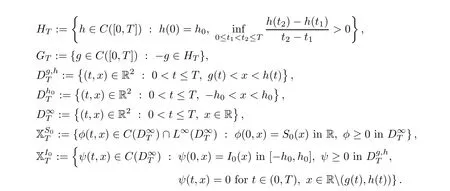

Just as in[3],we first prove the following lemma:

Lemma 2.1

For any given

T>

0 and(

g,h

)∈

G

×

H

,the problem

with

μ

=min{

μ

,μ

,μ

}.

Proof

If we can obtain the existence and uniqueness of(

S,I

),then the existence and uniqueness of

R

can follow from[36,Lemma 2.2].Hence we only need to consider problem

and prove the existence and uniqueness of solution(

S,I

).Let

f

(

S,I

)=

b

?

βSI

?

μ

S

and

f

(

S,I

)=

βSI

?

αI

?

μ

I

.Since

f

(0

,I

)/=0,and

S

is de fined in(0

,T

]×R,the corresponding result in[9]does not cover this case.However,we can deal with this by making some considerable changes.Here we give the details.

Step 1

The parameterised ODE problems.For any given

x

∈R and

s

∈(0

,T

],de fine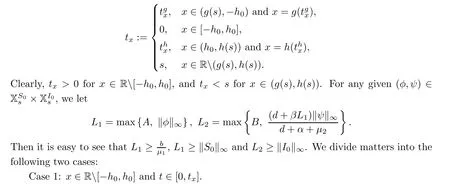

In this case,

I

(

t,x

)=0.Consider the following ODE initial value problem:

Case 2:

x

∈(

g

(

s

)

,h

(

s

))and

t

∈[

t

,s

].

De fine

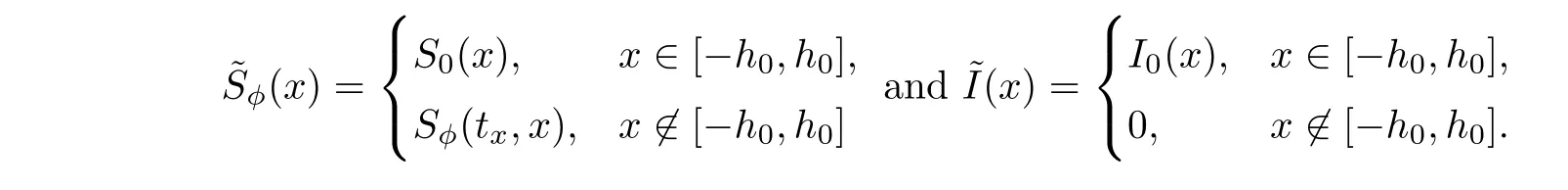
Consider the ODE problem

For any(

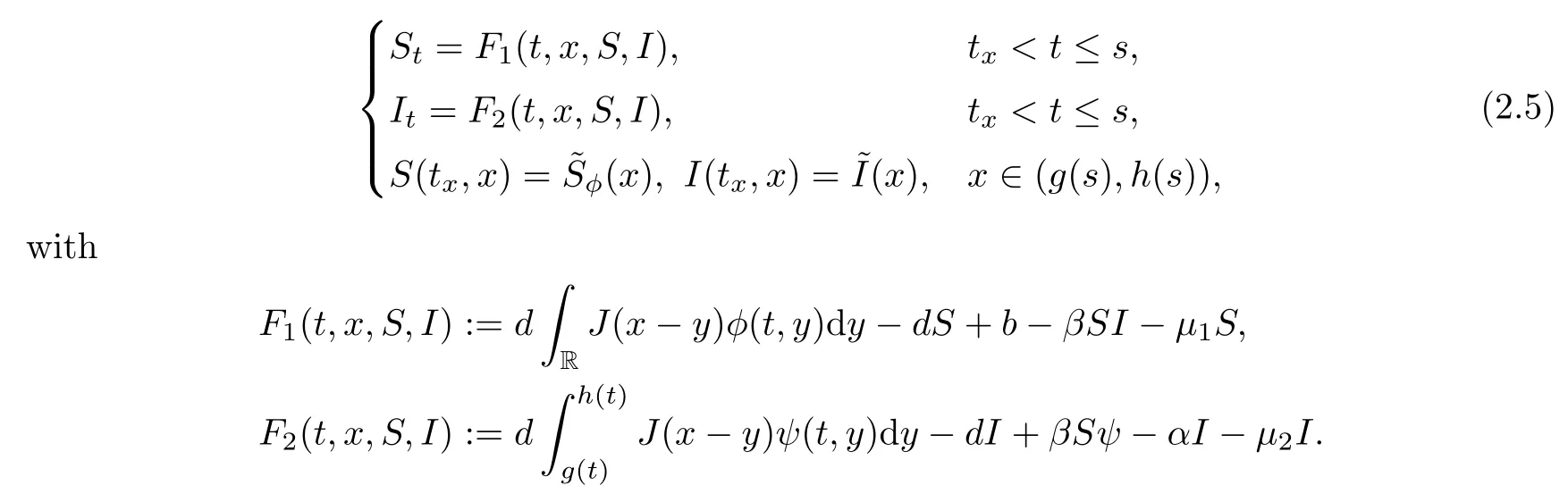
S

,I

)∈[0

,L

]×[0

,L

],

Hence,

F

(

t,x,S,I

)is Lipschitz continuous in(

S,I

)for(

S

,I

)∈[0

,L

]×[0

,L

],and is uniformly continuous for

x

∈(

g

(

s

)

,h

(

s

))and

t

∈[

t

,s

].Additionally,

F

(

t,x,S,I

)is continuous in all its variables in this range.By the fundamental theorem of ODEs,problem(2.5)admits a unique solution(

S

(

t,x

)

,I

(

t,x

))de fined in some interval[

t

,s

)of

t

,and(

S

(

t,x

)

,I

(

t,x

))is continuous in both

t

and

x

.To claim that

t

→(

S

(

t,x

)

,I

(

t,x

))can be uniquely extended to[

t

,s

],we should show that if(

S

,I

)is uniquely de fined for

t

∈[

t

,t

?]with?

t

∈(

t

,s

],then

It is easy to check that

By

L

≥‖

S

‖and

L

≥‖

I

‖,it follows from a simple comparison argument that

S

(

t,x

)≤

L

,I

(

t,x

)≤

L

in

t

∈[

t

,t

?].The left part can be obtained similarly by using

F

(

t,x,

0

,

0)≥0.

Step 2

A fixed point theorem.For any

s

∈(0

,T

),we denote

and‖

S

‖+‖

I

‖≤

B

,we can apply a simple comparison argument to see that

W

(

t,x

)≤

B

for

t

∈[0

,s

]and

x

∈[

g

(

t

)

,h

(

t

)].Hence,(2.11)holds.We have thus proved that for any

s

∈(0

,s

],(2.3)has a unique solution for

t

∈[0

,s

].

Step 3

Extension of the solution.

Proof of Theorem 1.1

Following the approach of[3],we will make use of Lemma 2.1 and a fixed point argument to finish this proof.For any given

T>

0 and(

g

,h

)∈

G

×

H

,it follows from Lemma 2.1 that(2.1)with(

g,h

)=(

g

,h

)has a unique solution(

S

,I

,R

).Using such

I

(

t,x

),we can de fine(

g

?

,

?

h

)for

t

∈[0

,T

]by

Due to the fact that,by(J),

J

(0)

>

0,there exist constants

?

∈(0

,h

/

4)and

δ

such that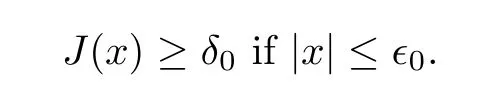

Using this,we can follow the corresponding arguments of[3]to show that,for some sufficiently small

T

=

T

(

μ,B,h

,?

,I

,J

)

>

0 and any

T

∈(0

,T

],

In what follows,we show that for sufficiently small

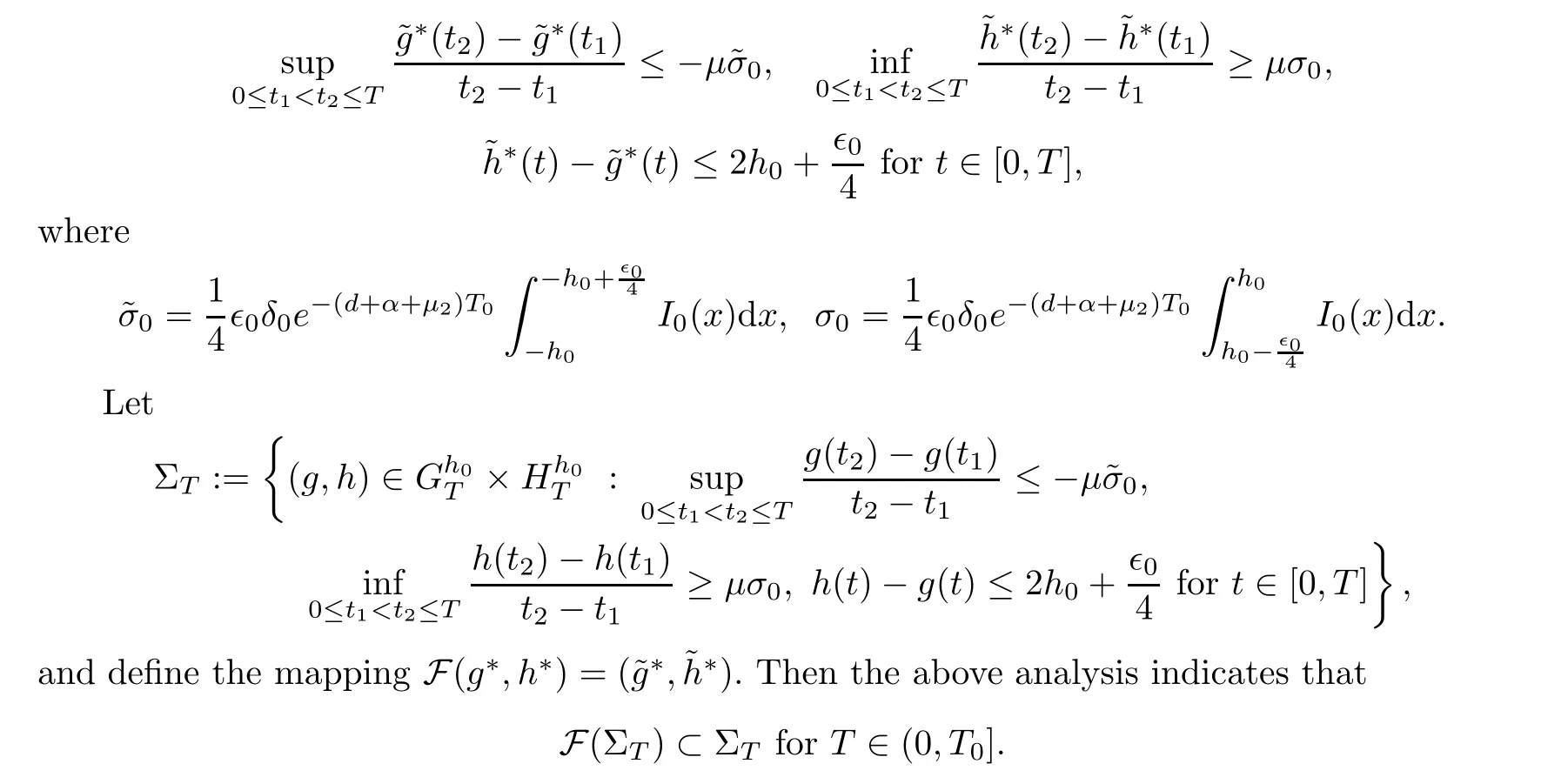
T

∈(0

,T

],F has a unique fixed point(

g

,h

)in Σ,so(

S

,I

,R

,g

,h

)clearly is a solution of(1.4)for

t

∈[0

,T

].We will then show that this is the unique solution of(1.4)and that it can be extended uniquely to all

t>

0.We will complete this task in several steps.

Step 1

We show that,for sufficiently small

T

∈(0

,T

],F has,by the contraction mapping theorem,a unique fixed point in Σ.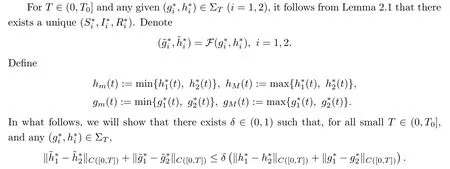

It follows from[36,(2.28)]that there exists some

C

depending on(

μ,h

,B

)such that

By the same argument as in[36],we deduce that,for

t

∈(0

,T

],

with

C

depending on(

d,α,β,μ

,A,B

).By[36,(2.16)],we have

Without loss of generality we may assume that

T

≤1.Then the inequalities(2.15),(2.16)and(2.17)yield,for the case

x

∈[?

h

,h

(

t

)],that

Here

C

does not depend on

T

and(

t

,x

).When

x

∈[

g

(

t

)

,

?

h

),we can show that this inequality still holds.Since

Z

(

t

,x

)=0 for

t

∈[0

,T

]and

x

∈R[

g

(

t

)

,h

(

t

)],we have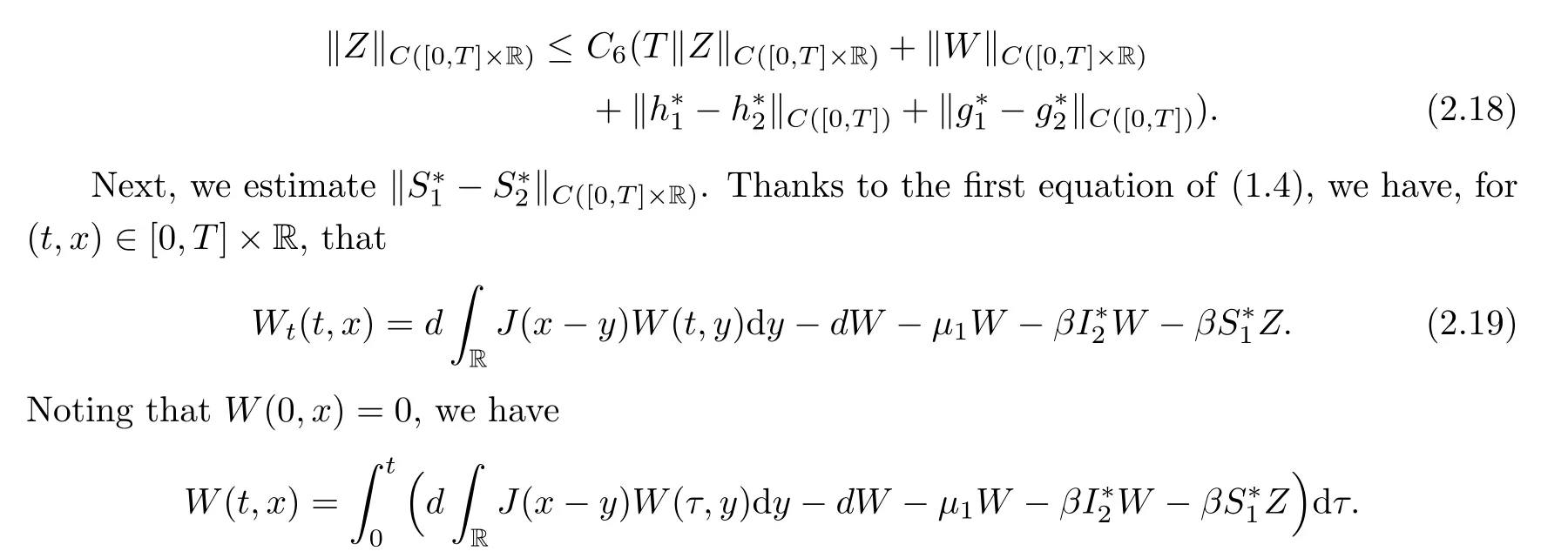

Thus,for

T

∈(0

,T

?],F is a contraction mapping on Σ.Hence,F has a unique fixed point(

g,h

)in Σ,which gives a nonnegative solution(

S,I,R,g,h

)of(1.4)for

t

∈(0

,T

].

Step 2

To show that(

S,I,R,g,h

)is the unique solution of(1.4)for

t

∈(0

,T

],we should show that(

g,h

)∈Σhold for any solution(

S,I,R,g,h

)of(1.4)de fined in

t

∈(0

,T

].This can be shown by the same argument as in Step 3 of the proof in[3,Theorem 2.1].Let(

S,I,R,g,h

)be an arbitrary solution of(1.4)de fined for

t

∈(0

,T

].Then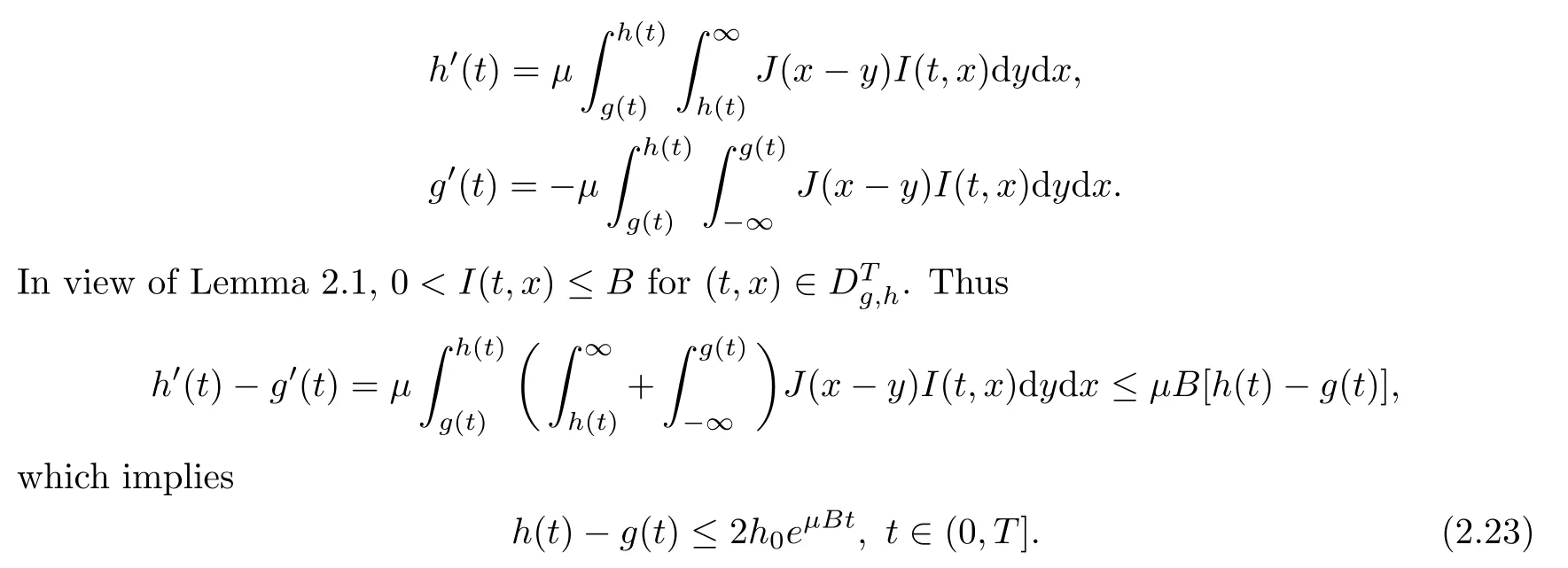

Step 3

Extension of the solution of(1.4)to

t

∈(0

,

∞).

Firstly,we can show,as above,that

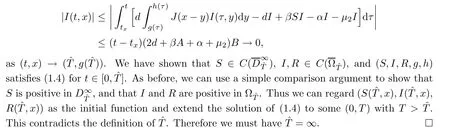
3 Spreading and Vanishing

Proof

Applying Lemma 3.1,we can prove this lemma by the same argument as in[3,Theorem 3.1]and[36,Lemma 3.2].Here we omit the proof.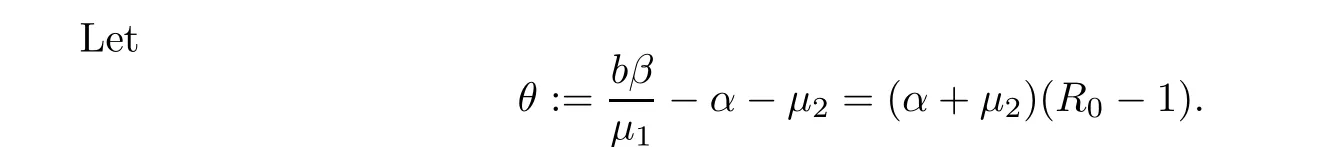

Lemma 3.3

If

θ<

0,or equivalently,

R

<

1,then

h

?

g

<

∞,and

Proof

We first prove(3.1).We note that

S

(

t,x

)satis fies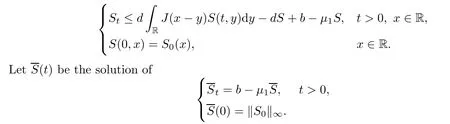

Then we can get

h

?

g

<

∞by letting

t

→∞.For the case

θ>

0,or equivalently,

R

>

1,we de fine the operator L+

θ

by

The generalized principal eigenvalue of L+

θ

is given by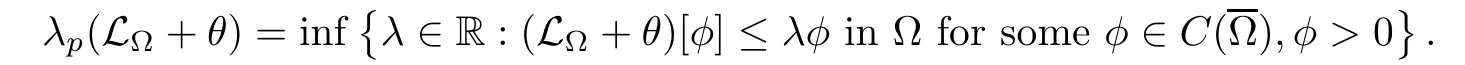

Lemma 3.4

Assume that

J

(

x

)satis fies(J),and that

J

(

x

)

>

0 in R.Let(

S,I,R,g,h

)be the solution of(1.4).If 0

<θ<d

and

h

?

g

<

∞,then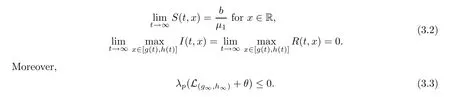

Proof

By the same arguments as in[9],we can have that

If we choose

δ

small enough such that

δφ

(

x

)≤

I

(

T

,x

)for

x

∈[

g

+

?,h

?

?

],then we can use[3,Lemma 3.3]and a simple comparison argument to obtain

This is in contradiction to(3.2).Thus we have proven(3.3).

We next consider the case 0

<θ<d.

In this case,it follows from[3,Proposition 3.4]that there exists

l

such that

Proof

(i)Arguing indirectly,we assume that

h

?

g

>l

.Since 0

<θ<d

,we have

λ

(L+

θ

)

>

0.This is in contradiction to(3.3).

(ii)This conclusion follows directly from(i).

(iii)By using[9,Lemma 3.9],we can have that there exists

μ

such that

h

?

g

=∞for

μ>μ

.Now we prove the remaining part.Since 2

h

<l

,we have

λ

(L+

θ

)

<

0.There exists some small

ε

such that

h

:=

h

(1+

ε

)satis fies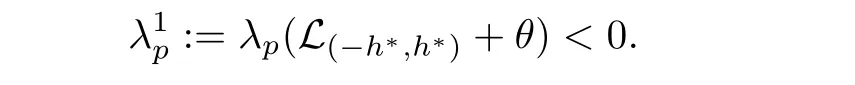

Choose the positive constants

K

large enough such that

For

δ

determined above,we choose

K

such that