ON A COUPLED INTEGRO-DIFFERENTIAL SYSTEM INVOLVING MIXED FRACTIONAL DERIVATIVES AND INTEGRALS OF DIFFERENT ORDERS?
Nonlinear Analysis and Applied Mathematics(NAAM)-Research Group,Department of Mathematics,Faculty of Science,King Abdulaziz University,P.O.Box 80203,Jeddah 21589,Saudi Arabia E-mail:bashirahmad qau@yahoo.com
Ravi P.AGARWAL
Department of Mathematics,Texas A&M University,Kingsville,Texas 78363-8202,USA E-mail:Ravi.Agarwal@tamuk.edu
Abrar BROOM Ahmed ALSAEDI
Nonlinear Analysis and Applied Mathematics(NAAM)-Research Group,Department of Mathematics,Faculty of Science,King Abdulaziz University,P.O.Box 80203,Jeddah 21589,Saudi Arabia E-mail:abrarbroom1992@gmail.com;aalsaedi@hotmail.com
Abstract By applying the standard fixed point theorems,we prove the existence and uniqueness results for a system of coupled differential equations involving both left Caputo and right Riemann-Liouville fractional derivatives and mixed fractional integrals,supplemented with nonlocal coupled fractional integral boundary conditions.An example is also constructed for the illustration of the obtained results.
Key words Fractional differential equations;Caputo and Riemann-Liouville fractional derivatives;systems;existence;fixed point theorems
1 Introduction
In this paper,we discuss the existence of solutions for a coupled system of nonlinear fractional differential equations,involving both left Caputo and right Riemann-Liouville fractional derivatives and mixed fractional integrals,equipped with nonlocal coupled fractional integral boundary conditions.In precise terms,we investigate the following system:
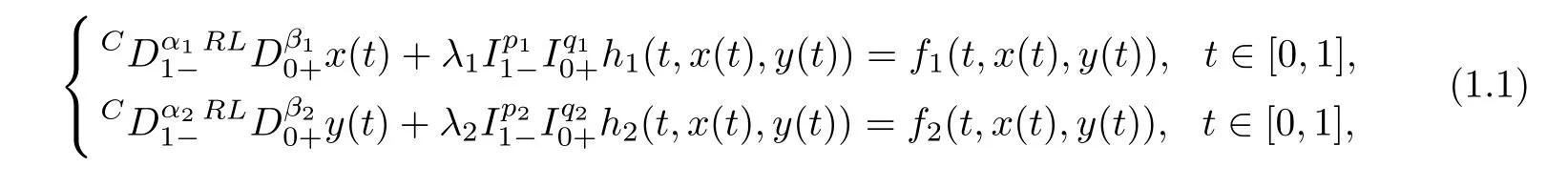
subject to integral boundary conditions:

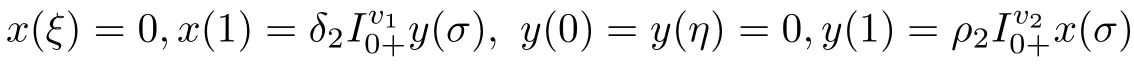
Before proceeding further,let us dwell some recent advancement in the study of fractional-order boundary value problems.The literature on the topic mainly deals with Caputo,Riemann-Liouville and Hadamard type fractional derivatives;for instance,see the texts[2–4]and articles[5–12].Fractional differential systems appear in the mathematical modeling of many real-world problems[13–15].For theoretical treatment of such systems,we refer the reader to the papers[16–18]and the references cited therein.In a recent article[19],the authors discussed the existence of solutions for the following systems of Caputo and Riemannn-Liouville type mixed order coupled fractional differential equations and inclusions:
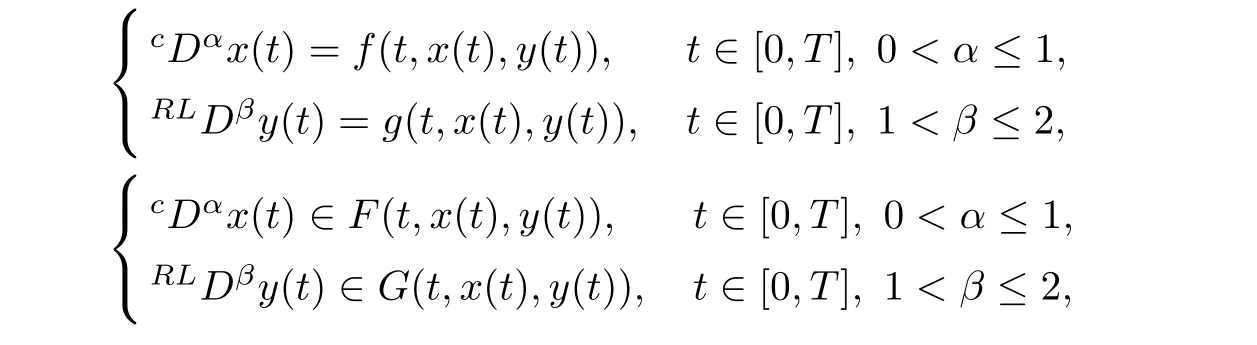
x
(0)=λ
D
y
(η
),y
(0)=0,y
(T
)=γI
x
(ξ
),λ,γ
∈R,η,ξ
∈(0,T
),
whereD
,
D
are the Caputo fractional derivatives of orderα
andp
∈(0,
1)respectively,D
is the Riemann-Liouville fractional derivatives of orderβ,I
is the Riemann-Liouville fractional integral of orderq>
0,f,g
:[0,T
]×R×R→R,F,G
:[0,T
]×R×R→P(R)are the given continuous functions,and P(R)is the family of all nonempty subsets of R.
On the other hand,boundary value problems of differential equations involving both left and right fractional derivatives of different orders and fractional integrals need further attention in view of the importance of these equations in the study of variational principles and Euler–Lagrange equations[20].In a recent article[21],the authors used the left-sided and rightsided fractional derivatives to formulate the fractional diffusion-advection equation related to anomalous superdiffusive transport phenomena.One can find some recent results on this class of boundary value problems in the articles[22–25].
The rest of this paper is organized as follows:in Section 2,we prove an auxiliary lemma,which plays a key role in converting the given problem to a fixed-point problem.Main results for our problem,presented in Section 3,are proved by means of Krasnoselskii’s fixed point theorem and contraction mapping principle.This paper concludes with illustrative examples.
2 An Auxiliary Lemma
Before presenting an auxiliary lemma,we recall some related de finitions from fractional calculus[2].
De finition 2.1
The left and right Riemann-Liouville fractional integrals of orderβ>
0 forg
∈L
[a,b
],
existing almost everywhere on[a,b
],
are respectively de fined by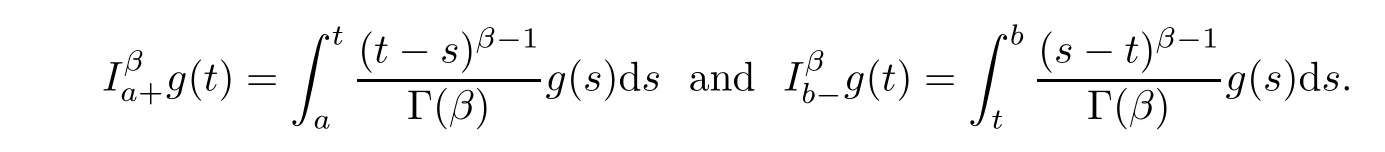
Lemma 2.2
Forg
∈L
[a,b
],
1≤p<
∞andq
,q
>
0,the following relations hold almost everywhere on[a,b
]: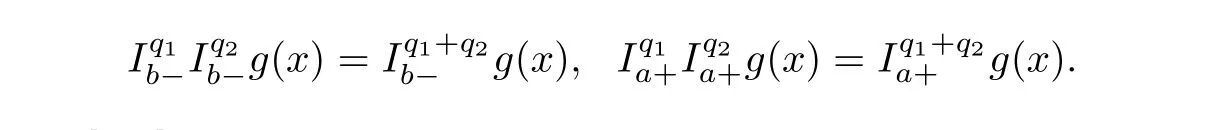
g
∈C
[a,b
]orq
+q
>
1,then the above relations hold for eachx
∈[a,b
].
De finition 2.3
Forg
∈AC
[a,b
],
the left Riemann-Liouville and the right Caputo fractional derivatives of orderβ
∈(n
?1,n
],n
∈N,
existing almost everywhere on[a,b
],
are respectively de fined by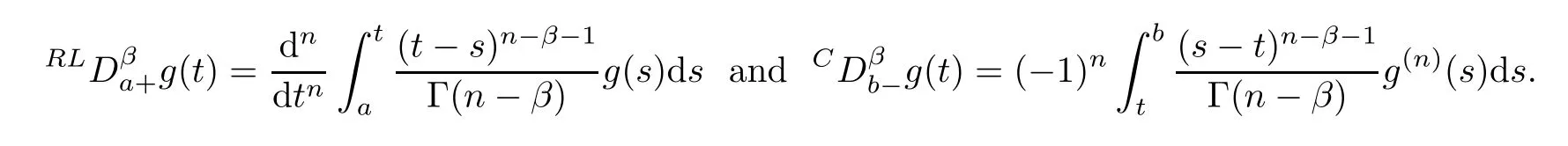
In the following lemma,we solve a linear variant of system(1.1)–(1.2).
Lemma 2.4
LetF
,F
,H
,H
∈C
([0,
1],
R).Then,the unique solution of the linear system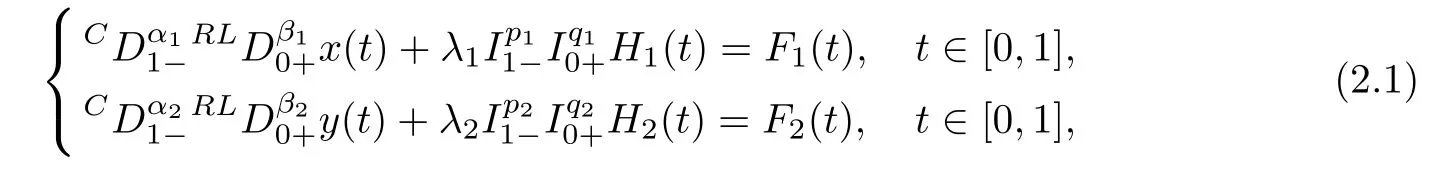
subject to the boundary conditions(1.2)is given by



c
,c
,c
,c
,c
andc
in(2.9)and(2.10)and using the notations(2.4),we get solutions(2.2)and(2.3).The converse follows by direct computation.This completes the proof.3 Main Results
Let X=C
([0,
1],
R)denote the Banach space of all continuous functions from[0,
1]→R equipped with the norm‖x
‖=sup{|x
(t
)|:t
∈[0,
1]}.
The product space(X×X,
‖(x,y
)‖)is also Banach space endowed with norm‖(x,y
)‖=‖x
‖+‖y
‖.
In view of Lemma 2.4,we de fine an operator Q:X×X→X×X as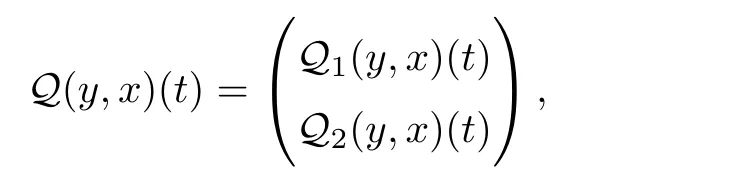

For computational convenience,we set
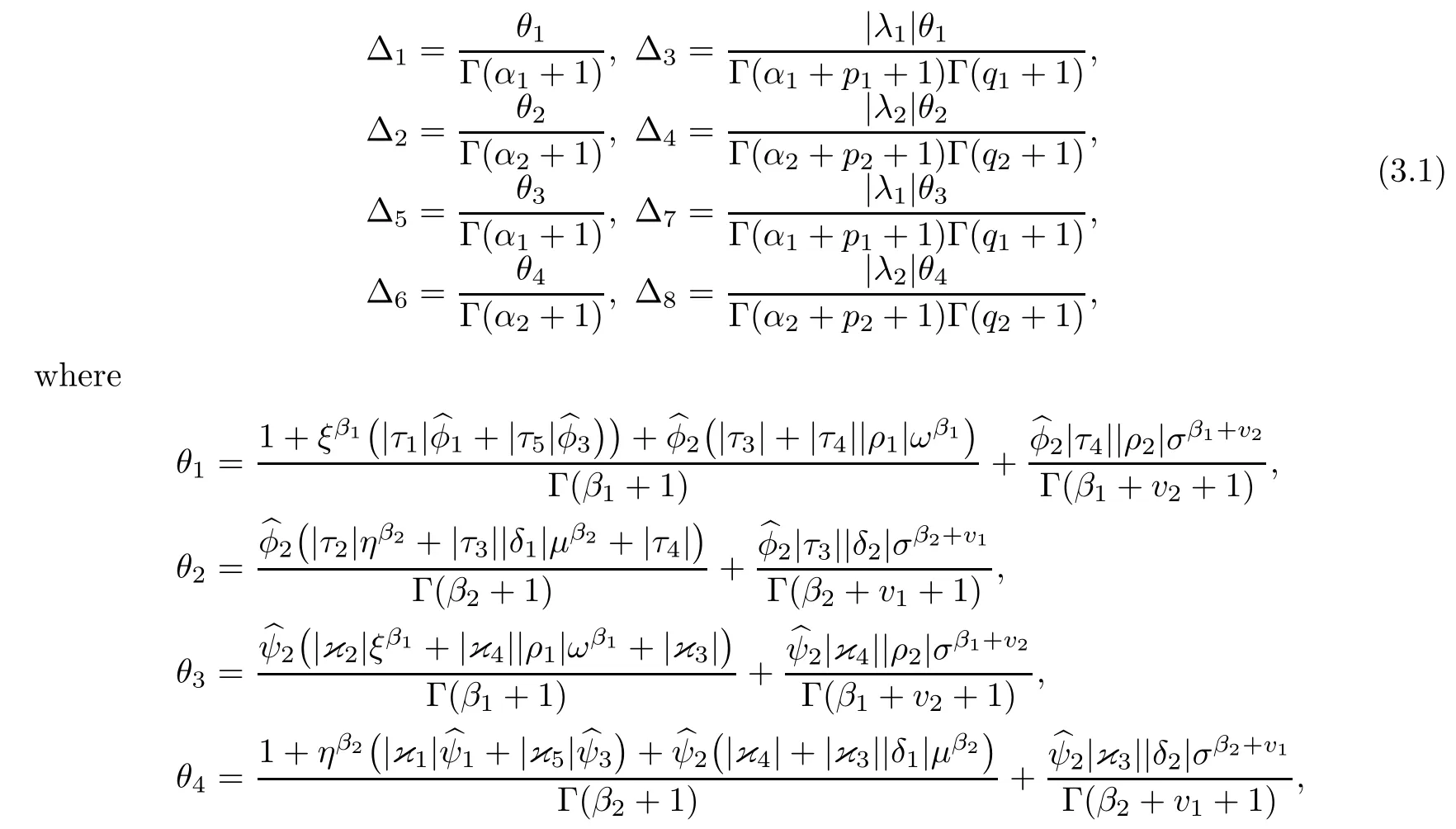
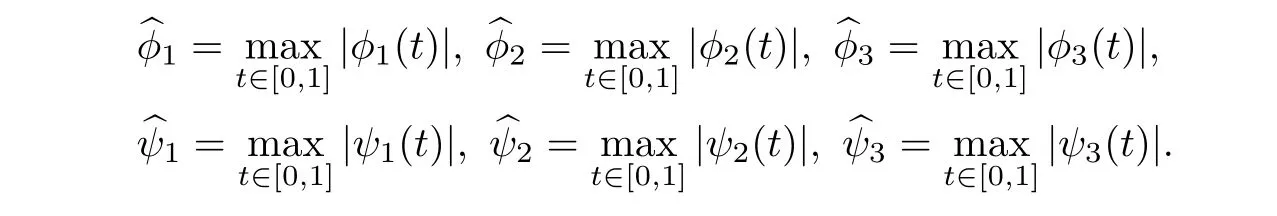
In the sequel,we need the following assumptions:
(S
)Letf
,h
:[0,
1]×R×R→R(i
=1,
2)be the real valued continuous functions such that,for allt
∈[0,
1]andx,y
∈R,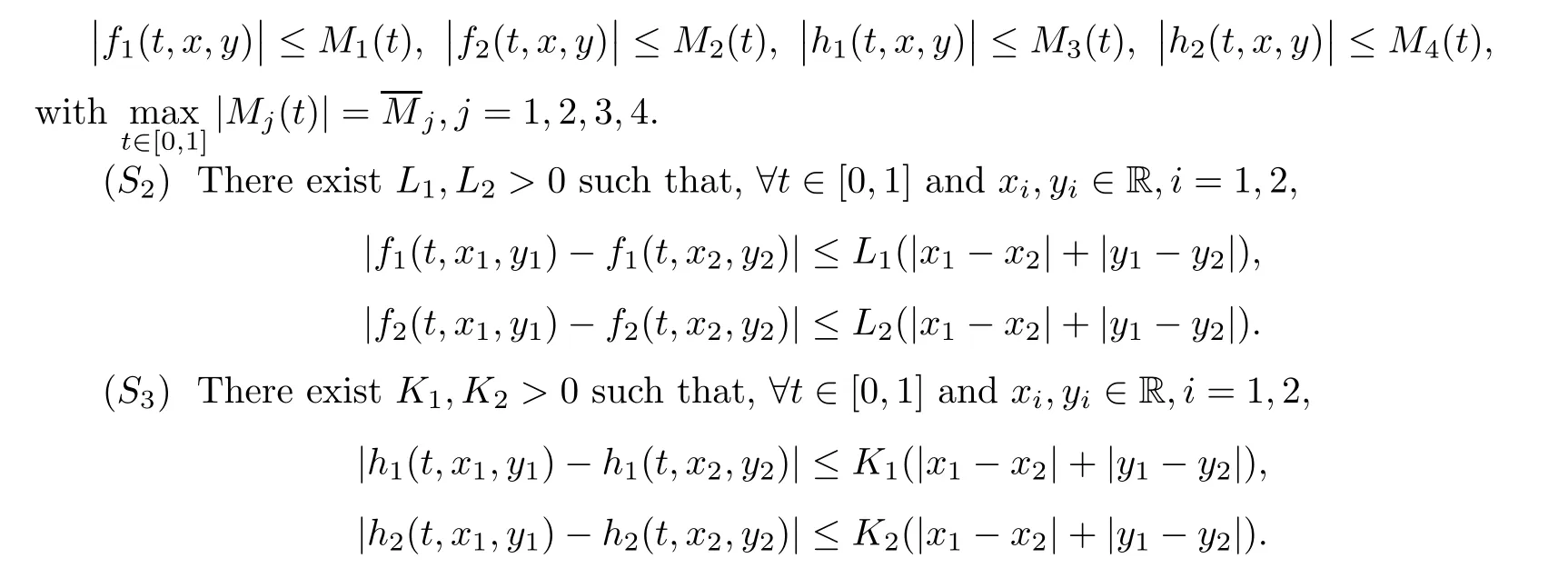
In the following theorem,we prove an existence result for system(1.1)–(1.2)via Kras-noselskii’s fixed point Theorem.For the reader’s convenience,we provide the statement of Kras-noselskii’s fixed point Theorem below.
Lemma 3.1
(Krasnoselskii[26])Let X be a closed,hounded,convex and nonempty subset of a Banach space у.Let H,Hbe operators mapping X to у such that(a)Hz
+Hz
∈X forz
,z
∈X;(b)His compact and continuous;
(c)His a contraction mapping.
Then there existsz
∈X such thatz
=Hz
+Hz
.Theorem 3.2
Suppose that(S
),(S
)and(S
)hold.Then,system(1.1)–(1.2)has at least one solution on[0,
1]provided that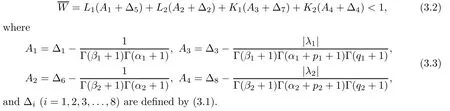
Proof
Introduce a closed,bounded and convex subset of X×X as


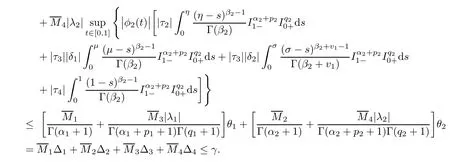
Similarly,we can find that
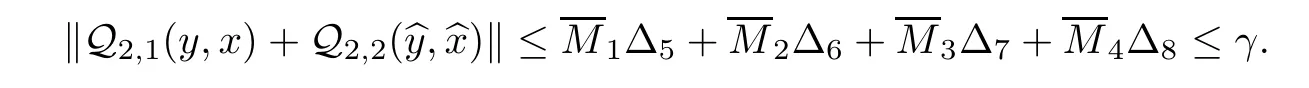
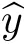
S
)and(S
).For(x
,y
),
(x
,y
)∈B,we have that

Likewise,we can obtain
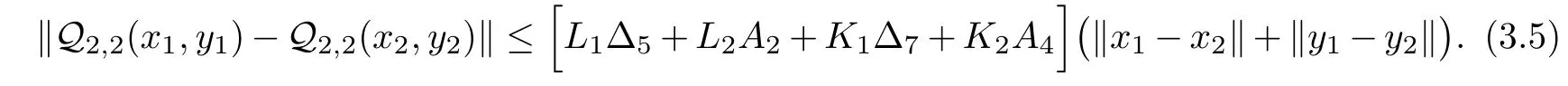
From(3.4)and(3.5),we deduce that
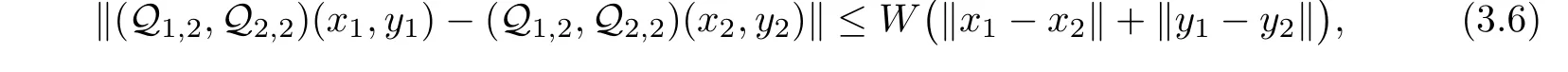
f
,f
,h
,h
,the operator(Q,Q)is continuous.For(x,y
)∈B,we have
In consequence,we have
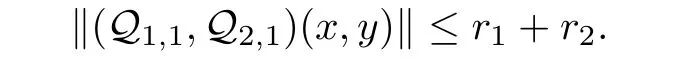
<t
<t
<
1 and?(x,y
)∈B,we obtain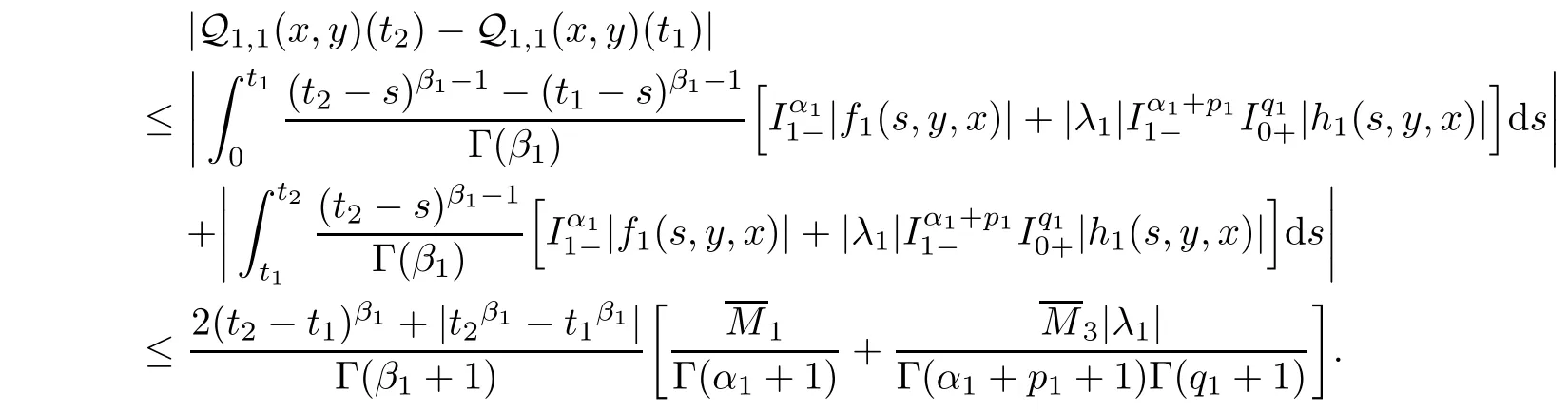
Analogously,we can find that
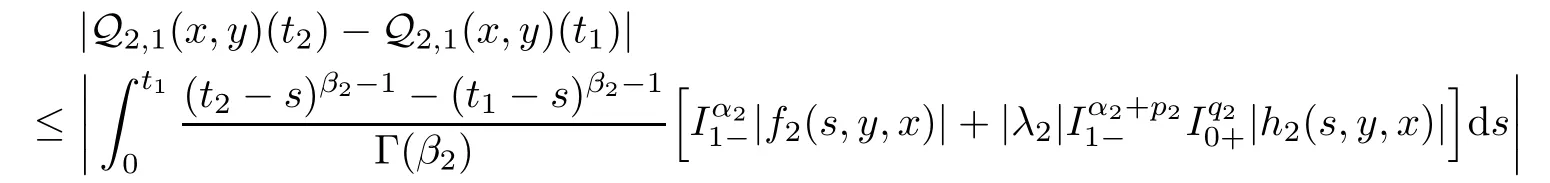
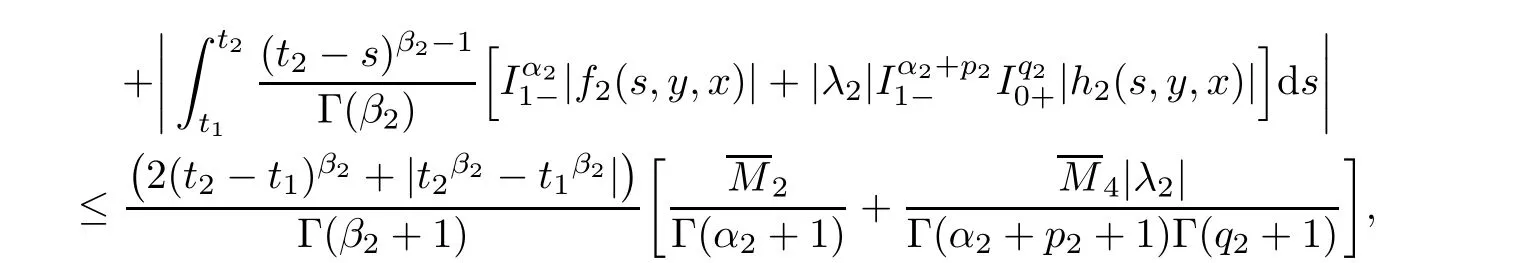
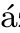
Now,we prove the uniqueness of solutions for system(1.1)–(1.2)via the Banach contraction mapping principle.
Theorem 3.3
Letf
,f
,h
,h
:[0,
1]×R×R→R be continuous functions satisfying assumptions(S
)and(S
).Then,problem(1.1)–(1.2)has a unique solution on[0,
1]ifW<
1,
where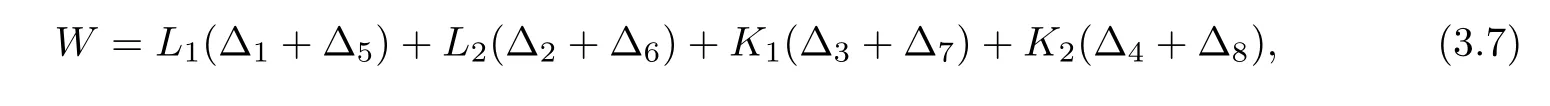
i
=1,
2,...,
8)are de fined by(3.1).Proof
Let us fix a positive numberr
such that

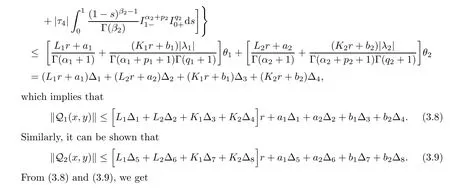
x,y
)‖≤Wr
+(?+?)a
+(?+?)a
+(?+?)b
+(?+?)b
<r,
which implies that Q(x,y
)∈Bfor any(x,y
)∈B.Therefore QB?B.Now,we prove that Q is a contraction.Let(x
,y
),
(x
,y
)∈X×X for eacht
∈[0,
1].
Then,by the conditions(S
)and(S
),we obtain

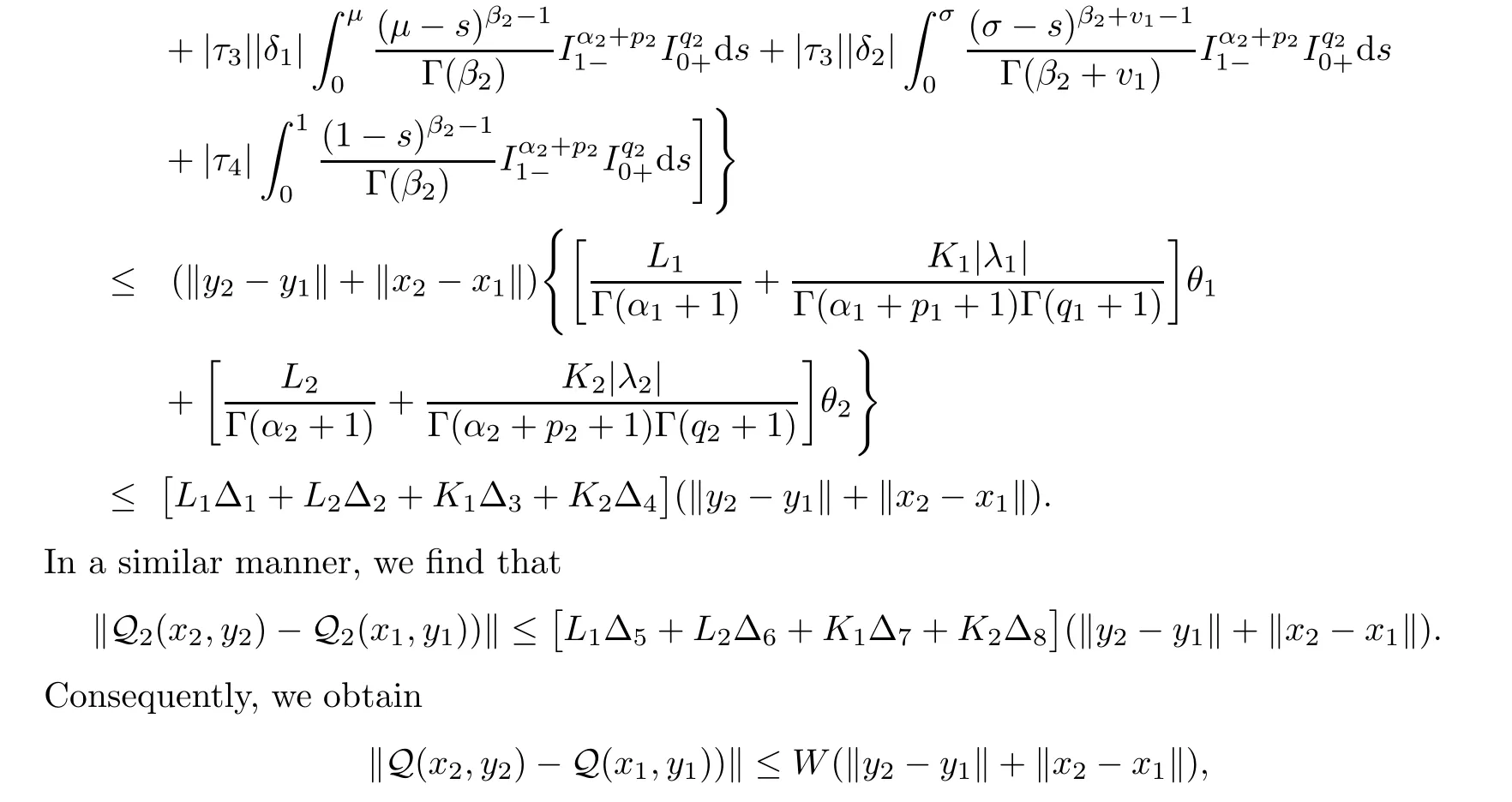
W<
1,
implies that Q is a contraction.Hence it follows by Banach fixed point theorem that the operator Q has a unique fixed point,which corresponds to a unique solution of problem(1.1)–(1.2)on[0,
1].
The proof is finished.4 Example
Consider a coupled system of fractional differential equations containing Caputo and Riemann-Liouville derivatives of fixed orders and supplemented with coupled fractional integral boundary conditions given by
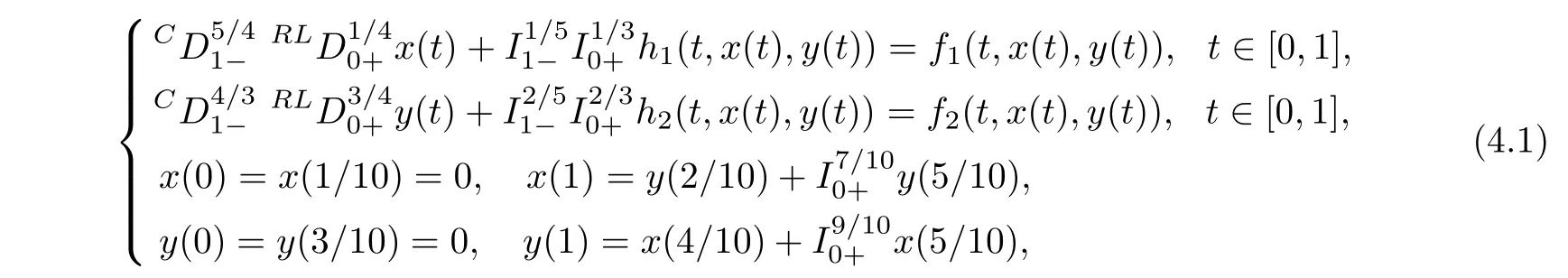
α
=5/
4,α
=4/
3,β
=1/
4,β
=3/
4,p
=1/
5,p
=2/
5,q
=1/
3,q
=2/
3,λ
=λ
=1,δ
=δ
=ρ
=ρ
=1,ξ
=1/
10,μ
=2/
10,η
=3/
10,ω
=4/
10,σ
=5/
10,v
=7/
10,v
=9/
10,
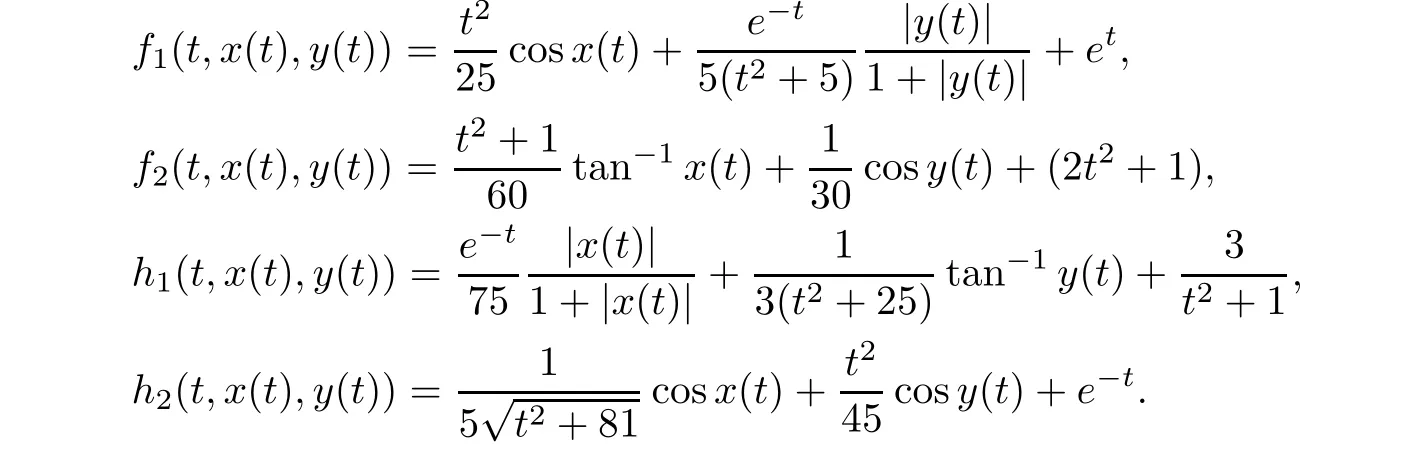
S
)is satisfied because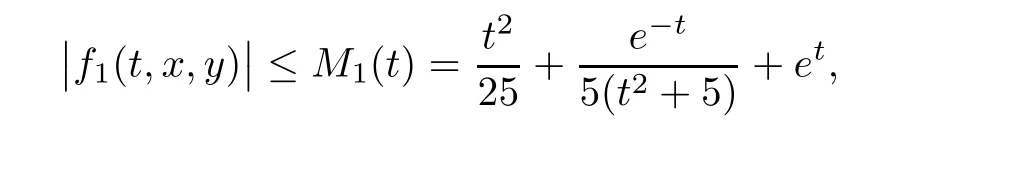
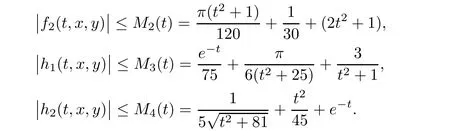
S
)and(S
)are satis fied withL
=1/
25,L
=1/
30,K
=1/
75,
andK
=1/
45.
With the given values,we find that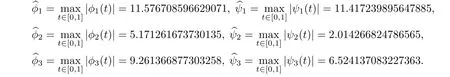
,i
=1,
2,...,
8(de fined by(3.1))are found to be
Using the given values,we get
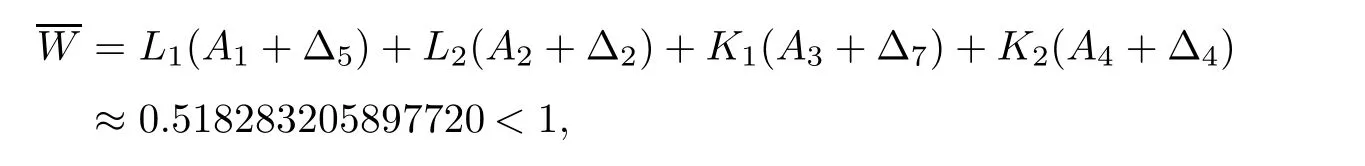
A
=3.
175697653501054,A
=3.
354900140842817,A
=3.
137567231307605,
andA
=2.
788768311529850.
Thus,all the conditions of Theorem 3.2 are satis fied and consequently,its conclusion applies to system(4.1).Also,W
≈0.
617403220956142<
1,
whereW
is de fined by(3.
7).Thus,the hypothesis of Theorem 3.3 is satisfied and hence its conclusion ensures that there exists a unique solution for system(4.1)on[0,
1].Acknowledgements
This project was funded by the Deanship of Scienti fic Research(DSR),King Abdulaziz University,Jeddah,Saudi Arabia under grant no.(KEP-MSc-63-130-42).The authors,therefore,acknowledge with thanks DSR technical and financial support. Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY OF WEAK SOLUTIONS TO A CLASS OF NONLINEAR PROBLEM?
- EXISTENCE TO FRACTIONAL CRITICAL EQUATION WITH HARDY-LITTLEWOOD-SOBOLEV NONLINEARITIES?
- A DIFFUSIVE SVEIR EPIDEMIC MODEL WITH TIME DELAY AND GENERAL INCIDENCE?
- CLASSIFICATION OF SOLUTIONS TO HIGHER FRACTIONAL ORDER SYSTEMS?
- ENERGY CONSERVATION FOR SOLUTIONS OF INCOMPRESSIBLE VISCOELASTIC FLUIDS?
- JULIA LIMITING DIRECTIONS OF ENTIRE SOLUTIONS OF COMPLEX DIFFERENTIAL EQUATIONS?
