JULIA LIMITING DIRECTIONS OF ENTIRE SOLUTIONS OF COMPLEX DIFFERENTIAL EQUATIONS?
(王珺)
School of Mathematical Sciences,Fudan University,Shanghai 200433,China E-mail:majwang@fudan.edu.cn
Xiao YAO (姚瀟)?
School of Mathematical Sciences and LPMC,Nankai University,Tianjin 300071,China E-mail:yaoxiao@nankai.edu.cn
Chengchun ZHANG (張城純)
School of Mathematical Sciences,Fudan University,Shanghai 200433,China E-mail:18210180014@fudan.edu.cn
Abstract For entire or meromorphic function f,a value θ∈[0,2π)is called a Julia limiting direction if there is an unbounded sequence{zn}in the Julia set satisfyingOur main result is on the entire solution f of P(z,f)+F(z)fs=0,where P(z,f)isadifferential polynomial of f with entire coefficients of growth smaller than that of the entire transcendental F,with the integer s being no more than the minimum degree of all differential monomials in P(z,f).We observe that Julia limiting directions of f partly come from the directions in which F grows quickly.
Key words Julia set;meromorphic function;Julia limiting direction;complex differential equations
1 Introduction and Main Results

There are a lot of works centered around the dynamics of classes of transcendental functions,such as the Speier class and the Eremenko-Lyubich class.This paper is another contribution in this direction,and we focus on transcendental entire solutions of complex differential equations.For these transcendental solutions,we investigate the geometric property of their Julia sets near∞,which is one of the questions in transcendental iteration theory distinct from the iteration of rational functions.
Baker[2]observed that,whenf
is a transcendental entire function,J(f
)cannot be contained in any finite set of straight lines.However,this is not true for transcendental meromorphic functions,such as J(tanz
)=R.From the viewpoint of angular distribution,Qiao[11]introduced the limiting direction of the Julia set.A valueθ
∈[0,
2π
)is said to be a limiting direction of the Julia set off
if there is an unbounded sequence{z
}?J(f
)such that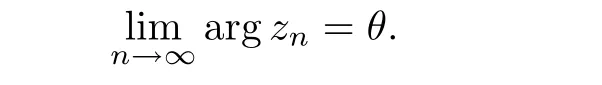
f
a Julia limiting direction off
.We denote byL
(f
)the set of all Julia limiting directions off
;it is a non-empty closed set in[0,
2π
)and will reveal the large-scale geometry property of J(f
).Since any rational function,as well as any polynomial,can be treated as a map between two Riemann spheres,it makes no sense for us to consider the Julia limiting direction for rational functions.Furthermore,we identify[0,
2π
)with the circle S:={z
∈C:|z
|=1}and intervals in[0,
2π
)with arcs on the circle for convenience.Value distribution theory plays an important role in studying transcendental meromorphic functions,and its standard notations as well as its well-known theorems can be found in[7,8].For example,we denote byT
(r,f
)andN
(r,f
)the characteristic function and the integrated counting function of poles,respectively,with respect tof
.The orderρ
(f
)and the lower orderμ
(f
)are de fined by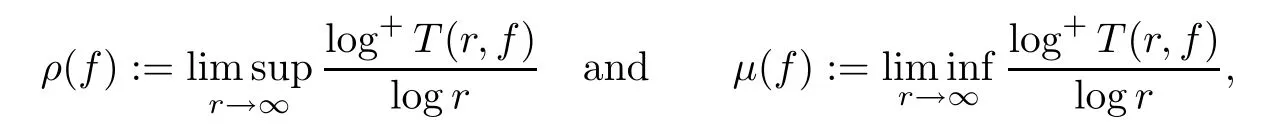
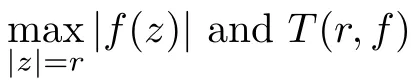
L
(f
)and the growth order off
.Theorem 1.1
([11])Letf
be a transcendental entire function of lower orderμ<
∞.Then there exists a closed intervalI
?L
(f
)such that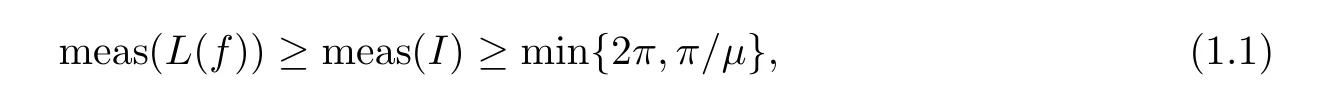
I
)is the Lebesgue measure of the setI
.The condition thatμ<
∞in Theorem 1.1 is necessary,since Baker[2]proved that there exists an entire functionf
of in finite lower order with a property implying thatL
(f
)is a single point set.Furthermore,Qiao[11]showed that the estimate in Theorem 1.1 is sharp,which is veri fied by modifying functions in the Mittag-Leffler class.Recalling J(tanz
)=R,Theorem 1.1 fails for general meromorphic functions,but under some certain conditions,Theorem 1.1 can be generalized;see[12,21]for the details.For entire functions of in finite lower order,what is the sufficient condition for the existence of the lower bound of meas(L
(f
))?There are already some considerations regarding solutions of complex differential equations,for example,the linear equations
(see[9]),and the nonlinear equations,such as Riccati equations

(see[20]).We only state the result on linear equations(1.2)here.
Theorem 1.2
([9])Suppose that all coefficients of(1.2)are entire functions of finite lower order,thata
is transcendental and thatT
(r,a
)=o
(T
(r,a
))(i
=1,
2,...,n
?1).Then every nonzero solutionf
of(1.2)is of in finite lower order,and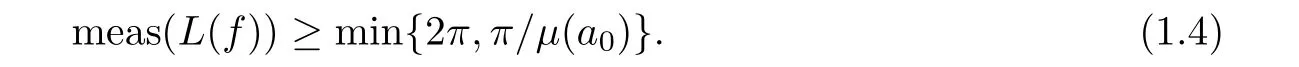
Furthermore,under the hypothesis of Theorem 1.2,there even exists(see[17])

f
(n
∈Z)denote the derivatives forn
∈N and the anti-derivatives for?n
∈N,andf
=f
.In addition,a corresponding investigation has been done for equations(1.2)with exponential coefficients[16].However,it is not clear what is behind the inequalities(1.1)and(1.4).Recently,we found out that for the entire functionf
,the direction in whichf
grows more quickly than any polynomial is a Julia limiting direction off
;see Lemma 2.2 in the next section.We introduce the following concept of transcendental direction to describe these directions in whichf
grows quickly:a valueθ
∈[0,
2π
)is said to be a transcendental direction off
if there exists an unbounded sequence of{z
}such that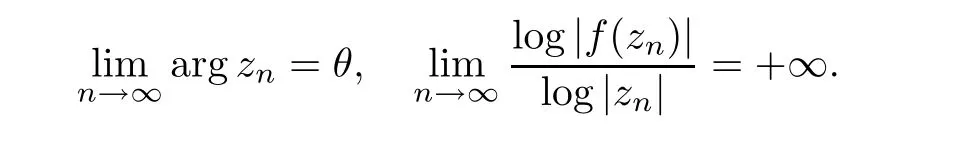
TD
(f
)to denote the union of all transcendental directions;clearlyTD
(f
)is a non-empty compact set in[0,
2π
).We will see that Julia limiting directions of solutions to(1.2)partly come from the transcendental directions of the dominanting coefficienta
.Furthermore,in this paper,we investigate more general differential equations,which even contain some non-linear differential equations.Before stating our results,we first introduce the terminology of differential polynomials off
.The differential polynomialP
(z,f
)is a finite sum of differential monomials generated byf
,that is,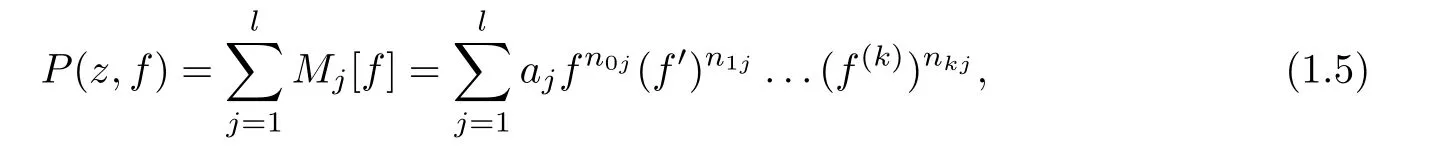
a
(z
)are meromorphic,and the powersn
,n
,...,n
are non-negative integers.We useγ
to denote the minimum degree ofM
as
Theorem 1.3
Suppose thats,n
are integers,F
(z
)is a transcendental entire function of finite lower order,and thatP
(z,f
)is a differential polynomial inf
withγ
≥s
,where all coefficientsa
(j
=1,
2,...,l
)are polynomials ifμ
(F
)=0,or alla
(j
=1,
2,...,l
)are entire functions andρ
(a
)<μ
(F
).Then,for every nonzero transcendental entire solutionf
of the differential equation
TD
(f
)∩TD
(F
)?L
(f
)and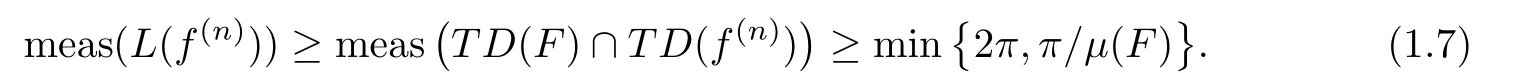
s
=1,F
=a
(z
)andP
(z,f
)=f
+a
(z
)f
+...
+a
(z
)f
,we immediately obtain the following corollary from Theorem 1.3:Corollary 1.4
Suppose that all coefficients of(1.2)are entire functions of finite lower order,thata
is transcendental and that alla
(i
=1,
2,...,n
?1)are polynomials ifμ
(a
)=0,or that alla
(i
=1,
2,...,n
?1)satisfyρ
(a
)<μ
(a
).Then,for every nonzero solutionf
of(1.2),we haveTD
(f
)∩TD
(a
)?L
(f
),k
∈Z and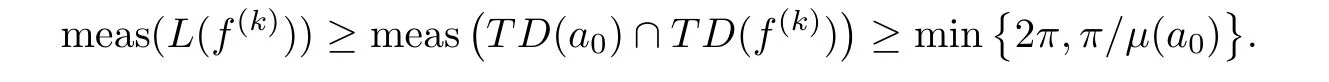
s
=0,there is another corollary from Theorem 1.3 which can treat not only the non-homogeneous linear equation corresponding to(1.2)but also the non-linear differential equationsP
(z,f
)=F
(z
).Corollary 1.5
Suppose thatF
andP
(z,f
)are de fined as in Theorem 1.3.Then,for every nonzero entire solutionf
of the equationP
(z,f
)=F
(z
),we haveTD
(f
)∩TD
(F
)?L
(f
),n
∈Z and(1.7).Remark 1.6
The general Riccati differential equationsf
=a
(z
)+a
(z
)f
+a
(z
)f
can be rewritten as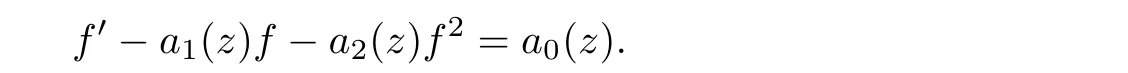
a
,a
,a
are entire functions of finite lower order such thatρ
(a
)<μ
(a
)andρ
(a
)<μ
(a
),then meas(L
(f
))≥min{2π,π/μ
(a
)}follows from Corollary 2.Clearly,(1.3)is different from our case of Riccati differential equation.The remainder of this paper is organized as follows:in Section 2,we show some basic properties of Julia limiting directions for entire functions,which contain the relation between transcendental directions and Julia limiting directions.The proof of Theorem 1.3 is given in Section 3,and some examples given here.Our method is somewhat different and simpler than that of[9,17].
2 Basic Property of Julia Limiting Directions
The relation betweenTD
(f
)andL
(f
)is important for our proof of Theorem 1.3.Before proving the theorem,we need a result which can be deduced from the proof of[11,Lemma 1]in order to deal with the case that F(f
)contains an angular domain.One Friday evening I came home from work to find a big beautiful German shepherd on our doorstep. This wonderful strong animal gave every indication that he intended to enter the house and make it his home. I, however, was wary4. Where did this obviously well-cared-for dog come from? Was it safe to let the children play with a strange dog? Even though he seemed gentle, he still was powerful and commanded respect. The children took an instant liking5 to German and begged me to let him in. I agreed to let him sleep in the basement until the next day, when we could inquire around the neighborhood for his owner. That night I slept peacefully for the first time in many weeks.
Lemma 2.1
Letf
be analytic in the angular domain
f
(?(z
,θ,δ
))is contained in a simply connected hyperbolic domain in C.Then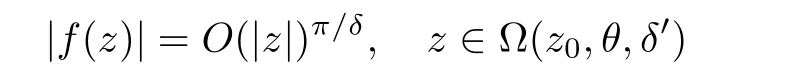
δ
∈(0,δ
).Now by Lemma 2.1,we establish the relation between transcendental directions and Julia limiting directions as follows:
Lemma 2.2
Letf
be a transcendental entire function.ThenTD
(f
)?L
(f
).Proof
We first treat the case in which F(f
)has a multiply connected component.We claim that in this case,L
(f
)=[0,
2π
).Otherwise,there exists one valueθ
/∈L
(f
),so there exist?>
0,a
∈C and arga
=θ
such that
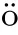
θ
∈TD
(f
),we assume thatθ
/∈L
(f
),so we have ?(a,θ,
2?
)?F(f
)for two constants?>
0 anda
with arga
=θ
.At the same time,there is an unbounded sequence{z
}??(a,θ,
2?
)such that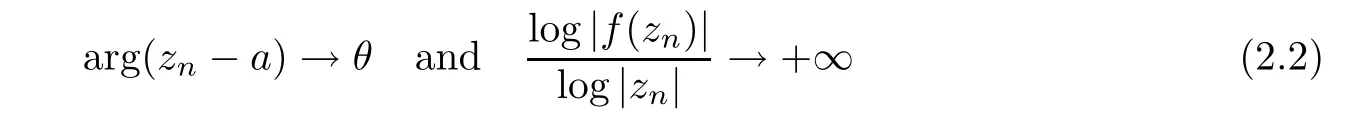
n
→∞.Clearly,f
(?(a,θ,?
))is contained in a simply connected hyperbolic domain.By Lemma 2.1,there exist positive constantsk
andA
such that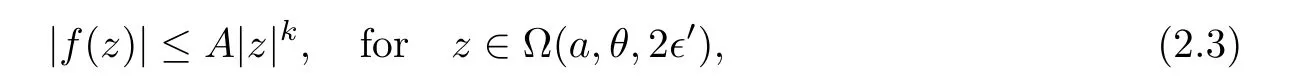
f
,we can investigate the Julia limiting directions by first finding the transcendental directions.By the radial growth ofe
,that is,|exp(re
)|=e
,it is easy to see thatL
(sinz
)=L
(cosz
)=[0,
2π
)sinceTD
(sinz
)=TD
(cosz
)=[0,
2π
).There are a few more examples as follows:Example 2.3
We recall that Mittag-Leffler function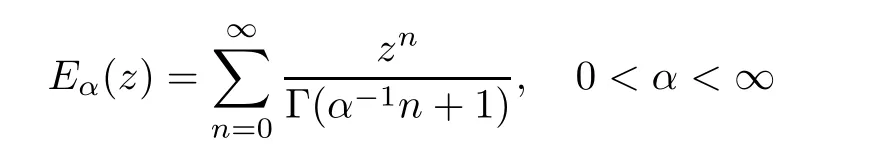
has the uniform asymptotic behavior[7,Chapter 1,(5.40)]
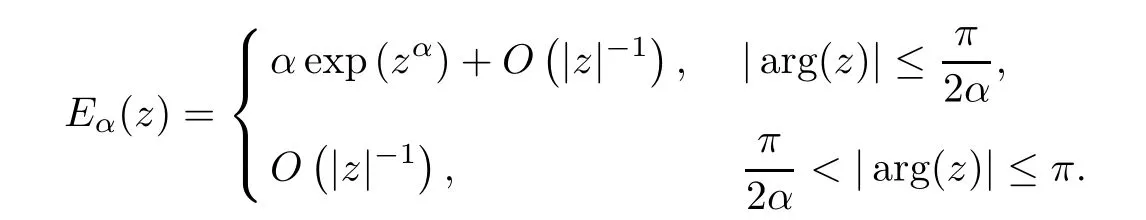
From this fact,it follows that
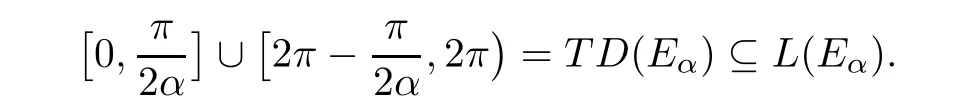
Example 2.4
From[19,(6.3.15)],the entire function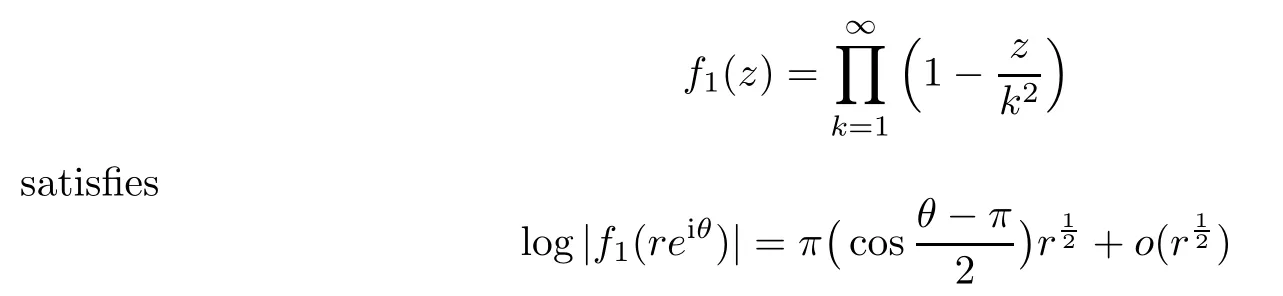
ε,
2π
?ε
)={z
:ε<
argz<
2π
?ε
}for every positive numberε
.Sinceε
is arbitrarily small,it is easy to see thatL
(f
)=TD
(f
)=[0,
2π
).Example 2.5
By[19,Lemma 7.9],for 1/
2<μ<
1,we know that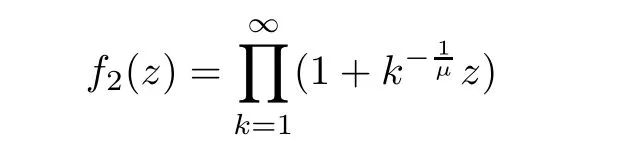
ε>
0,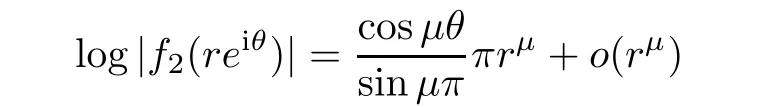
θ
for|θ
|<π
?ε.
This implies that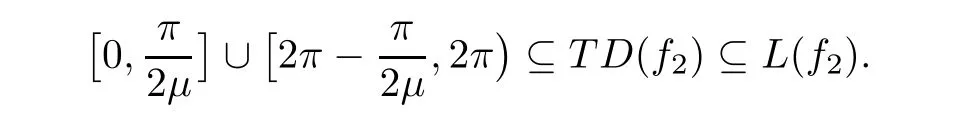
L
(f
),one possible way is to estimate the directions in whichf
grows quickly.To do this,we recall Baerstein’s result on the spread relation[1],which shows that forf
with not so many poles,log|f
|is‘large enough’on a substantial portion of circles{|z
|=r
}.Lemma 2.6
([1])Letf
be a transcendental meromorphic function with finite lower orderμ
and positive de ficiency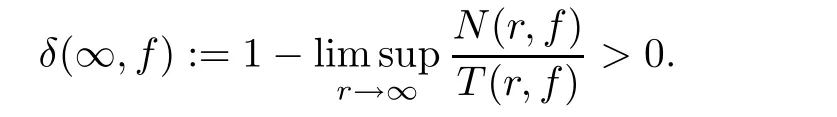
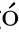
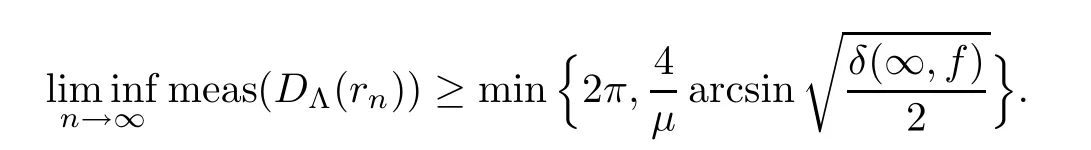
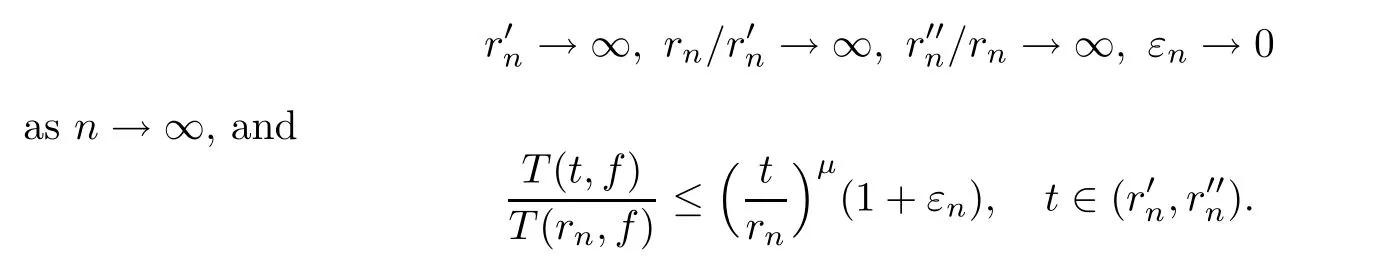
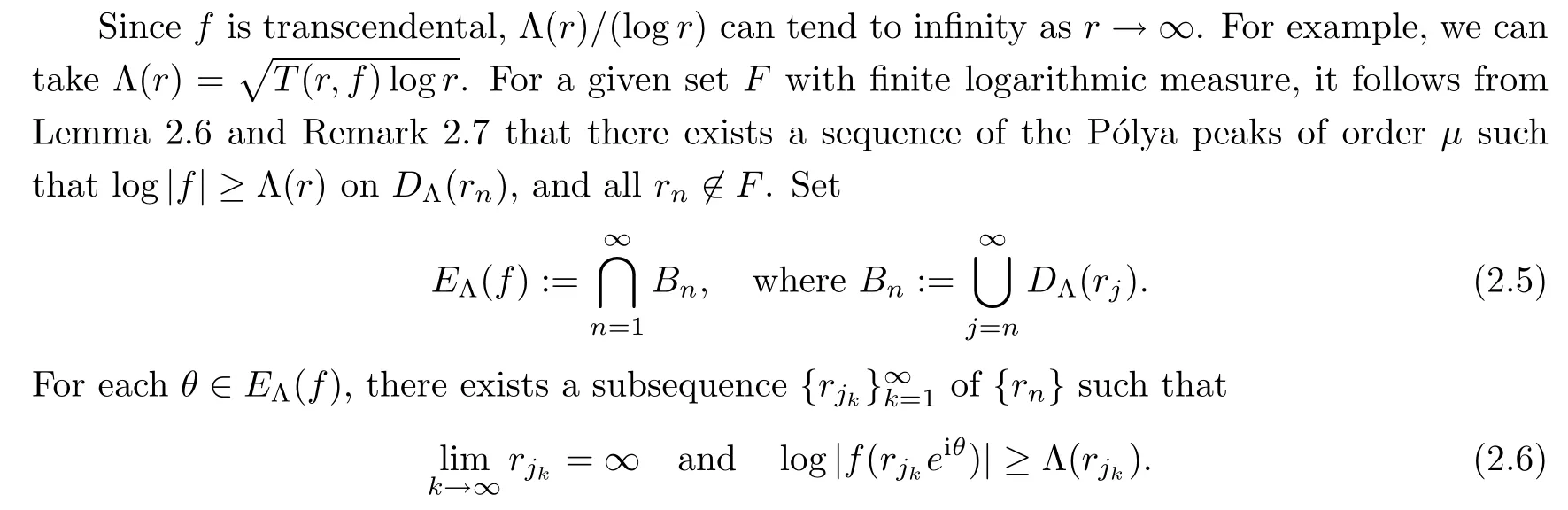
E
(f
)?TD
(f
),soE
(f
)?L
(f
),by Lemma 2.2.Next,by Lemma 2.6 and the monotone convergence theorem,we derive the lower bound of meas(L
(f
)).Lemma 2.8
Letf
be a transcendental meromorphic function with finite lower orderμ
andδ
(∞,f
)>
0,and let Λ(r
)be a positive function such that Λ(r
)=o
(T
(r,f
))and Λ(r
)/
(logr
)→∞asr
→∞.Then,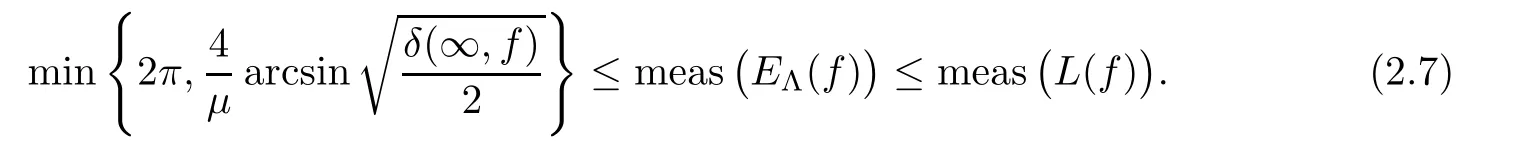
Proof It follows from Lemma 2.6 that
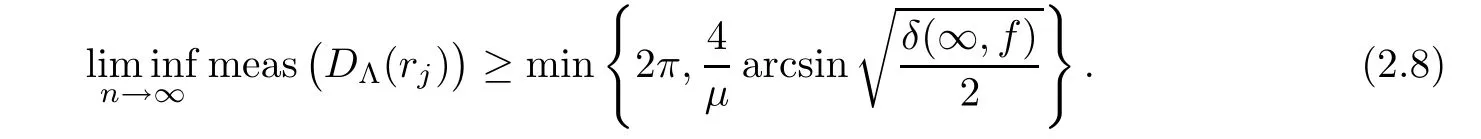
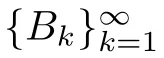
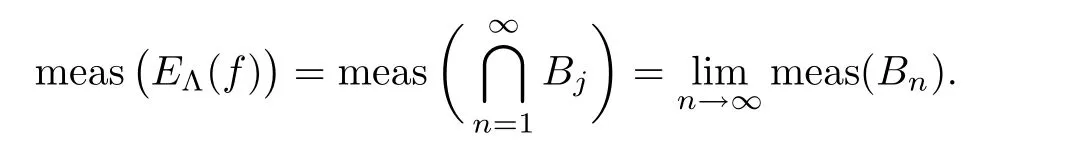
D
(r
)?B
for eachn
,we get that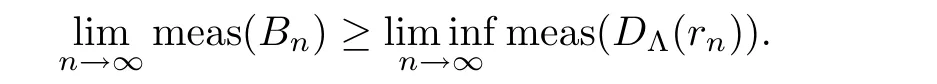
E
(f
)?L
(f
)yields inequality(2.7).In addition,we easily have the following lemma forL
(f
)∩L
(f
):Lemma 2.9
Letf
be a transcendental entire function,and letn
be a positive integer.ThenTD
(f
)?TD
(f
)andTD
(f
)?L
(f
)∩L
(f
).Proof
For any givenθ
/∈TD
(f
),it follows from the de finition of transcendental directions that there exist positive?
andK
such that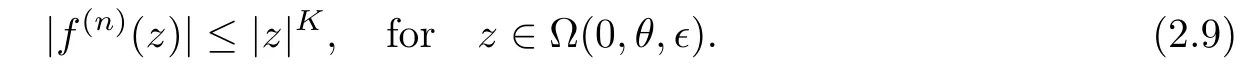
We note the fact that
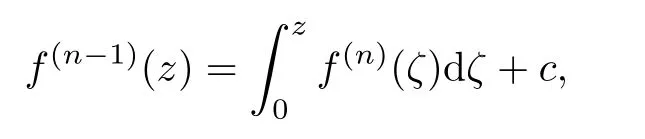
c
is a constant,and the integral path is the segment of a straight line from 0 andz
.From this and(2.9),it is easy to see that|f
(z
)|≤(K
+1)|z
|for allz
∈?(0,θ,?
).Repeating this discussionn
times yields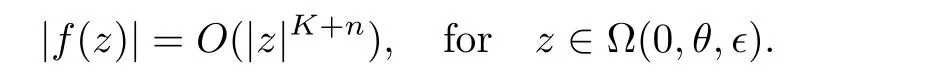
θ
/∈TD
(f
)ifθ
/∈TD
(f
),which implies thatTD
(f
)?TD
(f
).By Lemma 2.2,TD
(f
)?L
(f
)andTD
(f
)?L
(f
),soTD
(f
)?L
(f
)∩L
(f
).3 Proof of Theorem 1.3 and Some Examples
To prove Theorem 1.3,we still need the Nevanlinna theory in angular domains.For the convenience of the reader,we recall some basic de finitions here(for example see[7,22]).
Letg
(z
)be an entire function on the closure of ?(α,β
)={z
∈C:argz
∈(α,β
)},whereβ
?α
∈(0,
2π
].De fine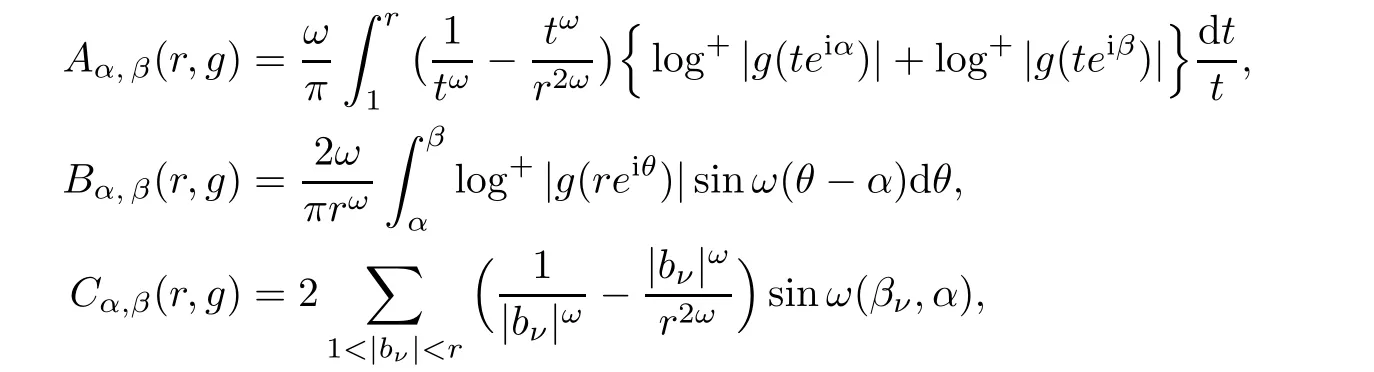
ω
=π/
(β
?α
)andb
=|b
|e
are the poles ofg
in the closure of ?(α,β
)appearing according to their multiplicities.Nevanlinna’s angular characteristic ofg
is de fined by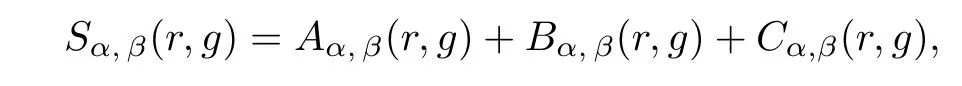
S
(r,g
)is de fined by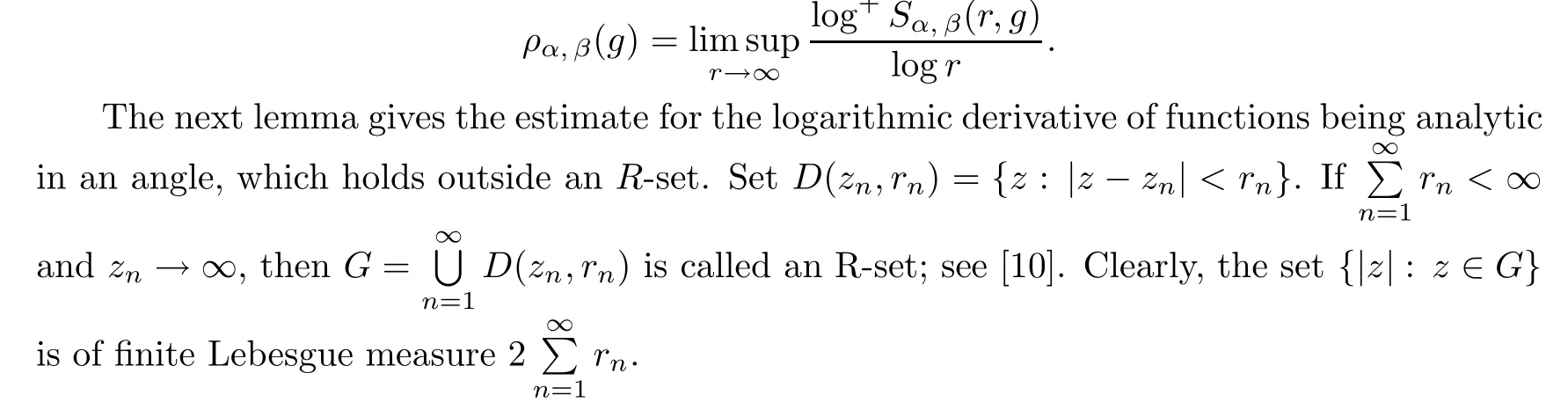
Lemma 3.1
([9,Lemma 2.2])Suppose thatn
∈N,and thatg
(z
)is analytic in ?(α,β
)withρ
(g
)<
∞.Then,forε
=0,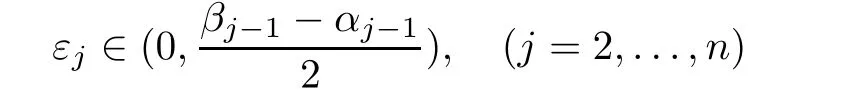
outside a set whose Lebesgue measure is zero,where
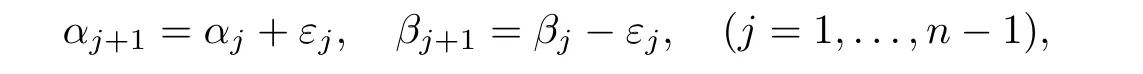
M,K
only depending ong,ε
,ε
,...,ε
,
?(α,β
)such that for allm
=1,
2,...,n
andz
=re
∈?(α
,β
),holds outside an R-set,wherek
=π/
(β
?α
)(j
=1,
2,...,n
).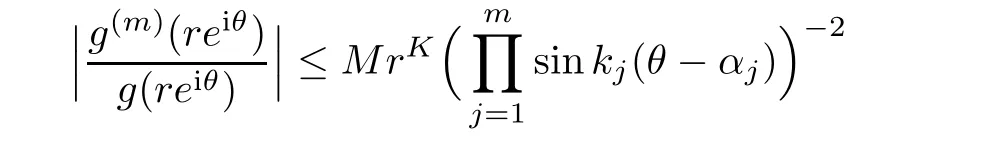
Lemma 3.2
([22,Theorem 2.5.1])Letf
(z
)be a meromorphic function on ?(α
?ε,β
+ε
)forε>
0 and 0<α<β<
2π
.Then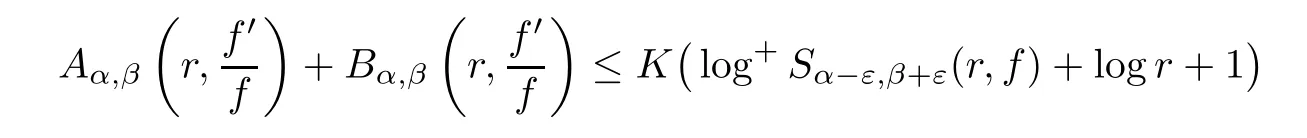
r>
1,possibly excepting a set with finite linear measure,and also we have the constantK>
0.Proof of Theorem 1.3
In what follows,we will treat three cases:n
=0,n>
0 andn<
0.Case 1.We assume thatn
=0.For everyθ
/∈TD
(f
),by the de finiti on of transcendental direction,there exist positive?
andK
such that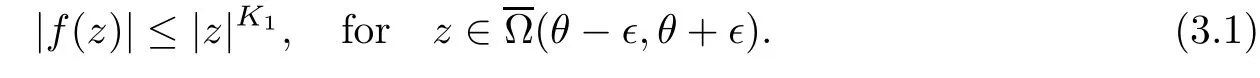
ρ
(f
)<
∞.By Lemma 3.1,there are positiveM
,K
and?
<?
such that
z
∈?(θ,?
)outside anR
-setG
,whereH
={r
=|z
|,z
∈G
}is a set of finite Lebesgue measure,andm
=1,
2,...,k
.We rewrite(1.6)as
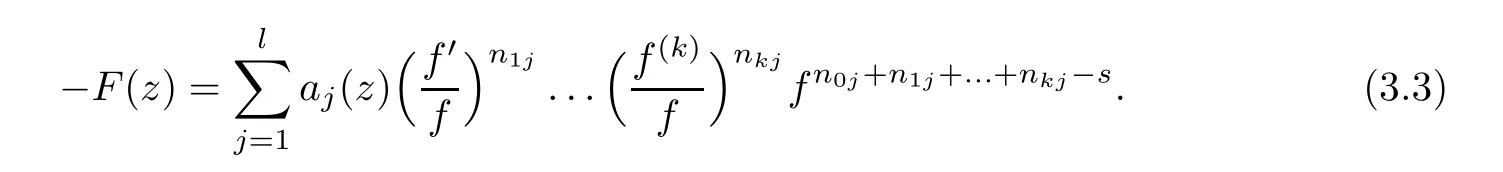
Taking(3.1)and(3.2)into(3.3)yields
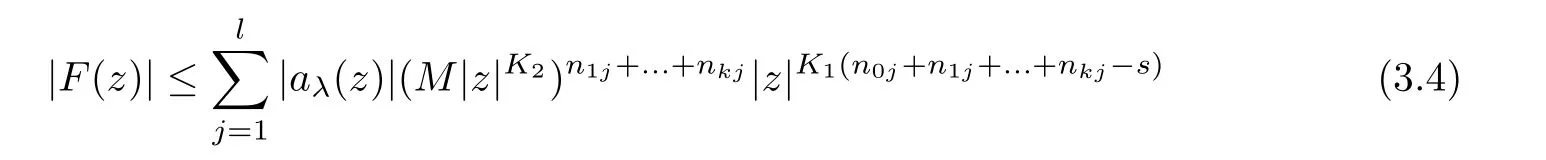
z
∈?(θ,?
)outsideG
,wheren
+n
+...
+n
?s
≥γ
?s
≥0.Whenμ
(F
)>
0,we take Λ(r
)=r
with
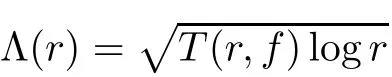
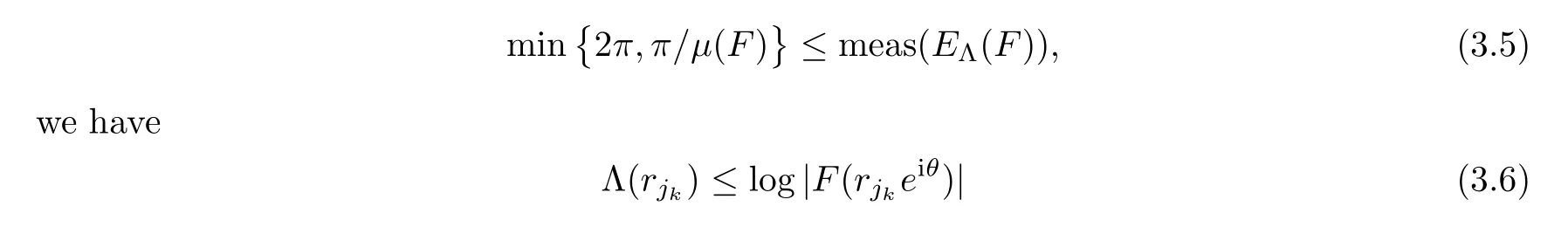
r
}of{r
}.For any given
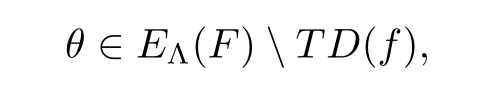
taking(3.6)into(3.4)yields
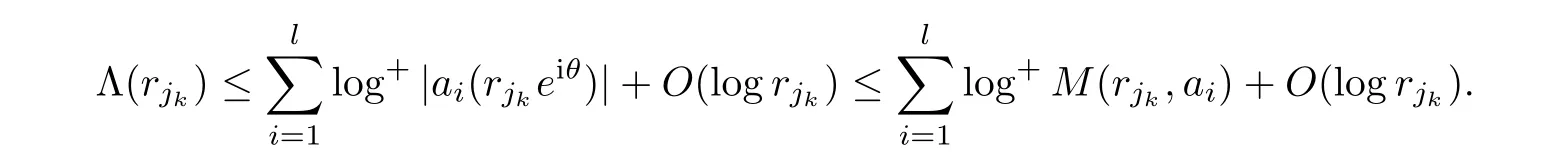
It follows from the de finition of order by maximum modulus that the above inequality implies that
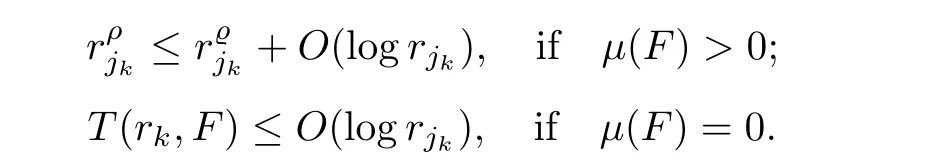
E
(F
)TD
(f
)=?,
so,by Lemma 2.2,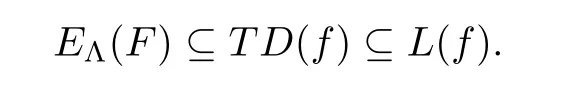
E
(F
)?TD
(F
).Therefore,we have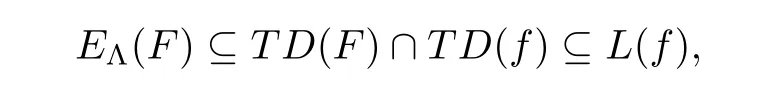
and(1.7)follows from(3.5).
Case 2.We assume thatn>
0.It follows from Lemma 2.9 thatTD
(F
)∩TD
(f
)?TD
(F
)∩TD
(f
),thus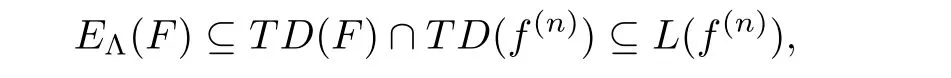
E
(F
)?TD
(f
),which similarly leads to(1.7).Case 3.We assume thatn<
0.Forθ
/∈TD
(f
),we know that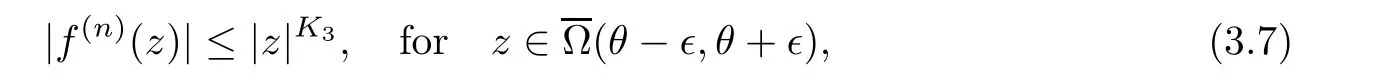
?>
0 andK
>
0.Thus,S
(r,f
)=O
(1),soρ
(f
)<
∞.Then,by Lemma 3.1,there are positiveM
,K
and?
<?
such that
z
∈?(θ,?
)outside anR
-setG
,whereH
={r
=|z
|,z
∈G
}is of finite Lebesgue measure.It follows from Lemma 3.2 that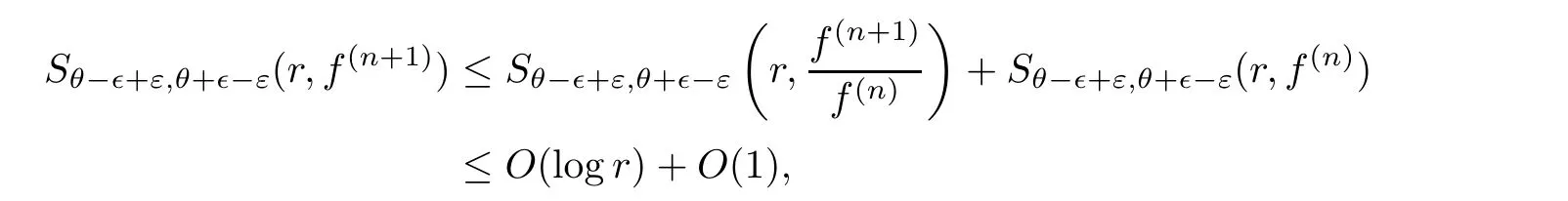
nε<?/
2.Repeating this discussionn
times yields that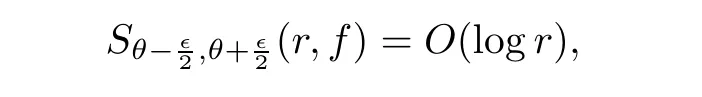
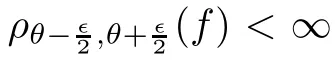
r
}such that allr
/∈H
∪H
,and forθ
∈E
(F
),we have(3.5)and(3.6),where Λ(r
)is de fined as in Case 1.We rewrite(1.6)as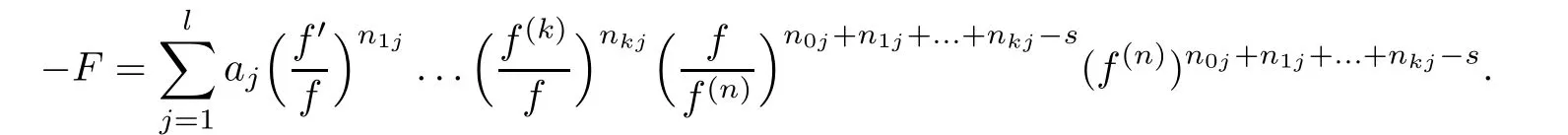
θ
∈E
(F
)TD
(f
),substituting(3.2),(3.6),(3.7)and(3.8)into the above equation yields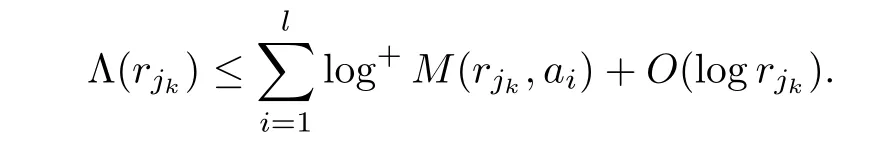
E
(F
)TD
(f
)=?,so,by Lemma 2.2,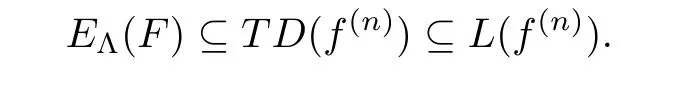
Therefore,we have
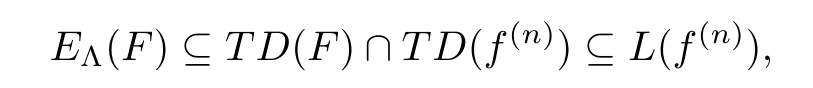
and(1.7)follows from(3.5)again.
This completes the proof of Theorem 1.3.
Remark 3.3
From the proof of Theorem 1.3,we know that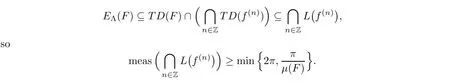
Finally,we give some examples for applications of Theorem 1.3.
Example 3.4
The solutions of the Mathieu differential equation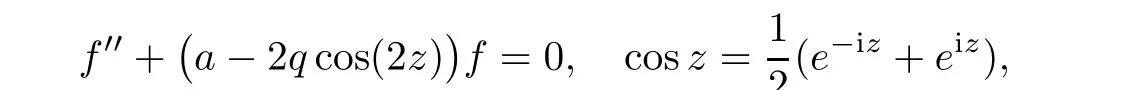
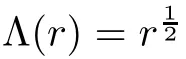
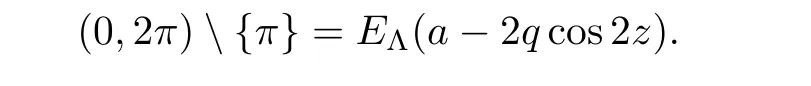
Since the set of transcendental directions is closed,we deduce that
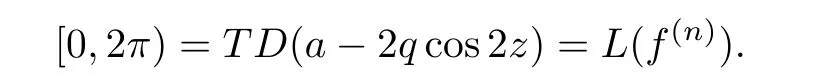
Example 3.5
Every non-zero solution of the equation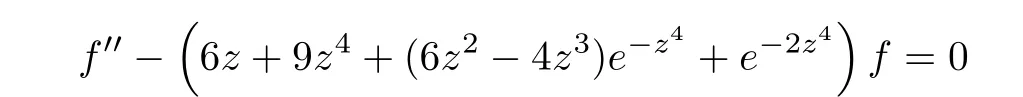
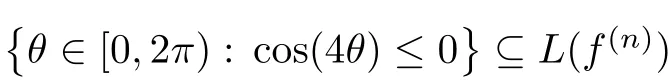

Example 3.7
Every entire solution of the equation satis fies[0,
2π
)=L
(f
),since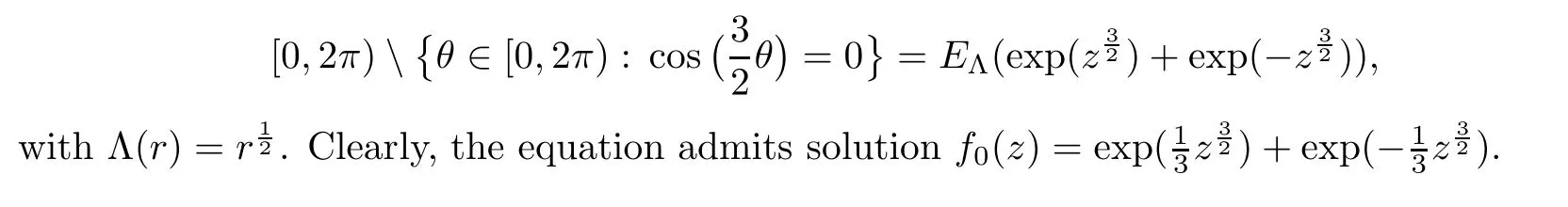
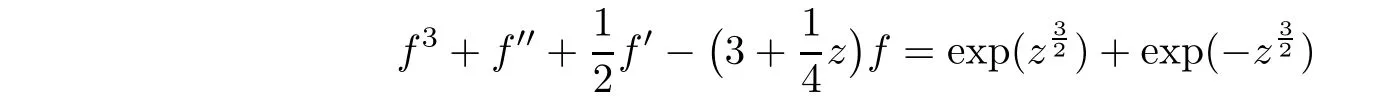
 Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY OF WEAK SOLUTIONS TO A CLASS OF NONLINEAR PROBLEM?
- EXISTENCE TO FRACTIONAL CRITICAL EQUATION WITH HARDY-LITTLEWOOD-SOBOLEV NONLINEARITIES?
- A DIFFUSIVE SVEIR EPIDEMIC MODEL WITH TIME DELAY AND GENERAL INCIDENCE?
- ON A COUPLED INTEGRO-DIFFERENTIAL SYSTEM INVOLVING MIXED FRACTIONAL DERIVATIVES AND INTEGRALS OF DIFFERENT ORDERS?
- CLASSIFICATION OF SOLUTIONS TO HIGHER FRACTIONAL ORDER SYSTEMS?
- ENERGY CONSERVATION FOR SOLUTIONS OF INCOMPRESSIBLE VISCOELASTIC FLUIDS?
