Asymptotic Behavior for A Class of Non-autonomous Nonclassical Parabolic Equations with Delay on Unbounded Domain
ZHANG Fang-hong, BAI Li-hong
(1.Regional Circular Economy key Laboratory of Gansu Higher Institutions, Lanzhou, China; 2.Department of Mathematics, Longqiao College of Lanzhou University of Finance and Economics, Lanzhou,China; 3.Department of Basic Courses, Gansu Institute of Architectural Technology, Lanzhou, China)
Abstract: In this article, we investigate the longtime behavior for the following nonautonomous nonclassical parabolic equations on unbounded domainUnder some suitable conditions on the delay term f and the non-autonomous forcing term g, we prove the existence of uniform attractors in Banach space CH1(RN) for the multivalued process generated by non-autonomous nonclassical parabolic equations with delays in unbounded domain.
Key words: Uniform attractors; Asymptotic behavior; Multi-valued process; Nonclassical parabolic equations with delay; Unbounded domain
§1. Introduction
One of the central problems in infinite dynamical systems is the investigate of the asymptotic behavior of evolution processes associated to the modeling of real world phenomena. If the model under study is an autonomous differential equation,the study of its asymptotic behavior is rather well established and many references on the subject are available (see, e.g. Babin and Vishik[4], Hale[8-9], Ladyzhenskaya[16], Temam[21], Robinson[28]and etc). If the evolution process comes from a non-autonomous differential equation, there exists a lot of works (see,e.g. Chepyzhov and Vishik [7], Kloeden and Rasmussen [12]), but it is a open field of study yet. The study of uniform attractors for infinite dimensional dynamical systems have attracted much attention and has made fast progress in recent decades, see, for instance, [4, 7-9, 16-17,20, 23, 25, 28]and the references therein.
In this paper, we investigate the asymptotic behavior of solutions to the following nonautonomous nonclassical parabolic equations with delays on unbounded domain RN
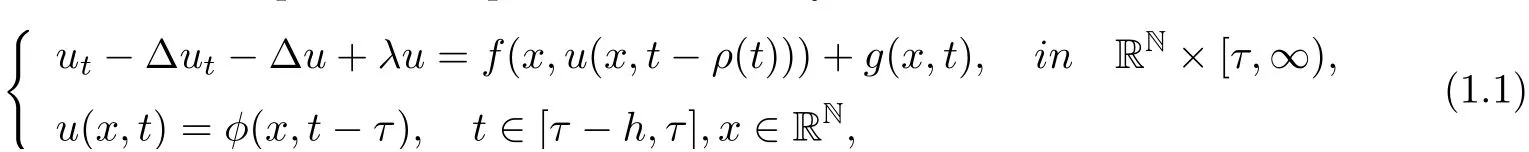
where λ>0, the nonlinearity f contains some memory effects during a fixed interval of time of length h > 0, ρ being an adequate given delay function, φ ∈C((?h,0];H1(RN)) is the initial data, and the time-dependent external force term g(x,t)∈
Let X be a Banach space with norm, let h > 0 be a given positive number, which will denote the delay time, and we denote by CXa Banach space C((?h,0];X) with the norm

Given T > τ and u : [τ ?h,T) →X, for each t ∈[τ,T) we denote by utthe function defined on [?h,0]by the relation ut(s)=u(t+s),s ∈[?h,0].
Nonclassical parabolic equations arise as models to describe physical phenomena such as non-Newtonian flow, soil mechanics, heat conduction, etc. (see Aifantis [1-2]; Kuttler and Aifantis [13-14]and references therein).
For the case without the variable delay, the long-time behavior, especially the uniform attractor and pullback attractor have been discussed by many authors,both in bounded domain and unbounded domain, e.g. see [3, 20, 29-30]and the references therein.
For the non-autonomous semi-linear nonclassical parabolic equations with delay in bounded domain, Caraballo and M′arquez-Dur′an [6]have obtained the existence and the uniqueness of solutions for the following functional differential equations

In[10,32],the existence of pullback attractors for the following nonclassical diffusion equations with delay
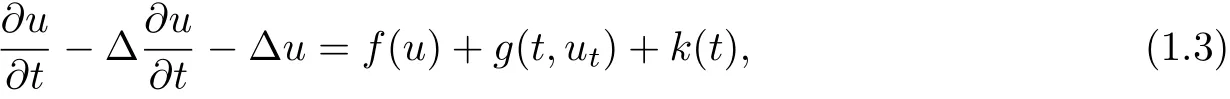
is treated when the nonlinearity satisfying critical exponent and polynomial growth of arbitrary order respectively.
Thanh and Toan [22]proved the existence of a pullback D-attractor for the following nonclassical diffusion equations with polynomial nonlinearity and infinite delay in bounded domains.
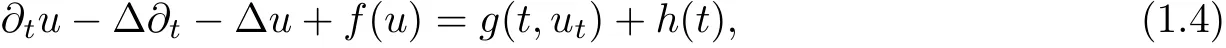
Zhang and Bai [31]obtained the existence of pullback attractors for multi-valued process generated by non-autonomous nonclassical parabolic equations
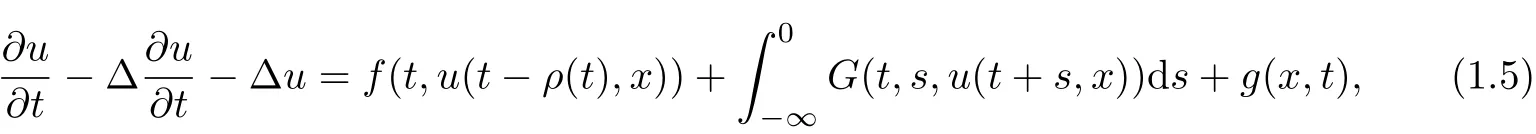
with unbounded delays without uniqueness of solutions in the weighted space
To our best knowledge, the existence of uniform attractors for Equ.(1.1) in unbounded domain has not been considered by predecessors. There are some difficulties in establishing the existence of uniform attractors. On the one hand, some method used in [7-9, 15-16, 28]cannot be directly employed in our case since the Sobolev embeddings are no longer compact. On the other hand, it is worth noticing that Equ.(1.1) contains the term ??ut, this is essentially different from the classical reaction diffusion equation in[5,7-8,16,21,24,26-27]. For example,the reaction diffusion equation has some kind of”regularity”;e.g.,although the initial data only belongs to a weaker topology space, the solution will belong to a stronger topology space with higher regularity. However,for Equ. (1.1),because of the term ??ut,the solution has no higher regularity,i.e.,if the initial data φ(x,t?τ)only belongs to CH1(RN),then the solution is always in CH1(RN)and has no higher regularity, which is similar to the hyperbolic PDEs. Thirdly, we do not assume the lipschtiz conditions on the delay term, which is completely different from[10, 22, 32], in this case, the uniqueness of the weak solutions is lost. Fourth, the delay term f(x,u(x,t ?ρ(t))) also cause some difficulties to obtain the existence of uniform attractors.
This paper is organized as following: In Section 1, we have expounded on research progress with regard to our research problem, and introduce some notations and functions spaces. In Section 2,for convenience of the reader,we present some useful lemmas and associated theories which will be used later. In Section 3, we prove the existence of uniform attractor in CH1(RN).
§2. Preliminaries
In this section, we recall some notations about the function spaces,some definitions and basic results concerning the uniform attractor, which is necessary to obtain our main results,please refer the reader to [4, 7-8, 11-12, 16-17, 23-25]for more details.
Let X be a complete metric space with metric dX(·,·),and let P(X)be the class of nonempty subsets of X. Denote bythe Hausdorff semidistance between two nonempty subsets of a complete metric space X, which are defined by
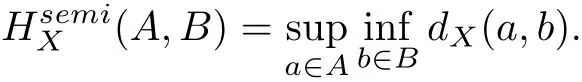
We denote by N(A,r) the open neighborhood {y ∈X | distX(y,A) < r} of radius r > 0 of a subset A of a complete metric space X.
Let (Σ;dΣ) be a complete metric space. Σ will denote the symbol space underlying the dynamics.
Definition 2.1A family of mappings Uσ(t,τ):X →P(X), t ≥τ, τ ∈R, is called to be a multi-valued process with σ ∈Σ if
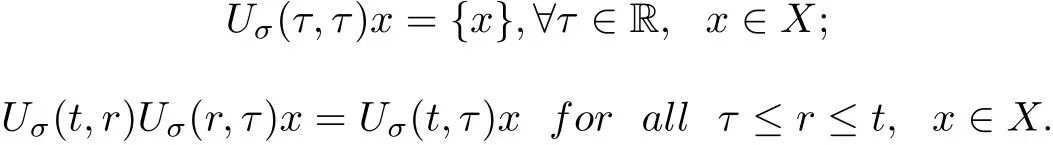
It is said to satisfy a translation identity with respect to a continuous semigroup {T(h)}h∈R+of Σ onto itself if
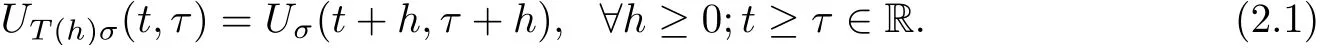
Definition 2.2A compact set A ?X is called the uniform attractor of the family of multi-valued processes {Uσ(t,τ)}σ∈Σif
(1) A uniformly attracts every bounded subset B of X, i.e., for any fixed τ ∈R,
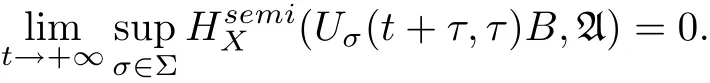
(2) for another compact setsatisfying (2.1), then
The Kuratowski measure k(A) of noncompactness of set A is defined by k(A)=inf{δ >0|A admits a finite cover by sets whose diameter ≤δ}.
The weak sequential closureof a subset A of a Banach space X is defined by={x ∈X |?{xn}?A, s.t., that is, xnconverges weakly to x}.
Theorem 2.3Let{Uσ(t,τ)}σ∈Σbe a family of multi-valued processes on a Banach space X satisfying the translation identity (2.1). Then the following statements are equivalent:
(1) {Uσ(t,τ)}σ∈Σis uniformly dissipative, i.e., for any fixed τ ∈R, there exists a bounded subset V of X so that for any bounded set B ?X, there exists a T0= T0(B,τ) ∈R+,independent of σ ∈Σ, such that
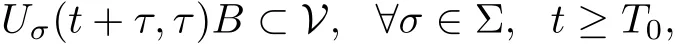
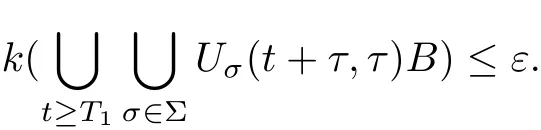
(2) {Uσ(t,τ)}σ∈Σhas a unique uniform attractor A=ω0,Σ(V)=ωτ,Σ(V) for τ ∈R, where
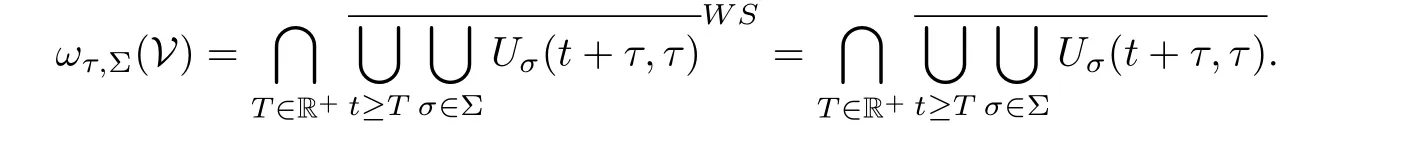
The following theorem will be used to verify that the multi-valued process {U(t,τ)} on CXis uniformly ω-limit compact.
Theorem 2.4Let{Uσ(t,τ)}σ∈Σbe a multi-valued process on CX. Suppose that for each τ ∈R, every bounded subset B of CXand any ε>0, there exist T =TB,τ,ε∈R+, independent of σ ∈Σ, a finite-dimensional subspace Xεof X and a δ >0 such that
(1) for each fixed θ ∈[?h,0],
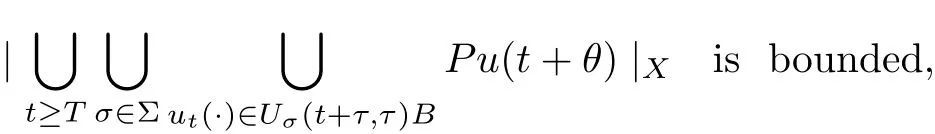
(2) for all t ≥T, σ ∈Σ, ut(·)∈Uσ(t+τ,τ)B, θ1,θ2∈[?h,0]with |θ2?θ1|<δ,|P(u(t+θ1)?u(t+θ2))|X<ε,
(3) for all t ≥T, σ ∈Σ, ut(·)∈Uσ(t+τ,τ)B,
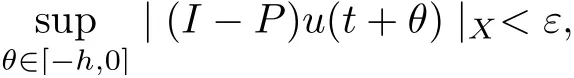
where P :X →Xεis the canonical projector. Then{Uσ(t,τ)}σ∈Σis uniformly ω-limit compact in CX.

Definition 2.5Let X be a Banach space. A function ? ∈(R,X) is said to satisfy Condition (C?) if for any ε>0, there exists a final dimensional subspace X1of X such that
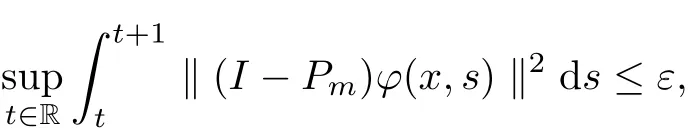
where Pm:X →X1is the canonical projector.
Let X be a Banach space, and denote byR,X) the set of all function satisfying Condition (C?).
Theorem 2.6If ?R,X), then for any ε>0 and τ ∈R, we have
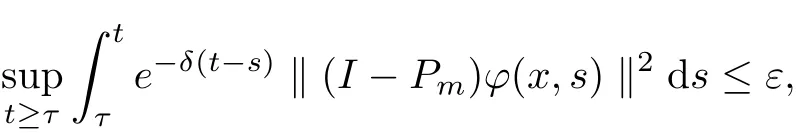
where Pm:X →X1is the canonical projector, and δ >0.
Theorem 2.7Let X be a Banach space,then(R,X)is a closed subspace of(R,X).
Let g0∈(R;L2(RN)), according to Theorem 2.7, g0∈;L2(RN)), and define the hull H(g0) of g0to be the closure of the {g0(τ +·):τ ∈R} in(R;L2(RN)).
Theorem 2.8For all
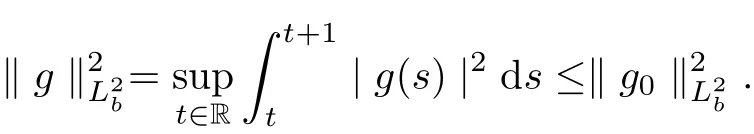
Let us recall the following facts, which can be founded in V. V. Chepyzhov and M.I. Vishik[7].
Definition 2.9Let X be a Banach space. A function ?(s) is translation bounded in(R,X), i.e.,
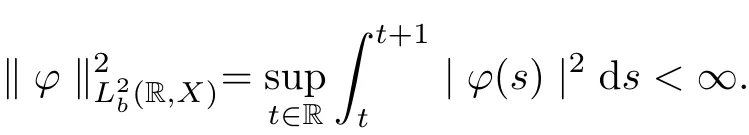
Theorem 2.10Let X be a Banach space. A function ?(s) is translationcompact in(R,X) if and only if
§3. Attractors in CH1(RN)
We investigate the following non-autonomous nonclassical parabolic equations on unbounded domain RN
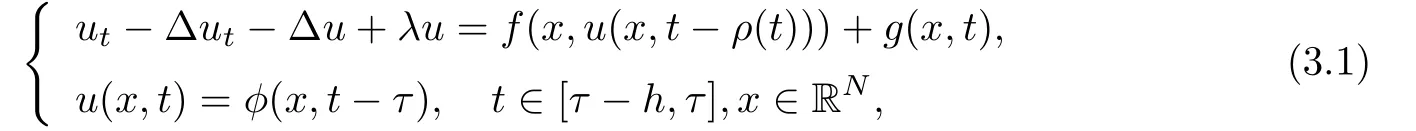
where λ>0, φ ∈C((?h,0];H1(RN)) is the initial data, and the time-dependent external force term g(x,t)∈L2C?(R,L2(RN)).
For the nonlinear function,assume that f ∈C(RN×R;R)satisfy the following assumptions:there exist a positive constant m2, a positive scalar function m1∈L2(RN) and a smooth function ρ ∈C(R;[0,h]) satisfy
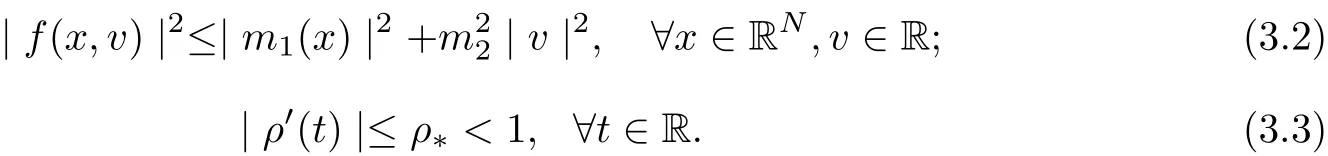
With the usual notation, hereafter let |u| be the modular (or absolute value) of u,be the norm of L2(RN),be the norm of H1(RN) = V, In the sequel C denotes an arbitrary positive constant, which may be different from line to line and even in the same line.
3.1 Existence of solutionsWe will give the following general existence of solutions for Equ. (3.1) which can be obtained by the standard Faedo-Galerkin method (see [4, 6-8, 13, 16,21-22,28]). Some techniques about the delays can be founded in[5-6,18-19]and the unbounded case can be founded in [3, 24-25, 27, 29]. Here we only formulate the result:
Theorem 3.1Assume that (3.2)-(3.3) hold, g(x,t) ∈L2C?(R,L2(RN)), φ ∈CH1(RN).Then, for each τ ∈R, there is a solution u(t) of Equ. (3.1) such that

Thanks to Theorem 3.1, we can define a family of multi-valued process{Ug(t,τ)}g∈H(g0)on CH1(RN)corresponding to Equ. (3.1) by

3.2 Existence of uniformly absorbing setsThe following estimate will be used to obtain the uniformly dissipative of multi-valued process {Ug(t,τ)}g∈H(g0).
Lemma 3.2Under the assumptions of lemma 3.1, and
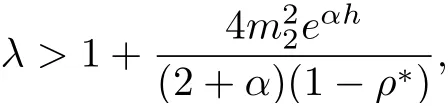
then all solutions of Equ. (3.1) satisfy
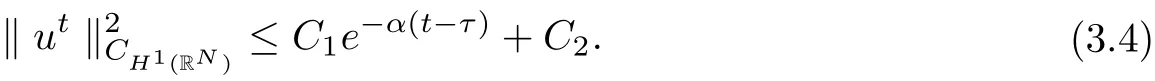
where λ is a large positive constant, 0 < α < 1, C1is dependent on, λ, α, h,and ρ?, and C2is dependent on, α, h, and ρ?.
ProofMultiplying (3.1) by u+ut, we infer
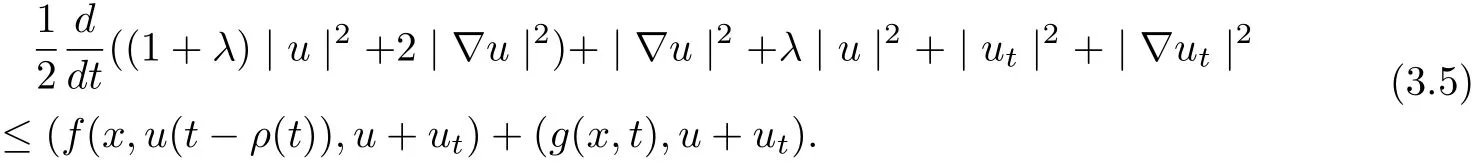
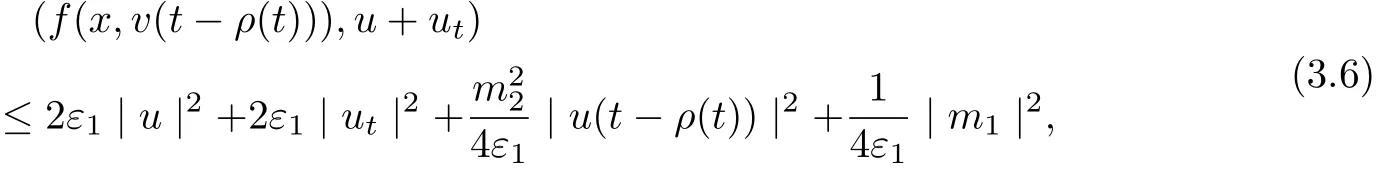
and
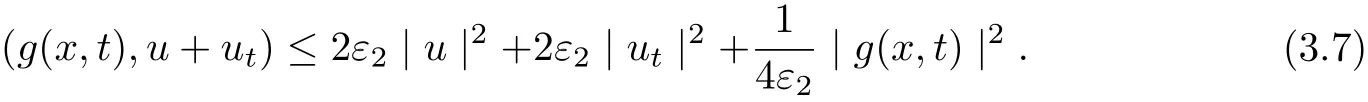
It follows from (3.5)-(3.7) that
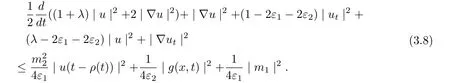
Multiplying (3.8) by eαt(0<α<1), we infer
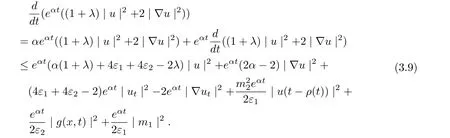
Noting that α<1, now integrating (3.9) from τ to t, thus
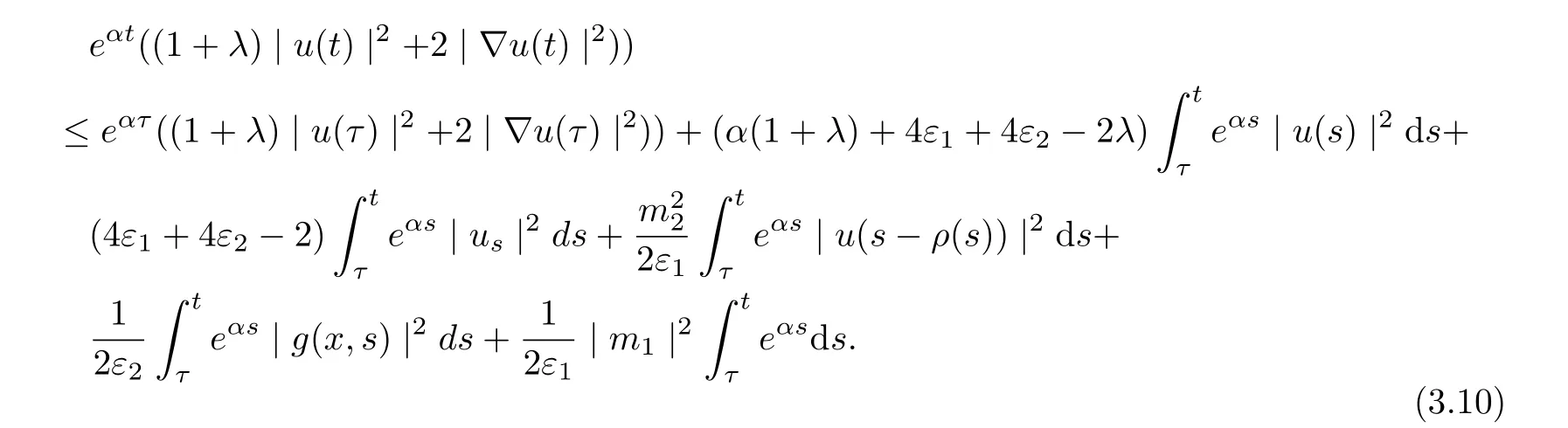
Noting that ρ(s) ∈[0,h]and the factfor all s ∈R. Setting v = s ?ρ(s), we arrive at
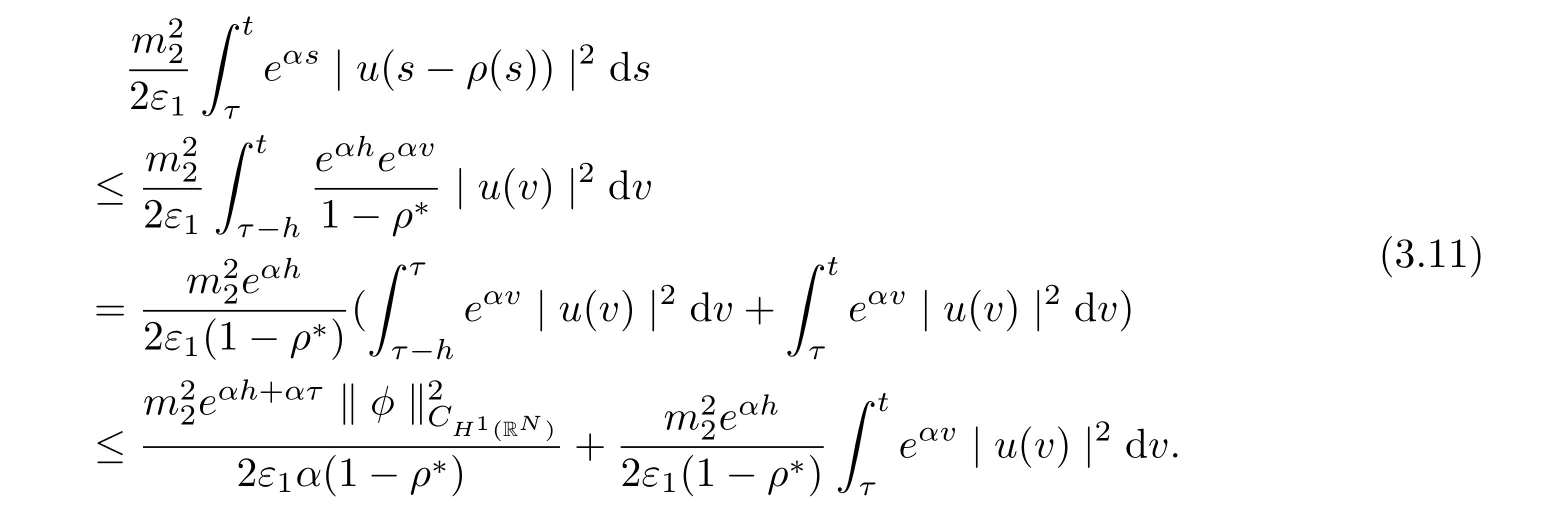
It follows from (3.10)-(3.11) that
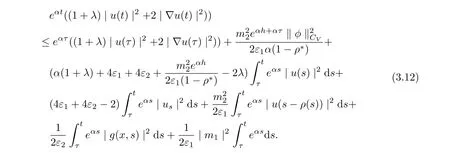
Choosing ε1=ε2=and noting that
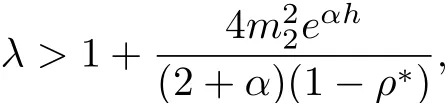
then
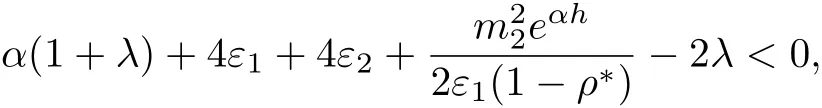
and
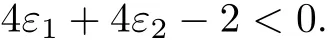
Thus,
Setting t+θ instead of t, where θ ∈[?h,0]. Multiplying by e?αt?αθ, we infer
Hence, we obtain
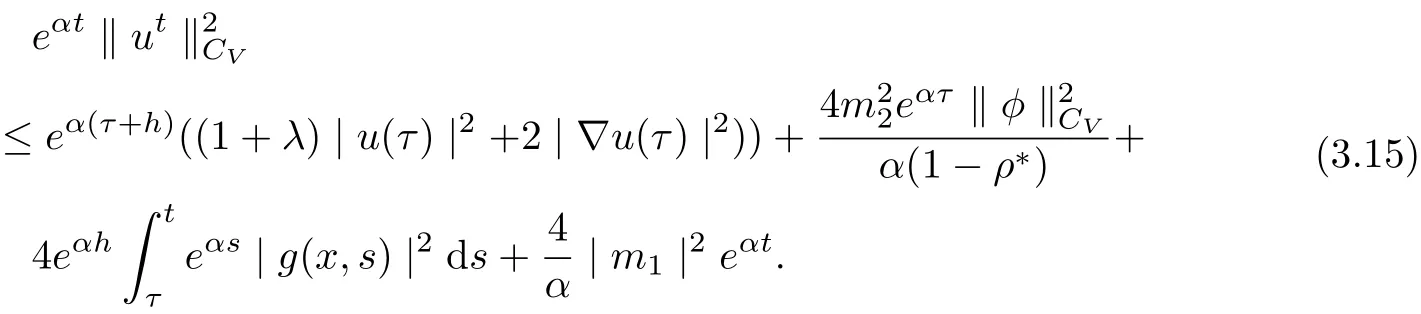
Then
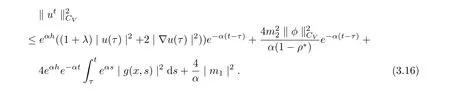
Using Theorem 2.8, we have
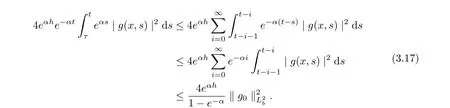
It follows from (3.16)-(3.17) that
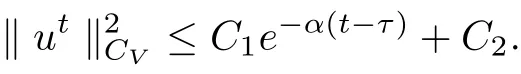
where
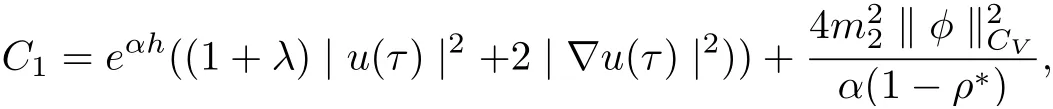
and
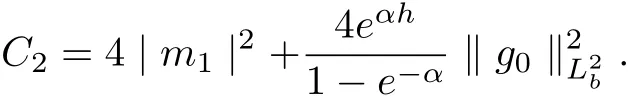
This complete the proof.
According to Lemma 3.2,it is straightforward to see that the multi-valued process{Uσ(t,τ)}g∈H(g0)is uniformly dissipative in CV.
3.3 Estimates on the exterior of a ballThe following lemma is crucial to estimate on the exterior of a ball.
Lemma 3.3Under the assumptions of Lemma 3.2, then ut(t) satisfies

where C3is dependent onλ, h, and ρ?, and C4is dependent on
ProofFrom Equ.(3.12), choosing ε1, ε2and λ as in lemma 3.2, we have
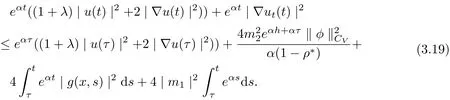
Similar to (3.17), we have

Then, we infer
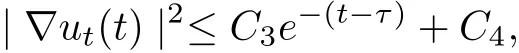
where

and
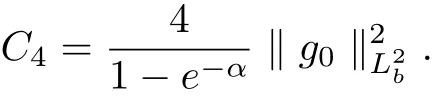
We now establish the following skillfull estimates,and these estimates are crucial for proving the uniformlycompact.
Lemma 3.4Under the assumptions of Lemma 3.2,then for anyand every bounded set B ?CV, there exist K >0 and T >0 such that
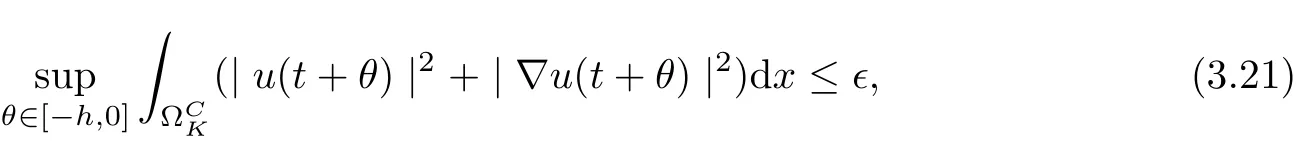
?t ≥T, g ∈H(g0), φ ∈B,ut(·)∈Ug(t,τ)φ, and ?CK={x ∈RN||x|≥K}.
ProofChoose a smooth function θ(x) with

where 0 ≤θ(s)≤1,s ∈R+, and there is a constant c such that |s)|≤c for s ∈R+.
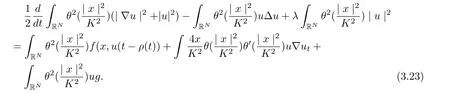
Next, we bound each term in (3.23) one by one as follows
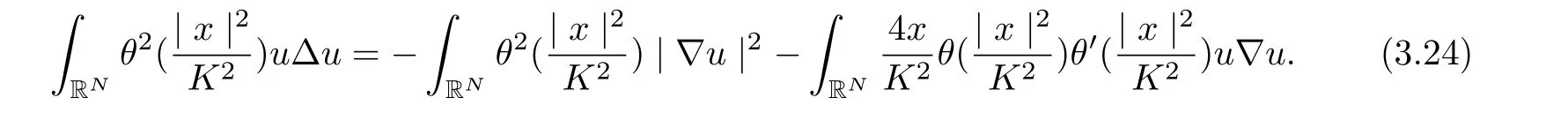
and by Lemma 3.2, we get
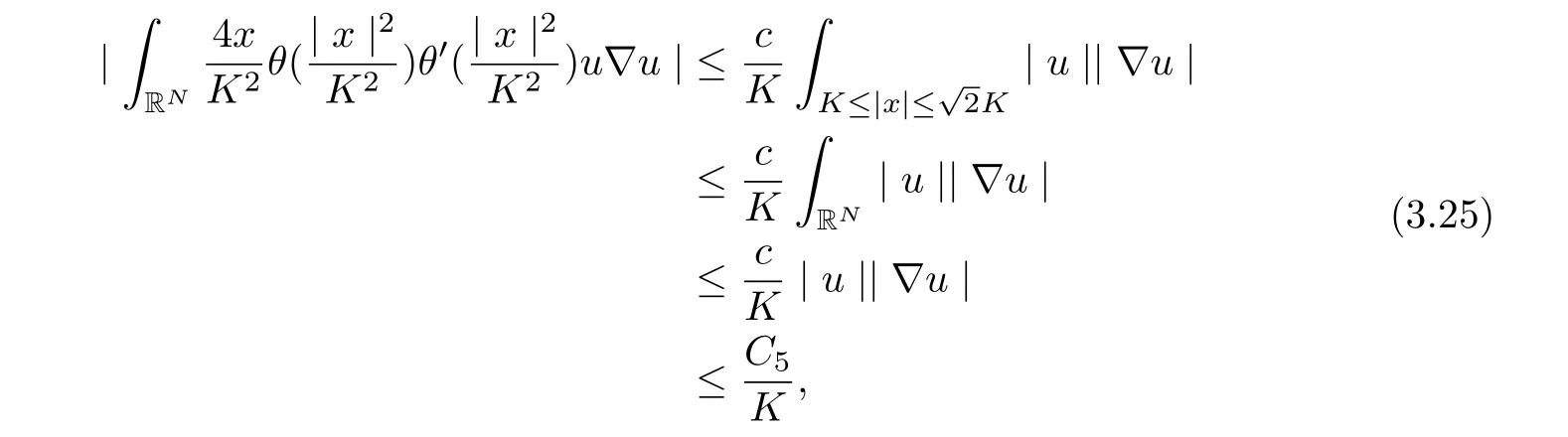
for all t ≥τ +1, where C5is dependent onλ, α, and ρ?.
Using Lemma 3.2 and Lemma 3.3, we infer
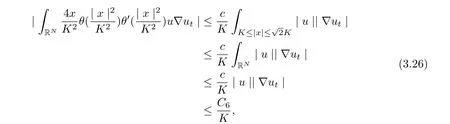
for all t ≥τ +1, where C6is dependent on, λ, α, and ρ?.
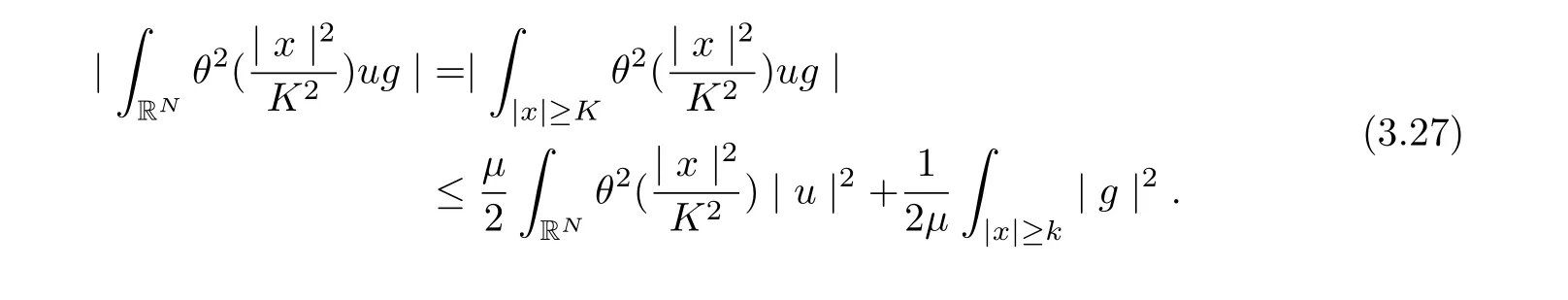
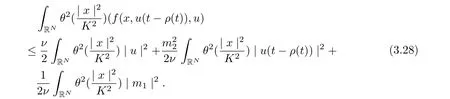
It follows from (3.23)-(3.28) that
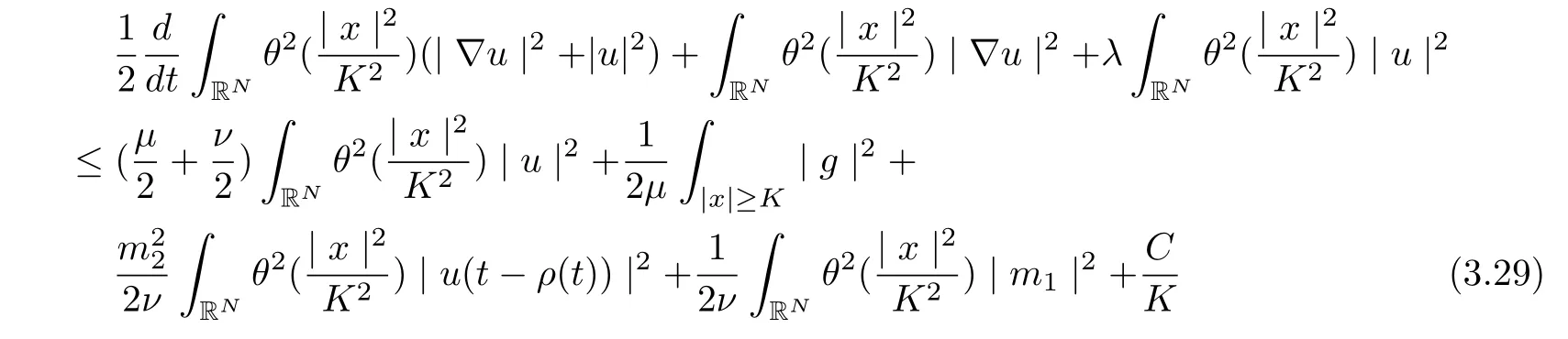
for all t ≥τ +1.
Thus
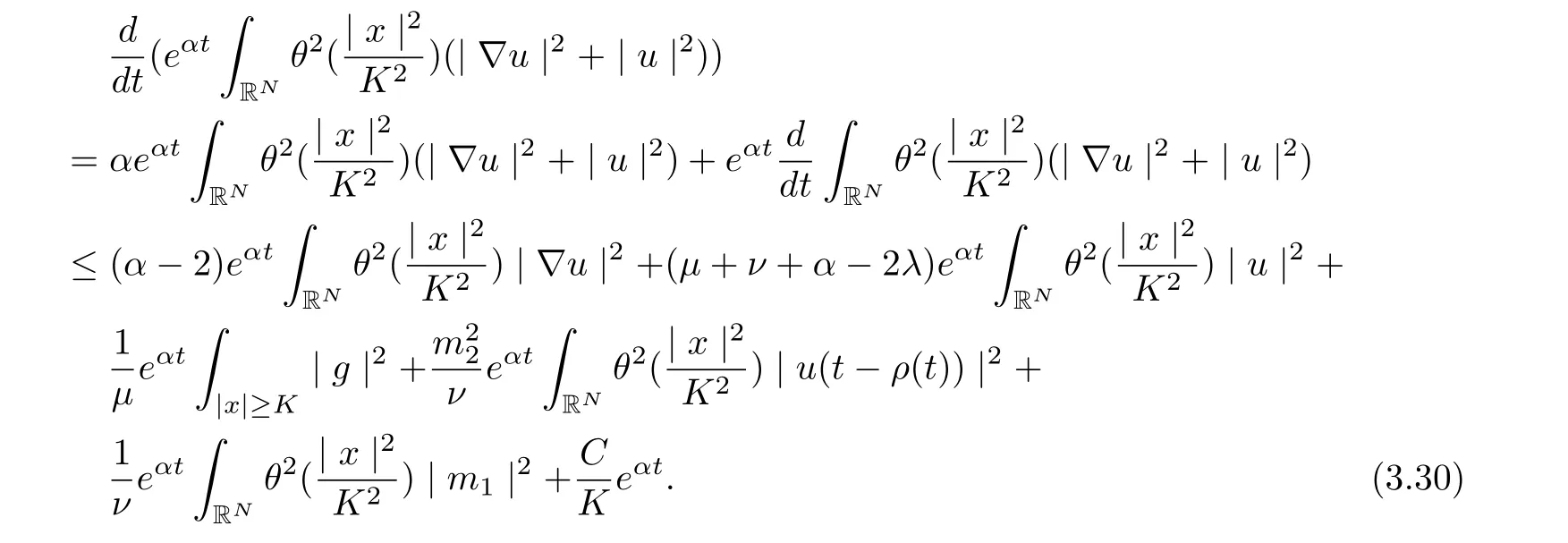
Integrating from τ to t with t ≥τ +1, and note that α<1, we infer
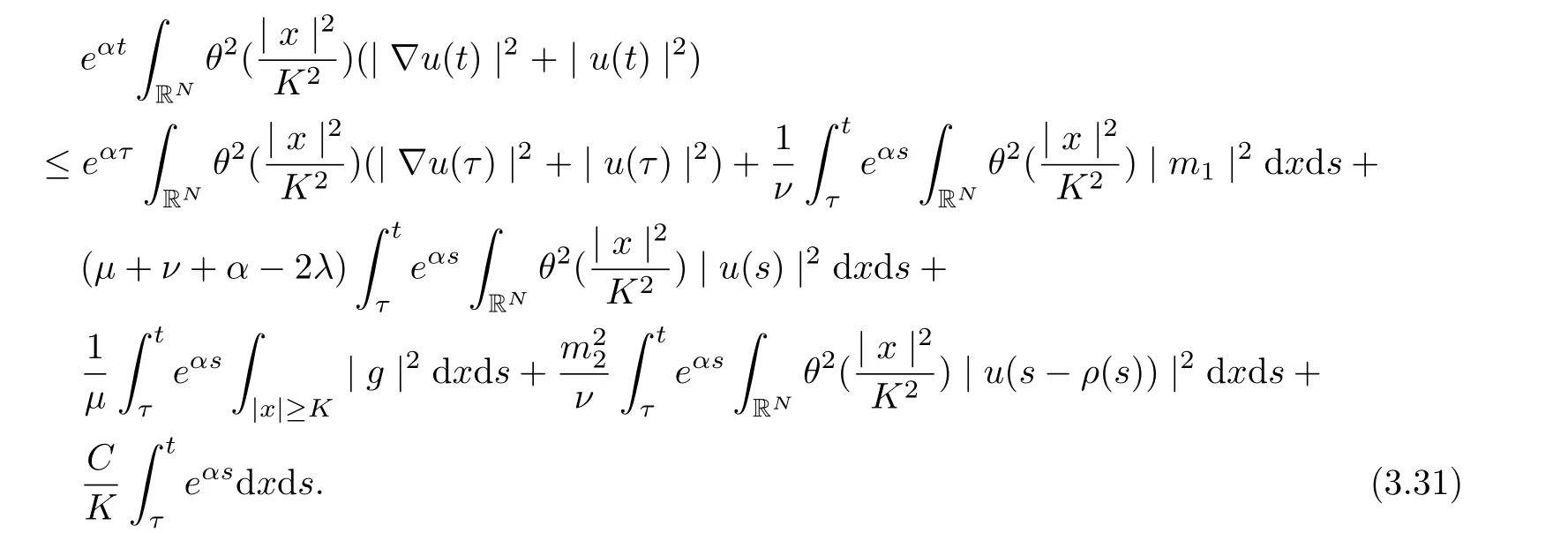
Noting that ρ(s) ∈[0,h]and the factfor all s ∈R. Setting v = s ?ρ(s), we infer
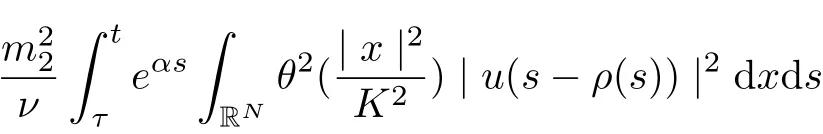
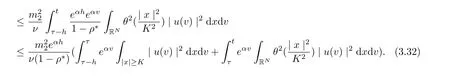
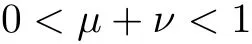
and
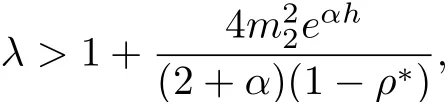
we arrive at
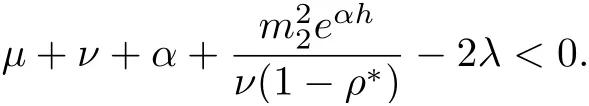
Thus, for t ≥τ +1, we get
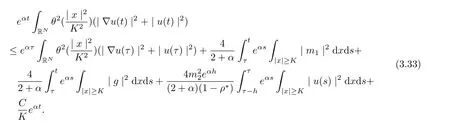
Replacing t by t+r, where r ∈[?h,0], and multiplying by e?α(t+r), for t ≥τ +1, we get that

Hence, for t ≥τ +1, we infer
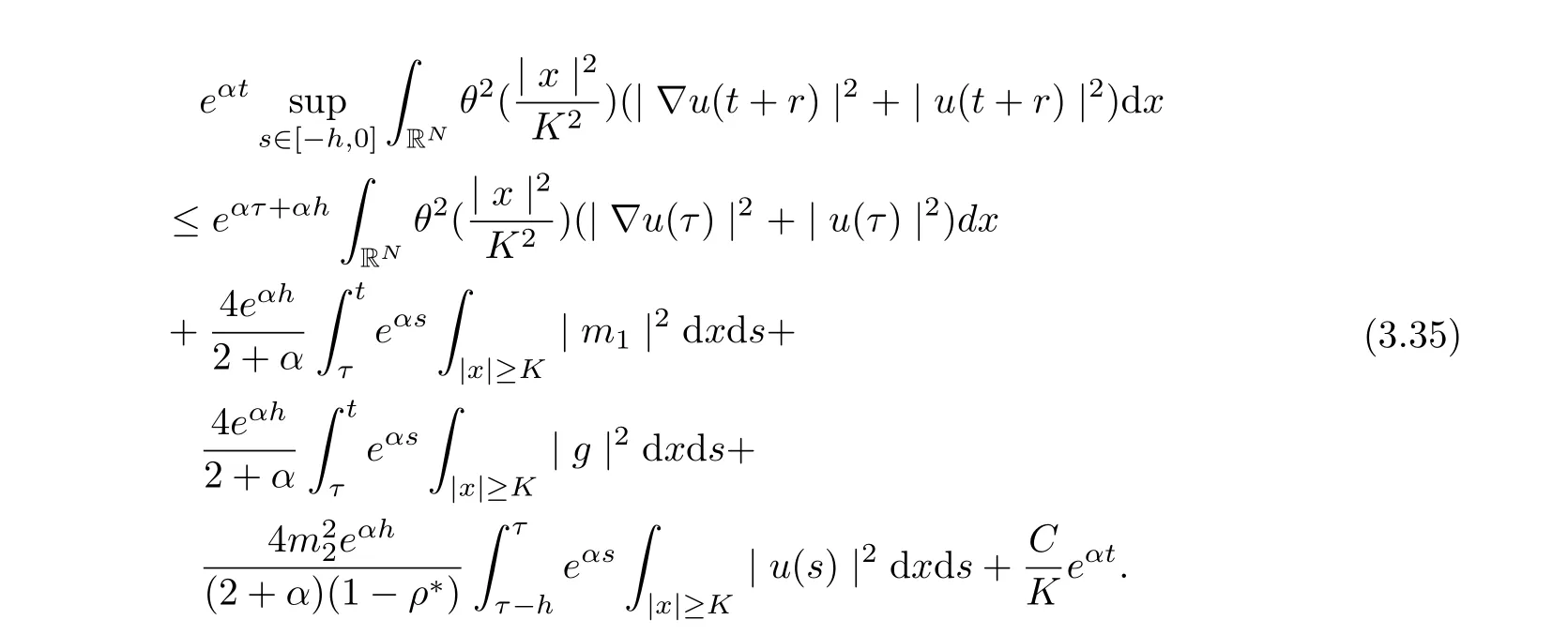
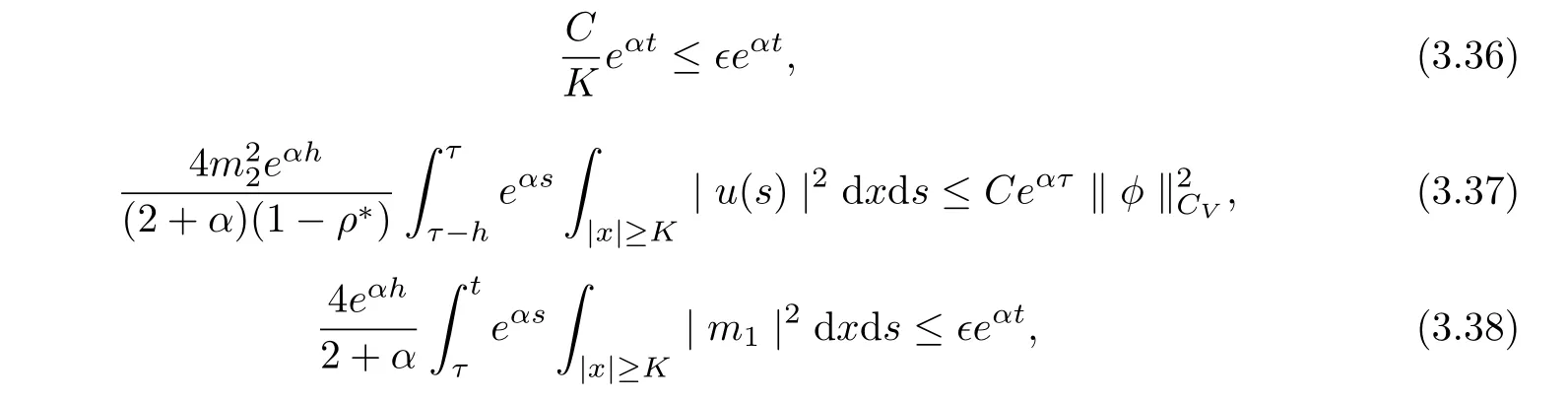
and
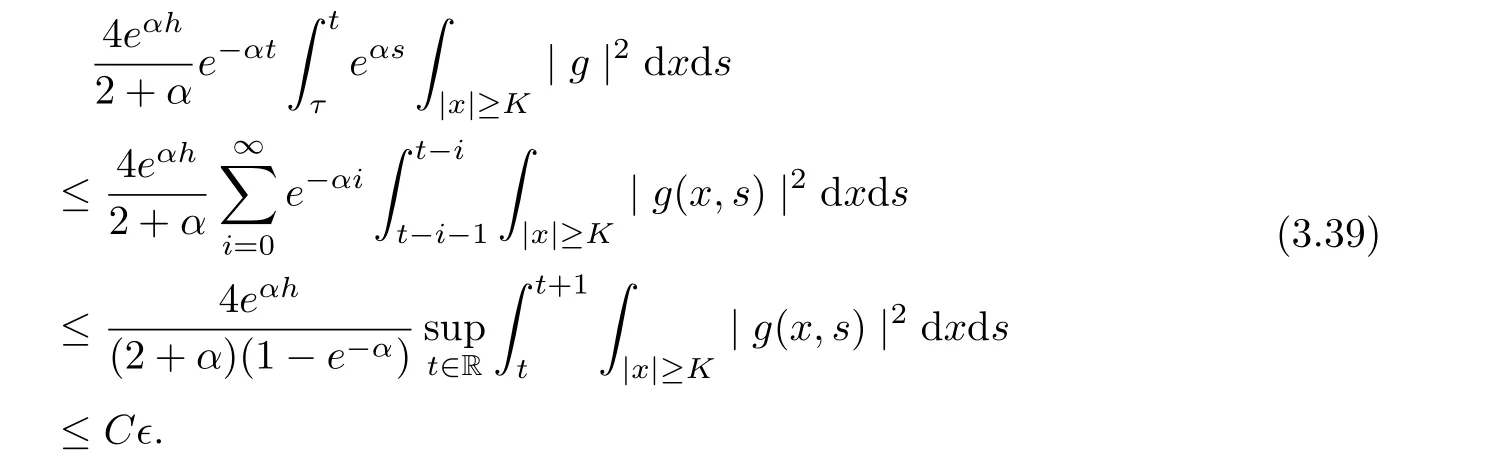
Hence, we infer
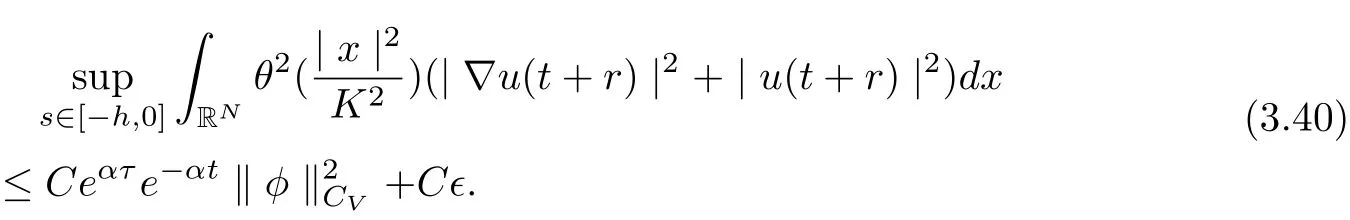
Now, we can take t large enough such that

This complete the proof.
3.4 Uniform attractors inCVWe denote ?K=| and We decompose Equ. (3.1) as follows: where v(x,t)=u(x,t)χ?Kand w(x,t)=u(x,t)χC?Ksatisfying the following equations, respectively: and According to Theorem 3.1, there exists a solution v(t) to problem (3.41), and Equ. (3.42)has a solution w(t):=u(t)?v(t). Lemma 3.5 Under the assumptions of Lemma 3.2, for any fixedanyand every bounded subset B ?CV,there exist T >0 and a finite-dimensional subspace P)ofand δ >0 such that (1) for all t ≥T +τ, g ∈H(g0), ut(·)∈Ug(t+τ,τ)B, θ1,θ2∈[?h,0]with |θ2?θ1|<δ, (2) for all t ≥T +τ, g ∈H(g0), ut(·)∈Ug(t+τ,τ)B, Proof We consider the operator A = ??with Dirichlet boundary conditions. Since A is self-adjoint, positive operator and has a compact inverse, there exists a complete set of eigenvectorsin L2(?K), the corresponding eigenvaluessatisfy We set Vm=span{ω1,ω2,...,ωm}. Pmis the orthogonal projection onto Vm,and Qm=I ?Pmis the orthogonal projection onto the orthogonal complement of Vm, v =Pmv+Qmv =v1+v2.We decompose (3.41) as follows: and We divide the proof into two steps. Step 1: We consider the finite-dimensional functional differential system (3.41). Noting that |?v1|2≤λm|?v1|2≤λ2m|v1|2. Without loss of generality, we assume that θ1,θ2∈[?h,0]with 0<θ1?θ2<1. Then According to (3.2), for all t ≥τ, we get Using (1.2), we infer Noting that g ∈H(g0)?we have Now, it only remains to estimate the bound ofdT. Taking the inner product of (3.43) with v1, ??v1,and ??respectively, then we infer and Now, (3.49)+(3.50)?(3.51)?λ(3.52), usinginequality, we infer Noting that ?Kis a bounded domain, using Poincainequality, then According to (3.51)-(3.54), we infer From (3.45)-(3.48), (3.55), for all t ≥τ, g ∈, ut∈Ug(t+τ,τ)B, we get that Step 2: We consider the functional differential system (3.42). By (1.2), we get and For δ >0 small, it follows from (3.56)-(3.58) that Applying the Gronwall Lemma in the intervalwe infer Noting that ?Kis a bounded domain,using Poincinequality,and by Lemma 3.2 and Lemma 3.3, we can choose t and m large enough such that and Combining with (3.60)?(3.63), for0 andwhen we choose t and m large enough such that This complete the proof. For Equ.(3.44), similar to the proof of Lemma 3.4, we get the following conclusion. Lemma 3.6 Under the assumptions of Lemma 3.2, for any fixed, anyand every bounded set B ?CV, there exist K >0 and T >0 such that ?t ≥T, g ∈H(g0), φ ∈B,∈Ug(t,τ)φ, and={x ∈RN Now, we state our main results. Theorem 3.7 (Existence of Uniform Attractor)Under the assumptions Lemma 3.2,then the family of multi-valued processespossesses an unique uniform attractorin Proof By Lemma 3.2, we know that the multi-valued processes {Uσ(t,τ)}σ∈Σis uniformly dissipative,and according to Lemma 3.5,Lemma 3.6 and Theorem 2.4,the multi-valued processes {Uσ(t,τ)}σ∈Σis uniformly ω-limit compact. Then, by Theorem 2.3, the family of multi-valued processes{Uσ(t,τ)}σ∈Σpossess an unique uniform attractorin CH1(RN).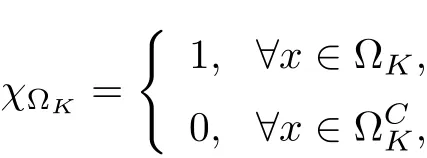
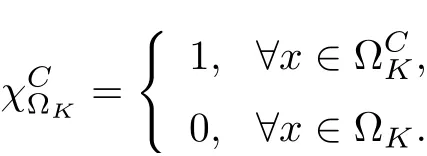
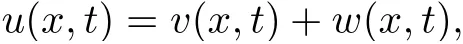
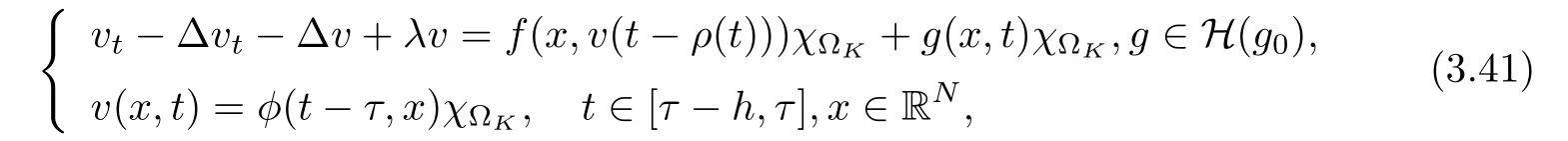
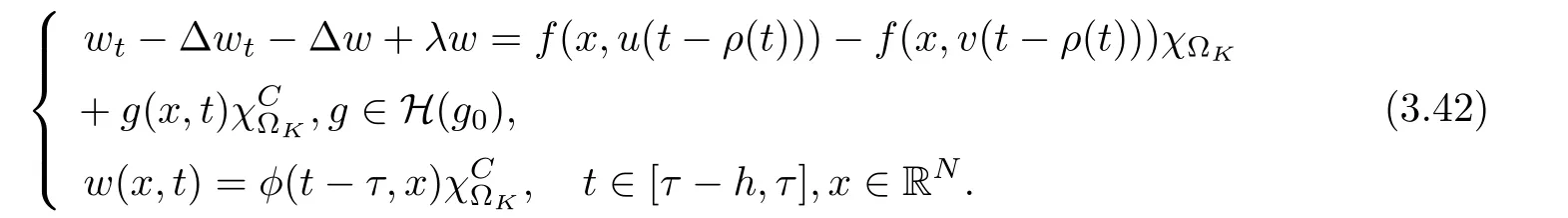

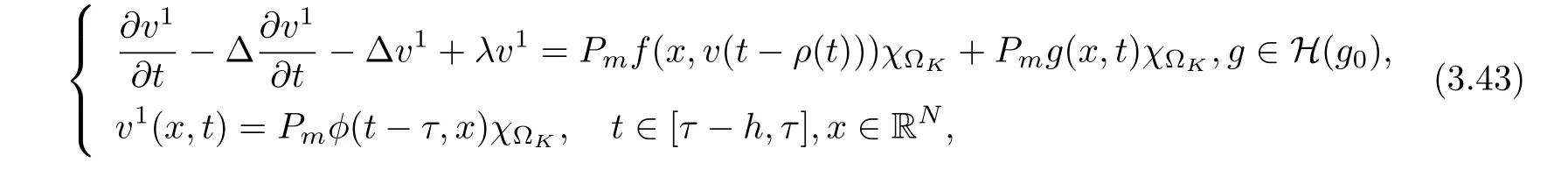
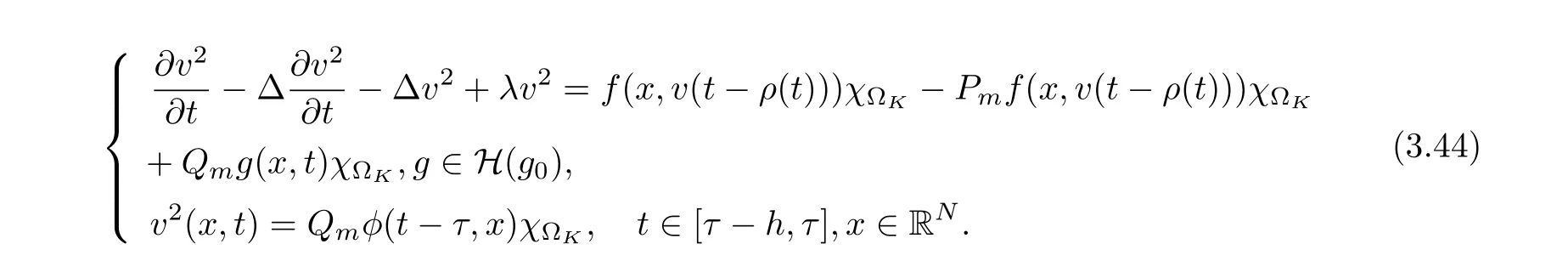
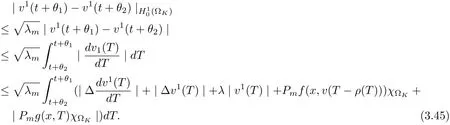
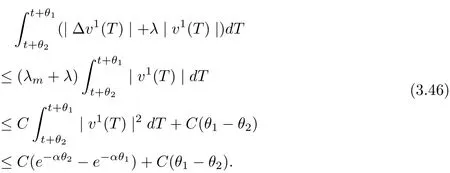
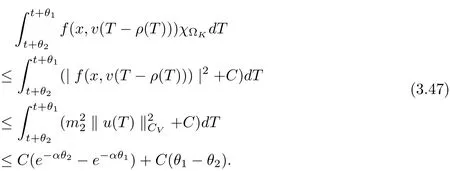
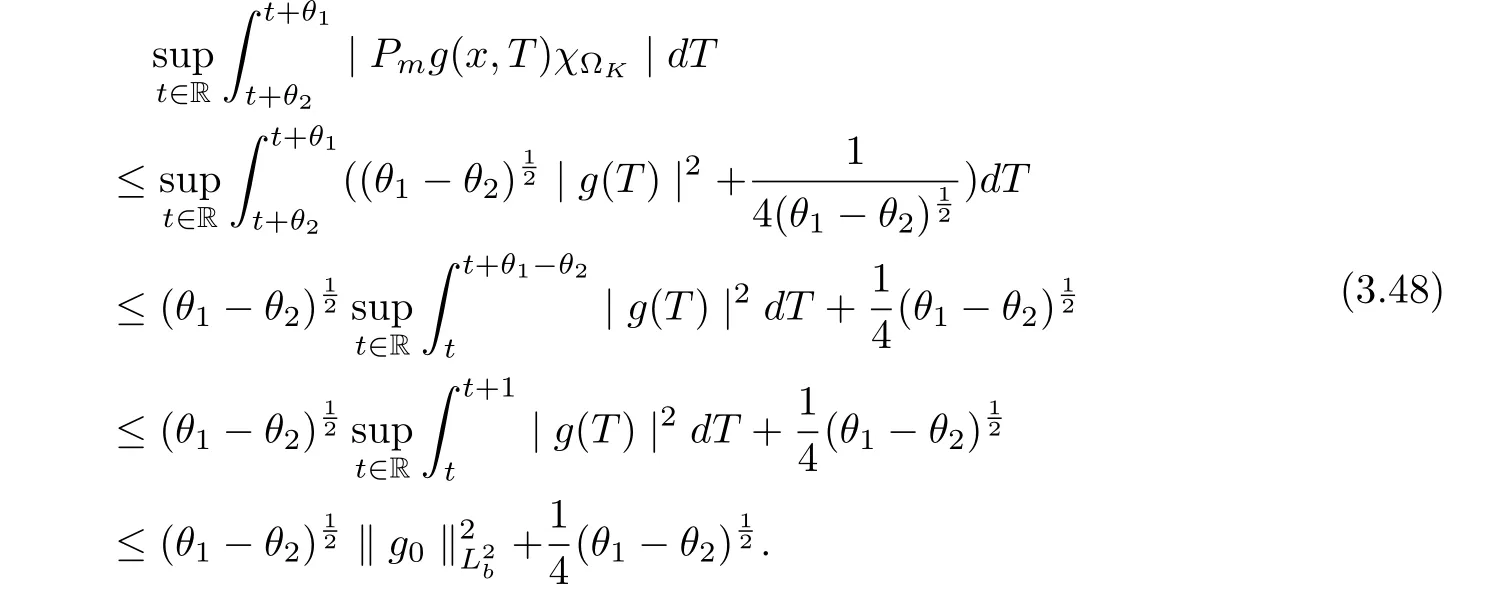
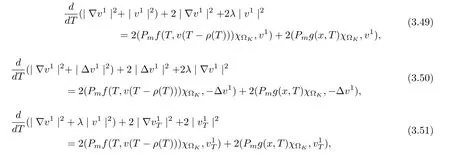
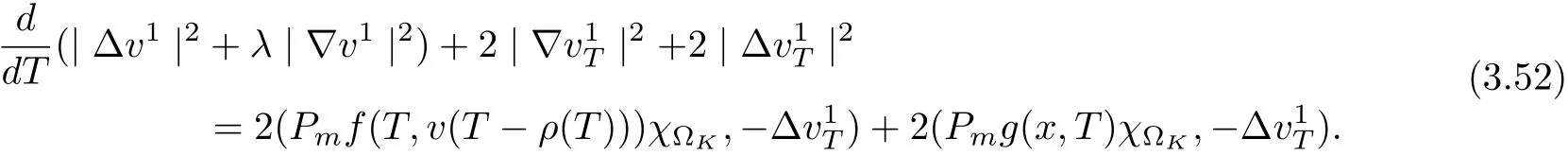
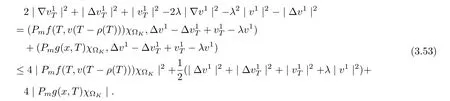
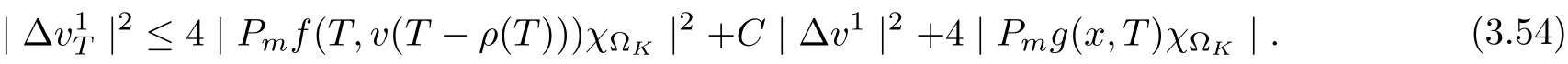
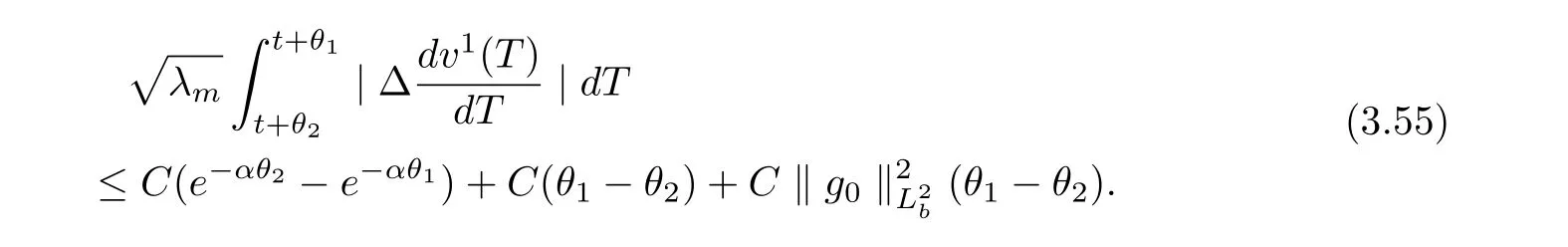
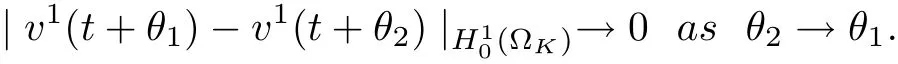
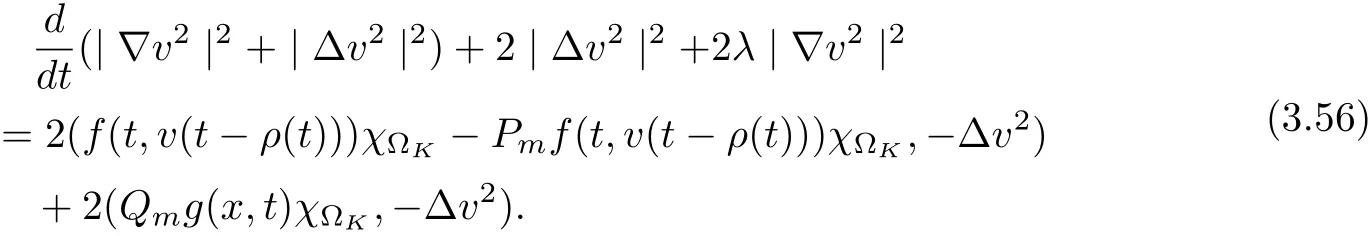
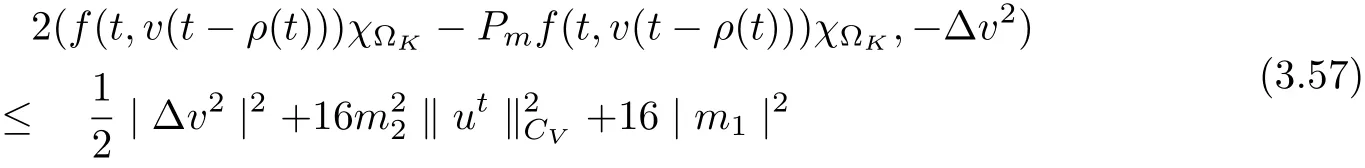
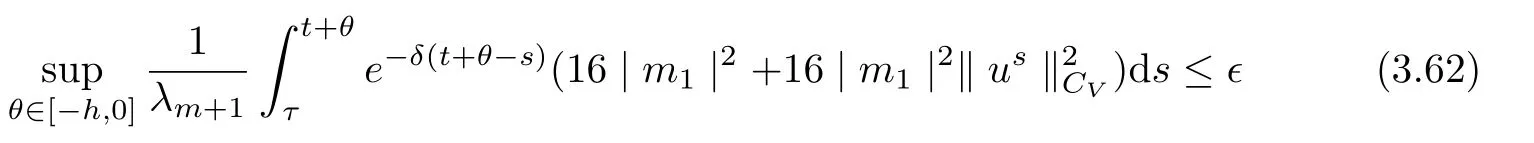
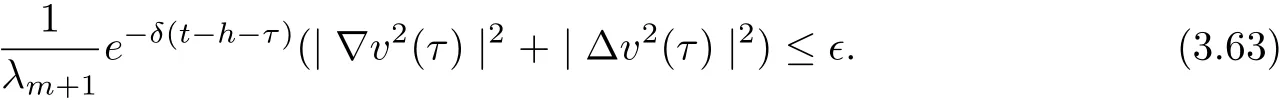
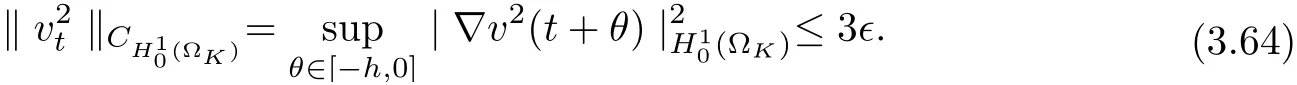
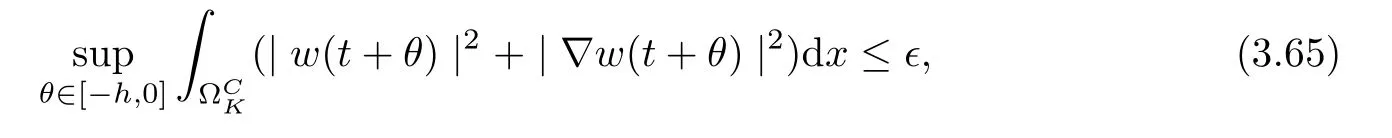
 Chinese Quarterly Journal of Mathematics2019年4期
Chinese Quarterly Journal of Mathematics2019年4期
- Chinese Quarterly Journal of Mathematics的其它文章
- Research on Robust Cooperative Dual Equilibrium with Ellipsoidal Asymmetric Strategy Uncertainty
- Global Stability of An Eco-epidemiological Model with Beddington-DeAngelis Functional Response and Delay
- Existence and Multiplicity of Periodic solutions for the Non-autonomous Second-order Hamiltonian Systems
- Some Random Coincidence Point and Common Fixed Point Results in Cone Metric Spaces Over Banach Algebras
- Global Existence of Solutions to The Keller-Segel System with Initial Data of Large Mass
- On Products and Diagonals of Mappings in Generalized Topological Spaces
