Descent Equations Starting from High Rank Chern-Simons?

Bei Kang(康貝),Yi Pan(潘一), Ke Wu(吳可),Jie Yang(楊潔),and Zi-Feng Yang(楊紫峰)

1School of Mathematical Sciences,Capital Normal University,Beijing 100048,China

2School of Mathematics and Statistics,Henan University,Kaifeng 475004,China

1 Introduction

In the early 1970s,Wess and Zumino introduced effective Lagrangian in four-dimensional quantum field theory with supersymmetry,which is called Wess-Zumino term(WZ term)nowadays.[1]After that,Witten tried to gauge the WZ term by trial and error and obtained gauged WZ term in 1983[2]called Wess-Zumino-Witten term(WZW term)subsequently.Chou,Guo,Wu,and Song[3]got the complete WZW term by means of geometric and topological consideration.From then on,the geometric properties of WZW term have been widely discussed and studied.[4]Among these works,Chern-Simons forms are the signi ficant part in the study of WZW term.Chern-Simons forms were named after Chern and Simons for their work.[5]They are also important in gauge theory.Since then,the WZW term and the anomaly become significant in the researches of quantum gauge theory and mathematical physics.Many works of anomalies in quantum gauge theory came out in the view point of geometric and topological methods,[4,6]which are the topological origin of quantum anomaly.Since a physical theory should be anomaly free,many physicists devote to looking for anomaly cancellation.Among them,Green and Schwarz discovered Green-Schwarz mechanism.[7]Their work also solved the big anomaly problem in superstring theory.Hence it inspired the first revolution of superstring theory.In the study of the anomaly,many works have been focused on descent equations.[4,8]They appeared to be very important in understanding the essence of the anomaly.

Recall that the descent equations are also called zigzag equation,[9]

where k=1,...,r(will be explained in Subsec.2.1).The last term of these equations is

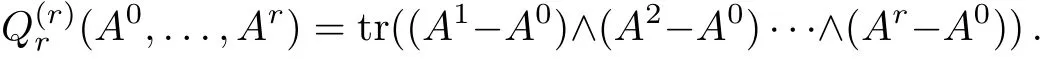
It is a differential r-form,where the descent equations terminate.

In the work of Ref.[10],Alekseev,Naef,Xu,and Zhu expanded descent equations in the case of r=2.They combined Kashiwara-Vergne theory with descent equation to establish a correspondence between solutions of Kashiwara’s first equation in the Lie theory and universal solutions of descent equations of r=2.The solutions of their expanded descent equations are given as follows,

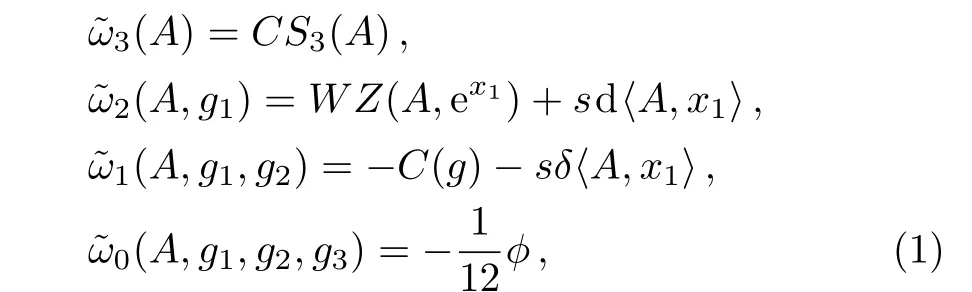
Our main work is to give a degree completion of general descent equations to obtain the general solutions.In other words,we can get all solutions from(2r?1)-form,(2r?2)-form,...,down to 1-form and 0-form.Among these differentials,1-form and 0-form are the key parts to construct.In the second section of this paper,we provide a detailed construction of our descent equations for r=2.Then in the third section,we use free Lie algebra to construct the space of differential forms.Furthermore in this new space,we give a new interpretation of 1-form and 0-form solutions of descent equations.In the last section,we derive general solutions of descent equations for r>2.

2 Chern-Simons Type Characteristic Classes and Descent Equations ofr=2

In the first part of this section,we review descent equations defined in Ref.[4]and an expansion of them for the case r=2 by Alekseev et al.[10]Then we describe new expanded descent equations of r=2 different from those in Ref.[10].The term ω3in our expanded descent equations coincides within Eq.(1)from Ref.[10].However,ωiis different fromfor i=0,1,2.The advantage of our formalism is that it can be generalized to more cases.We will explain the generalization of our descent equations for r>2 in Sec.4.

2.1 Descent Equations and Their Expansion at r=2

Let G be a connected Lie group with Lie algebra G,and E be a principle G bundle over a C∞-manifold M with projection π :E → M.Assume P is an invariant polynomial of degree r,that is,a symmetric,multilinear map fromto C invariant under the inner automorphism of G on Gr.If A∈?1(E,G)is a connection on E and F=dA+(1/2)[A,A]is the corresponding curvature,then we have

The above proposition is generalized in Ref.[6]by introducing the following concept of Chern-Simons type characteristic classes.

Given k+1 connections A0,A1,...,Akon the principal G bundle E,we define

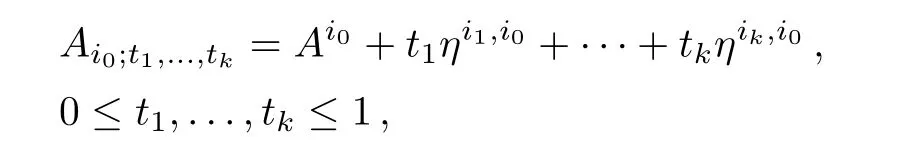
where ηi,j=Ai? Aj.The curvature of Ai0;t1,...,tkis

The Chern-Simons type characteristic classes,or the k-Chern-Simons Q-cochain,is defined as follows

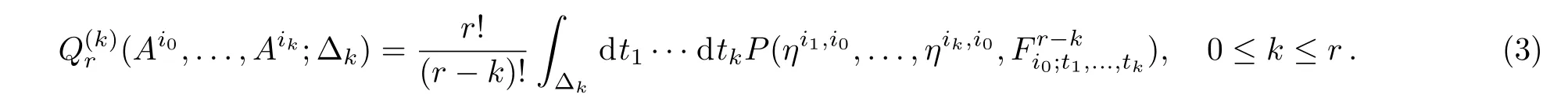
A marvellous property of k-Chern-Simons Q-cochain is given in the following theorem,which generalizes the formula(2):

Theorem 1[6]The following equation holds

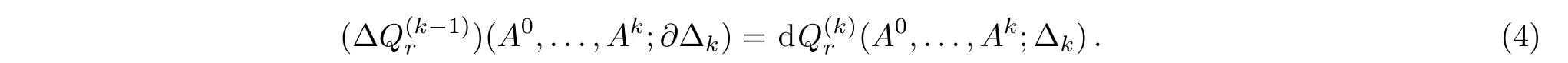
Here?is an operator acting on a polynomial R(k)(A0,...,Ak)by

where the symbol“?”over Aiindicates that Aiis deleted from the sequence A0,...,Ak+1.It is easy to see?2=0,thus? is a coboundary operator.According to Theorem 1,the coboundary of the(k?1)-Chern-Simons Q-cochain equals the exterior differential of a k-Chern-Simons Q-cochain.

Take r=2 as an example.For any g1∈G,take A0=0,A2=A,and A1=Ag1=Ag1+g1?1dg1representing a gauge transformation of A,descent equations(4)shall be

Recently Alekseev et al.gave descent equations ending with a 0-form in Ref.[10].As shown in that paper,a new operator δ is defined,and it induces the following descent equations

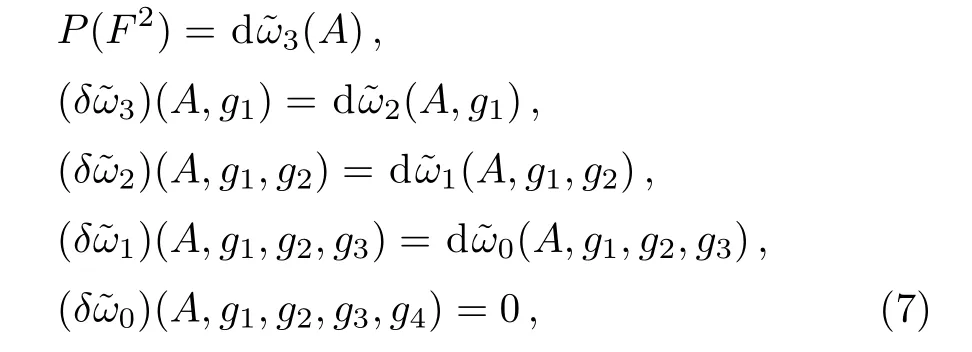
2.2 Another Solution of Descent Equations in r=2

Motivated by paper Ref.[10],we consider if there exist more general descent equations ending with a 0-form,that is,for any case of r=2,3,...We define an operator δ which acts on a polynomial R(A,g1,...,gk)consisting of A,g1,...,gk,dA,dg1,...,dgkwith the rule

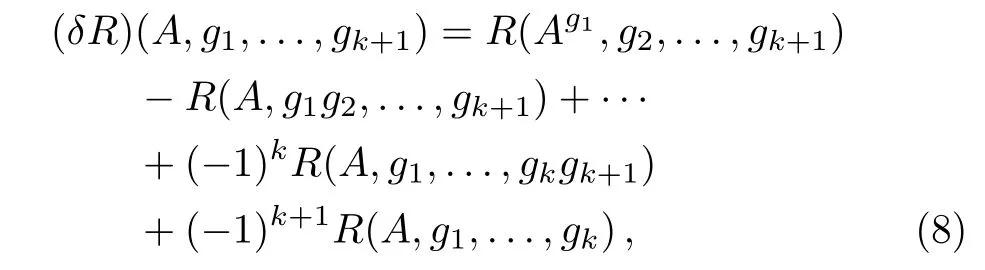
where g1,...,gk+1are elements of G. Note that the operator δ defined above acts on polynomials of A,g1,...,gk,dA,dg1,...,dgk. In fact,it acts on the space of differential forms D?x1,...,xn?defined in Subsec.3.1(see Subsec.3.1 for details).Hence the operator δ defined by Eq.(8)is different from the one defined in Ref.[10],which acts on forms in WG??(Gk),where WG is the Weil algebra(see Ref.[10]).It is easy to check that δ2=0 and we have the following descent equations,

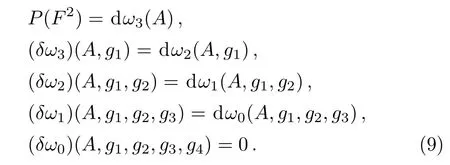
Here ω3(A)=CS3(A)=(0,A).Equations(9)look like(7),but the respective spaces in which they live are totally different.We would like to write down the expressions of ωi’s(i=0,1,2)in the new space.According to the definition of δ,we can compute the following equations

As a consequence,

which means ω2(A,g1)and×(Ag1,A)differ by a cocycle.Here we depict the primitivity of(Ag1,A)in terms of hP,the Poincare homotopy operator(See Ref.[11]for more details).Thus we can choose ω2(A,g1)to be((0,Ag1,A)?(Ag1,A)),other than WZ(A,ex1)+s?A,x1?in Ref.[10].As one can see,g1in ω2(A,g1)represents the gauge transformationof A.We continue our computation of ω2(A,g1,g2),

Notice that the first term in the last line in Eq.(10)is a closed form.In fact,

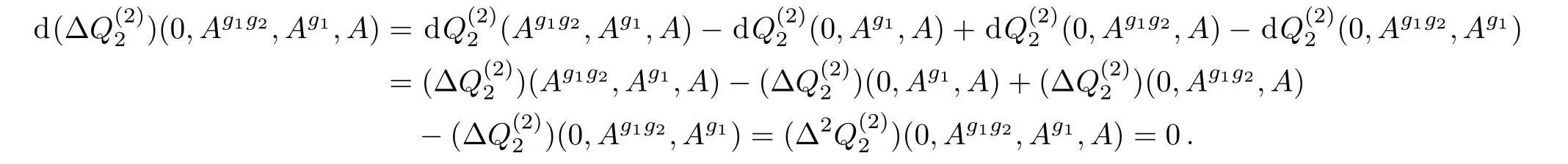
Hence it is acceptable to write ω1(A,g1,g2)formally as

for a certain u ∈ tDer2.The construction of ω1depending on d(div(u))will be explained in the next section in details.It can be verified that the construction satis fies the whole computation.Note that ω1(A,g1,g2)is different from(A,g1,g2)in Ref.[10]too.So far we obtain expressions for ω2(A,g1)and ω1(A,g1,g2),the remaining task is only to find ω0(A,g1,g2,g3).We would like to continue clarifying the conditions that ω0(A,g1,g2,g3)should satisfy

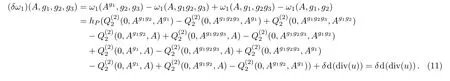
From the computation Eq.(11)we know ω0(A,g1,g2,g3)shall satisfy

So far we have deduced our descent equations for r=2,but we have not written down the expression for ω0.We will give an expression of ω0(A,g1,g2,g3)as well as an explanation of d(div(u))in the next section.The procedure will be stated in the language of free Lie algebra,mainly based on Ref.[12].

3 Construction ofω0

This section begins with some basic concepts in free Lie algebra,and then proceeds to constructing a new space of differential forms D?x1,...,xn?which contains ωi’s in Eq.(9),especially ω1and ω0.Next,a cosimplicial complex is brought in to provide a description of our descent equations(9).Finally,we shall focus on a Lie subalgebra tDernof Dern,the Lie algebra of derivations of Lien.In this part,we give a new definition of differential operator d acting on tDern.

3.1 The Space of Differential Forms and Cosimplicial Complex

Let F be a field of Char(F)=0.Over F,we define Lien=Lie(x1,...,xn)to be the degree completion of the free Lie algebra generated by n letters x1,...,xn.For the sake of further discussions,Lienis equipped with a gradation Lien=Liei(x1,...,xn),where elements in Liei(x1,...,xn)are constituted by i letters.

Let Assn=U(Lien)be the universal enveloping algebra of Lien,so it is the degree completion of the free associative algebra generated by x1,x2,...,xn.Therefore,each element b∈Assncan be written uniquely asDefine the linear operators?i(i=1,...,n)on b by?ib=bi.Then b has a unique decomposition

Example 1For b=x1?x2+x2?x3+x3?x1,we know?1b=x3,?2b=x1,?3b=x2according to the definition,we easily get b=(?1b)? x1+(?2b)? x2+(?3b)? x3.

Define the graded vector space trn=/span{a?b?b?a},?n,a,b∈,whereconsists of elements possessing a positive degree in Assn.It should be noticed that trndoes not inherit the product operation of Assn.

With all the above preparations,we shall constructthespacetowhich ωi’sbelong. Consider Lie(x1,...,xn,dx1,...,dxn),a free graded Lie superalgebra with generators x1,...,xn,dx1,...,dxn. Here we assume deg(xi)= 0,deg(dxi)= 1 as usual.Then a monomial in Lie(x1,...,xn,dx1,...,dxn)has two degrees: one is the sum of degrees of generators,and the other is the number of letters constituting it. As described earlier,the universal enveloping algebra of Lie(x1,...,xn,dx1,...,dxn) is Ass(x1,...,xn,dx1,...,dxn)= U(Lie(x1,...,xn,dx1,...,dxn)). Define the space of differential forms as D?x1,...,xn?=Ass+(x1,...,xn,dx1,...,dxn)/span{a?b ? (?1)dega·degbb ? a},a,b ∈ Ass+(x1,...,xn,dx1,...,dxn),where elements in Ass+are constituted at least by one letter.Here we construct a new space of differential forms D?x1,...,xn?rather than the one in Ref.[10]since the latter is not suitable for descent equations of general r.In fact,it is difficult to find solutions belonging to the space of differential forms defined in that paper for descent equations for any r≠2.

Example 2Let A be a generator satisfying deg(A)=1.The space of differential forms defined by A is D?A?=Ass+(A,dA)/span{a ? b? (?1)dega·degbb? a}, ?a,b ∈Ass+(A,dA).Denote A as a generator satisfying deg(A)= 1,and x1,...,xnas generators satisfying deg(xi)=0,i=1,...,n.We shall have a cosimplicial complex defined as

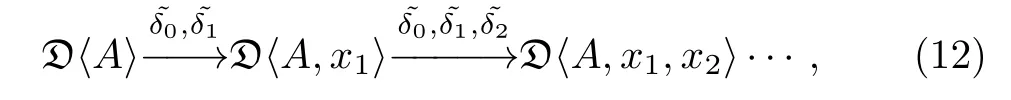
Theorem 2The differential?δ coincides with the operator δ defined in Eq.(8).

ProofWe only need to define the map φ :exi7→ gi.?

3.2 Tangential Derivation Space

Similar to the inner derivation of Lie algebra,the tangential derivation is defined as a derivation u such that u(xi)=[xi,ai]for i=1,...,n,where ai∈Lien.We denote u as(a1,...,an)for convenience of calculations in the context.

Proposition 1The space of tangential derivations tDerncarries a Lie algebra structure,which suggests that tDernis a Lie subalgebra of Dern.(See Ref.[12]for a proof.)

The action of the permutation group Snon tDernis induced by its action on Lien.For σ∈Sn,it follows that

Define a simplicial map from tDernto tDern+1such that the image of u=(a1(x1,...,xn),...,an(x1,...,xn))is u1,2,...,n=(a1(x1,...,xn),...,an(x1,...,xn),0).By composing it with the permutation group Sn+1,we can get other maps,which are called simplicial maps too.

There is another family of simplicial maps[13]from tDernto tDern+1,sending u=(a1(x1,...,xn),...,an(x1,...,xn))to

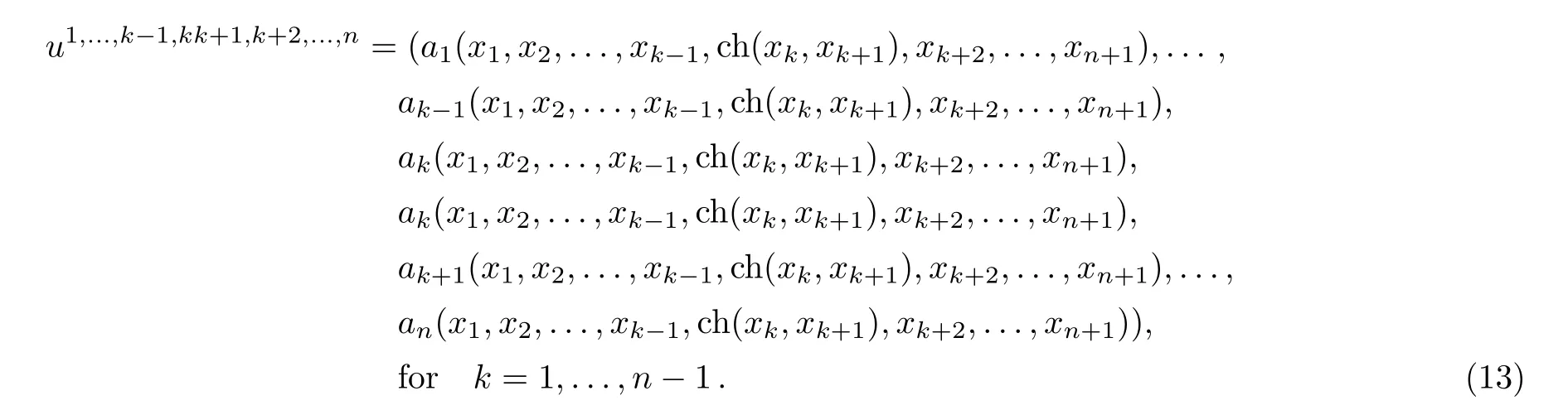
RemarkAll simplicial maps defined above are Lie algebra homomorphisms.

Example 3For u=(a1(x1,x2),a2(x1,x2)),we have u1,2=(a1(x1,x2),a2(x1,x2),0).Thus

Apart from simplicial maps,we define a differential d from tDernto tDern+1given by

Note that the differential d that we defined above is different from the one defined in Ref.[12],since u12,3,...,n+1,...,u1,2,...,nn+1in Eq.(14)have different meanings from the ones in Ref.[12].It can be checked that d2=0.Since ω1(A,g1,g2)∈ D1?A,x1,x2?,it requires a bridge between tDernand D??A,x·?.Hence we introduce a map

Example 4Assume u=(a1(x1,...,xn),...,an(x1,...,xn))is a tangential derivation.Then

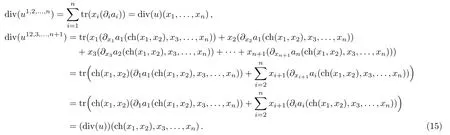
Proposition 2div(du)=

Proof

As stated in the previous section,

Thus we can take ω0(A,g1,g2,g3)to be div(du),since δdiv(du)= δ2div(u)=0.This completes descent equations(9).

4 General Descent Equations

We would like to point out that our construction works for more general cases.For the case of r=3,for example,the descent equations induced by δ shall be

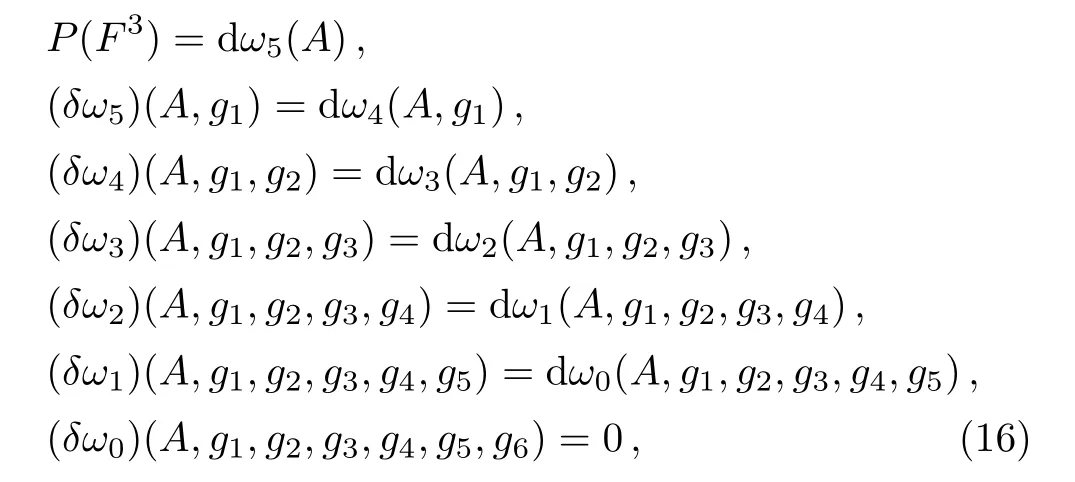
where

Here u∈tDer4,α(A,g1,g2,g3)∈D1?A,x1,x2,x3?can be any 1-form consisting of A and(i=1,2,3).We provide a computation below.Let us begin with ω4(A,g1),

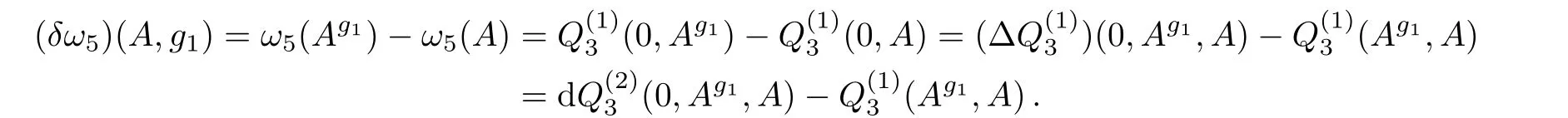
Similar to the discussion of ω2in the Subsec.2.2,

which shows that ω4(A,g1)differs fromby a cocycle.We choose ω4(A,g1)to beand continue our computation of ω3(A,g1,g2),

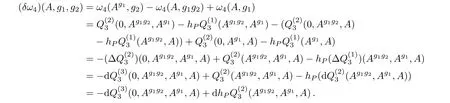
The latter term in the last line in Eq.(18)is a closed form.In fact,

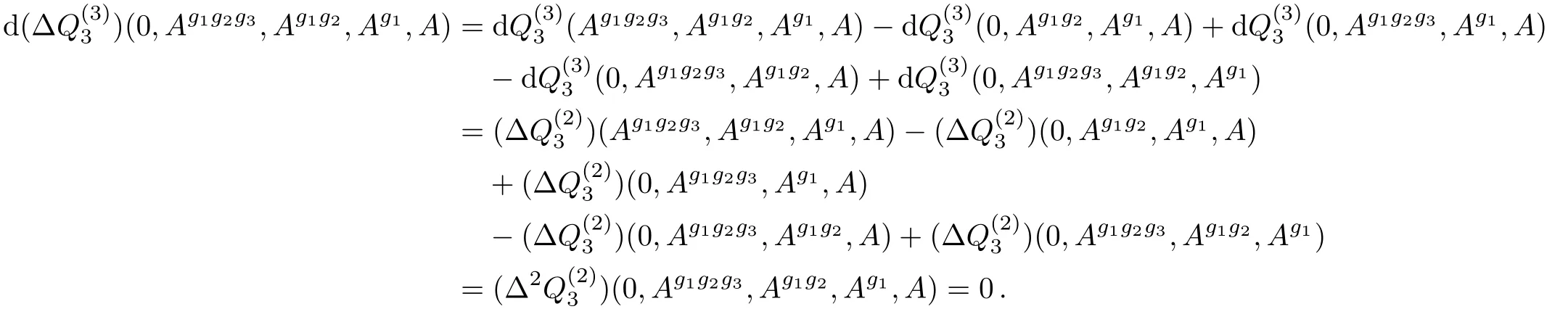
Hence we write ω2(A,g1,g2,g3)formally as

where α(A,g1,g2,g3) ∈ D?A,x1,x2,x3?.There is no doubt that we can continue in the following way

Since

and

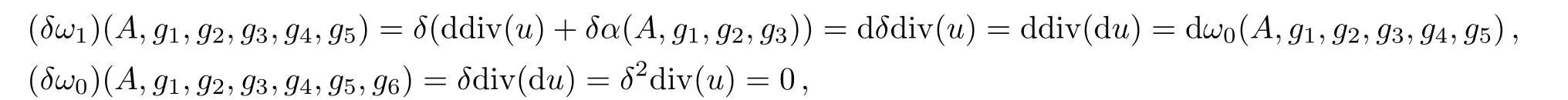
Eqs.(17)are exactly solutions of descent equations(16).

In a similar way,we can construct descent equations for other general cases.We shall write down these equations and their solutions without detailed computations as follows,

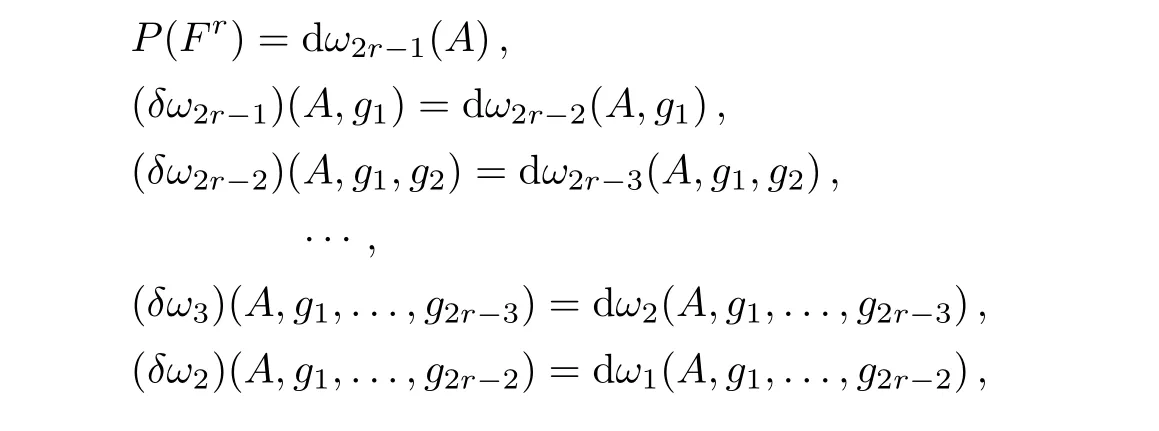
where

Here θk=1 if(2r?k) ≡ 1(mod 4)or(2r?k) ≡ 2(mod 4),otherwise θk= ?1,for k=r?1,r,...,2r?2.αr?1(A,g1,...,gr)can be any forms in Dr?1?A,x1,...,xr?,so are αr?2(A,g1,...,gr+1)in Dr?2?A,x1,...,xr+1?,...,α2(A,g1,...,g2r?3)in D2?A,x1,...,x2r?3?.u ∈ tDer2r?2.

Acknowledgement

We are grateful to S.K.Wang for helpful discussions.

[1]J.Wess and B.Zumino,Phys.Lett.B 37(1971)95.

[2]E.Witten,Nucl.Phys.B 223(1983)422.

[3]K.C.Chou,H.Y.Guo,K.Wu,and X.C.Song,Phys.Lett.134B(1984)67.

[4]B.Zumino,Y.S.Wu,and A.Zee,Nucl.Phys.B 239(1984)477;H.Y.Guo,B.Y.Hou,S.K.Wang,and K.Wu,Commun.Theor.Phys.4(1985)145;K.C.Chou,H.Y.Guo,K.Wu,and X.C.Song,High Ener.Nucl.Phys.(In Chinese)8(1984)252;K.C.Chou,H.Y.Guo,K.Wu,and X.C.Song,Commun.Theor.Phys.3(1984)593;K.C.Chou,H.Y.Guo,K.Wu,and X.C.Song,Commun.Theor.Phys.3(1984)73;K.C.Chou,H.Y.Guo,K.Wu,and X.C.Song,Commun.Theor.Phys.3(1984)125;K.C.Chou,H.Y.Guo,X.Y.Li,et al.,Commun.Theor.Phys.3(1984)491;C.H.Chang,H.Y.Guo,and K.Wu,Commun.Theor.Phys.3(1984)707;K.C.Chou,H.Y.Guo,and K.Wu,Commun.Theor.Phys.4(1985)91;H.Y.Guo,B.Y.Hou,S.K.Wang,and K.Wu,Commun.Theor.Phys.4(1985)233;H.Y.Guo,S.K.Wang,and K.Wu,Commun.Theor.Phys.4(1985)509;H.Y.Guo,B.Y.Hou,S.K.Wang,and K.Wu,Acta Phys.Sin.(in Chinese)35(1986)89.

[5]S.S.Chern and J.Simons,Ann.Math.99(1974)48.

[6]H.Y.Guo,K.Wu,and S.K.Wang,Commun.Theor.Phys.4(1985)113.

[7]M.B.Green and J.H.Schwarz,Phys.Lett.B 149(1984)117.

[8]L.D.Faddeev,Phys.Lett.B 145(1984)81.

[9]H.Y.Guo,S.K.Wang,and K.Wu,Phys.Lett.167B(1986)396.

[10]A.Alekseev,F.Naef,X.M.Xu,and C.C.Zhu,arXiv:1702.08857

[11]L.Gallot,E.Pilon,and F.Thuillier,Mod.Phys.Lett.A 30(2015)1550102.

[12]A.Alekseev and C.Torossian,Ann.Math.175(2012)415.

[13]A.Alekseev and C.Torossian,C.R.Acad.Sci.Paris S′erie I 347(2009)1231.