Controlling Thermal Conduction by Graded Materials?

Qin Ji(季欽)and Ji-Ping Huang(黃吉平)

Department of Physics,State Key Laboratory of Surface Physics,and Key Laboratory of Micro and Nano Photonic Structures(MOE),Fudan University,Shanghai 200433,China

Collaborative Innovation Center of Advanced Microstructures,Nanjing 210093,China

1 Introduction

Thermal conductivity is the fundamental physical parameter that describes the ability of a material to conduct heat.How to design the distribution of thermal conductivities is particularly important for obtaining new kinds of thermal metamaterials[1?15](the concept of metamaterial has been widely adopted as a material structurally designed to have a new property or function other than naturally occurring materials or chemical compounds),like thermal cloaks,[1?2,5,7,9,16?17]thermal concentrators,[5,8]thermal transparency,[6]macroscopic thermal diodes,[10]and energy-free thermostat.[11]

However,according to the transformation theory of thermal conduction(which is based on the fact that the thermal conduction equation ful fills form invariance under coordinate transformations),[1]all the thermal cloaks[1?2,5,7,9]and thermal concentrators[5,8]are essentially graded materials whose thermal conductivities vary along the radius.Moreover,their effective thermal conductivities equal to those of the host medium outside the cloak or concentrator.As a result,the existence of cloaks or concentrators does not affect the distribution of temperature or heat flux in the host medium,thus yielding a kind of thermal invisibility.This encourages us to ask a more general problem:what is the effective thermal conductivity of graded materials with arbitrary gradation pro files?This has not been touched in the literature due to the lack of suitable methods.In this work,we manage to solve this problem,in order to control or manipulate heat transfer with a different degree of freedom.

2 Analytic Theory Based on a First-Principles Approach

We consider a graded circular material with radius r0subjected to a uniform density of heat flux J0along the x-axis,the temperature distribution of the system satisfies the thermal conduction equation depending on time t,?·J+ρc(?T/?t)=Q.Here,J,T and Q represent the density of heat flux,temperature,and heat energy generated per unit volume per unit time,respectively.ρ denotes the mass density of the object and c is the specific heat capacity.Using the Fourier law,J= ?κ(r)?T(where κ(r)is the thermal conductivity of the material,which is a function of the position r along the radius,r≤r0),for static cases without internal heat sources,the above thermal conduction equation reduces into

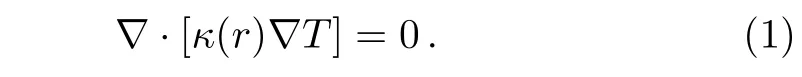
According to Eq.(1)in polar coordinates(r,θ),the temperature T satis fies

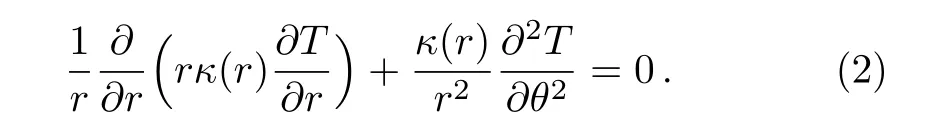
If we write T=R(r)Θ(θ)to achieve the separation of variables,we obtain

Without loss of generality,we set both r0and the thermal conductivity outside the material to be unit.If the thermal conductivity of the material has specific gradation pro files,the exact solution can be obtained by using the first-principles approach.For example,we give two examples in the following.

2.1 Exact Solution for Thermal Conductivity Distributed in a Power-Law Pro file

Assume that the thermal conductivity of the material increases outwards in a power-law form.In this case,κ(r)=arb(here a and b are two coefficients,b≥ 0;0≤r≤1),then Eq.(3)becomes

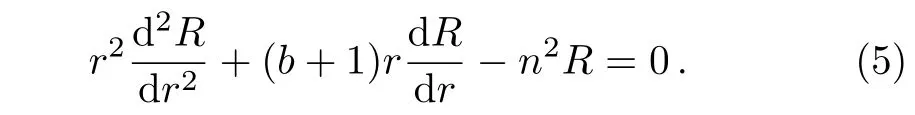
Since this equation is homogeneous,the solution has the form as R(r)=rs.Substituting it into Eq.(5)yields

In the far field where the host medium has a thermal conductivity of κm=1,the temperature is only determined bywhich means Tr→∞=?J0rcos(θ).In the material,the condition of convergence ensures that Tr→0= finite value.So the terms for s≥ 2 vanish.The temperature fields in the material and host medium are respectively given by

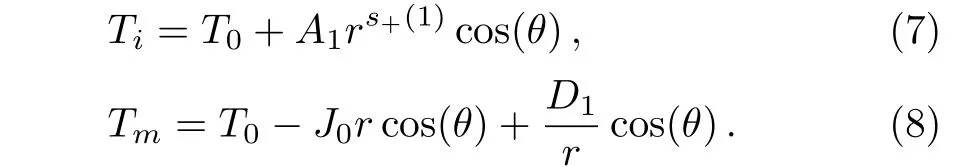
The coefficients are determined by the associated boundary conditions,

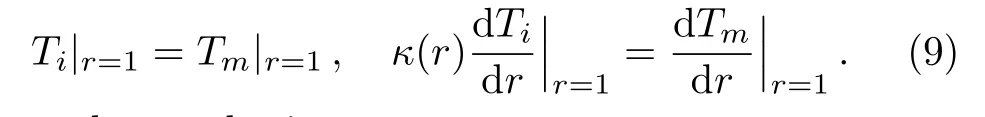
As a result,we obtain

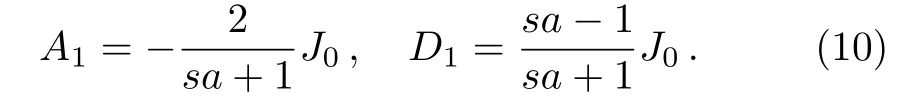
Since both the gradation pro file and the temperature boundary condition are symmetric,we concern more about the space variation of the temperature field along the x-axis,which can be written as

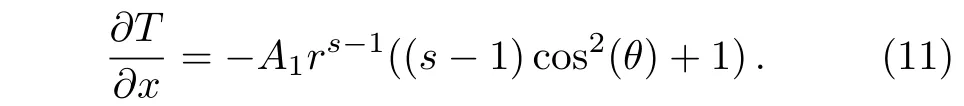
To analyze the response of the material to the external temperature field,we introduce the effective thermal conductivity κe.If the thermal conductivity distributed in the material is replaced by the uniform thermal conductivity κe,the value and gradient of the temperature at the boundary between the material and host medium will not change.In this case,the thermal medium with κeshows a dipolar effect on the external temperature field.So we obtain

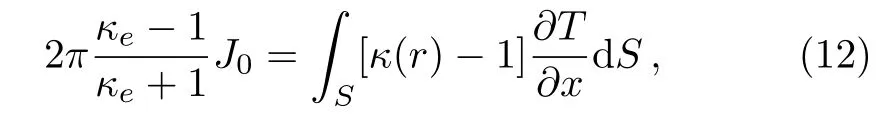
where S denotes the area occupied by the material.Calculating the above equation gives

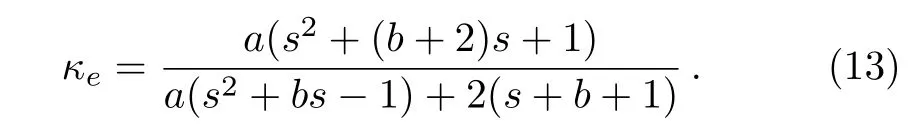
If b=0,κ(r)is a constant,and s=1.Then we achieve the desired result,

2.2 Exact Solution for Thermal Conductivity Distributed in a Linear Pro file

We consider a linear gradation pro file κ(r)=cr+d for the graded material,where c and d are two coefficients.The analytic procedure is much the same as in Subsec.2.1.For the sake of simplicity,we set?r=(d/c)r.Then,the radial function follows

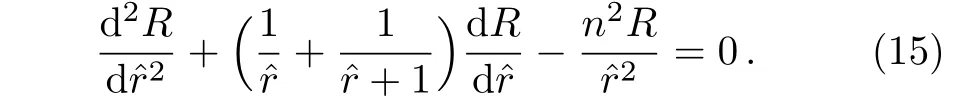
The power series solution can be expressed as

Substituting it into Eq.(15)yields

The coefficient of each term should vanish.After solving the lowest term,we can easily get

and the recursion relation

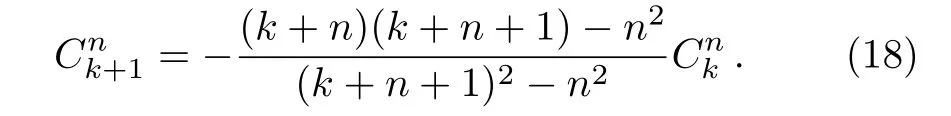
The series should be convergent for seeking the exact solution.Therefore,we require the condition of linear profiles with a small slope,which means|d/c|>1.Whereafter,the temperature fields in the material(Ti)and host medium(Tm)are respectively given by

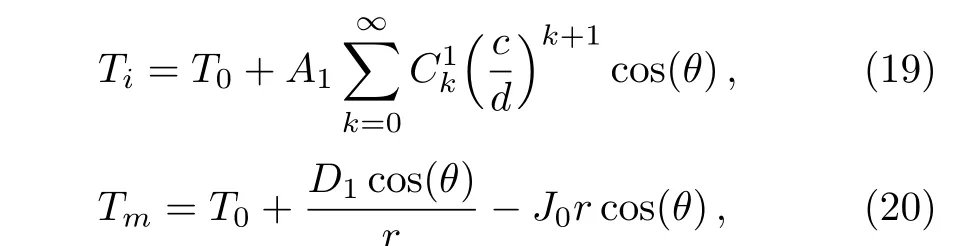
where

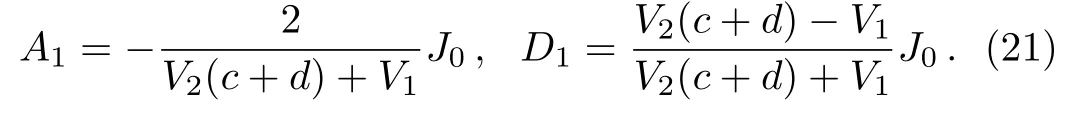
Here

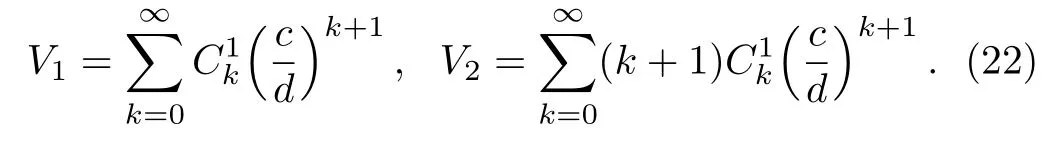
On the other hand,solving the temperature field along the x-axis yields

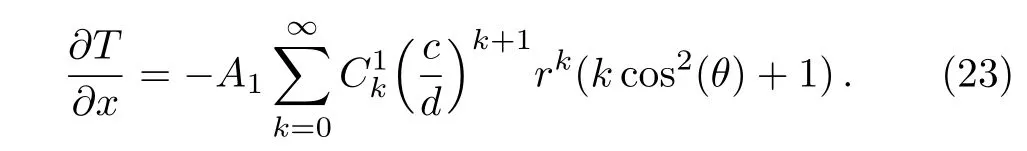
The substitution of Eq.(23)into Eq.(12)yields the effective thermal conductivity

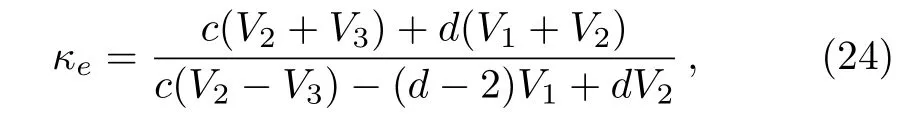
where

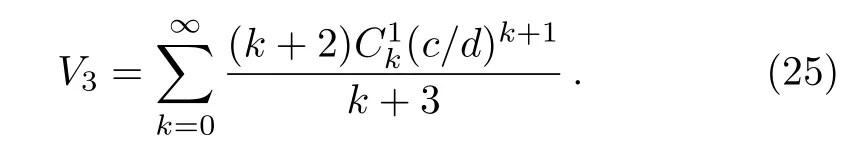
When c=0,κ(r)is a constant,and Eq.(24)reduces to the known case,

Now we are allowed to compare the exact solutions(Eq.(13)and Eq.(24))with the results obtained from the differential equation(Eq.(30)),in order to validate the above DAM.The numerical integration has been done by the fourth-order Runge-Kutta algorithm.Figure 1 shows power-law and linear gradation pro files of κ(r)with various coefficients.Clearly the DAM(Eq.(30))agrees with the exact results predicted from Eq.(13)(Fig.1(a))and Eq.(24)(Fig.1(b)),as expected.It is worth noting that the linear solutions should satisfy the small slope condition,which causes the lack of solutions when d is relatively small;see Fig.1(b).

Fig.1 (Color online)Effective thermal conductivity κefor two gradation pro files:(a) κ(r)=arband(b)κ(r)=cr+d.(a)κeversus a for different b;(b)κeversus d for different c.The solid lines denote the results calculated from the DAM(Eq.(30));the symbols are exact results predicted from(a)Eq.(13)and(b)Eq.(24).

3 Differential Approximation Method(DAM):A Differential Equation Approach

A graded material may be regarded differentially as a multi-layer structure.Let us start by considering a simple material that is composed of a homogeneous circular core(with thermal conductivity κc)plus a homogeneous circular shell(with κs).Solving Laplace’s equation and the associated boundary conditions yields the following expression for its effective thermal conductivity κe,

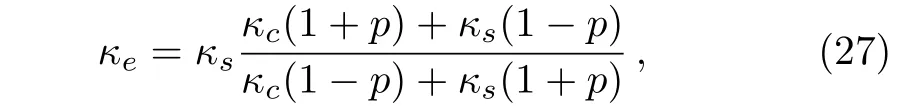
where p is the area fraction of the core.For the sake of convenience,we rewrite Eq.(27)as

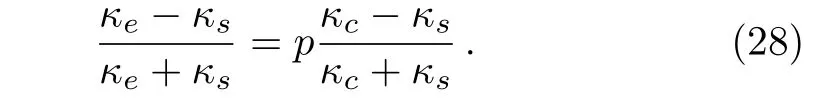
On the other hand,we construct a graded material with radius r.Then,we encircle the material with a shell of infinitesimal thickness dr.The effective thermal conductivity changes from κe(r)to κe(r+dr).In this case,Eq.(28)helps to obtain

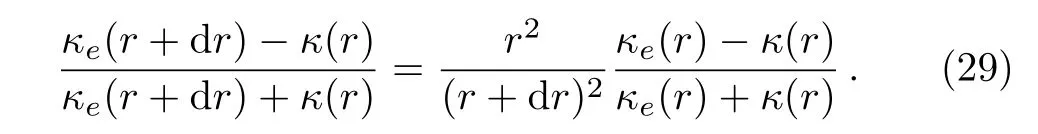
Here κ(r)is the thermal conductivity of the shell.Then,we obtain a differential equation,

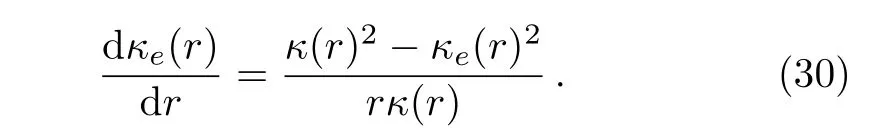
Given the gradation pro file κ(r)and the initial condition when radius is close to zero,the effective thermal conductivity of the whole graded circular material,κe(r),can be achieved according to Eq.(30).This differential equation requires that the thermal conductivity of each shell cannot be zero,of which the first-order derivative should be continuous.

Incidentally,the differential equation for the effective thermal conductivity of a graded spherical material can be readily obtained on the same footing,

4 Computer Simulations Based on a Finite-Element Method

By using COMSOL(https://www.comsol.com),we perform two-dimensional finite-element simulations to further con firm the validity of DAM.In the mean time,more detailed thermal responses of graded materials can be revealed.The basic parameters of our simulation system are set as follows.A graded circular material with the radius of 6 cm is embedded in the center of a square host medium with the side length of 20 cm.To maintain a uniform density of heat flux,the left side of the host medium holds a line hot source with temperature 313 K,while the right side 273 K.

Figures 2(a),2(d),2(g)show the simulation results for three different power-law gradation pro files. Figurs 2(b),2(e),2(h)represent effective thermal materials of Figs.2(a),2(d),2(g)respectively,whose thermal conductivities are computed according to both Eq.(30)and Eq.(13)(the two equations give the same results).The thermal conductivity of the host medium in Fig.2(a),2(b),2(d),2(e),2(g),2(h)has the same value,which equals the effective thermal conductivity of the graded material shown in Fig.2(d).Accordingly,we observe the different temperature patterns within the host medium areas in Figs.2(a),2(d),2(g)or Figs.2(b),2(e),2(h).For more detailed comparison,Figs.2(c),2(f),2(i)display the calculated difference between Fig.2(a)and Fig.2(b),Fig.2(d)and Fig.2(e),and Fig.2(g)and Fig.2(h),respectively.Clearly,Figs.2(c),2(f),2(i)show the zero value outside the circular material region,which further con firms the validity of(and agreement between)Eq.(30)and Eq.(13).

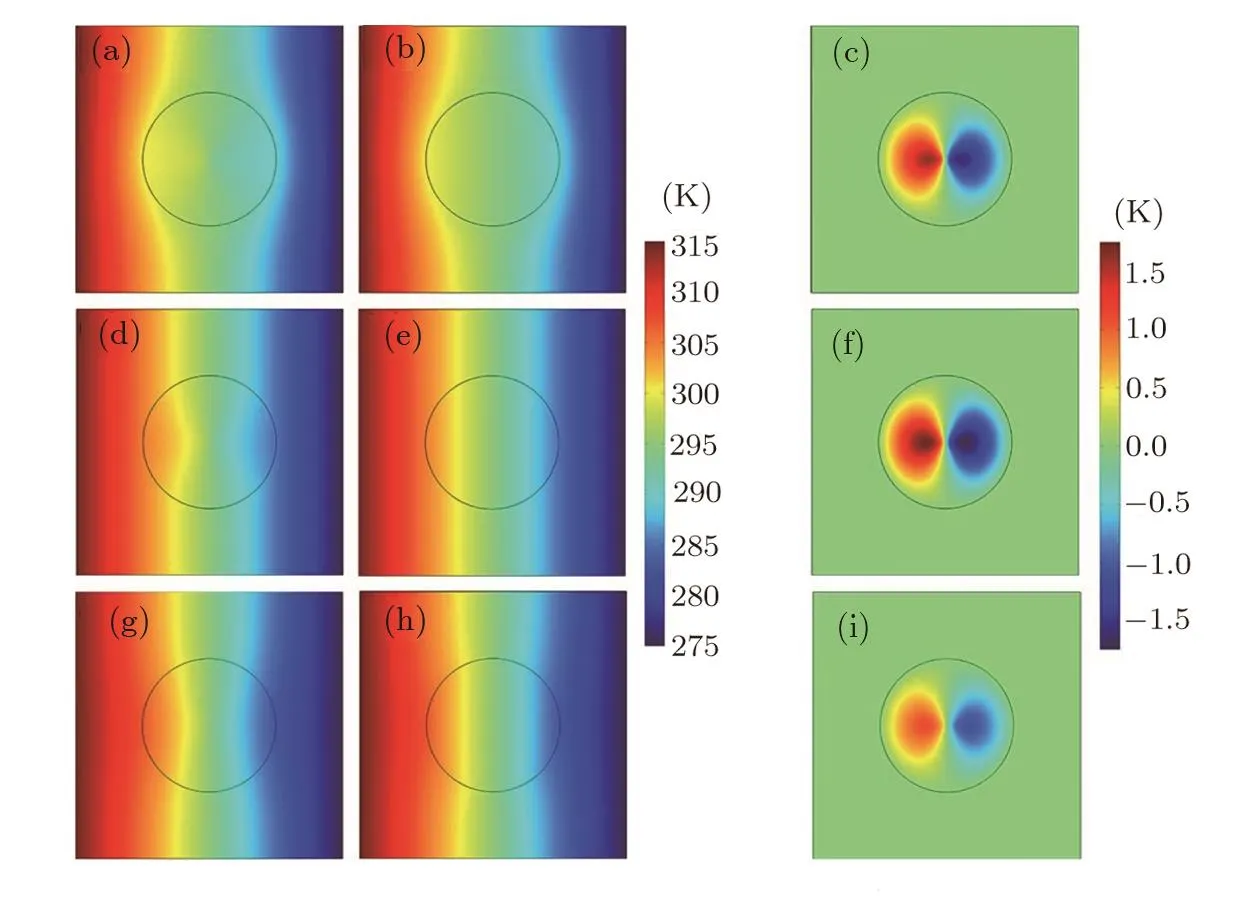
Fig.2 (Color online)Finite-element simulations for power-law gradation pro files.The color surfaces denote the distribution patterns of(a),(b),(d),(e),(g),(h)temperature and(c),(f),(i)temperature difference,as represented by the associated color bar.The thermal conductivity of the materials is(a)1.0r2,(b)10.36 W·m?1·K?1,(d)1.0r1,(e)3.09 W·m?1·K?1,(g)0.5r1,and(h)1.74 W·m?1·K?1;in(a),(b),(d),(e),(g),(h),the host medium has a thermal conductivity of 3.09 W·m?1·K?1.(c),(f),and(i)show the temperature difference between(a)and(b),(d)and(e),and(g)and(h),respectively.

The layout of Fig.3 is roughly the same as Fig.2,but for the graded material with linear gradation pro files in Figs.3(a),3(d),3(g).The thermal conductivities of materials in Figs.3(b),3(e),3(h)are different,which respectively equal to the effective thermal conductivity of Figs.3(a),3(d),3(g)according to Eq.(30)or Eq.(13).Similarly,Fig.3(c),3(f),3(i)display the zero value outside the circle area,which also helps to validate Eq.(30)and Eq.(13).

So far,both Figs.2 and 3 have shown that the DAM(Eq.(30))works well under the conditions of power-law or linear gradation pro files of thermal conductivity.Actually,the DAM is applicable for arbitrary gradation profiles,including multi-layer structures.See Fig.4.Figure 4 has the same layout as Fig.3,but displaying three multi-layer structures in Figs.4(a),4(d),4(g).The thermal conductivities adopted for the circular materials in Figs.4(b),4(e),4(h)are educed by the DAM(Eq.(30))for the multi-layer structures displayed in Fig.4(a),4(d),4(g)respectively.Note that by choosing the layer thicknesses appropriately,the effective thermal conductivities of the three multi-layer structures are exactly the same in Figs.4(a),4(d),4(g),as calculated by Eq.(30).Clearly,Figs.4(c),4(f),4(i)also display the zero value outside the multi-layer structure,which validates Eq.(30)for the multi-layer structure indeed.

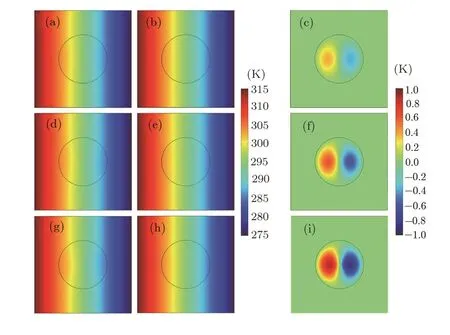
Fig.3 (Color online)Finite-element simulations for linear gradation pro files.The thermal conductivities of the host medium and the material are(a)5.64 W·m?1·K?1and 0.5r+4,(b)5.64 W·m?1·K?1and 5.64 W·m?1·K?1,(d)7.23 W·m?1·K?1and 1.0r+4,(e)7.23 W·m?1·K?1and 7.23 W·m?1·K?1,(g)10.39 W·m?1·K?1and 2.0r+4,and(h)10.39 W·m?1·K?1and 10.39 W·m?1·K?1.(c),(f)and(i)display the temperature difference between(a)and(b),(d)and(e),and(g)and(h),respectively.

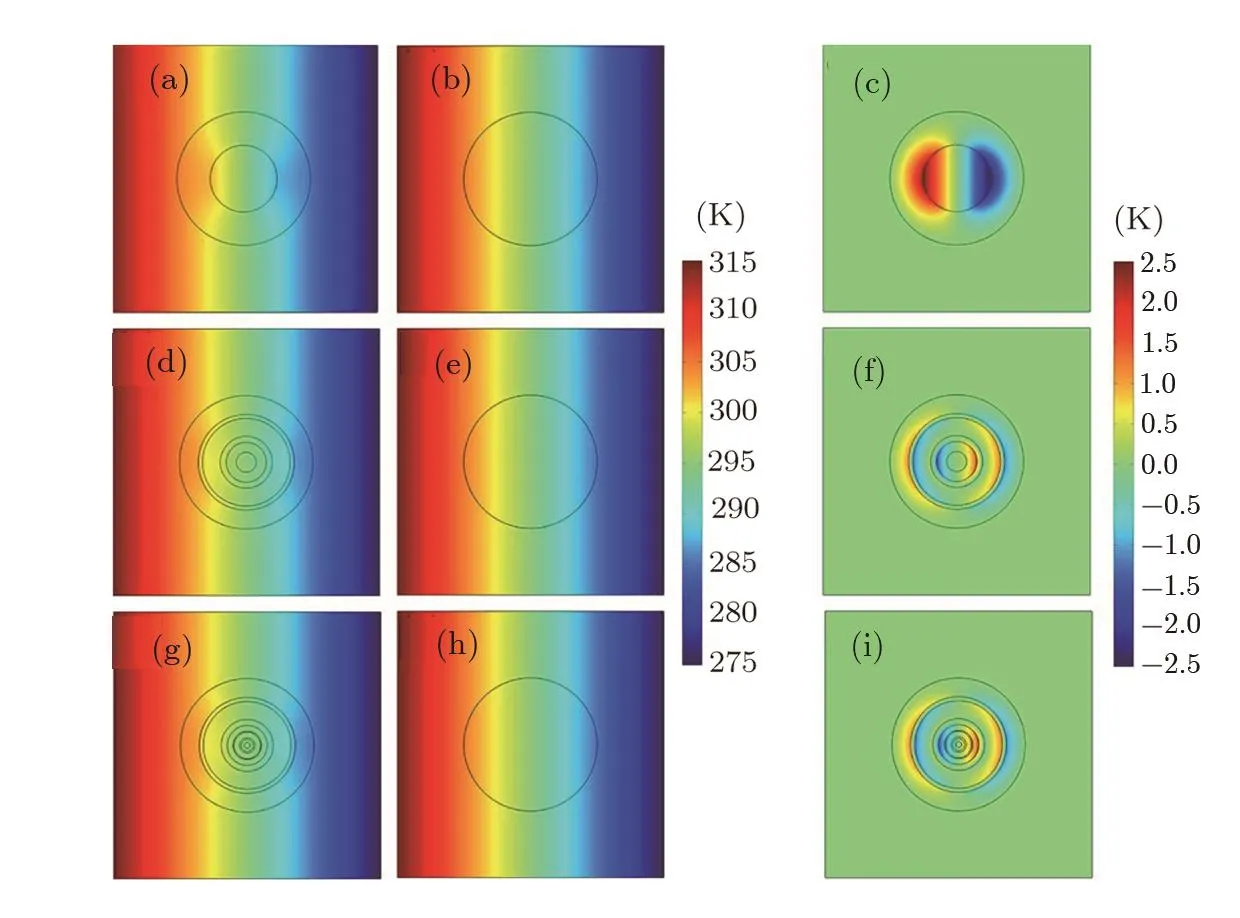
Fig.4 (Color online)Finite-element simulations for multi-layer pro files.In(a,d,g),the multi-layer material is made of two materials(with thermal conductivity 10 W·m?1·K?1and 90 W·m?1·K?1)in alternation:(a)two layers,(d)six layers,and(g)ten layers;the central layer of(a),(d),(g)has the thermal conductivity of 10 W·m?1·K?1.In(a),(b),(d),(e),(g),(h),the thermal conductivity of the host medium is 60 W·m?1·K?1.(c),(f)and(i)represent the temperature difference between(a)and(b),(d)and(e),and(g)and(h),respectively.

5 Experiments Based on a Multi-Layer Circular Structure

In order to further con firm the validity of the DAM(Eq.(30)),here we experimentally investigate a multilayer material. Our experimental design is shown in Figs.5(a),5(d).Figure 5(a)contains a six-layer material,which is made of two materials(copper and phosphor bronze)in alternation.For comparison,Fig.5(d)includes a homogeneous material(brass)with the thermal conductivity(109 W·m?1·K?1)equal to the effective thermal conductivity of the multi-layer material shown in Fig.5(a)calculated according to Eq.(30).The left-hand side of the host medium(copper)is connected with hot water,and the right-hand side immerged into cold water.A thermal imager is emplaced right above the multi-layer material.The experiment is conducted in the air.Air convection and thermal contact resistance are two possible factors affecting experimental accuracy,which,however,can be reduced by using appropriate approaches(e.g., fine welding).Figures 5(b),5(e)show the finite element simulations of Figs.5(a),5(d),respectively.Figures 5(c),5(f)exhibit the experimental results of Figs.5(a),5(d),respectively.Clearly the experimental results(Figs.5(c),5(f))echo with the simulation results(Figs.5(b),5(e)).Importantly,the temperature distribution patterns in Figs.5(b),5(c)are similar to those in Figs.5(e),5(f).This behavior indicates that our experimental results support the DAM(Eq.(30))indeed.

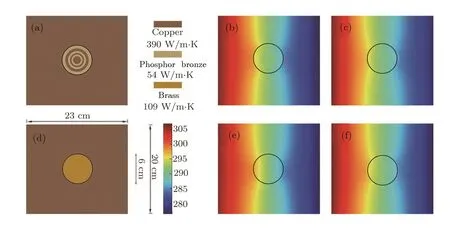
Fig.5 (Color online)Experimental results of a multi-layer material.(a)Experimental structure,(b) finite element simulation of(a),and(c)experimental measurement results of(a).(d),(e)and(f)are the reference group of(a),(b)and(c),respectively.The thickness of the experimental structures shown in(a),(d)is 0.03 cm;other parameters are indicated in the figure.

6 Discussion and Conclusions

We have derived both a first-principles approach and a DAM(differential approximation method;Eq.(30))for calculating the effective thermal conductivity of a circular material whose thermal conductivity varies along the radius with specific or arbitrary gradation pro files.This equation(Eq.(30))has been con firmed by analytic theory(based on a first-principles approach),computer simulations(based on a finite-element method),and experiments(based on a multi-layer circular structure).

Self-heating objects are common in nature,such as human bodies or electric equipments.Our DAM(Eq.(30))may hold for such self-heating cases under some conditions.For example,let us introduce a kind of self-heating multi-layer material and deduce the effective thermal conductivity.Here the self-heating means that the center of the multi-layer material is keeping at a constant temperature,which can be seen as another boundary condition in the thermal model.Meanwhile,the multi-layer material is located in a uniform density of heat flux along x-axis.What we aspire herein is that the thermal responses of the self-heating multi-layer material is just the same as a homogeneous material.On one hand,when there is no self-heating,we may resort to the DAM(Eq.(30)).The corresponding simulation results are shown in Figs.6(a),6(b),6(c).On the other hand,we need to make sure that the self-heating multi-layer material can be replaced by a homogeneous material.Considering the boundary conditions,we may derive the effective thermal conductivity κeat the view of the center of material as

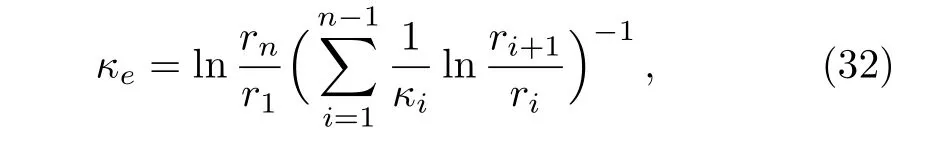
in which n is the total number of layers,and i is the serial number of each layer(with radius riand conductivity κi)of the multi-layer material from inside-out.Figures 6(d),6(e),6(f)show the simulation results.If the effective thermal conductivities calculated from the above two approaches(namely,Eq.(30)and Eq.(32))are coincidently identical,we can safely superpose the thermal effects induced by these two kinds of heat sources adopted in Figs.6(a),6(d).As a result,Fig.6(g)depicts a selfheating multi-layer material subjected to a uniform density of heat flux,which behaves just like a homogeneous material as shown in Figs.6(h)and 6(i).

This work is useful for designing new thermal metamaterials(including or going beyond thermal cloaks and thermal concentrators)for controlling/manipulating heat transfer,say,yielding the behavior of thermal transparency[6]when thermal conductivities depend on temperature or not.[18]Also,it is helpful for interdisciplinary researches on other kinds of gradation pro files when Laplace’s equation governs the system.[19?21]

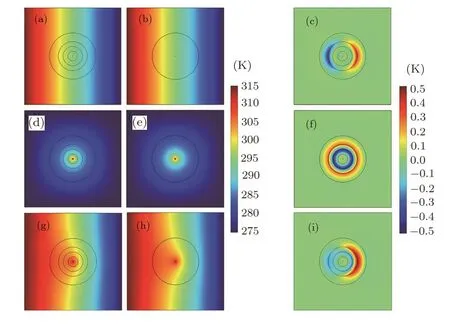
Fig.6 (Color online)Finite element simulations for self-heating multi-layer materials.In(a),(b),(d),(e),(g),(h),the thermal conductivity of the host medium is 300 W·m?1·K?1.In(a),(d),(g),the 4-layer structure is made of materials with thermal conductivity 300,275,390 and 275 W·m?1·K?1from inside-out.(a)A 4-layer material(without self-heating)subjected to a uniform density of heat flux;(d)a self-heating 4-layer material;(g)a self-heating 4-layer material subjected to a uniform density of heat flux.In(b),the homogeneous circle’s thermal conductivity(300 W·m?1·K?1)is equal to the effective thermal conductivity of the multi-layer material shown in(a)determined by Eq.(30);in(e),the homogeneous circle’s thermal conductivity(300 W·m?1·K?1)equals the effective thermal conductivity of the multi-layer material shown in(d)determined by Eq.(32);in(h),the homogeneous circle’s thermal conductivity(300 W·m?1·K?1)equals the effective thermal conductivity of the multi-layer material shown in(g)determined by either Eq.(30)or Eq.(32).(c),(f)and(i)display the temperature difference between(a)and(b),(d)and(e),and(g)and(h),respectively.

[1]C.Z.Fan,Y.Gao,and J.P.Huang,Appl.Phys.Lett.92(2008)251907.

[2]T.Chen,C.N.Weng,and J.S.Chen,Appl.Phys.Lett.93(2008)114103.

[3]J.Y.Li,Y.Gao,and J.P.Huang,J.Appl.Phys.108(2010)074504.

[4]S.Guenneau,C.Amra,and D.Veynante,Opt.Express 20(2012)8207.

[5]S.Narayana and Y.Sato,Phys.Rev.Lett.108(2012)214303.

[6]X.He and L.Z.Wu,Phys.Rev.E 88(2013)033201.

[7]R.Schittny,M.Kadic,S.Guenneau,and M.Wegener,Phys.Rev.Lett.110(2013)19590.

[8]T.Han,J.Zhao,T.Yuan,et al.,Energy Environ.Sci.6(2013)3537.

[9]T.Han,X.Bai,D.Gao,et al.,Phys.Rev.Lett.112(2014)054302.

[10]Y.Li,X.Y.Shen,Z.H.Wu,et al.,Phys.Rev.Lett.115(2015)195503.

[11]X.Y.Shen,Y.Li,C.R.Jiang,and J.P.Huang,Phys.Rev.Lett.117(2016)055501.

[12]X.Y.Shen,Y.X.Chen,and J.P.Huang,Commun.Theor.Phys.65(2016)375.

[13]Y.J.Xiang,S.C.Wen,X.Y.Dai,and D.Y.Fan,Phys.Rev.E 82(2010)056605.

[14]A.Acreman,M.Kaczmarek,and G.D’Alessandro,Phys.Rev.E 90(2014)012504.

[15]E.Reyes-Gomez,S.B.Cavalcanti,and L.E.Oliveira,Phys.Rev.E 91(2015)063205.

[16]L.Z.Wu,J.Heat Transfer 137(2015)021301.

[17]G.Q.Xu,H.C.Zhang,Q.Zou,and Y.Jin,Int.J.Heat and Mass transfer 109(2017)746.

[18]Y.Y.Li,N.B.Li,and B.W.Li,Eur.Phys.J.B 88(2015)182.

[19]L.Dong,G.Q.Gu,and K.W.Yu,Phys.Rev.B 67(2003)224205.

[20]L.Dong,J.P.Huang,K.W.Yu,and G.Q.Gu,Eur.Phys.J.B 48(2005)439.

[21]C.Z.Fan,Y.H.Gao,Y.Gao,and J.P.Huang,Commun.Theor.Phys.53(2010)913.