Numerical Study of Mixed Convective Peristaltic Flow through Vertical Tube with Heat Generation for Moderate Reynolds and Wave Numbers

Tariq Javed,B.Ahmed,and M.Sajid

Department of Mathematics and Statistics,International Islamic University,Islamabad 44000,Pakistan

1 Introduction

Recently many researchers and scientists have shown deep interest in fluid mechanics due to its application in numerous fields.There are certain fluid models in the fluid mechanics that has gained considerable importance in engineering and biomedical science.With all these models,peristalsis is one of most important and divest mechanism for transportation of fluid. Mixing and transportation of physiological fluids obey the peristaltic theory,which follows the progressive wave’s expansion and contraction along the length of the distensible tube that transportfluid.The mechanism is based on mainly neuromuscular property of tabular smooth muscle structure.Fixed speed and wavelengths are the main features of this kind of muscular tube.The phenomena can be found in the transportation of urine,movement of chyme,biologicalfluids in the lymphatic vessel and movement of bile.The peristaltic mechanism also finds in many application in bio-medical equipment and engineering like in designing of roller and finger pump,a heart-lung machine,a blood pump and dialysis machine.

The pioneer work was done by Latham,[1]he was thefirst who gives the mathematical approach to observe peristalsis flow in his master thesis.A number of articles[2?10]addressing the peristaltic phenomenon for a different type of geometries under the assumption of long wavelength and low Reynolds number,small amplitude ratio and wave number are available.The lubrication theory was used by Shapiro et al.[11]to investigate the peristaltic transportation of fluid in the two-dimensional channel using a wave frame of reference.On the other hand,Fung&Yih[12]used the fixed frame of reference for investigation of peristaltic flow without using lubrication approach.The nonlinear terms get vanished through the approach by Shapiro et al.[11]and the problem becomes simpler in comparison to that of Fung and Yih[12]approach.In this way,effects of Reynolds number and wave number(rate of the characteristic length of the tube to the wavelength of the peristaltic wave)on various flow characteristics cannot be investigated.Due to the simplicity of the approach,this theory is used widely to study the peristaltic flow of Newtonian and non-Newtonian fluid in a number of scenarios.Jaffrin[13]discussed the perturbation solution of two-dimensional peristaltic flow in a channel. Zien and Ostrach[14]also discussed the peristaltic mechanism.Takabatake and Ayukawa[15?16]employed the finite difference method to numerically simulate two-dimensional peristaltic flow in a channel for moderate values of the Reynolds number and wave number.They showed the perturbation solution of Jaffrin.[13]Zien and Ostrach[14]presented the result in a narrow range and in accordance with Reynolds number,the reflux phenomenon does not cause the change of the whole situation in the flow.The application of immersed boundary technique to simulate the transport,solid particle in a two-dimensional channel by peristalsis was initiated by Fouci.[17]Mekheimer[18]discussed the magnetohydrodynamic effect in the natural limitation of the peristaltic phenomenon,which is not valid for moderate values of both Reynolds number and wave number. Peristaltic flow and heat transfer effect under the long wavelength assumption in a vertical annulus is reported by Vahravelu et al.[19]They conclude that heat transfer at the peristaltic wall has significantly affected by the amplitude of the wave.Mekheimer and Elmabond[20]studied Newtonian peristaltic flow with the effect of heat transfer and MHD in the vertical annulus by using low Reynolds number and long wavelength assumption.They conclude that the trapping bolus increases by increasing the heat observation and generation parameter.Srinivas and Kathandapani[21]discussed the mechanism of peristalsis passing through porous medium supported by compliant walls.They compared the heat and mass transfer and noticed that heat effects are more dominant in the straight channel as compared to that in the curved channel in presence of applied magnetic field.Ramesh[22]recently studied the peristaltic flow in slip and convective condition through a porous medium.He solved his problem after making simplification with the help of lubrication theory.Recently Javed et al.[23]solved the peristaltic problem using finite element method in a porous medium.They found that their obtained results using finite element technique are in accordance with that of Jaffrin.[13]They conclude that the trapping bolus increases by increasing the heat generation parameter.Sajid et al.[24]investigated the mixed convective heat transfer on stretching sheet for an Oldroyd-B fluid.Barletta et al.[25]studied the heating and convection effects with a rapid variation of magnetic effects in a vertical annulus.Peristaltic flow under the influence of radially varying magnetic effects in a tube for Jeffrey fluid was studied by Abd-Alla et al.[26]Afsar et al.[27]presented the effect of variable viscosity in a porous medium for peristaltic transportation of Jefferyfluid.Recently Ahmed et al.[28]studied mixed convective peristaltic flow with heat generation in vertical channel and concluded that increase in heat generation resists the velocity in the central region while improves velocity in the vicinity of the peristaltic wall.

Most of the available studies on peristaltic flow are based on the assumptions of long wavelength and low Reynolds number,small amplitude ratio,and wave number.However,all such studies are developed in connection with the function of organs of the human body and there the Reynolds number associated with the flow is very low.[29?30]But this is not the case in the flows related to engineering field such as transport of blood,slurries and corrosive fluids by means of peristaltic pumps.In such flows there arise a need to analyze peristaltic flow at moderate Reynolds number.[31?32]The objective of the present study is to investigate numerical solution of mixed convective heat transfer in peristaltic flow passing through a vertical tube for non-zero Reynolds and wave numbers in presence of heat generation.Firstly,we derive the governing equations and convert them in dimensionless form by using appropriate dimensionless quantities.Secondly,by introducing the stream function,we convert the system of equations in stream-vorticity form and then expose to Galerkin’s finite element method,which allows computation of vorticity directly instead of being obtained by differentiation of the velocity field.The solution obtained by this formalism is utilized to illustrate the effects of moderate Reynolds number and wave number on various features of peristaltic motion.

2 Mathematical Modeling

Consider the motion of the Newtonian fluid through a vertical tube having inner width size 2d.The flow is assumed in such a way that the propagation of waves is along the z-axis with velocity c and r is normal to the tube.The peristaltic wall of the channel are assumed at temperature T1and obey the sinusoidal wave shape given by

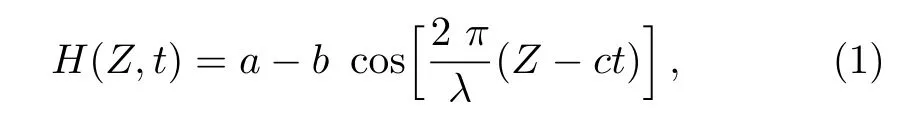
Fig.1 Geometry of the peristaltic flow in the tube.

where a represents mean distance of wall from central axis,λ is wavelength and b corresponds to wave amplitude.The schematic flow diagram is presented in Fig.1.The partial differential equations correspond to considered model of peristaltic flow in a fixed frame are

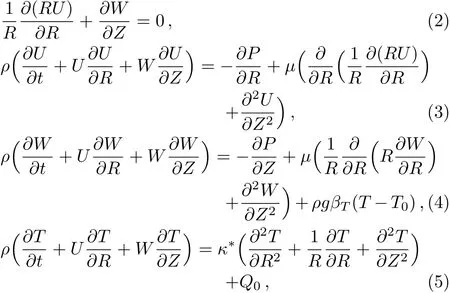
in whichμ is viscosity,ρ is density,g is acceleration due to gravity,βTcoefficient of thermal expansion,κ?is thermal conductivity and Q0is the constant heat generation within the flow domain.The boundary conditions of the problem are

The conversion between lab frame and wave frame are presented as follows

where z?and r?are component of velocity in axial and radial directions in moving frame of reference and(Z,R)is the corresponding velocity vector in laboratory frame.The following boundary condition are used to flow the moving frame

where ψ?denotes stream function.The flow rate in wave frame is related to time-mean flow in lab frame by the expression q?=Q??cH2.Inserting following dimensionless variables to the system,

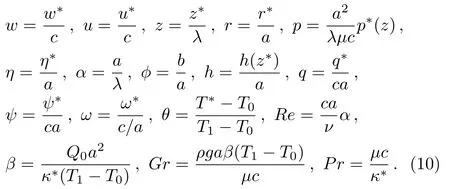
After eliminating the pressure gradient term from governing equations of momentum,the combined momentum equation with temperature and vorticity equation in stream function(by introducing u= ?(α/r)?ψ/?z and w=(1/r)?ψ/?r)becomes

where

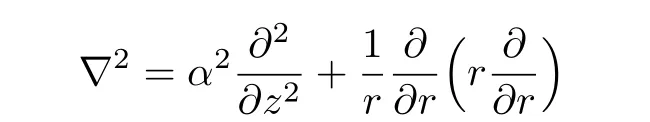
and modified Laplacian D2is define as

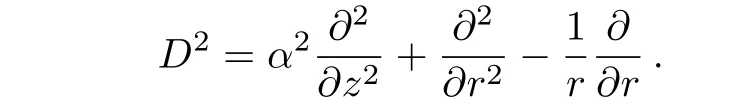
The boundary conditions for considered flow field become

3 Numerical Analysis

In this section,we presented a numerical solution of Eqs.(11)to(13)under the constraints of boundary conditions given in Eq.(14).By neglecting the assumption of long wavelength and low Reynolds number,we arrive ourself to a system of nonlinear partial differential equations equipped with the complex geometry of peristaltic tube.Thus,we need an efficient and rapid convergent technique to control such type of complicated problem.So the method based on Galerkin’s weighted residual based finite element technique is implemented by discretizing the domain in a subdomain of six nodal quadratic triangular elements to get the highly convergent results with a tolerance of 10?14which is achieved in a maximum 4-6 number of iterations.The stream function,vorticity and temperature approximated as

where ψk,ωk,and θkare approximation of ψ,ω,and θ respectively.The Galerkin’s based finite element is applied to Eqs.(11)to(12)gives as

where w1,w2,and w3are weight functions and d?=2πrdrdz.Simplifying Eqs.(16)to(18),we get

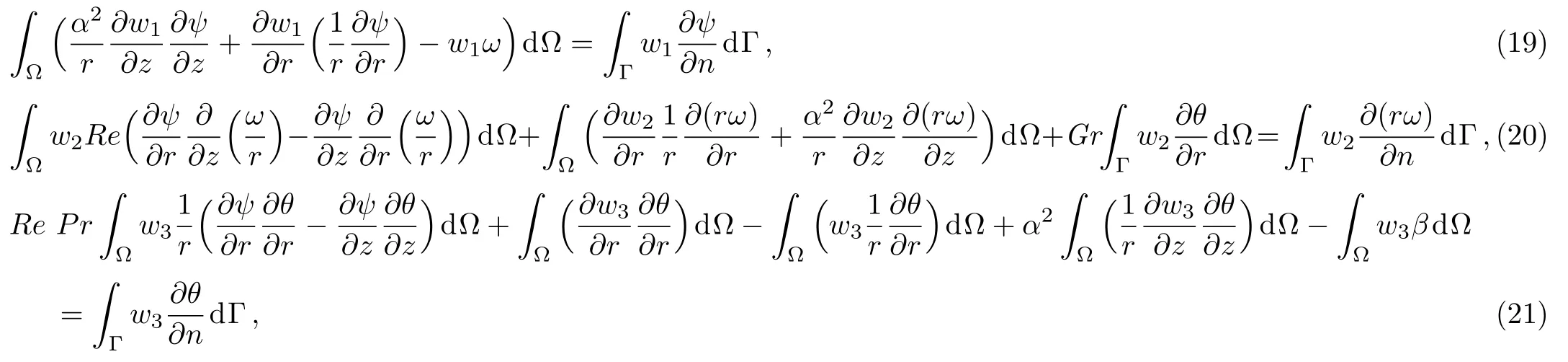
where dΓ=πrdrdz.Introducing Eq.(15)into Eqs.(19)to(21)and considering the discretized domain,we have

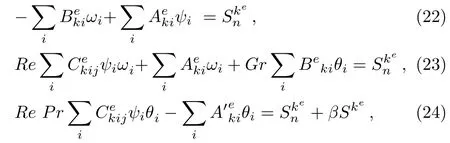
where

The global system of elements in matrix form is

in which

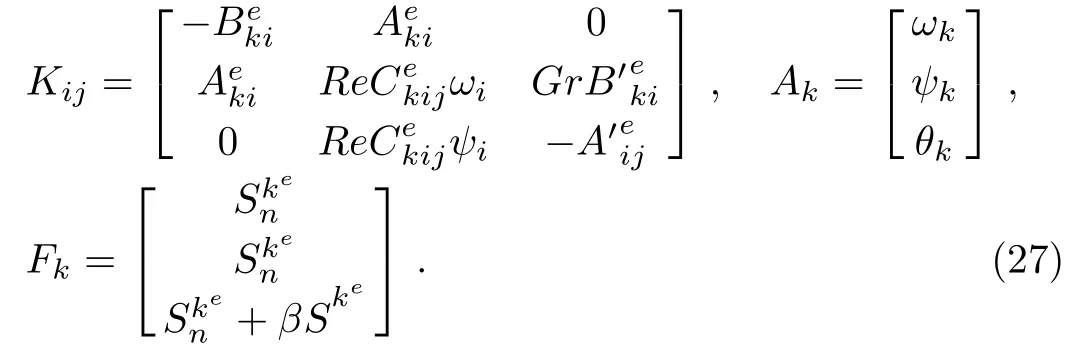
Pressure rise per wavelength plays a vital role in the peristaltic flow.In order to determine the pressure within a tube,it is sufficient to determine it at the middle portion of the wave.Rise in pressure per wavelength is given by

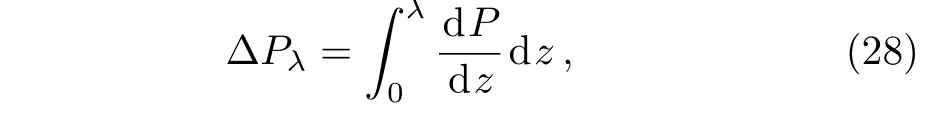
wheredP/dzisdirectly determined through nondimensional Naiver-Stokes equation.

4 Results and Discussion

For the moderate finite values of Reynolds number,a theoretical analysis of the peristaltic flow is extremely difficult because of the nonlinearity in the modeled equations,which occurs by the interaction of moving wall and the flow field. The effects of Reynolds number along with other interesting parameters involved in the modeled equation are studied by plotting the velocity distribution,temperature pro file,and pressure rise per wavelength.The contours of streamlines and vorticity are plotted with the detailed discussion is provided.

4.1 Validation

This section is dedicated for authentication of our own build MATLAB code of finite element method,which gives the numerical solution of a modeled system of nonlinear partial differential equations.Mekheimer and Abd elmaboud[29]gave results of heat transfer on peristaltic transport in the vertical tube by using assumptions of lubrication theory.These results are purely analytical and hence considered to be a benchmark solution in this comparison.The obtained results of pressure distribution are compared with the results of Mekheimer and Abd elmaboud[28]in limiting case by showing both results in Fig.2(a).

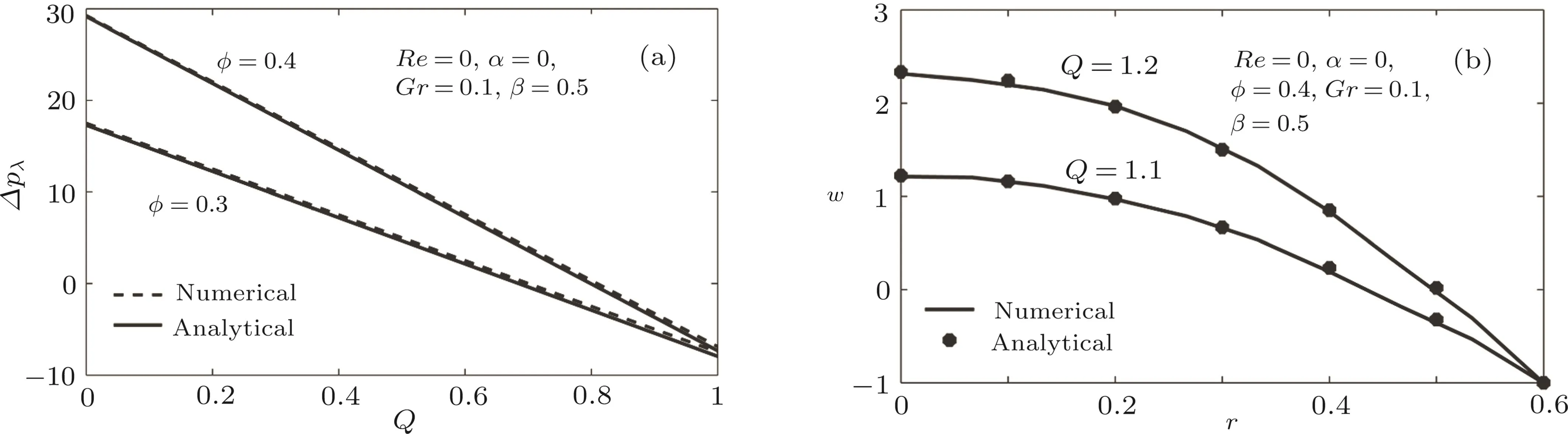
Fig.2(a)Comparison of pressure distribution for present numerical results with analytical results of Mekheimer and Abd elmaboud;[33](b)Comparison of longitudinal velocity for present numerical results with analytical results of Hameed,et al.[34]

The graphs presented in Fig.2(a)exhibits good agreement with our results under assumptions of long wavelength and low Reynolds number(for Re=0,α=0)with corresponding results of Mekheimer and Abd elmaboud.[29]The graphs of longitudinal velocity are also plotted in limiting case of obtained results to compare with the results of Hameed et al.[30]in Fig.2(b).Figure 2(b)shows good agreement with obtained numerical results with results that of Hameed et al.[30]with long wavelength and low Reynolds number assumption.

4.2 Velocity Pro file

To analyze the behavior of the velocity,longitudinal velocity is plotted at cross-section z=0 for various values of participated parameters such as Reynolds number Re,wave number α,Grashof number Gr,Prandtl number Pr,heat generation parameter β,and volume flow rate Q.In Fig.3,we presented the effect of Reynolds number Re on velocity distribution.We see that near the center of the tube,increase in Re causes a decrease in velocity while an opposite behavior is observed at the wall.It predicts that dominant inertial effects to viscous forces in the center of the tube causes decrease in velocity of the fluid,while near the wall,increase in inertial forces enhances the velocity.The same but clearer trend is observed by the velocity by varying the wave number at fixed values of other parameters as shown in Fig.4.It is also observed that for large values of wave number,the velocity attains its maximum value before entering in the region of r=0.It is also interesting to note that longitudinal velocity is less sensitive to the values of Reynolds number in the range 0.2≤ r≤ 0.4.Similarly,longitudinal velocity varies slowly with wave number in this range and after its rapid change is observed.In Fig.5,we observed that the velocity increases in the vicinity of the peristaltic wall by enhancing Grashof number and drops near the center of the tube.It is noted from Figs.6 to 8 that velocity pro file becomes concave shape for Reynold number,Prandtl number,and Grashof number.It is also observed that for Grashof number,change in velocity behavior is much faster in comparison with that of Reynold number and Prandtl number.It concludes that due to increase in the temperature,the velocity of the fluid decreases and consequently more resistance appears in the flow field.We observe that when time-mean flow rate Q≤1,the velocity pro file becomes negative and fluid particle at r=0 moves to opposite direction of the flow field.When time-mean flow rate Q>1,theflow becomes positive and fluid particle moves in the direction of the flow field.It concludes that the particle moves along the direction of the flow field when Q>1.

Fig.3 Longitudinal velocity for various values of Reynolds number Re.

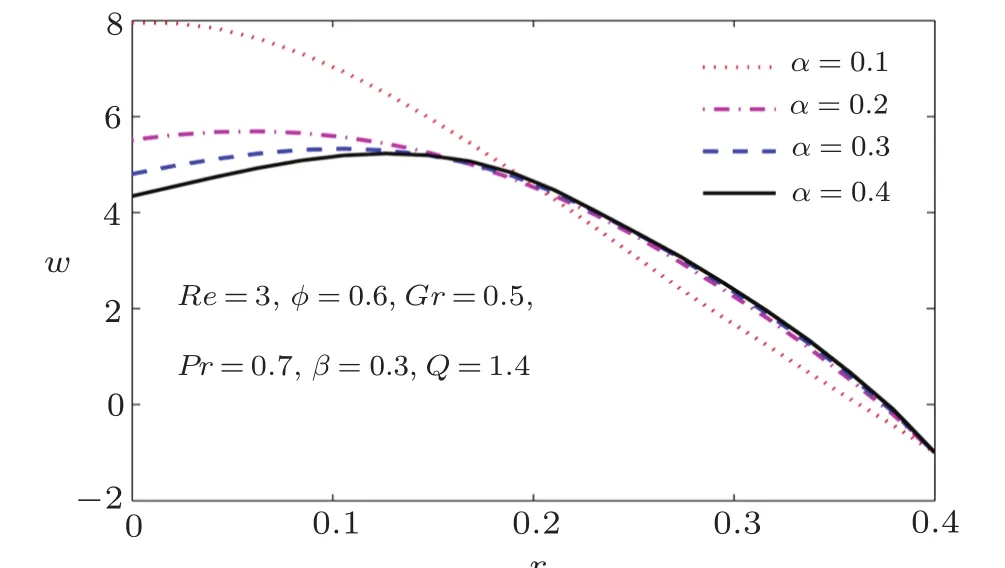
Fig.4 Longitudinal velocity for various values of wave numbers α.

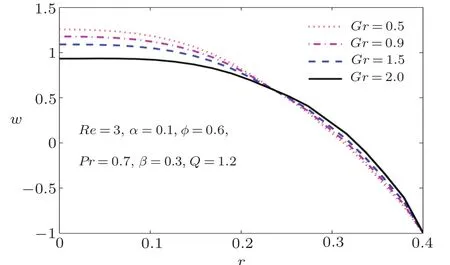
Fig.5 Longitudinal velocity for various values of Grashof number Gr.

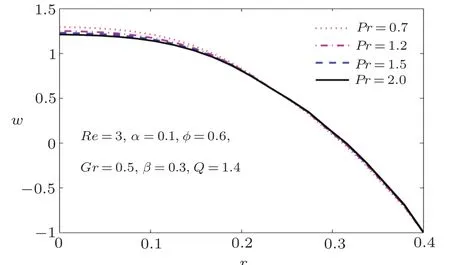
Fig.6 Longitudinal velocity for various values of Prandtl number Pr.

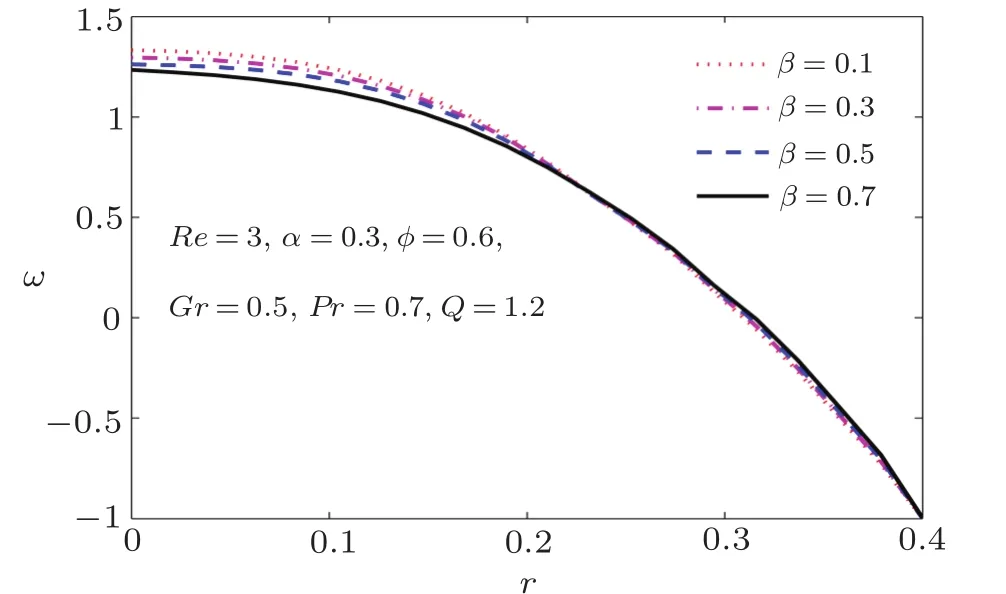
Fig.7 Longitudinal velocity for various values of heat generation parameter β.

Fig.8 Longitudinal velocity for various values of time-mean lf ow rate Q.

4.3 Temperature Distribution

Figures 9 to 14 are sketched to present and study the physical effects of all embedded parameters on temperature pro file.The first time in the literature,the effects of Reynolds number Re are presented for temperature distribution in Fig.9,as long wavelength and low Reynolds number theory is not able to predict such non-linear effect.It shows strong inertial induced by large values of Reynolds number in whole region of the tube.The opposite behavior for variation of wave number α are presented in Fig.10.

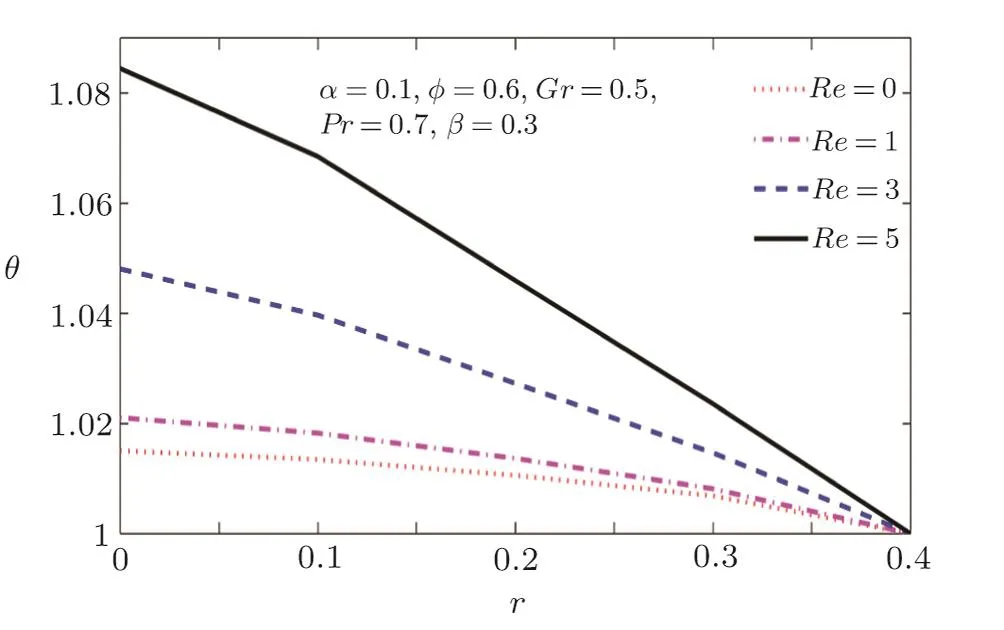
Fig.9 Temperature pro file for various values of Reynolds number Re.

Fig.10 Temperature pro file for various values of wave number α.

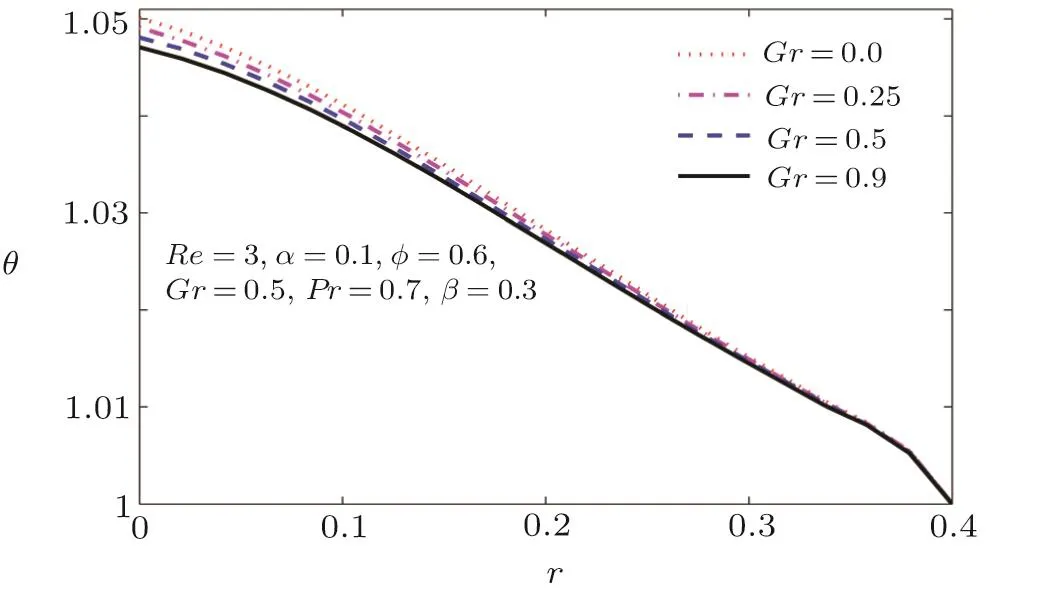
Fig.11 Temperature pro file for various values of Grashof number Gr.

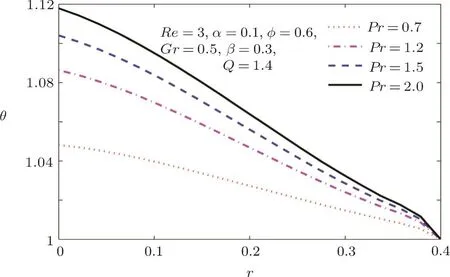
Fig.12 Temperature pro file for various values of Prandtl number Pr.

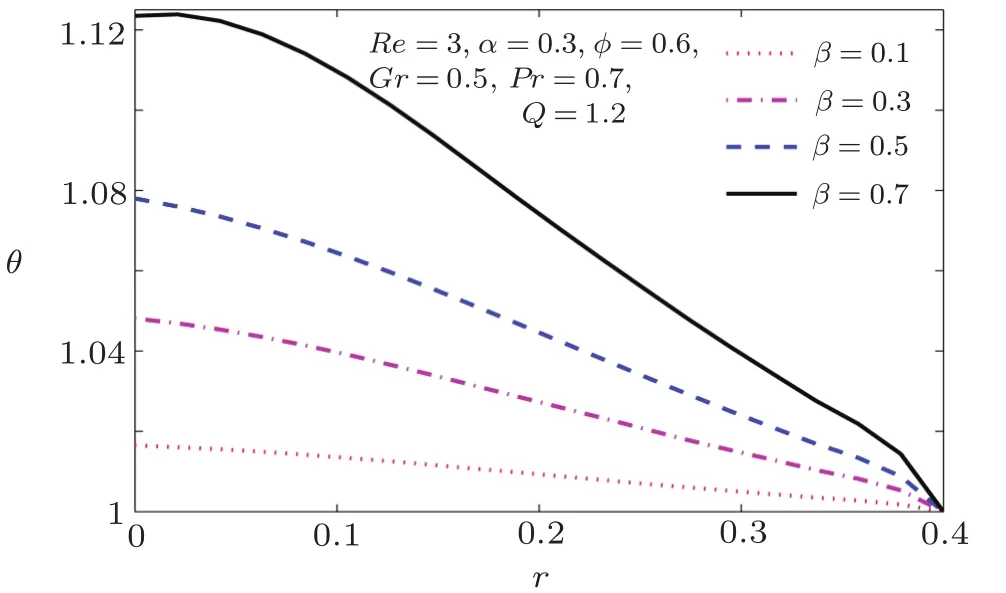
Fig.13 Temperature pro file for various values of heat generation parameter β.

Fig.14 Temperature pro file for various values of time-mean lf ow rate Q.

Figure 11 shows that increase in Grashof number Gr by increasing the effect buoyancy forces as compared to viscous forces has an important role in reducing the temperature of the fluid with in the tube.Figure 12 shows that temperature of the fluid can be enhanced by increasing the Prandtl number.The temperature increases when the convective heat is enhanced which is evident from Fig.13.Figure 14 shows that the increase in time-mean flow rate enhances the internal energy of the fluid and consequently increase in temperature is noted.

4.4 Pressure Distribution

The purpose of this subsection is to examine important phenomena of pressure rise per wavelength in peristaltic transportation.Usually,the three ranges of pumping in peristalsis are possible,?P<0 corresponds to augmented pumping region while?P=0 is the free pumping region and?P>0 is for co-pumping region.We have presented only first?P>0 which are of most interest for engineering and have vastly applicable in bio-medical sciences.Figure 15 reveals the effect of variation of Reynolds number Re on pressure rise per wavelength.It is observed that in the absence of inertial forces(for Re=0),the linearity in the graph is observed and shows non-linear trend for the non-zero inertial forces.Furthermore,it is noted that the increase in pressure rise by dominating inertial forces to the viscous forces,which are made by increasing the values of the Reynolds number.So Reynolds number exhibits the direct relation with pressure rise per wavelength.The same behavior is shown by wave number in Fig.16.This is due to the fact that by an increase in wave number,the fluid passes through the tube with increased width,which causes an increase in pressure.Figure 17 gives us an idea about ? P against Q with variation in heat generation parameter β.Due to increase in the generation of the heat,internal energy of the fluid increases and consequently enhancement in pressure rise per wavelength is noted as shown in the figure.Figure 18 is plotted to examine the dimensionless quantity Grashof number Gr defined in equation has been used in the analysis of the pressure.It is noted that most rapid and remarkable increase in pressure rise is observed with the increase in Grashof number as compared to that of increase in heat generation.

Fig.15 Pressure rise against time-mean flow rate Q for various values of Reynolds number Re.

Fig.16 Pressure rise against time-mean flow rate Q for various values of wave number α.

Fig.17 Pressure rise against time-mean flow rate Q for various values of heat generation parameter β.

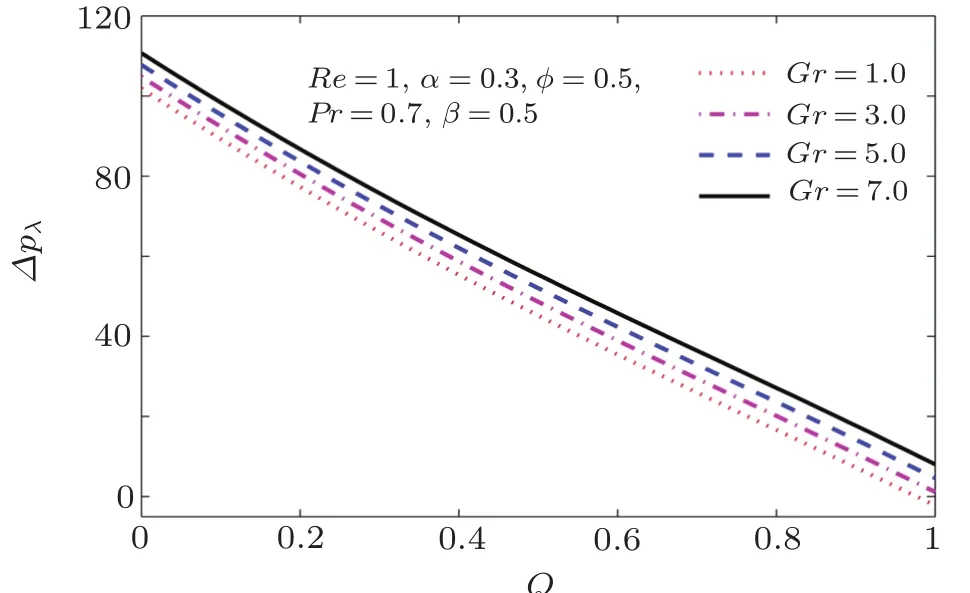
Fig.18 Pressure rise against time-mean flow rate Q for various values of Grashof number Gr.

4.5 Trapping Phenomena

The phenomena based on the circulation of the streamlines known as trapping.Trapping is an interesting mechanism for peristaltic flows to discuss the flow properties under the influence of parameters involved in the model.We discuss this phenomenon in Figs.19 to 22.

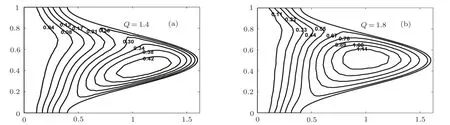
Fig.19 Streamlines for various values of time-mean flow rate Q with fixed values of the parameter Re=1,α =0.1,? =0.6,Pr=0.7,β=0.3,Gr=0.5.

Fig.20 Streamlines for various values of Reynold numbers Re with fixed values of the parameter α =0.1,? =0.6,Pr=0.7,β=0.3,Gr=0.5,Q=1.4.

Figure 19 shows the effect of different values of time mean flow rate on the fluid flow.It has been observed that augmentation in the time mean flow rate causes reduction in size of the bolus.This is due to the increase in smoothness in the movement of the fluid in the central region of the tube.Figure 20 shows that the increase in Reynolds number,the flow becomes smoother in the central region.Furthermore,increases the number of the trapped boluses is noted with a cluster of bolus shows tendency to move in the upper region of the crest.The same behavior is observed in case of wave number α as shown in Fig.21.It also reflects that we can control the smoothness of the movement of the fluid in central part of the tube.In Fig.22,we have increase the Grashof number Gr from 0.1 to 0.9(where vanishing buoyancy effects corresponds to the Newtonian case as reported by Shapiro et al.[11])It is noted that magnitude of the trapped bolus reduces and moves in region near the wall of tube.

Fig.21 Streamline for various values of wave numbers α with fixed values of the parameter Re=1.0,? =0.6,Pr=0.7,β=0.3,Gr=0.5,Q=1.4.

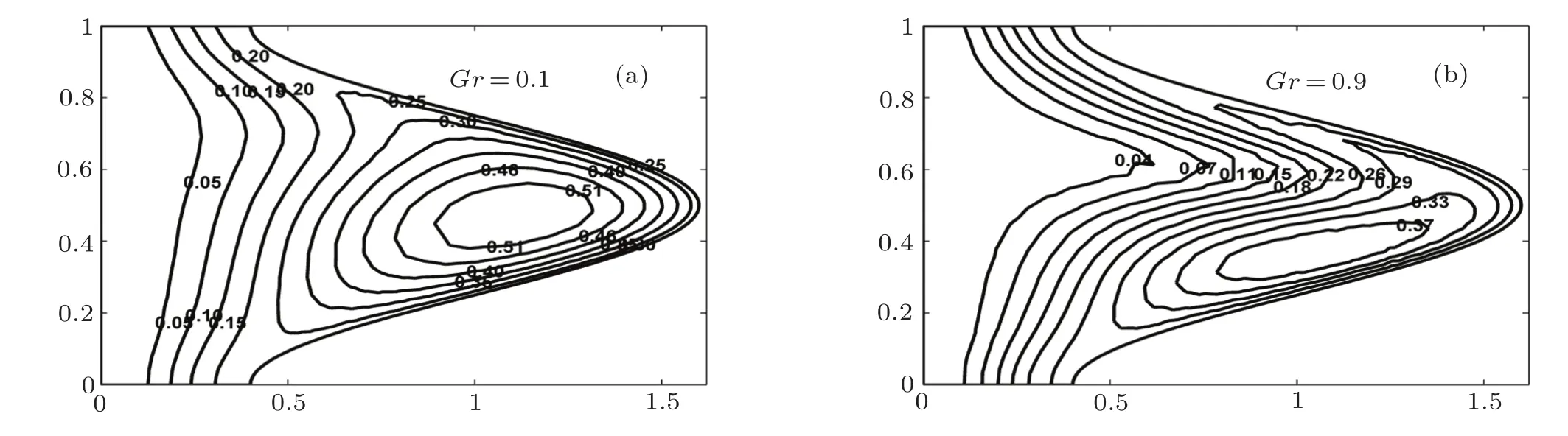
Fig.22 Streamline for various values of Grashof number Gr with fixed values of the parameter Re=1.0,α =0.1,? =0.6,Pr=0.7,β=0.3,Gr=0.5,Q=1.4.

4.6 Isothermal Lines

Isothermal lines are representation of the temperature distribution in a flow field.The sketches of isothermal lines for different parameters are presented in Figs.23 to 27.Figure 23 presents the isothermal lines for time-mean flow rate Q=1.2 and Q=1.8.We observe the symmetric behavior for small values of Q while large values of Q increase in concentration of the isothermal lines to the lower part of the central region of the tube.For small values of the Reynolds number Re,the strong tube as we increase the Reynolds number,concentration of temperature is reduced in the upper region of the tube which can be seen by temperature distribution have been observed in the whole wavy region of the absence of isothermal lines in that region in Fig.24.

Fig.23 Isothermal lines for various values of time-mean flow rate Q with fixed values of the parameter Re=1,α=0.1,? =0.6,Pr=0.7,β =0.3,Gr=0.5.

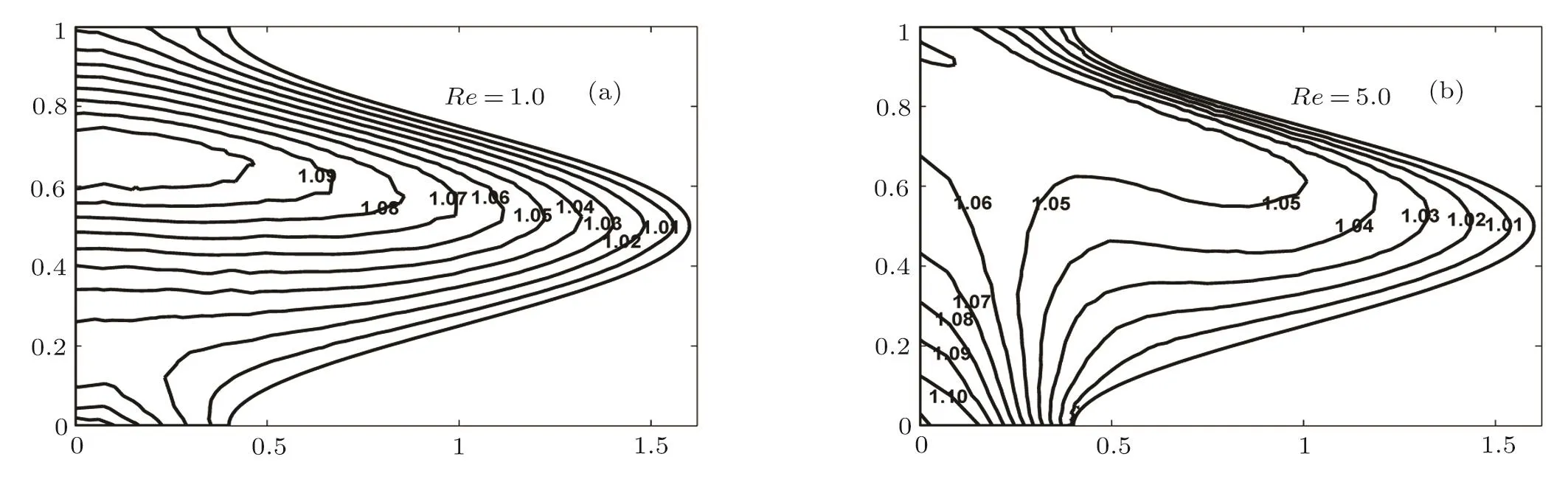
Fig.24 Isothermal lines for various values of Reynold numbers Re with fixed values of the parameter α =0.1,? =0.6,Pr=0.7,β=0.3,Gr=0.5,Q=1.4.

Fig.25 Isothermal lines for various values of wave number α with fixed values of the parameter Re=1.0,? =0.6,Pr=0.7,β=0.3,Gr=0.5,Q=1.4.

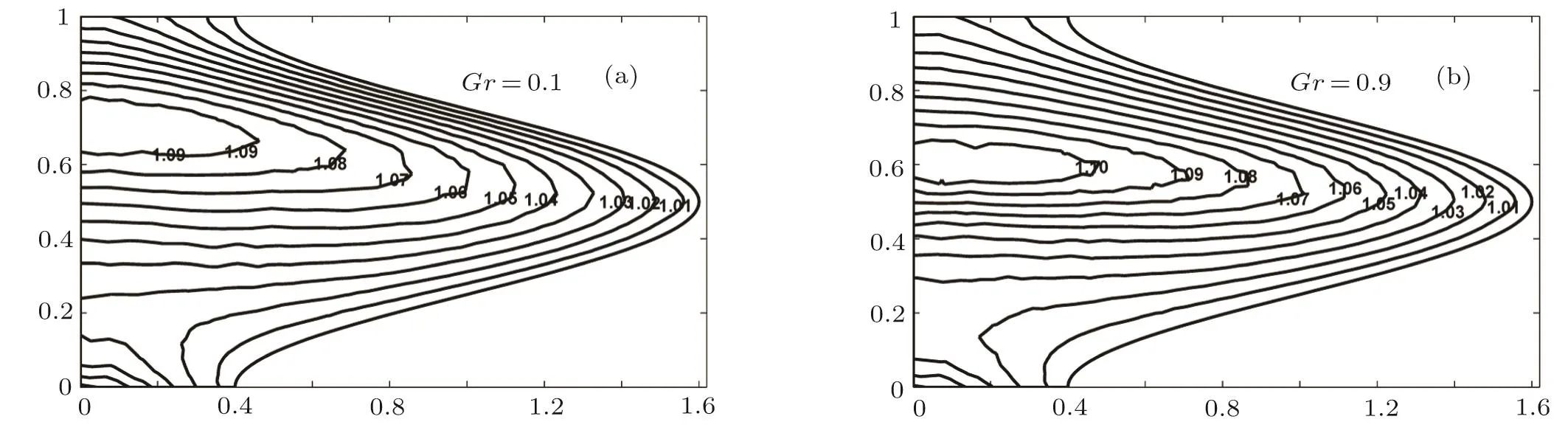
Fig.26 Isothermal lines for various values of Grashof number Gr with fixed values of the parameter Re=1.0,α=0.1,? =0.6,Pr=0.7,β =0.3,Gr=0.5,Q=1.4.

The effects of the wave number α on isothermal lines are shown in Fig.25.It is observed that values of wave number creates the symmetric like trend of isothermal lines and the isothermal lines for different Grashof number Gr are shown in Fig.26,which indicates that increase in Grashof number enhances the movement of isothermal lines to the crest region of the peristaltic wall.The increase in heat capacity of the fluid flow in the peristaltic transport model increases the number of isothermal lines in the center of the tube and enhances in the narrow part of the tube as represented by the plots of isothermal lines for Prandtl number Pr in Fig.27.

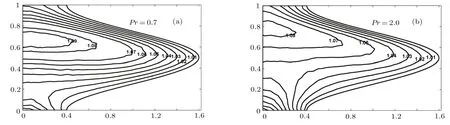
Fig.27 Isothermal lines for various values of Prandtl numbers Pr with fixed values of the parameter Re=1.0,α=0.1,? =0.6,β =0.3,Gr=0.5,Q=1.4.

5 Conclusion

The numerical results of streamlines and temperature distribution for mixed convective peristaltic flow passing through the vertical tube are studied and shown graphically with a suitable set of values of involved parameters by using finite element method.The key features of this study are as follows:

(i)At the center of the tube,increasing values of Reynolds number decreases the velocity while increases the temperature but increasing wave number enhances the velocity and reduces the temperature.

(ii)The decrease in velocity is noted at center for increasing values of Grashof number,Prandtl number and heat generation parameters,while the slight increase is also noted away from the center.

(iii)For values of time-mean flow less than 1,velocity pro file becomes negative at z=0 cross section and for values greater than 1 it becomes positive.

(iv)The decrease in temperature is noted for increasing values of Grashof number while Prandtl number,heat generation and time-mean flow rate supported in raising the temperature.

(v)Pressure rise per wavelength can be enhanced by increasing the both Reynolds number and Grashof number.Also,a decrease in pressure rise is observed by increasing values of wave number and heat generation parameter.

(vi)Increase in size and number of bolus for contours of streamlines are noted for an increase in Reynolds number and wave number while disturbance is reported for increasing Grashof number.By increasing Reynolds number,isothermal lines move along peristaltic wall and concentration in a lower part of the center of tube increases.

(vii)The symmetry of isothermal lines are disturbed and saturation in the lower part is reported by increasing time-mean flow rate.Also,isotherms are generated on peristaltic wall and move towards the center of the tube by increasing wave number,Grashof number and Prandtl number.

[1]T.W.Latham,Fluid Motions in a Peristaltic Pump,Diss.Massachusetts Institute of Technology(1966).

[2]S.L.Weinberg,E.C.Eckstein,and A.H.Shapiro,J.Fluid Mech.49(1971)461.

[3]H.S.Lew,Y.C.Fung,and C.B.Lowenstein,J.Biomech.4(1971)297.

[4]B.V.R.Kumar and K.B.Naidu,Comput.Fluids 24(1995)161.

[5]M.J.Manton,J.Fluid Mech.68(1975)467.

[6]M.Y.Jaffrin,Int.J.Eng.Sci.11(1973)681.

[7]D.Tripathi,Math.Comput.Model.57(2013)1270.

[8]T.K.Hung and T.D.Brown,J.Fluid Mech.73(1976)77.

[9]M.Narahari and S.Sreenadh,Int.J.Appl.Math.Mech.6(2010)41.

[10]A.R.Rao and S.Usha,J.Fluid Mech.85(1995)298.

[11]A.H.Shapiro,M.Y.Jaffrin,and S.L.Weinberg,J.Fluid Mech.37(1969)799.

[12]Y.C.Fung and C.S.Yih,J.Appl.Mech.35(1968)669.

[13]M.Y.Jaffrin,Int.J.Engin.Sci.11(1973)681.

[14]T.F.Zein and S.A.Ostrach,J.Biomech.3(1970)63.

[15]S.Takabatake,K.Ayukawa,and M.Sawa,Trans.JSME-An Int.J.53 (1987)1207,doi.org/10.1299-/kikaib.53.1207.

[16]S.Takabatake,Trans.JSME-An Int.J.56(1990)3633,doi.org/10.1299/kikaib.56.3633.

[17]Lisa J.Fauci,Comput.Fluids 21(1992)583.

[18]Kh.S.Mekheimer,Int.J.Appl.Math.Artical ID:570825(2008),doi:10.1155/2008/570825.

[19]K.Vajravelu,G.Radhakrishnamacharya,and V.Radhakrishnamurty,Int.J.Nonlinear Mech.42(2007)754.

[20]Kh.S.Mekheimer and Y.Abd Elmaboud,Appl.Math.Inform.Sci.2(2008)103.

[21]S.Srinivas,R.Gayathri,and M.Kothandapani,Commun.Nonlinear Sci.16(2011)1845.

[22]K.Ramesh,Comput.Meth.Prog.Bio.135(2016)1.

[23]T.Javed,B.Ahmed,N.Ali,and A.H.Hamid,J.Porous Media 20(2017)841.

[24]M.Sajid,B.Ahmed,and Z.Abbas,J.Egypt.Math.Soc.23(2015)440.

[25]A.Barletta,S.Lazzari,E.Magyari,and I.Pop,Int.J.Heat Mass Tran.51(2008)5777.

[26]A.M.Abd-Alla,S.M.Abo-Dahab,and A.Kilicman,J.Magn.Magn.Mat.384(2015)79.

[27]A.Afsar Khan,R.Ellahi,and K.Vafai,Adv.Math.Phys.2012(2012).

[28]B.Ahmed,T.Javed,A.H.Hamid,and M.Sajid,J.Appl.Fluid Mech.20(2017)1813.

[29]H.S.Lew,Y.C.Fung,and C.B.Lowenstein,J.Biomech.4(1971)297.

[30]Riahi,N.Daniel,and R.Ranadhir,Appl.Appl.Math.6(2011)428.

[31]S.Takabatake and K.Ayukawa,J.Fluid Mech.122(1982)439.

[32]T.Hayat,Y.Wang,K.Hutter,et al.Math.Probl.Eng.4(2004)347.

[33]Kh.S.Mekheimer and Y.Abd Elmabound,Phys.Lett.A.372(2008)1657.

[34]M.Hameed,A.A.Khan,R.Ellahi,and M.Raza,Engineering Science and Technology,an International Journal 18(2015)496.