數(shù)學(xué)通報2017年10月問題2387的另證及推廣

陜西省岐山縣蔡家坡高級中學(xué)(722405)公寬讓

《數(shù)學(xué)通報》2017年10月號問題2387設(shè)a,b,c≥0,a+b+c=6,求證:

證法1 (反證法)當(dāng)a,b,c＞0時,假設(shè)原不等式(1)不成立,即

結(jié)合已知a+b+c=6,由冪平均不等式

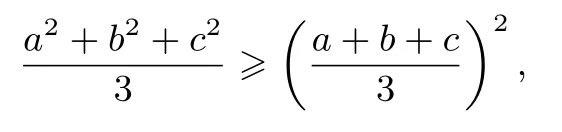
得a2+b2+c2≥12,從而有a2+6+b2+6+c2+6≥30,可見

不大于等于9,而由柯西不等式知

兩結(jié)論矛盾,所以假設(shè)錯誤,不等式(1)成立.

當(dāng)a,b,c中有一個為0時,同法可證明不等式(1)成立;

當(dāng)a,b,c中有兩個為0,一個為6;或a=b=c=2時,不等式(1)等號成立.

綜上,不等式(1)成立.

證法2 (放縮法)不妨設(shè)a≥b≥c≥0,則

由a+b+c=6,知2≤a≤6,當(dāng)a=2時,

所以

即不等式(1)成立.

問題2387按元數(shù)推廣如下:

定理1 設(shè)則

問題2387按元數(shù)和指數(shù)推廣如下:

定理2 設(shè)m∈N?,則

下面用兩種方法只證明(3):

證法1 (反證法)當(dāng)xi＞0(i=1,2,···,n)時,假設(shè)原不等式(3)不成立,即兩結(jié)論矛盾,所以假設(shè)錯誤,不等式(3)成立.

當(dāng)xi(xi≥0,i=1,2,···,n)中有少于n-1個為0時,同法可證明知不等式(3)成立;

當(dāng)xi(xi≥0,i=1,2,···,n)中有n-1個為0,一個為2n或x1=x2=···=xn=2時,不等式(3)等號成立.

綜上,不等式(3)成立.

證法2 (放縮法)取x0=max{xi(xi≥0,i=1,2,···,n)},則

即不等式(3)成立.

同樣用這兩種方法可證(2)成立,這里不再重復(fù).