On the Cycle Structure of Iteration Graphs over the Unit Group

JU Teng-xia,WU Mei-yun

(Faculty of Science,Nantong University,Nantong 226007,China)

On the Cycle Structure of Iteration Graphs over the Unit Group

JU Teng-xia,WU Mei-yun

(Faculty of Science,Nantong University,Nantong 226007,China)

In this paper,we consider the properties of iteration graphs over the unit group Z?nof the residue ring Znassociated with the maps x→xpand compute the average values of tails and cycles of those iteration graphs.

iteration digraph;tail;tree;cycle

§1.Introduction

A digraph is a f i nite set of vertices together with directed edges.The iteration digraph of a map f:S→S on a f i nite set S is a directed graph,whose vertices are elements of S and whose directed edges connect each x∈S with its image f(x)∈S.We denote such digraph by Gf.The iteration graphs of the function f(x)=xkon the residue ring S=Znprovided an interesting connection between number theory,graph theory and group theory and have been extensively discussed(see[1-5]).These digraphs ref l ect properties of Znand f.

Denote f0(x)=x and fi(x)=f(fi?1(x))for i≥1.Since S is f i nite,for each x∈S there exists a least positive integer s=s(x)such that fs(x)∈{f0(x),f1(x),···,fs?1(x)}.Let t=t(x)be the least non-negative integer such that fs(x)=ft(x).Setting c=c(x)=s(x)?t(x), we have ft(x)=ft+c(x).We call the list of elements x,f(x),f2(x),···,ft?1(x)the tail and ft(x),···,ft+c?1(x)the cycle.See Figure 1.

Figure 1The Tail and Cycle of an Iteration

Many natural questions are as follows:what are the average values of t(x)and c(x)over all elements x∈S?How many distinct cycles are there?What is their average size?What is the average tail length?

This paper extends some results given in[6]which computed the average values of t(x)and c(x)for the iteration digraph over the f i nite f i eld Zpassociated with maps f:x→x2and f:x→x2?2.We will compute the average values of tails and cycles of iteration graphs over the unit group Z?nof the residue ring Znassociated with the maps x→xp.

§2.The Iteration g:x→xp(mod n)

If H is a multiplicative group and x∈H,then ordHx means the least positive integer i such that xi=1.In the case that H=Z?n={1≤x≤n|(x,n)=1},the unit group of the residue ring Zn(the multiplicative group of invertible elements modulo n),we write ordnx.It is clear that Z?nis a group of order φ(n),where φ(n)is the Euler function.If p is a prime,and n is an integer,then by νp(n)we mean the exponent of the largest power of p which divides n.We def i ne νp(0)=+∞.One identity we will make use of frequently is Σd|nφ(d)=n.

A complete α-ary tree of height h,denoted Th,is a directed graph with αinodes at depth i,for 0≤i≤h,with the property that every non-leaf node has exactly α children.The graph Thcontainsnodes in total.

If G=(V,E)is a directed graph,then by GRwe mean the graph(V,ER),where ER:= {(x,y):(y,x)∈E}.We call GRthe reversed graph as in[6].

Theorem 2.1Let n≥3 be an integer and let S=Z?nand g:x→xp,where x∈S and p is an odd prime number.Suppose ordnx=pel,where e,l are non-negative integers with (p,l)=1.If t(x)is the length of the tail for the element x,and c(x)is the length of the cycle for x,as def i ned above,then t(x)=e=νp(ordnx)and c(x)=ordlp.

ProofIf gt(x)=gt+c(x),then we have xpt≡xpt+c(mod n).Hence for(x,n)=1 we have xpt(pc?1)≡1(mod n).We have pel|pt(pc?1),since ordnx=pel.By the def i nition of c and t,it follows that t=e=νp(ordnx),and that c is the least positive integer such that pc≡1(mod l),which means that c=ordlp.

We now recall the def i nition and some properties of the Carmichael λ-function λ(n)which was f i rst def i ned in[4].Let n be a positive integer.The Carmichael λ-function λ(n)is def i ned as follows:λ(1)=1=φ(1),λ(2)=1=φ(2),λ(4)=2=φ(4),λ(2k)=2k?2k≥3,λ(pk)=(p?1)pk?1=φ(pk)for any odd prime p and k≥1,

where p1,p2,···,psare distinct primes for ki≥1,i∈{1,···,s}and[a,b]denotes the least common multiple of numbers a and b.By this def i nition,λ(n)|φ(n).Let t=ordng denote the multiplicative order of g modulo n(that means t is the least natural number such that gt≡1(mod n)).

Lemma 2.2(Carmichael’s Theorem,See[7]and[8])Let a,n∈N.Then aλ(n)≡1(mod n)if and only if gcd(a,n)=1.Moreover,there exists an integer g such that ordng= λ(n).

Lemma 2.3(See Proposition 4.1.3 of[9])n possesses primitive roots if and only if n is of the form 2,4,pmor 2pm,where p is an odd prime and m is a positive integer.

We note that if n is of the form 2,4,pmor 2pm,where p is an odd prime and m is a positive integer,then λ(n)=φ(n),which means that if there exists a primitive root mod n, then λ(n)=φ(n).Next,we characterize the tails of elements in terms of primitive roots,as follows:

Theorem 2.4Let n≥3 be an integer such that there exists a primitive root modulo n, and let γ be a primitive root modulo n.Then

(a){a∈Z?n:t(a)=0}={γi:0≤i＜λ(n)and νp(i)≥νp(λ(n))};

(b)For 1≤m≤νp(λ(n)),we have{a∈Z?n:t(a)=m}={γi:0≤i＜λ(n)and νp(i)= νp(λ(n))?m}.

ProofSuppose a=γiand λ(n)=pτ·ω,where(p,ω)=1.

(a)We note that t(a)=0 means that the element a is in some cycle,i.e.,there exists l＞0 such that gl(a)=a and a≡apl(mod n).Then,t(a)=0 if and only if there exists l＞0 such that a≡apl(mod n).Note that in the case that there exists a primitive root mod n,λ(n)=φ(n). Then,a≡apl(mod n)if fapl?1≡1(mod n),if fγi(pl?1)≡1(mod n),if fλ(n)|i(pl?1),if f pτ|i and ω|i(pl?1)(since λ(n)=pτ·ω,(p,ω)=1,and(p,pl?1)=1),if fνp(i)≥τ and ω|i(pl?1).Thus t(a)=0 if fνp(i)≥νp(λ(n))and there exists l≥1 such that ω|i(pl?1).There always exists an l≥1 satisfying ω|pl?1,since(p,ω)=1.We may take l=ordωp,the result follows.

(b)Note that t(a)=m,1≤m≤νp(λ(n)),if fthere exists l＞0 such that apm≡apm+l(mod n)and apm-1≡apm+l-1(mod n),if fγipm(pl?1)≡1(mod n)and γipm-1(pl?1)/≡1(mod n),if fλ(n)|ipm(pl?1)and λ(n)? ipm?1(pl?1),if fω|i(pl?1)and pτ|ipm,but pτ? ipm?1.We have t(a)=m if fνp(λ(n))=νp(ipm)=νp(i)+m,if fνp(i)=νp(λ(n))?m.

Corollary 2.5Let n≥3 be an integer such that there exists a primitive root mod n and λ(n)=pτ·ω,where(p,ω)=1.For each positive divisor d of ω,Gx→xpcontains φ(d)/orddp cycles of length orddp and there are ω elements in all these cycles.Moreover

(1)If τ=0,then all elements are in cycles;

(2)If τ≥1,then of feach element in cycles there hang reversed complete p-ary trees of height τ?1 containing pτ?1 elements.

ProofBy Theorem 2.4,the elements x in the cycles are precisely of the form γi,where0≤i＜λ(n),νp(i)≥νp(λ(n))=τ and γ is a primitive root mod n.Set i=j·pτ,then 0≤j＜ω,since 0≤i＜λ(n)=ω·pτ.Hence there are ω elements in all cycles,which form a cyclic group of order ω with a generator γpτ.Hence for each divisor d of ω,there are φ(d) elements of order d,which are of the form γjpτω/d,where 0≤j＜d and(j,d)=1.

The length of the cycle for γjpτω/dis the least c such thatdj(pc?1)is an integer.Since (j,d)=1,c is the least positive number such that d|(pc?1),which means that c=orddp.It follows that there are φ(d)/orddp cycles corresponding to these elements.

Finally,suppose x≡γi(mod n)is an element with tail size t where,1≤t＜τ and the corresponding element y with tail size t+1 such that yp≡x(mod n).By the proof of Proposition 4.2.1 of[9],we know that if xm≡a(mod n)is solvable,there are exactly(m,φ(n))solutions. Then,there exist exactly α=(p,φ(n))distinct y.It is well-known that if there exists a primitive root mod n,then λ(n)=φ(n).Therefore,α=(p,φ(n))=(p,λ(n))=p or 1,since p is prime.

If τ=0,then ω=λ(n)and α=1,which means that all elements of Z?nare in cycles.

If τ≥1,then α=p.Since p?1+p(p?1)+···+pτ?1(p?1)=pτ?1,every p-nodes tree of height τ?1 contains pτ?1 elements.

Example 2.1Table 1 and Figure 2 illustrate Theorem 2.1 and Corollary 2.5 respectively in the case where n=13,p=3.When n=13,p=3,by computation,we have t(1)=t(12)= t(5)=t(8)=0,which means the numbers 1,12,5,8 are in cycles,since the length of their tail is 0.On the other side,the distance of numbers 3,9,4,10,2,6,7,11 from the cycle to which they are connected is 1.By computation of the value of c(x),it follows that the length of each cycle,which is connected to the numbers 1,12,3,9,4,10 respectively,is 1.But the length of each cycle,which is connected to the numbers 5,8,2,6,7,11 respectively,is 2. And of feach element in cycles there hang reversed 3-ary trees containing 2 elements(except the element in cycle).

Table 1The Structure of Gx→xpfor n=13,p=3.

>Figure2 The Topology of Gx→xpfor n=13,p=3.Figure 3 The Topology of Gx→xpfor n=27,p=3.

Example 2.2Table 2 and Figure 3 illustrate Theorem 2.1 and Corollary 2.5 in the case where n=27,p=3.When n=27,p=3,by computation,we have t(1)=t(26)=0,whichmeans the numbers 1,26 are in cycles,since the length of their tail is 0.On the other side, the distance of numbers 10,19,8,17 from the cycle to which they are connected is 1.While, the distance of numbers 4,7,13,16,22,25,2,5,11,14,20,23 from the cycle to which they are connected is 2.By the value of c(x),it follows that the length of each cycle,which is connected to each number respectively,is 1.And of feach element in cycles there hang reversed 3-ary trees containing 8 elements(except the element in cycle).

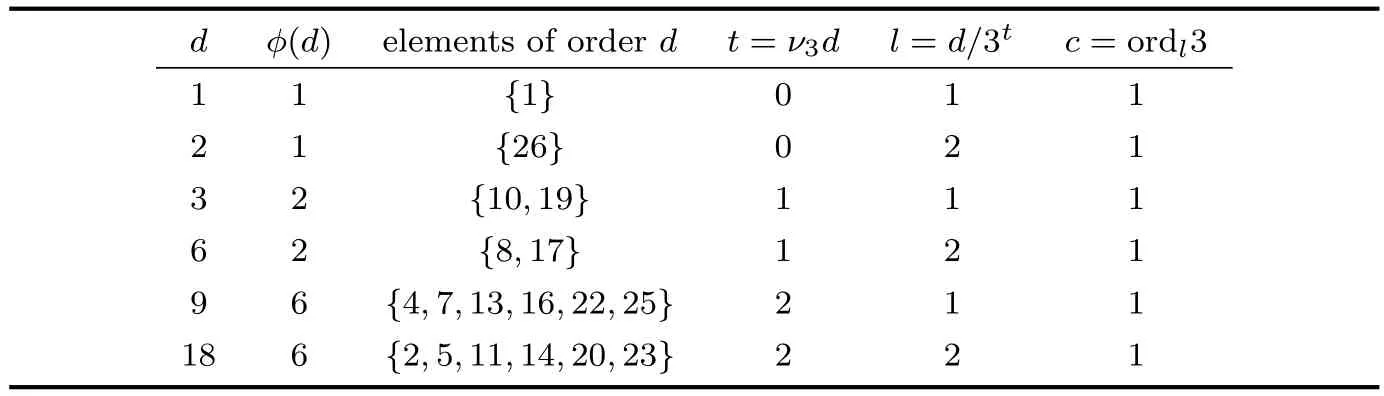
Table 2 The Structure of Gx→xpfor n=27,p=3.

>Figure2 The Topology of Gx→xpfor n=13,p=3.Figure 3 The Topology of Gx→xpfor n=27,p=3.

There are two special cases where we can give more details about the structure and properties of Gx→xp.The f i rst is when n=22m+1,a Fermat prime.

Remark 2.6Suppose n=22m+1 is a Fermat prime.If p is an odd prime,then (p,λ(n))=1.For any d|λ(n),it follows that(d,p)=1,which means that t=vp(d)=0,hence there only exist cycles in the digraph Gx→xpfor any Fermat prime n and odd prime p.

Example 2.3Table 3 and Figure 4 illustrate this construction when p=3,n=17.

Table 3The Structure of Gx→xpfor n=17,p=3.

Figure 4 The Topology of Gx→xpfor n=17=222+1,p=3.

The second case where we can give a more complete description is when n is a prime of the form n=pq?(p?1),where p and q are prime numbers.In this case,we call n a prime of p-type.

Theorem 2.7When n=pq?(p?1),a prime of p-type,the digraph Gx→xpconsists of cycles whose length divides q?1.Of feach element in these cycles there hang p?1 elements with tail length 1.

ProofSince(p,pq?1?1)=1 and n is an odd prime,it follows that λ(n)=n?1= p(pq?1?1)=pτ·ω,where τ=1 and ω=pq?1?1.Suppose d is any positive divisor of λ(n),then d must be of the form d=pf·j,where f∈{0,1},and j|pq?1?1.We have ordjp|q?1.Therefore,by Theorem 2.1,the cycle length for any element is given by ordjp for some j|pq?1?1,i.e,the cycle length for every element is a divisor of q?1.It follows that of f each element in these cycles there hang p?1 elements with tail length 1 by(2)of Corollary 2.5,since τ=1.

Figure 5 illustrates Theorem 2.7 in the case,where q=2,p=3,n=7.

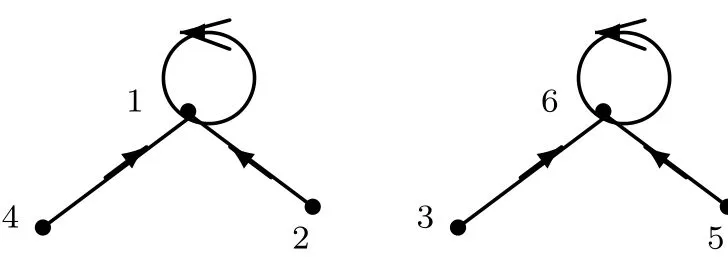
Figure 5 The Topology of Gx→xpfor n=7=32?2,p=3.

We now compute the average value of the tail and cycle lengths for a given number n. Denote tn(x)for the length of the tail in the orbit of x under this iteration,and cn(x)for the length of the cycle in the orbit of x.

Def i nition 2.1With respect to the iteration x→xp(mod n),we def i ne

?TC(n,p):=total number of cycles;

?T0(n,p):=total number of elements in all cycles,i.e.,the number of a∈Z?nwith t(a)=0;

?AC(n,p):=average length of a cycle;

?C(n,p):=average value of cn(a)over all a∈Z?n;

?T(n,p):=average value of tn(a)over all a∈Z?n.

Theorem 2.8Let λ(n)=pτ·ω,where(p,ω)=1.With respect to the iteration x→xp(mod n),we have

ProofParts(a)～(d)follow directly from Corollary 2.5.From Corollary 2.5,we know that for each positive divisor d of ω,Gx→xpcontains φ(d)/orddp cycles of length orddp,and that there exist ω elements in all these cycles and of feach element in these cycles there hang reversed complete α-ary trees of height τ?1 containing ατ?1 elements,where α=(p,λ(n)). Thus we can obtain

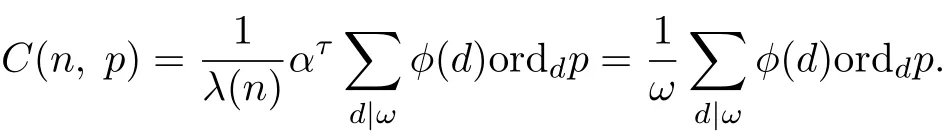
As for part(e),we have

Example 2.4We consider the digraph Gx→x3for n=27.It is clear that λ(27)=18=

32×2,τ=2,ω=2,α=3.By computation,we have

From Figure 3,we see that TC(27,3)=2,T0(27,3)=2,AC(27,3)=1,C(27,3)=1 and T(27,3)=14/9.

Similarly,we can compute out that C(7,3)=1,C(11,3)=,and C(13,3)=respectively, with respect to(λ,ω,τ,p)=(6,2,1,3),(10,10,0,3)and(12,4,1,3)respectively.

AcknowledgementThe authors are grateful to the referees for their careful reading of the original version of this paper,their detailed comments and suggestions that much improved the quality of this paper.

[1]SKOWRONEK-KAZIOW J.Some digraphs arising from number theory and remarks on the zero-divisor graph of the ring Zn[J].Information Processing Letters,2008,108:165-169.

[2]WILSON B.Power digraph modulo n[J].Fibonacci Q,1998,36:229-239.

[3]SOMER L,KRIZEK M.On a connection of number theory with graph theory[J].Czechoslovak Math J, 2004,54:465-485.

[4]SOMER L,KRIZEK M.Stucture of digraphs associated with quadratic congruences with composite moduli[J].Discrete Math,2006,306:2174-2185.

[5]SOMER L,KRIZEK M.The structure of digraphs associated with the congruences xk≡y(mod n)[J]. Czechoslovak Math J,2011,61:337-375.

[6]VASIGA T,SHALLIT J.On the iteration of certain quadratic maps over GF(p)[J].Discrete Math,2004, 277:219-240.

[7]CARMICHAEL R D.Note on a new number theory function[J].Bull Amer Math Soc,1910,16:232-238.

[8]KRIZEK M,LUCA F,SOMER L.17 Lectures on the Fermat Numbers:From Number Theory to Geometry[M].New York:Springer-Verlag,2001.

[9]IRELAND K,ROSEN M.A Classical Introduction to Modern Number Theory[M].New York:Springer-Verlag,1990.

tion:11A07,05C20

1002–0462(2014)04–0565–08

date:2013-03-03

Supported by the National Natural Science Foundation of China(11271208)

Biographies:JU Teng-xia(1972-),female,native of Yangzhou,Jiangsu,an associate professor of Nantong University,Ph.D.,engages in ring;WU Mei-yun(1971-),female,native of Nantong,Jiangsu,an associate professor of Nantong University,M.S.D.,engages in ring.

CLC number:O153.3Document code:A