歐拉恒等式與Amitsur-Levitzki定理

魏亞萍,曹明,馮怡君,游松發(fā)

(湖北大學(xué)數(shù)學(xué)與計算機科學(xué)學(xué)院,湖北 武漢 430062)

0 引言

令Γ是有多重邊的有限有向連通圖,其頂點集V(Γ)={1,…,k},邊集E(Γ)={e1,…,eN}.σ,τ是E(Γ)到V(Γ)的映射,并定義σ(es)=i,τ(es)=j,由此可知es為頂點i到頂點j的有向邊,對i∈V(Γ),令φ+(i)=|{es|σ(es)=i}|,φ-(i)=|{es|τ(es)=i}|,且γ(i)=max{φ+(i),φ-(i)}.若π∈Sym(N)(作用在{1,…,N}上的對稱群),且τ(eπ(i))=σ(eπ(i+1))(?i=1,…,N-1),則稱eπ(1)eπ(2)…eπ(N)是Γ的一條歐拉路,具有歐拉路的有向連通圖稱為歐拉圖.眾所周知,連通圖Γp,q有從p到q的歐拉路,當(dāng)且僅當(dāng)下列兩個條件之一成立:

a)p=q時,φ+(i)=φ-(i)(?i=1,…,k);

b)p≠q時,φ+(p)=φ-(p)+1,φ-(q)=φ(q)+1,且φ+(i)=φ-(i)(?i∈{1,…,k}(〗p,q}).

由定理0.1立即可以得到

推論0.1[1]令Γp,q是歐拉圖,且|V(Γp,q)|=k,|E(Γp,q)|=N,若N≥2kn,則fΓp,q(x1,…,xN)=0是域F上n×n矩陣環(huán)Mn(F)的多項式恒等式.

1 主要結(jié)果

則有

定理1.1若R是有1的F-代數(shù),f∈F〈X〉,則下列結(jié)論等價.

1)f=0是Mn(R)的多項式恒等式;

2)對所有1≤i,j≤n,φij(f)=0是R的多項式恒等式;

3)φ11(f)=0是R的多項式恒等式.

定理1.1的證明1)?2)及2)?3)是顯然的,只須證明3)?2).

因此,?i=1,…,n,φii(f)=0是R的多項式恒等式.

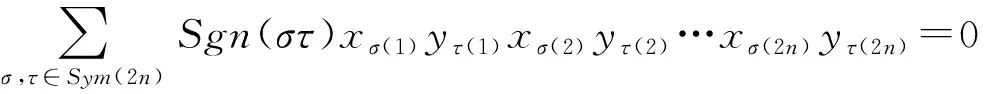
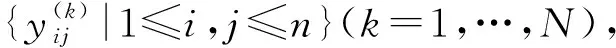
1)f=0是Mn(R)的多項式恒等式;

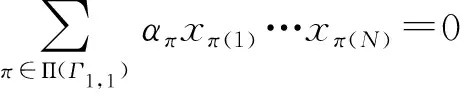
定理1.2的證明由f是多重線性時φij(f)的上述刻畫,直接應(yīng)用定理1.1,獲證.

[1] Szigeti J, Tuza Z, Revesz G. Eulerian polynomial identities on matrix rings[J]. J Algebra,1993,161:90-101.

[2] Rowen L H. Polynomial Identities in Ring Theory[M]. New York: Academic Press,1980.

[3] Chang Q. Some consequences of the standard polynomial[J]. Proc Amer Math Soc,1988,104:707-710.

[4] Giambruno A, Sehgal S K. On a polynomial identity forn×nmatrices[J]. J Algebra,1989,126:451-453.

[5] You Songfa, Zheng Yumei, Hu Donggang. Eulerian graph and polynomial identities on matrix rings[J]. Advances in Math,2003,32(4):425-428.

[6] You Songfa. The primitivity of extended centroid extension on prine GPI-rings[J]. Advances in Math,2000,29(4):331-336.

[7] You Songfa. The essential (one-sided) ideal of semiprime PI-rings[J]. Acta Math Sinca,2001,44(4):747-752.