Translocation of Polymer Through a Nanopore Studied by Langevin Dynamics: Effect of the Friction Coefficient*
FENG Jian (馮劍), SHANG Yazhuo (尚亞卓), ZHOU Lihui (周麗繪), LIU Honglai (劉洪來),**and HU Ying (胡英) Department of Applied Chemistry, Chuzhou University, Anhui 390, China State Key Laboratory of Chemical Engineering and Department of Chemistry, East China University of Science and Technology, Shanghai 0037, China
Translocation of Polymer Through a Nanopore Studied by Langevin Dynamics: Effect of the Friction Coefficient*
FENG Jian (馮劍)1, SHANG Yazhuo (尚亞卓)2, ZHOU Lihui (周麗繪)2, LIU Honglai (劉洪來)2,**and HU Ying (胡英)21Department of Applied Chemistry, Chuzhou University, Anhui 239012, China2State Key Laboratory of Chemical Engineering and Department of Chemistry, East China University of Science and Technology, Shanghai 200237, China
The driven polymer translocation through a nanopore with unbiased initial configuration has been studied by using Langevin dynamics (LD) simulations. It is found that the scaling relationship between translocation time and the polymer chain length is strongly affected by the friction coefficient in LD and the driving force. However, there is no scaling relationship between the translocation time and the friction coefficient. The translocation time is almost inversely proportional to the driving force, which is in agreement with those obtained in biased translocation. The scaling relationship between gyration radius (Rg) of subchain at the trans side with the subchain length (L) is Rg~L0.33that is in good agreement with the limiting value for molten globule state, while the curve of Rgof subchain at the cis side has two distinct stages. During translocation, the subchain at the cis side is being stretched gradually, and the structure of the subchain transforms from sphere-like to rod-like. When the effect of stretching reaches the tail end, the subchain is at the most stretched state. Finally the subchain will rapidly restore to coil structure. According to the results of force analysis, the retarding force at the trans side is more crucial during the practical translocation.
translocation, Langevin dynamics, friction coefficient, polymer, nanopore
1 INTRODUCTION
The transport of charged biomolecules such as DNA, RNA and proteins in organism is important for life processes. The translocation of these biomolecules through a nanopore on the biomembrane is one of the most crucial elementary processes, for example, DNA and RNA transfer across core pore complexes, proteins transport through biological membrane channels, and virus penetrates from a virus head into a host cell, etc[1]. There have been considerable progresses in nanopore technology for DNA sequencing [2], and peptides and protein structure probing [3]. Studies on translocation mechanism of biomolecules will not only help to understand the fundamental law of the life processes, but also benefit to potential applications in fast DNA sequencing, gene therapy, protein structure analysis, the control of drug delivery, and so on.
As early as the 1980s of the last century, the experiment on translocation of biomolecules through a nanopore has been reported [4]. Kasianowicz et al. [5]first gave a linear relationship between translocation time (τ) and DNA chain length (N), τ~N. They constructed bio-nanopores on the lipid bilayer membrane by using α-hemolysin, and the single-strand DNA(ss-DNA) is transferred across α-hemolysin (α-HL)under the electric field. The translocation time is defined as the duration of the first monomer of ss-DNA entering into the nanopore and the final monomer leaving the nanopore in a successive translocation process, which is observed by the current blockage when DNA is entering into the nanopore. Since then,α-HL is widely used as bio-material to construct nanopores in translocation experiments, and the studies concern with all aspects of properties in translocation, including the velocity of DNA in the nanopore[6], the relationship between the residence time of polymer and chain length [7, 8], a protein channel modified with aromatic binding sites to differentiate and quantify short peptides [9], using electrolyte solutions containing organic salts to slow down translocation [10], and so on.
The electric field, temperature, salinity and pH,etc. have important effect on the performance of protein pore. Li et al. [11, 12] showed that the solid-state nanopore could be used to study DNA translocation.Storm et al. [13, 14] reported the translocation of doublestrand DNA molecules through silicon oxide nanopores.The scaling relationship of translocation time with chain length is τ~N1.27, which is different from that obtained by Kasianowicz et al [5]. The experimental results have greatly promoted the theoretical [15-22]and computational [23-36] studies. For free translocation without electric field, it was found that the scaling relationship of translocation time and chain length is about τ~N2.5in both two-dimensional (2D) and three-dimensional (3D) systems [17, 25]. When solvent exists, the scaling exponent increases with increasing diameter of the nanopore [33]. When the translocation is driven by external electric field, several scaling relationship were obtained in 2D or 3D systems,including τ~N [15]; τ~N for short chains, τ~N1+νfor Rouse model and τ~N2νfor Zimm model for long chains (v is Flory energy parameter) [34]; τ~N1+νfor long chains and τ~N2νfor short chains in twodimensional system, but τ~N1.42in 3D system [29], as well as τ~N1.28and τ~N1.31with and without hydrodynamic interactions in 3D systems, respectively [36],and so on.
In translocation, the scaling relationship between translocation time and polymer chain length is related with the methods [37, 38] and model parameters [25, 38]applied in translocation study, especially for the driving force and the friction coefficient. This work will focus on the effect of the friction coefficient and the driving force in Langevin dynamics (LD) simulations on the configuration and the force of a monomer endured in translocation to clarify the mechanism of driven polymer translocation.
2 MODEL AND METHOD
In the case of translocation, a DNA molecule is described by a coarse-grained polymer and the solvent is treated as a continuous medium. The 3D simulation box is rectangular with dimensions Dσ×Dσ×2Dσ,referring to Fig. 1, and D varies in the simulations according to the polymer length. σ is a unit of length.The translocation is along the direction of z axis. A cylindrical nanopore is fixed at the center of the simulation box with a length l=5σ and a diameter d 3σ[27], which consists of a surface layer of Lennard-Jones (LJ) particles. The choice of the diameter will make the polymer pass through a nanopore without any folding. The length of a nanopore has a little influence on the polymer translocation [23, 24]. Thus,they are fixed to explore the effect of the friction coefficient and the driving force. In order to separate the simulation box to cis and trans chamber, two planes parallel to xy plane are located at the outer edges of the cylindrical pore. The planes are viewed as walls consisted of the LJ pseudo-particles, which means that when a monomer of the polymer molecule nears the wall, there is a wall particle with the same x and y coordinate colliding with it. The periodic boundary condition is only applied in x and y dimensions. The polymer length N varies from 40 to 200 with an interval 40 in the simulations. Half of the polymer is set to pass through the nanopore and the initial position of monomers in the polymer is randomly assigned. Applying this model to study the translocation of a polymer through a nanopore is not only to avoid specific method in simulations to increase the success ratio for biased translocation, which may slightly affect the translocation properties, but also to make the almost same configuration entropy before a translocation run.

Figure 1 A schematic representation of the translocation system (The pore length l=5σ and the diameter d=3σ)
The interactions between various kinds of particles are modeled as a series of cut and shifted Lennard-Jones (SLJ) potential with different cutoff distances.The LJ potential is

where ε is the energy parameter and σ is the size parameter. They are used as units of energy and length,respectively. The energy interaction parameters are fixed to 1ε for the LJ potential. The only varied value is the cutoff distance in LJ potential. The SLJ potential adopted in this work is [39]

where rcis the cutoff distance,is the LJ potential at the cutoff distance, andis the derivative of LJ potential with respect to the distance r at the cutoff distance. The cutoff distance between a monomer of polymer and a pseudo-particle in the wall,or between the monomers of DNA is rc=21/6σ, while rc2σ between a monomer of polymer and a particle of the nanopore.
The connective interaction between two bonded polymer monomer is modeled by a finite extension of a nonlinear elastic potential (FENE),

where the spring coefficient is k=7ε/σ2and the maximum extension R0is equal to 2σ. When a monomer of polymer enters into the nano tube, it will be affected by a driving force parallel to the tube axis.The driving force is

where f is the modulus of the driving force and the unit is ε/σ. The effect of the driving force on the translocation is explored by changing this value.
The stochastic Langevin equation for particle i is given by
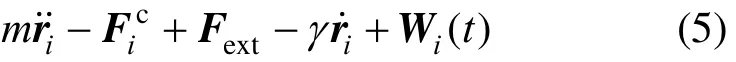
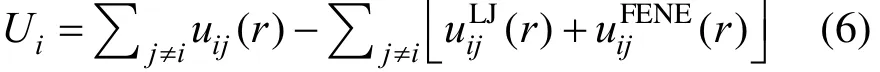
Random force Wi(t) in Eq.(5) satisfies the fluctuationdissipation relationship.
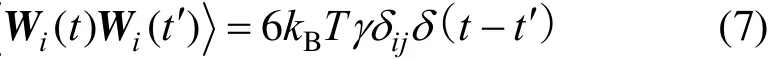
where γ is the friction coefficient with a unit of(mε/σ2)1/2. The value of the friction coefficient is varied from 1 to 4 in the simulations to explore the effect of it on the translocation process. If the friction coefficient is set to be zero, the NVT ensemble will become to NVE one. However, too small friction coefficient may cause failing in LD simulations without special treatment.
In this work, the time step Δt is set to 0.0025(mσ2/ε)1/2and the temperature is set to 1.2ε/kB. Because the initial position of the polymer is randomly assigned, the first 20000 time steps are equilibrium process to relax the initial configuration of polymer molecule before starting translocation movement.
3 RESULTS AND DISCUSSION
3.1 Translocation time
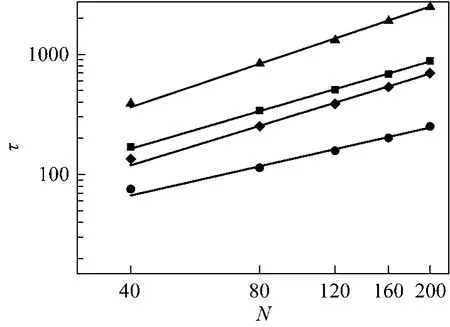
Figure 2 Translocation time τas a function of the chain length N■ γ=1, f=0.5; ▲ γ=4, f=0.5; ● γ=1, f=2; ◆ γ=4, f2
The scaling relationships between the translocation time and the polymer chain length at different driving forces and friction coefficients are an important subject in theoretical and computational studies.Fig. 2 shows the relationship between the translocation time τ and the polymer chain length N at different driving forces and friction coefficients. From the simulation data, when the driving force is set to f0.5,the scaling relationship is τ~N1.04±0.02and τ~N1.20±0.03at the friction coefficient γ=1 and γ=4, respectively.Similarly, the scaling relationship is τ~N0.81±0.05for γ 1 and τ~N1.09±0.04for γ 4 at the driving force f 2.The driving force and the friction coefficient strongly affect the scaling exponent, which has also been found in three-dimension (3D) system for biased translocation [40]. The scaling relationship means that the larger coefficient creates the longer translocation time at the same driving force, which is in agreement with that obtained in two-dimension system for biased translocation for short polymer [25]. The scaling exponents do not have obvious changes in fast translocation or slow translocation at the same friction coefficient with smaller force difference [40]. However, when the difference of the driving force becomes very large, increasing driving force will decrease the scaling exponent[40], which is in agreement with our results. The effect of the driving force on the exponents has also been obtained for the α-helix chain [41]. In LD simulation,the friction coefficient reflects the viscosity of solvent which is inherited in the LD simulation. The larger friction coefficient, the more viscous the solution is.The results show that the viscosity of the solution can strongly affect the translocation process of a polymer passing through a nanopore.
The driving force strongly affects the scaling relationship between the translocation time and the polymer chain length when all other parameters are fixed. For the same system, the larger driving force creates the smaller scaling exponent. So seeking to resolve the deference in experiments with protein nanopore [5] and solid nanopore [13, 14] is not important. The deference in experimental condition, membrane and nanopore material will result in subtle discrepancies, leading to the difficulty to compare simulation results simply with experimental data.
Figure 3 (a) shows the relationship between translocation time and the friction coefficient at different fixed driving force. The results show that the translocation time τ is linear with respect to the friction coefficient γ at the fixed driving forces at N=200. However, when the friction coefficient is too small, the LD simulations would cause a scaling collapse as shown in Fig. 3 (b). The result is in agreement with that obtained in Ref. [25] at N 100 and f=5. It is assumed that there might be a scaling relationship τ~γβbetween the translocation time τ and the friction coefficient γ.Fig. 4 shows the relationship between scaling exponent β and chain length N. No fixed exponent for different chain length is observed, i.e., the exponent is related to the chain length. From the figure, a longer chain length gives the larger exponent resulted from the decrease of driving force with longer chain. The result indicates that no scaling relationship exists between the translocation time and the friction coefficient. This also shows indirectly that the scaling exponent between the translocation time and the chain length is strongly affected by the friction coefficient. The relationship between the translocation time and the driving force has also been studied at different friction coefficients as shown in Fig. 5. For the friction coefficient set to γ=1, the scaling relationship is τ~f?0.97±0.01,and τ~f?0.96±0.01for γ=4, which is also in excellent agreement with the result τ~f?0.97±0.02for N=100 and γ=0.7 [25] and in 3D system for short chain [40].

Figure 3 Translocation time τ as a function of the friction coefficient γ at N 200 (a) and for smaller friction coefficients at f=2 (b)f: ■ 0.5; ● 0.2

Figure 4 The relationship between β and the chain length N f: ■ 0.5; ● 0.2
3.2 Residence time
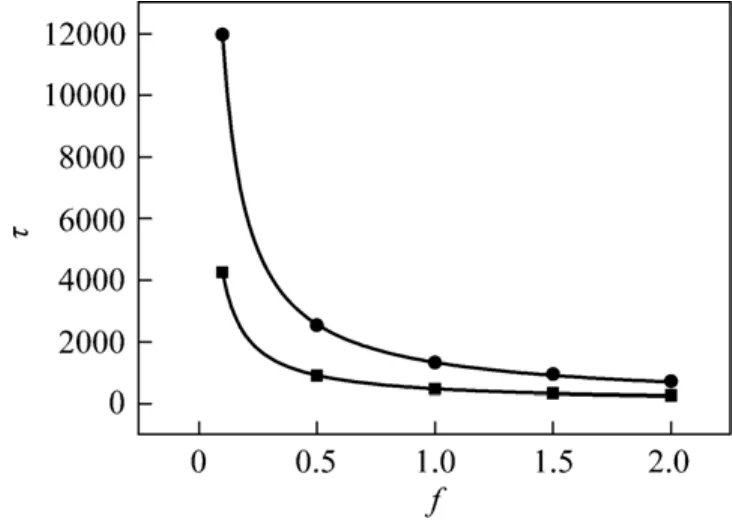
Figure 5 Translocation time as a function of the driving force at N 200 γ: ■ 1; ● 4
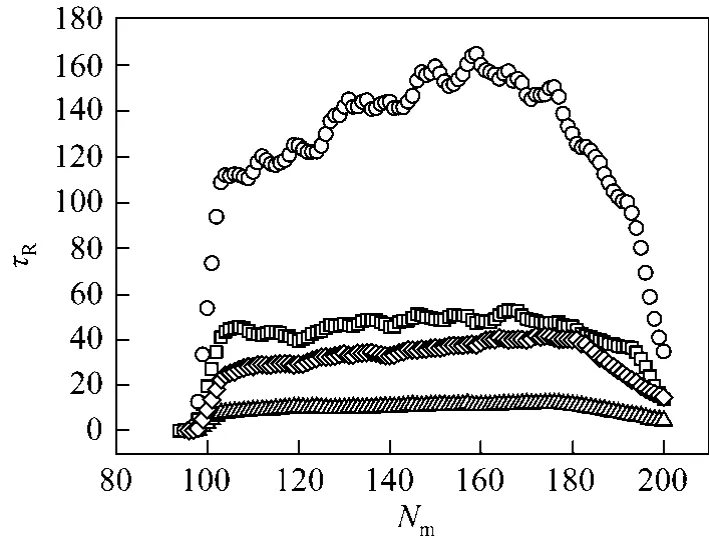
Figure 6 Residence times of a polymer at N=200□ γ 1, f 0.5; ○ γ 4, f 0.5; △ γ=1, f=2; ◇ γ 4, f 2
The mean monomer residence time (abbreviated as the residence time) is defined as the average duration of one monomer of a polymer entering into and leaving a nanopore. The residence time is also strongly affected by the friction coefficient and the driving force. Fig. 6 gives the relationship between residence times and different monomers in a polymer at different coefficient frictions and driving forces.The monomers of a polymer are assigned numbers to from the one at the trans side to that at the cis side. At the same driving force, the larger friction coefficient leads to the larger residence times. Although the curve of the residence time at γ 1 is flatter than that at γ 4 from the figure, in general, the curve of residence times has a maximal value. The residence time seemingly continues to decrease due to the longer subchain length at the trans side than at the cis side in this model, so the maximum value only occurs in the initial stage considering the effect of the configurational entropy. In fact, the non-equilibrium state of a polymer in translocation is responsible for these phenomena.The monomers transporting from cis side to trans side will disturb the configuration of the subchain in both side of the nanopore. However, the change in the configuration of both subchains, which grows at the trans side and shortens at the cis side, have no enough time to be relaxed, because the translocation process is too fast. So to those monomers in nanopore, the subchain packed at the trans side will create a retarding force and the subchain at the cis side will create a drag force.The direction of both forces is opposite to that of the driving force, which will be further illustrated in the later part. The co-activation of the retarding force, the drag force and the driving force etc. give the maximal value in the plot. The friction coefficient strongly affects the relaxation time of the subchain. An increase in the friction coefficient will decrease the relaxation time of the subchain, which will also affect the retarding force and the drag force, and then affect the residence time.
3.3 Configuration
The gyration radius of subchain in both cis side and trans side could be used to explore the configuration of the polymer in the translocation process. Fig. 7 shows the gyration radius of subchain at the cis side at two kinds of friction coefficients and driving forces at N=200. If the driving force is fixed, the gyration radius will be a little larger at smaller friction coefficient.The reason is that the larger friction coefficient will create larger relaxation time, so the perturbation in subchain length cannot be relaxed in time which will make the subchain present a contracted structure. It is worth noting that, from Fig. 7, there are two obvious stages in the plot of the gyration radius, which also appear in biased translocation [42]. In the first stage,the gyration radius decreases slowly with chain length shortening, then the gyration radius decreases rapidly in the final stage. It means that the subchain at the cis side near a nanopore is continuously stretched. As shown in Fig. 8, a snapshot is presented for the chain length N=200 at γ=4 and f0.5. The result has also been given by analysis of the gyration radius [42].

Figure 7 Gyration radius of subchain at the cis side at different external force and friction coefficient at N 200□ γ=1, f=0.5; ○ γ=4, f=0.5; △ γ=1, f=2; ◇ γ=4, f2
The effect of the friction coefficient on the configuration of subchain at the trans side is similar to that at the cis side. Fig. 9 shows the relationship between the gyration radius of subchain at the trans side for chain length N 200 at different friction coefficients and driving forces. The subchain will be also more stretched at the small friction coefficient than at the large one. Unlike at the cis side, no clear two-stage phenomenon exists for the configuration at the trans side. The gyration radius of subchain has a good scaling relationship with the subchain length L at the trans side. Without considering the difference resulted from the friction coefficient and the driving force, the scaling relationship between the gyration radius and the subchain length L is Rg~L0.33±0.01at the trans side. The scaling exponent is less than 0.6 of self-avoiding chain obtained by Flory-Huggins theory. The scaling exponent at the trans side is equal to the limiting value v 1/3 for molten globule states [43].

Figure 8 Snapshot of a polymer passed through a nanopore from cis side (left) to trans side (right) at γ=4 and f 0.5 for N 200
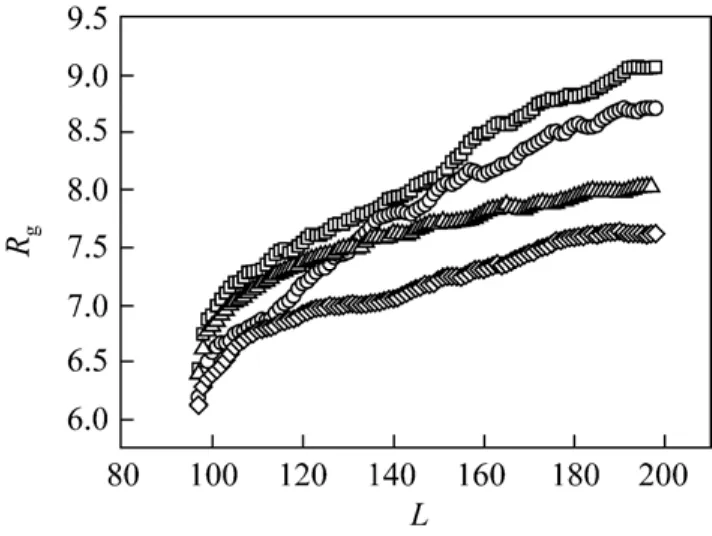
Figure 9 Gyration radius of subchain at the trans side at different external force and friction coefficient at N 200□ γ 1, f0.5; ○ γ 4, f0.5; △ γ=1, f=2; ◇ γ 4, f2

Figure 10 Changes of aspheric coefficient of the whole chain and subchains in both sides in translocation process at γ=1 and f=2 for N=200□ whole; ○ cis; △ trans
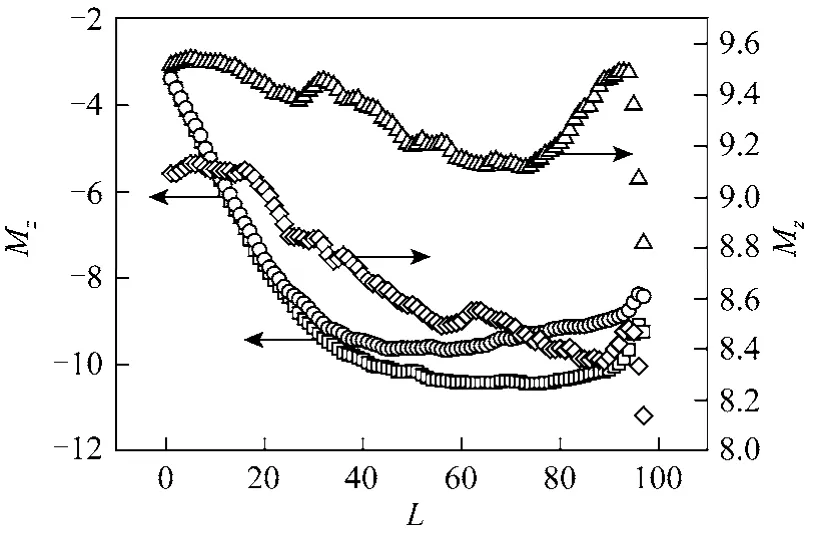
Figure 11 Values of center of gravity of subchain in z coordinate in both side with two kinds of friction coefficients at f=2, N=200□ γ=1, cis; ○ γ=4, cis; △ γ=1, trans; ◇ γ=4, trans
To give a clear picture of polymer translocation,Figs. 10 and 11 show the changes in aspheric coefficient and center of gravity of a polymer, respectively.The aspheric coefficient is evaluated from three eigenvalues obtained by gyration tensor of a chain [44],which is more suitable for showing the configuration change than the gyration radius. A value of 1 of the aspheric coefficient indicates that the chain shape is a straight line, and the value 0 shows a perfect sphere.The abscissa in both Figs. 10 and 11 is the subchain length at the cis side. The aspheric coefficient of subchain at the cis side mainly falls into three stages without considering the three tail end monomers,where the aspheric coefficient A is changed rapidly from 0.6 to 1. The aspheric coefficient first increases slowly, then increases rapidly, and finally decreases. It means that the configuration of subchain at the cis side is forming a sphere-like structure (coil state) at the initial stage, then the shape trends to rod-like structure slowly and after that rapidly with the translocation continuing. However, at the third stage (about the last twenty monomers), the subchain becomes more sphere-like again. The change of aspheric coefficient at the trans side is simple, which decreases slowly as a whole. The aspheric coefficient of the whole chain first decreases and finally increases. The changes of aspheric coefficient at γ=1, γ 4, and f=0.5, f=2 have the similar tendency.
From Fig. 11, although the subchain length decreases in translocation, the distance of center of gravity of subchain at the cis side to the nanopore almost maintains unchanged, even increase a little, before almost half of monomers pass through a nanopore.Then the distance decreases fast after about half of monomers have passed through the nanopore. The changes in aspheric factor and the center of gravity of subchain at the cis side indicate that the subchain near a nanopore is stretched continuously with the end monomers unaffected. At the initial stage, the numbers being stretched is less than the half numbers of the subchain at the cis side, leading to small changes in statistical quantities such as gyration radius, aspheric coefficient and center of gravitation etc. When the stretched monomers are superior in numbers, the statistical quantities change rapidly. After the effect of stretched monomers reaches to the tail end of the subchain at the cis side, where the subchain tends to the most stretched structure, and then the effect of stretched monomers diminish contrarily, and the subchain is restored to coil state gradually. Of course, due to fast translocation in this stage, the retarding effect of subchain at the trans side will also become much stronger. The distance of subchain at the trans side from the nanopore begins to increase after translocation, which can be explained by the deviation of the equilibrium state of the subchain, and then the center of gravity of the subchain moving away from the nanopore. The larger the driving force is, the larger the perturbation is. If the driving force is large enough such as f2, the subchain will approach the nanopore again in the intermediate stage, which can be found in Fig. 11. However, from our simulations, when the driving force is small enough to such as f0.5, the center of gravity of subchain at the trans side always move far from the nanopore, which is resulted from the fact that the residence time is less than the relaxation time.
3.4 Force analysis
In translocation, a monomer in a nanopore is exerted on by many forces, including the driving force,the retarding force, the drag force, and the interaction resulted from the nanopore, as well as the friction force and viscous force come from LD thermostat, etc.The resultant force determines the motion of a monomer in a nanopore. Fig. 12 (a) shows the net force of a monomer being in the nanopore when the driving force is at f2 and N 200, where the forces of some initial monomers are omitted for clear illustration due to the too large values which will interfere the exhibition of other monomers as shown in the inset at the corner. From Fig. 12 (b), the largest fluctuation occurs at the initial stage of the translocation process and a peak occurs for the net force. At the starting stage, the retarding force resulted from subchain at the trans side is very small because the effect of subchain packing in the trans side is small, which make the net force become very large. After several monomers pass through the nanopore, the increasing retarding force leads to the net force diminish rapidly. For most of monomers,the net force is basically stable. Due to the subchain shortening at the cis side during the translocation, the drag force will diminish. From the fact that the net force decreases quickly, the retarding force at the trans side is more crucial than the drag force at the cis side during the process. At the final stage, when about the last twenty monomers pass through the nanopore,the net force is more negative. From Fig. 10, the subchain at the cis side of about the last twenty monomers, the stretching subchain will restore a coil state gradually, which also reflect that it is more difficult for the tail to travel through the nanopore because it is retarded by the former part of the chain that has just left the pore. From Fig. 12 (a), even if the driving force is strong, the net forces of some monomers are less than zero. The average net force for all monomers in translocation is larger than zero, which are F=0.113 at γ=1 and F=0.142 at γ=4. When the driving force is at f=0.5, the average net forces of monomers are 0.123 at γ=1 and 0.136 at γ 4, respectively. Although the average net force is greater than zero, quantitatively, it is not decisive for the translocation, as shown in the figure, it is not expected that the average net force is higher at γ=4 than that at γ=1. So the translocation time is not determined by the magnitude of the net force of monomers in a nanopore. The other factors must be considered, such as the starting monomer velocity of translocation and the velocity of a monomer in both side, etc.
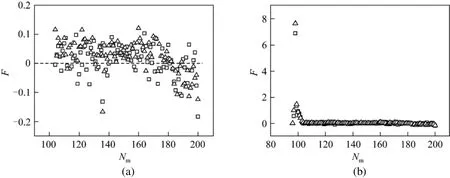
Figure 12 Net force subjected to a monomer in a nanopore at f 2 and N 200, where the dash line is for F=0 (a) and for the whole monomers in translocation (b)□ γ=1; △ γ=4
4 CONCLUSIONS
The driven polymer translocation through a nanopore with an unbiased initial configuration has been studied by LD simulations. Although the model is different, the effect of the friction coefficients in LD and the driving force is in good agreement with that obtained by biased translocation. For coarse-grained system without solvent, the friction coefficient is related to the viscosity of the solvent, and the larger friction coefficient indicates the more viscous solvent.At a fixed driving force, increasing the friction coefficient will increase the translocation time and the scaling exponent between the translocation time and the polymer chain length. It is worthy noting that the driving force also strongly affects the scaling relationship between translocation time and the chain length,which will decrease when increasing the driving force.The translocation time is in directly proportional to the friction coefficient and almost in inversely proportional to the driving force at fixed chain length. However, no scaling relationship is observed between translocation time and the friction coefficient. The residence time of monomers increases with increasing friction coefficient. The cooperation of a retarding force of subchain at the trans side and a drag force of subchain at the cis side as well as the driving force produces a maximal value in the residence time curve.The configuration of subchain is very different at the trans side from that at the cis side, and the subchain at the trans side is more contract than that at the cis side.The larger coefficient makes the subchain more contracted. The gyration radius of subchain at the trans side has a scaling relationship with the subchain length, and the relationship is Rg~L0.33that is comparable to the limiting value for molten globule state.However, the gyration radius of subchain at the cis side has two stages. Combined with aspheric coefficients and center of gravity of subchains in both sides,the configuration change in translocation can be obtained. During translocation, the subchain at the cis side is being stretched gradually, and the structure of the subchain will transform from sphere-like to rod-like. When the effect of stretching reaches the tail end, the subchain is the most stretched. Finally, the subchain will restore to a coil structure rapidly. The translocation time is not determined by the magnitude of the net force of monomers in a nanopore. The direction of interaction resulted from subchain in both sides is opposite to that of the driving force for most monomers. The retarding force at the trans side is more crucial than the drag force at the cis side during the practical translocation.
NOMENCLATURE
Fextdriving force
f modulus of the driving force
k spring coefficient
kBBoltamann factor
L subchain length
m mass of a particle
N polymer chain length
Nmnumber of a monomer
Rggyration radius
rccutoff distance
T thermodynamics temperature
t time
uijpotential between particles i and j
α, β scaling coefficient
γ friction coefficient
ε unit of the energy
σ unit of length
τ translocation time
1 Muthukumar, M., “Mechanism of DNA transport through pores”,Annu. Rev. Biophys. Biomol. Struct., 36, 435-450 (2007).
2 Branton, D., Deamer, D., Marziali, A., Bayley, H., Benner, S.A.,Butler, T., Ventra, M.D., “The potential and challenges of nanopore sequencing”, Nat. Biotech., 26 (10), 1146-1153 (2008).
3 Movileanu, L., “Interrogating single proteins through nanopores:challenges and opportunities”, Trends in Biotechnology, 27 (6), 333-341(2009).
4 Wickner, W.T., Lodish, H.F., “Multiple mechanisms of protein insertion into and across membranes”, Science, 230, 400-407 (1985).
5 Kasianowicz, J.J., Brandin, E., Branton, D., Deaner, D.W., “Characterization of individual polynucleotide molecules using a membrane channel”, Proc. Natl. Acad. Sci. U.S.A., 93, 13770-13733 (1996).
6 Meller, A., Nivon, L., Branton, D., “Voltage-driven DNA translocations through a nanopore”, Phys. Rev. Lett., 86 (15), 3435-3438 (2001).
7 Robertson, J.W.F., Rodrigues, C.G., Standford, V.M., Rubinson, K.A.,Krasilnikov, O.V., Kasianowicz, J.J., “Single-molecule mass spectrometry in solution using a solitary nanopore”, Proc. Natl. Acad. Sci.U.S.A., 104, 8207-8211 (2007).
8 Krasilnikov, O.V., Rodrigues, C.G., Bezrukov, S.M., “Single polymer molecules in a protein nanopore in the limit of a strong polymer-pore attraction”, Phys. Rev. Lett., 97, 018301 (2006).
9 Zhao, Q.T., Jayawardhana, D.A., Wang, D.Q., Guan, X.Y., “Study of peptide transport through engineered protein channels”, J. Phys.Chem. B, 113 (11), 3572-3578 (2009).
10 de Zoysa, R.S.S., Jayawardhana, D.A., Zhao, Q., Wang, D., Armstrong, D.W., Guan, X., “Slowing DNA translocation through nanopores using a solution containing organic salts”, J. Phys. Chem.B, 113, 13332-13336 (2009).
11 Li, J.L., Stein, D., McMullan, C., Branton, D., Aziz, M.J., Golovchenko,J.A., “Ion-beam sculpting at nanometre length scales”, Nature, 412,166-169 (2001).
12 Li, J.L., Gershow, M., Stein, D., Brandin, E., Golovchenko, J.A.,“DNA molecules and configurations in a solid-state nanopore microscope”, Natural Material, 2, 611-615 (2003).
13 Storm, A.J., Chen, J.H., Zandbergen, H.W., Dekker, C., “Translocation of double-strand DNA through a silicon oxide nanopore”, Phys.Rev. E, 71, 051903 (2005).
14 Storm, A.J., Storm, C., Chen, J., Zandbergen, H., Joanny, J.F., Dekker, C., “Fast DNA translocation through a solid-state nanopore”,Nano Lett., 5 (7), 1193-1197 (2005).
15 Muthukumar, M., “Polymer translocation through a hole”, J. Chem.Phys., 111, 10371-10374 (1999).
16 Ghosal, S., “Electrophoresis of a polyelectrolyte through a nanopore”, Phys. Rev. E, 74, 041901 (2006).
17 Dubbeldam, J.L.A., Milchev, A., Rostiashvili, V.G., Vilgis, T.A.,“Polymer translocation through a nanopore: A showcase of anomalous diffusion”, Phys. Rev. E, 76, 010801 (2007).
18 Wong, C.T.A., Muthukumar, M., “Polymer capture by electro-osmotic flow of oppositely charged nanopores”, J. Chem. Phys., 126, 164903(2007).
19 Gopinathan, A., Kim, Y.W., “Polymer translocation in crowded environments”, Phys. Rev. Lett., 99, 228106 (2007).
20 Lagerqvist, J., Zwolak, M., Ventra, M.D., “Influence of the environment and probes on rapid DNA sequencing via transverse electronic transport”, Biophys. J., 93 (7), 2384-2390 (2007).
21 Tai, C., Wong, C., Muthukumara, M., “Polymer translocation through a cylindrical channel”, J. Chem. Phys., 128, 154903 (2008).
22 ten Bosch, A., Cheyssac, P., “Translocation of a stiff polymer in a microchannel”, Phys. Rev. E, 79, 011903 (2009).
23 Luo, K.F., Ala-Nissila, T., Ying, S.C., “Polymer translocation through a nanopore: A two-dimensional Monte Carlo study”, J.Chem. Phys., 124, 034714 (2006).
24 Luo, K.F., Huopaniemi, I., Ala-Nissila, T., Ying, S.C., “Polymer translocation through a nanopore under an applied external field”, J.Chem. Phys., 124, 114704 (2006).
25 Huopaniemi, I., Luo, K.F., Ala-Nissila, T., Ying, S.C., “Langevin dynamics simulations of polymer translocation through nanopores”,J. Chem. Phys., 125, 124901 (2006).
26 Forrey, C., Muthukumara, M., “Langevin dynamics simulations of ds-DNA translocation through synthetic nanopores”, J. Chem. Phys.,127, 015102 (2007).
27 Luo, K.F., Ala-Nissila, T., Ying, S.C., Bhattacharya, A., “Influence of polymer-pore interactions on translocation”, Phys. Rev. Lett., 99,148102 (2007).
28 Luo, K.F., Ala-Nissila, T., Ying, S.C., Bhattacharya, A., “Heteropolymer translocation through nanopores”, J. Chem. Phys., 126, 145101(2007).
29 Luo, K.F., Ollila, S.T.T., Huopaniemi, I., Ala-Nissila, T., Pomorski,P., Karttunen, M., Ying, S.C., Bhattacharya, A., “Dynamical scaling exponents for polymer translocation through a nanopore”, Phys. Rev.E, 78, 050901 (2008).
30 Luo, K.F., Ala-Nissila, T., Ying, S.C., Bhattacharya, A., “Sequence dependence of DNA translocation through a nanopore”, Phys. Rev.Lett., 100, 058101 (2008).
31 Luo, K.F., Ala-Nissila, T., Ying, S.C., Bhattacharya, A., “Dynamics of DNA translocation through an attractive nanopore”, Phys. Rev. E,78, 061911 (2008).
32 Luo, K.F., Ala-Nissila, T., Ying, S.C., Bhattacharya, A., “Translocation dynamics with attractive nanopore-polymer interactions”, Phys.Rev. E, 78, 061918 (2008).
33 Gauthier, M.G., Slater, G.W., “Molecular dynamics simulation of a polymer chain translocating through a nanoscopic pore-hydrodynamic interactions versus pore radius”, Eur. Phys. J. E, 25, 17-23 (2008).
34 Gauthier, M.G.., Slater, G.W., “A Monte Carlo algorithm to study polymer translocation through nanopores. II. scaling laws”, J. Chem.Phys., 128, 205103 (2008).
35 Gauthier, M.G., Slater, G.W., “Sequence effects on the forced translocation of heteropolymers through a small channel”, J. Chem. Phys.,128, 175103 (2008).
36 Izmitli, A., Schwartz, D.C., Graham, M.D., de Pablo, J.J., “The effect of hydrodynamic interactions on the dynamics of DNA translocation through pores”, J. Chem. Phys., 128, 085102 (2008).
37 Lehtola, V.V., Linna, R.P., Kaski, K., “Critical evaluation of the computational methods used in the forced polymer translocation”,Phys. Rev. E, 78, 061803 (2008).
38 Feng, J., Ge, X. T., Shang, Y.Z., Zhou, L.H., Liu, H.L., Hu, Y.,“Translocation of polymer through a nanopore studied by dissipative particle dynamics”, Fluid Phase Equilibrium, 302, 26-31 (2011).
39 Leach, A.R., Molecular Modelling: Principles and Applications, 2nd edition, Pearson Education, England, 331-334 (2001).
40 Luo, K.F., Ala-Nissila, T., Ying, S.C., Metzler, R., “Driven polymer translocation through nanopores: Slow-vs.-fast dynamics”, EPL, 88,68006 (2009).
41 Yang, Z., Li, S., Zhang, L., Ur Rehman, A., Liang, H., “Translocation of α-helix chains through a nanopore”, J. Chem. Phys., 133 (22),154903 (2010).
42 Bhattacharya, A., Morrison, W.H., Luo, K.F., Ala-Nissila, T., Ying, S.C.,Milchev, A., Binder, K., “Scaling exponents of forced polymer translocation through a nanopore”, Eur. Phys. J. E, 29, 423-429 (2009).
43 Kapahnke, F., Schmidt, U., Heermann, D. W., Weiss, M., “Polymer translocation through a nanopore: The effect of solvent conditions”,J. Chem. Phys., 132, 164904 (2010).
44 Feng, J., Liu, H.L., Hu, Y., “Molecular dynamics simulations of polyampholytes inside a slit”, Mol. Simul., 31 (10), 731-738 (2005).
2011-03-19, accepted 2011-06-03.
* Supported by the National Natural Science Foundation of China (20736002, 20706013), the Open Project of the State Key Laboratory of Chemical Engineering ECUST (SKL-ChE-09C02) and the Natural Science Fund of the Education Department of Anhui Province (KJ2011B116).
** To whom correspondence should be addressed. E-mail: hlliu@ecust.edu.cn
 Chinese Journal of Chemical Engineering2012年2期
Chinese Journal of Chemical Engineering2012年2期
- Chinese Journal of Chemical Engineering的其它文章
- Optimization for Production of Intracellular Polysaccharide from Cordyceps ophioglossoides L2 in Submerged Culture and Its Antioxidant Activities in vitro*
- A Pilot-scale Demonstration of Reverse Osmosis Unit for Treatment of Coal-bed Methane Co-produced Water and Its Modeling*
- ECT Image Analysis Methods for Shear Zone Measurements during Silo Discharging Process*
- Temperature-triggered Protein Adsorption and Desorption on Temperature-responsive PNIPAAm-grafted-silica: Molecular Dynamics Simulation and Experimental Validation*
- Adsorptive Thermodynamic Properties and Kinetics of trans-1,2-Cyclohexandiol onto AB-8 Resin
- Tracking Submicron Particles in Microchannel Flow by Microscopic Holography*
