基于拓展Tullock 模型的開發(fā)商尋租博弈均衡策略

劉天虎 ,黃武軍 ,許維勝 ,吳啟迪,

(1.同濟(jì)大學(xué) 電子與信息工程學(xué)院, 上海200092;2.同濟(jì)大學(xué)經(jīng)濟(jì)與管理學(xué)院, 上海200092)

早在1980 年Tullock[1]就提出了尋租博弈的概念, Tullock 分析了尋租成本, 發(fā)現(xiàn)企業(yè)壟斷地位的獲取是有成本的, 且尋租中的企業(yè)壟斷會(huì)通過(guò)競(jìng)爭(zhēng)實(shí)現(xiàn)均衡, 均衡的結(jié)果使尋租成本與經(jīng)濟(jì)租的量值相等.Tullock 進(jìn)一步揭示了政府在對(duì)經(jīng)濟(jì)主體實(shí)施行政干預(yù)的過(guò)程中會(huì)造成資源的緊張, 誘發(fā)尋租行為,導(dǎo)致社會(huì)資源的浪費(fèi).Perez-Castrillo 等[2]證明了Tullock 尋租博弈模型具有唯一的純策略Nash均衡.Bruce[3]分析了尋租博弈者的風(fēng)險(xiǎn)中性行為模式,提出了Stackelberg 博弈模型, 實(shí)現(xiàn)了在不完全信息下的子博弈均衡.次年, Bruce[4]研究了重復(fù)尋租博弈中的合作行為, 利用重復(fù)博弈的特性來(lái)維持尋租的合作性, 并將Nash 談判均衡應(yīng)用于對(duì)稱和不對(duì)稱的尋租環(huán)境中.Skaperdas 等[5]研究了兩位具有風(fēng)險(xiǎn)厭惡特性的博弈方的純策略N ash 均衡的存在條件.Szidarovszky 等[6]證明了在生產(chǎn)函數(shù)嚴(yán)格遞增且呈凸性的情況下,尋租博弈的非對(duì)稱純策略Nash均衡的唯一存在性.在此博弈中, 所有參與者都假定為風(fēng)險(xiǎn)中性的.William[7]建立了N位對(duì)稱競(jìng)爭(zhēng)對(duì)手的尋租博弈模型,每位博弈方都對(duì)尋租有不同賦值,且各自能力不同, 其中一位基于Tullock 概率能獲勝,由此得到純策略Nash 均衡.Cornes 等[8]允許風(fēng)險(xiǎn)厭惡的博弈方參與Szidarovszdy 尋租博弈模型,證明了純策略Nash 均衡的存在.David 等[9]給出了對(duì)稱尋租博弈的純策略Nash 均衡, 在競(jìng)爭(zhēng)成功函數(shù)同質(zhì)的條件下均衡策略具有簡(jiǎn)單模式, 并給出了均衡存在的充分條件.Matros[10]對(duì)T ullock 尋租博弈模型進(jìn)行了擴(kuò)展,證明了隨著租金費(fèi)用的增加,尋租人成功的機(jī)會(huì)將減少, 更多尋租人的參與將導(dǎo)致租金發(fā)生變動(dòng), 得到了尋租博弈的純策略均衡.Riechmann[11]建立了局中人相對(duì)支付最大化的Tullock 尋租博弈數(shù)學(xué)模型, 研究表明, 局中人傾向于為尋租過(guò)程過(guò)度投入, 租金的耗費(fèi)與局中人數(shù)量無(wú)關(guān).Yamazaki[12-13]假定博弈方受到尋租活動(dòng)的收益及預(yù)算約束, 其均衡受到一定的限制,基于對(duì)稱尋租博弈的特點(diǎn), 證明了純策略Nash 均衡的存在.Matros[14]分析了存在補(bǔ)償條件下的Tullock 尋租博弈模型,研究表明獲得補(bǔ)償?shù)木种腥藢⒆畲蠡呺H支付,而失去補(bǔ)償?shù)木种腥藢⒆钚』呺H支付, 并證明了均衡策略的唯一性.Schoonbeek[15]分析了存在潛在進(jìn)入者的兩階段Tullock 尋租博弈模型, 第一階段通過(guò)賄賂來(lái)規(guī)避競(jìng)爭(zhēng),第二階段則實(shí)施尋租競(jìng)爭(zhēng),得到了存在潛在進(jìn)入者的均衡策略.

而房地產(chǎn)開發(fā)商對(duì)土地資源的尋租實(shí)際上也是一種不完全信息博弈, 博弈各方的信息是不對(duì)稱的[16-17] .由于尋租競(jìng)爭(zhēng)的存在, 開發(fā)商有機(jī)會(huì)獲得尋租的成功,也可能會(huì)失敗, 可見開發(fā)商面對(duì)的是不確定性條件下的選擇, 各位開發(fā)商的風(fēng)險(xiǎn)態(tài)度會(huì)影響他的行為.本文將對(duì)T ullock 尋租博弈模型進(jìn)行擴(kuò)展,研究開發(fā)商土地尋租博弈的均衡解.

1 經(jīng)典Tullock 模型

Tullock[1]提出了經(jīng)典的尋租博弈理論, 基于Tullock 的尋租博弈模型,若令N≡{1 ,2,…,n}為N位博弈局中人, 局中人i為獲取勝利而付出的努力可用x i表示,X=(x1,x2,…,xn), 其中局中人i獲取勝利的概率可表示為πi(X), 令(π1,π2,…, πn)為競(jìng)爭(zhēng)成功函數(shù), 對(duì)于尋租博弈的成功而言, 所有局中人都有一個(gè)普遍一致的估值VAL,在局中人都是風(fēng)險(xiǎn)中性的前提下,局中人i的期望效用為

Tullock 的競(jìng)爭(zhēng)函數(shù)可表示為[18]

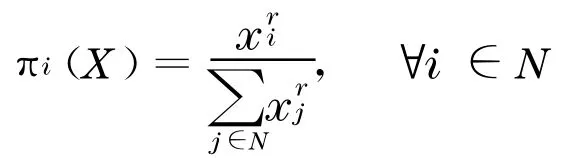
其中,r＞0 .

Skaperdas[19]通過(guò)5 條公理對(duì)Tullock 競(jìng)爭(zhēng)函數(shù)進(jìn)行了完整的描述:

公理1 (可能性)對(duì)于 ?i∈N,?X,有如果x i＞0 ,則有πi(X)＞0 .

公理2 (單調(diào)性)對(duì)于?i∈N,?j≠i,πi(X)在xi域是遞增的,在x j域是遞減的.

公理4 (獨(dú)立性)對(duì)于?S?N,?i∈S,πSi(X)與集合S之外的博弈參與人是相互獨(dú)立的.

公理5 (同質(zhì)性)對(duì)于?t＞0,?X,?i∈N,有πi(tX)=πi(X).

公理1 和公理2 表明Tullock 競(jìng)爭(zhēng)成功函數(shù)具有概率函數(shù)的特性, 局中人增加努力會(huì)使其成功的可能性增大,從而使其他局中人的成功機(jī)會(huì)減少.公理3 表明任何兩位局中人在相同努力下的成功可能性是相同的.公理4 表明如果某位局中人a1 未能獲勝,則a1對(duì)于其他局中人的獲勝可能性不帶來(lái)影響.公理5 表明任意兩位局中人的努力具有同質(zhì)性.

2 尋租博弈分析

2 .1 尋租博弈模型的改進(jìn)

同樣,可將尋租的期望效用推廣到N位開發(fā)商競(jìng)爭(zhēng)的模式,則eTi可由n×n的矩陣表示,用來(lái)表示開發(fā)商的效用支付:

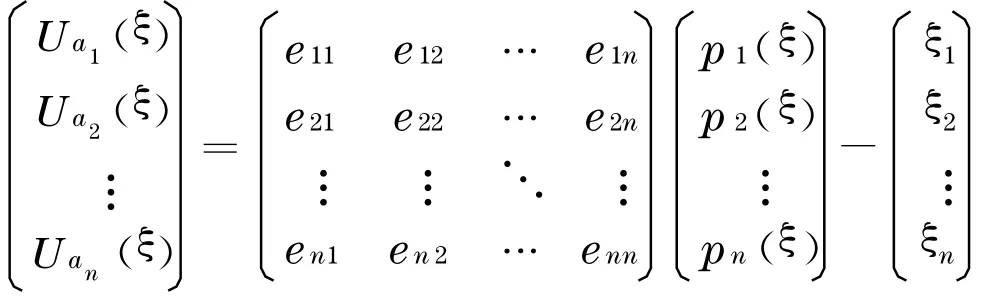
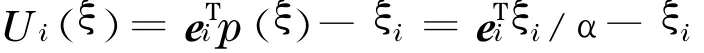
為了得到開發(fā)商a1的最優(yōu)支付條件, 需對(duì)U a1(ξ)求偏導(dǎo):

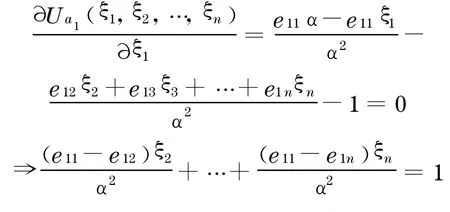
用同樣的方法, 可以得到每一位開發(fā)商的最優(yōu)支付條件如下:

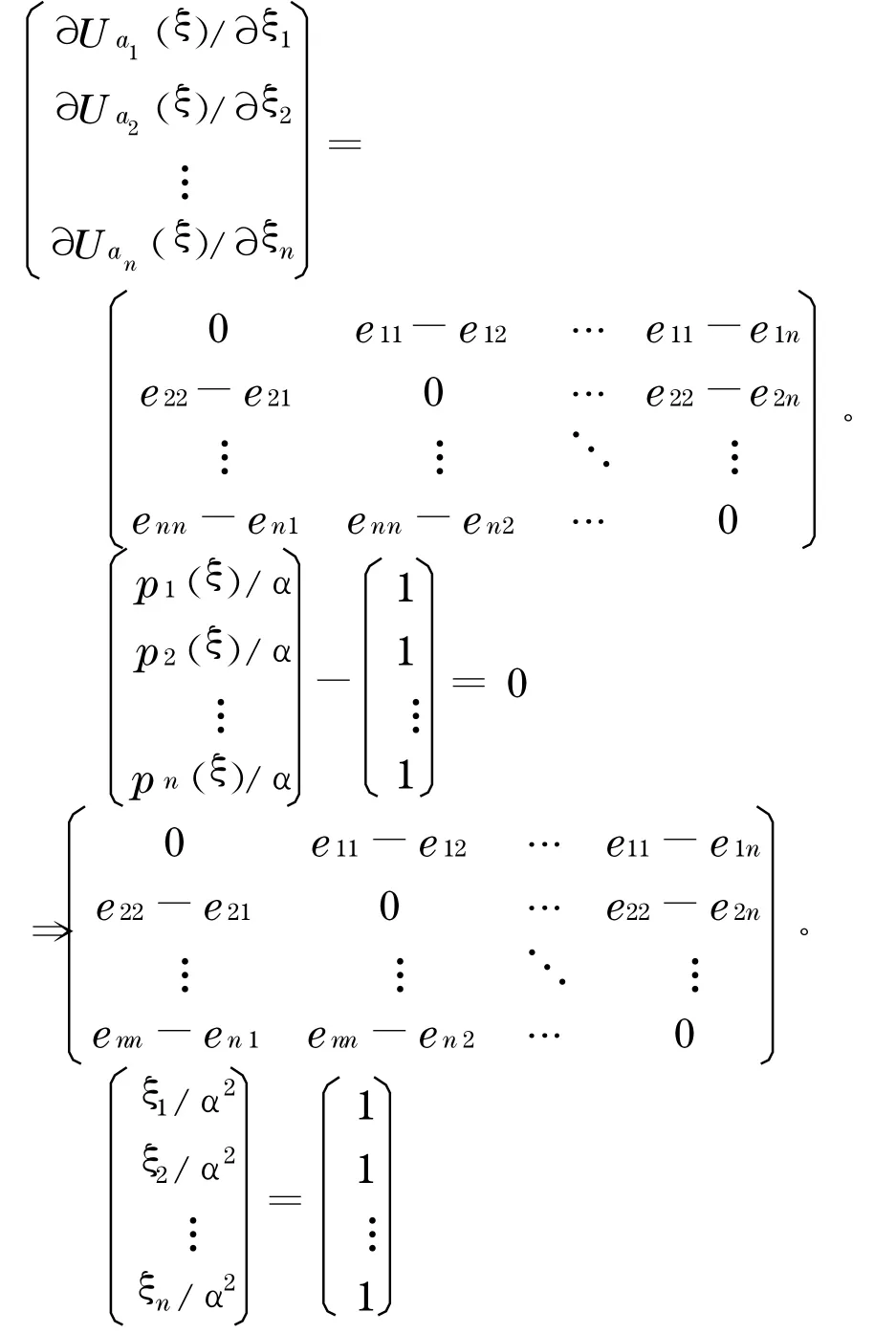
通過(guò)計(jì)算等式兩邊的值, 可以得到Nash 均衡解,雖然計(jì)算比較復(fù)雜, 但通過(guò)Matlab 編程可簡(jiǎn)化計(jì)算過(guò)程.為了簡(jiǎn)化分析過(guò)程, 接下來(lái)以三位房地產(chǎn)開發(fā)商a1,a2,a3的尋租博弈為例進(jìn)行研究.

2.2 均一估值分析

對(duì)于房地產(chǎn)開發(fā)商而言, 土地尋租的效益決定了開發(fā)商付出的程度, 如果對(duì)于獲得土地開發(fā)權(quán)的博弈中開發(fā)商具有相同的效益期望, 則可以通過(guò)以下形式進(jìn)行分析:

假設(shè)三位開發(fā)商a1 ,a2 ,a3 對(duì)土地尋租的價(jià)值判定分別為

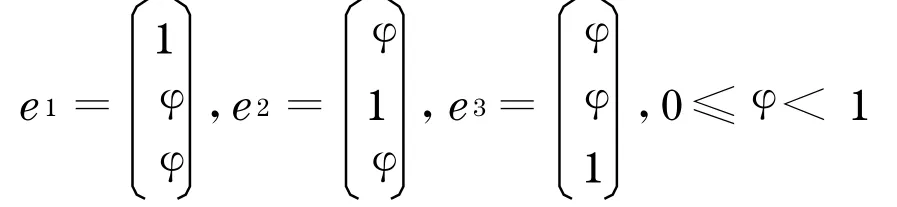
于是三位開發(fā)商的效用函數(shù)可以表達(dá)如下:

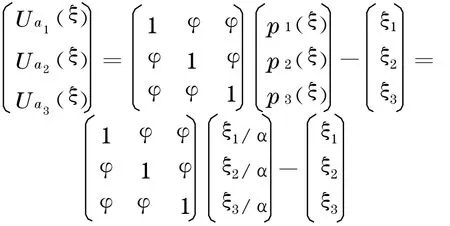
為了得到Nash 均衡解, 對(duì)U i(ξ)求偏導(dǎo)可得均衡條件如下:

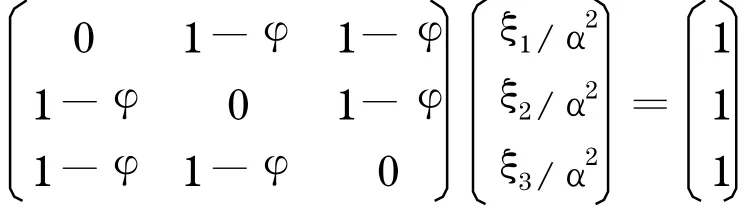
通過(guò)矩陣運(yùn)算可以得到:

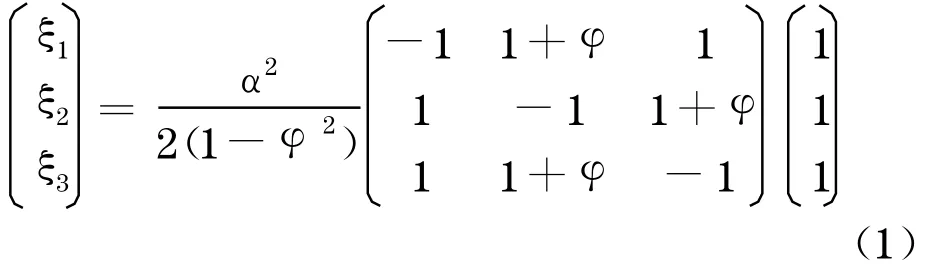
由于

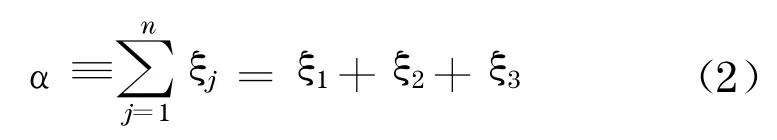
由式(1)和式(2)可求得:

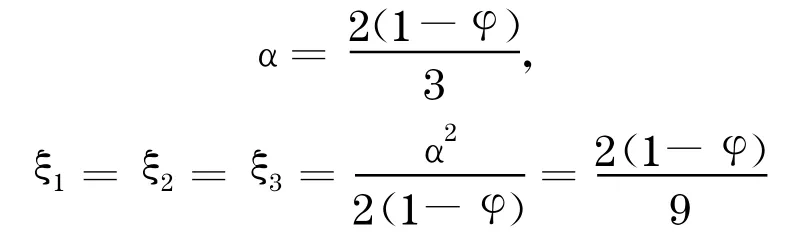
如果令φ=0 ,可以得到Tullock 最初的博弈模型,每位開發(fā)商的支付均衡為2/9,三位開發(fā)商總共的支付配置為2/3 .而在此模型中, 開發(fā)商的尋租博弈的單個(gè)支付和總體支付都下降,從dα/dφ=-2/3＜0 可以看出,開發(fā)商支付總的增長(zhǎng)為負(fù), 也就說(shuō)開發(fā)商在相同效益期望的情況下的尋租博弈均衡總體支付下降.同時(shí),個(gè)體支付也下降,

從均一估值的分析可以看出, 如果開發(fā)商對(duì)于土地尋租具有相同的效益期望時(shí), 個(gè)體和總體的支付都將下降, 這將節(jié)約社會(huì)資源, 減少不必要的消耗.但從社會(huì)實(shí)際看,由于開發(fā)商個(gè)體及所處環(huán)境的差異使得這種均一估值不太可能出現(xiàn), 更多的是如下所分析的差異估值情形.

2.3 差異估值分析

如果開發(fā)商對(duì)于獲得土地開發(fā)權(quán)的效益期望不同,此時(shí)博弈的均衡策略將發(fā)生變化,這里還是以三家房地產(chǎn)開發(fā)商a1,a2,a3作為分析的對(duì)象以簡(jiǎn)化計(jì)算過(guò)程.假設(shè)a1 ,a2 ,a3 認(rèn)為自己能獲勝的期望值分別為:e11,e22,e33,而a1認(rèn)為a2能獲得開發(fā)權(quán)的期望值為φe11(0 ≤φ＜1),a2認(rèn)為a1能獲得開發(fā)權(quán)的期望值為φe22(0 ≤φ＜1),a3認(rèn)為a1和a2獲勝的期望值為零,于是便形成了不同環(huán)境下的對(duì)稱尋租博弈,可以得到期望值矩陣為

于是其效用函數(shù)可以表達(dá)如下:

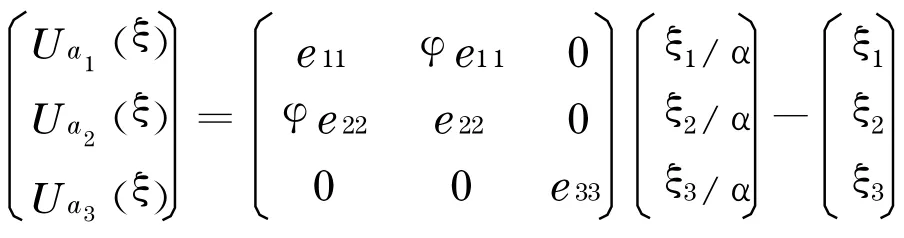
為得Nash 均衡解,對(duì)U i(ξ)求偏導(dǎo)得均衡解為

從式(3)～(6)可以看出, 只有所有開發(fā)商參與才能形成一個(gè)有效的均衡.若式(3)～(5)中有負(fù)值存在,則該開發(fā)商不會(huì)參與尋租博弈,所以必須確保式(3),(4),(5)為正值.在這里需要進(jìn)一步分析在何種情況下開發(fā)商都會(huì)加入尋租博弈中, 這里分兩種情況進(jìn)行討論:

(1)情況一:假設(shè)此時(shí)a1和a2已參與尋租博弈中, 而a3正考慮是否參與其中, 如果a3的期望的邊際收益為正, 即?U a3(ξ1,ξ2,ξ3)/?ξ3＞0 ,a3會(huì)認(rèn)為付出努力是值得的.則a3愿意參與的條件是:

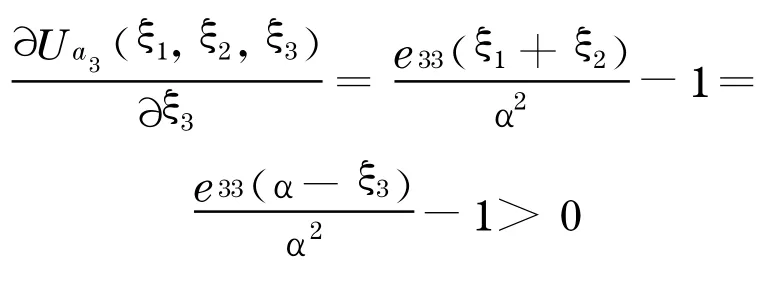
如果a3 不愿意加入博弈, 則有ξ3 =0 ,于是由式(5)有而為a1和a2博弈均衡的總期望值.在這種情況下,如果要吸引a3加入尋租博弈中來(lái), 則必需有:e33＞,當(dāng)φ=0 時(shí),可以看出a3只有在其預(yù)期值大于a1 和a2 估值的平均值時(shí)才愿意加入.

(2)情況二:假設(shè)此時(shí)a1 和a3 已參與尋租博弈中, 而a2正考慮是否參與, 如果a2的期望的邊際收益為正, 即?U a2(ξ1,ξ2,ξ3)/?ξ2＞0 ,a2會(huì)認(rèn)為付出的努力是值得的.則a2愿意參與的條件是:

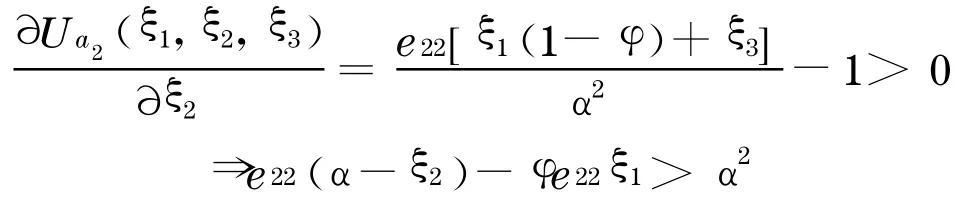
如果a2不愿意加入博弈, 則有ξ2=0 ,于是由式(4)有而為a1和a3博弈均衡的總期望值.在這種情況下, 如果要吸引a2加入尋租博弈中來(lái), 則必需有:e22＞,當(dāng)φ=0 時(shí),可以看出a2只有在其預(yù)期值大于a1和a3估值的平均值時(shí)才愿意加入.如果a1和a3對(duì)尋租博弈的期望值有所提高, 則a2也必需提高期望值來(lái)達(dá)到加入博弈的目的.

從差異估值的分析可以看出, 當(dāng)市場(chǎng)上存在兩位開發(fā)商參與尋租博弈時(shí), 只有當(dāng)?shù)谌邔?duì)于土地價(jià)值的期望值大于前兩位開發(fā)商的平均值時(shí), 他才會(huì)愿意加入博弈.也就是說(shuō),第三者的加入受到前兩位開發(fā)商期望值的約束.同理可以推廣到第N位開發(fā)商的情況,其加入博弈的條件受到前N-1 位開發(fā)商的平均期望值的約束.

3 尋租博弈均衡策略

從上面的分析可以看出,a1,a2,a3對(duì)于主動(dòng)參與博弈的最小期望值分別為

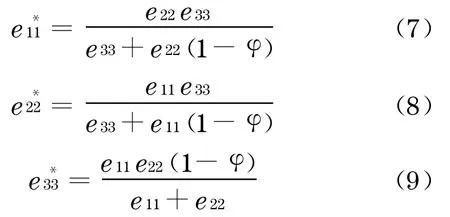
于是每位開發(fā)商的均衡策略可表示為

(1)開發(fā)商a1 的均衡策略如下:

①當(dāng)eii＞e*ii,i∈{1,2 ,3}時(shí),

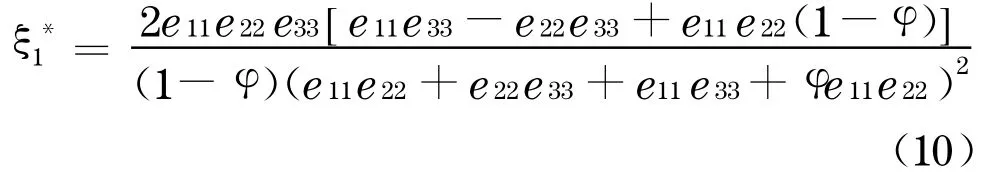
②當(dāng)e22≤e2*2時(shí),

③當(dāng)e33 ≤e3*3時(shí),

④當(dāng)e11≤e1*1時(shí), ξ1*=0 .

(2)開發(fā)商a2的均衡策略如下:

①當(dāng)eii＞e*ii,i∈{1,2 ,3}時(shí),

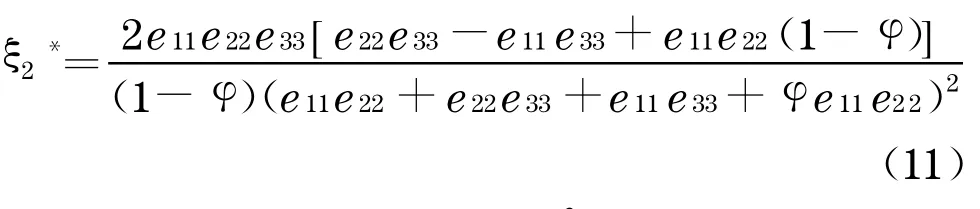
②當(dāng)e11≤e1*1時(shí),

③當(dāng)e33≤e3*3時(shí),

④當(dāng)e22≤e2*2時(shí), ξ2*=0 .

(3)開發(fā)商a3的均衡策略如下:

①當(dāng)eii＞e*ii,i∈{1,2 ,3}時(shí),

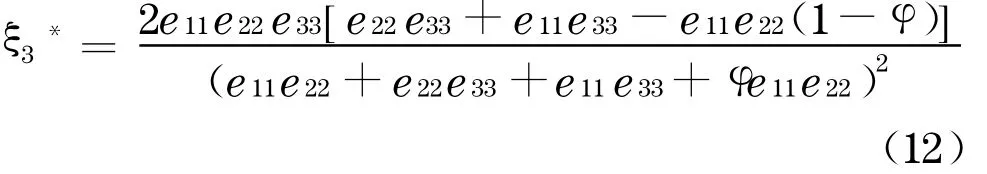
②當(dāng)e11≤e1*1時(shí),

③當(dāng)e22 ≤e2*2時(shí),

④當(dāng)e33≤e3*3時(shí), ξ3*=0 .

在此尋租博弈中,若假設(shè)所有開發(fā)商都會(huì)積極加入競(jìng)爭(zhēng),于是對(duì)a1,a2,a3的行動(dòng)進(jìn)行比較, 可以發(fā)現(xiàn), 若a1和a2認(rèn)為對(duì)方獲勝的概率比較大,即:增大φ值, 則對(duì)于競(jìng)爭(zhēng)中所產(chǎn)生的期望支付ξ*1,ξ*2,α*則會(huì)減小, 而此時(shí)a3的期望支付ξ*3則會(huì)增加.

由于:

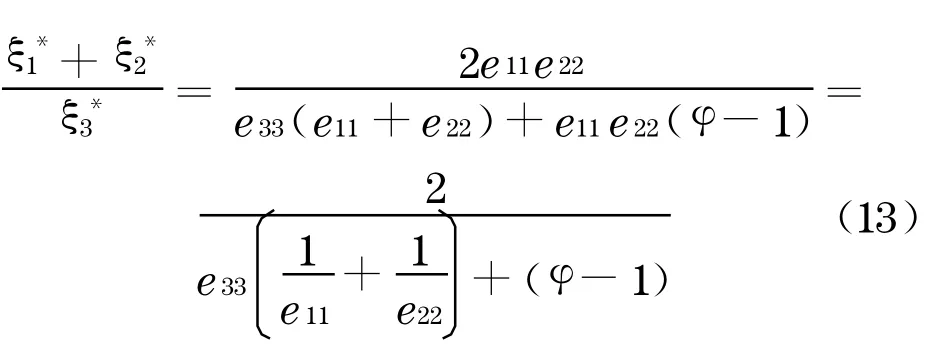
從式(13)中可以看出, ξ*1+ξ*2與e11,e22成正比,而與e33,φ成反比;而ξ*3與e11,e22成反比, 而與e33,φ成正比.

目前對(duì)尋租博弈研究的應(yīng)用模型通常為古諾模型及Stackelberg 模型,古諾尋租博弈在假定租金嚴(yán)格為正,博弈雙方對(duì)于可競(jìng)爭(zhēng)租金具有相同估值,通過(guò)區(qū)分各自的支付函數(shù),在一階效用最大化條件下完成古諾均衡的策略選擇,而Stackelberg 尋租博弈中的博弈雙方對(duì)于租金擁有不對(duì)稱估值,通過(guò)比較無(wú)差異曲線的斜率發(fā)現(xiàn),率先行動(dòng)者將可能有一個(gè)更高的期望支付.相比之下,Stackelberg 模型對(duì)于不完全信息條件下的尋租博弈分析具有更為重要的現(xiàn)實(shí)意義.本文所使用的方法則是基于Stackelberg 尋租博弈思想的延伸,在拓展Tullock 模型的基礎(chǔ)上,基于土地開發(fā)的不同效益期望, 得到了尋租博弈的有效均衡策略, 通過(guò)改變?chǔ)罩悼梢詫?shí)現(xiàn)尋租博弈均衡的轉(zhuǎn)移, 從而有選擇地引導(dǎo)博弈均衡策略的實(shí)現(xiàn).

4 實(shí)例分析

假設(shè)一個(gè)區(qū)域內(nèi)有三家房地產(chǎn)開發(fā)商a1,a2,a3,他們認(rèn)為自己能獲勝的期望值分別為:e11=6 ,e22=8 ,e33=10 ,而a1認(rèn)為a2能獲得開發(fā)權(quán)的期望值為φe11=0 .5 ×6 =3(φ=0 .5),a2認(rèn)為a1能獲得開發(fā)權(quán)的期望值為φe22=0 .5 ×8 =4(φ=0 .5),a3認(rèn)為a1和a2獲勝的期望值為零, 于是便形成了不同環(huán)境下的對(duì)稱尋租博弈, 可以得到期望值矩陣為

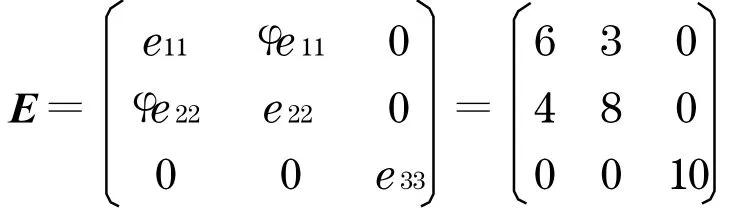
由式(7)～(9)可得:

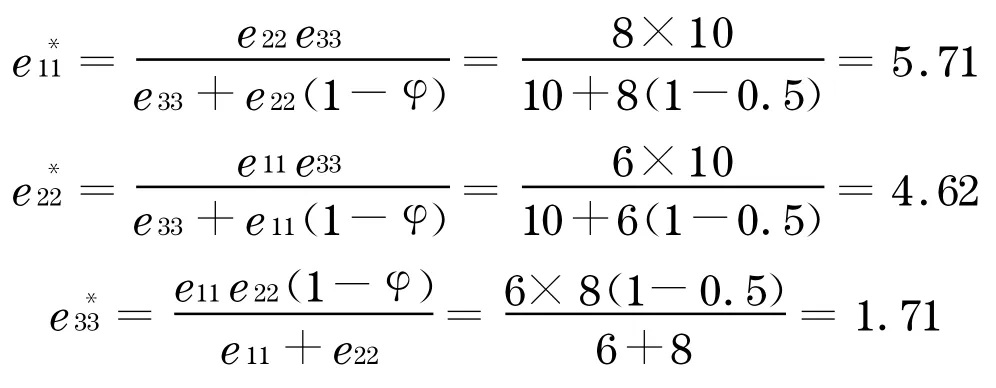
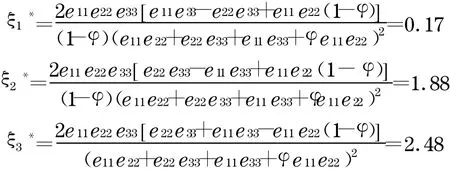
由以上計(jì)算可知:在a1 ,a2 ,a3組成的開發(fā)商中,a1,a2,a3都會(huì)積極地加入尋租博弈中來(lái),而a1的期望支付最小,a3的期望支付最大, ξ*3＞ξ*2＞ξ*1,由可知:在同等期望支付的條件下,a3獲勝的概率較小,而a1獲勝的概率較大.

接下來(lái)改變?chǔ)罩?博弈的均衡策略將發(fā)生重大變化.假設(shè)開發(fā)商a1存在誠(chéng)信問(wèn)題,而開發(fā)商a2對(duì)社會(huì)的貢獻(xiàn)較突出,此時(shí)希望尋租博弈均衡向a2傾斜, 則可增大φ值,取φ=0 .8 ,期望值矩陣變化如下:

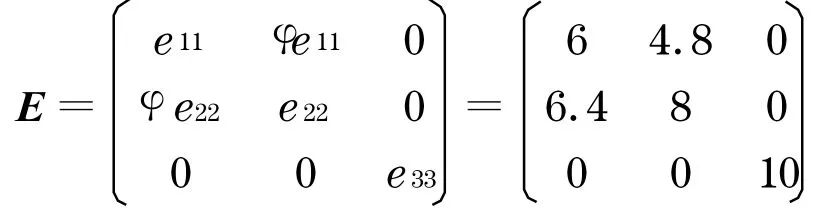
由式(7)～(9)可得:e*11=6 .90 ,e*22=5 .36 ,e*33=0 .69.由于,e11≤e*11,由前面第3 節(jié)的分析可知:ξ*1=0 ;.可以看出,在該尋租博弈中實(shí)際的支付總值ξ*1+ξ*2+ξ*3下降了,社會(huì)資源得到節(jié)約.由于開發(fā)商a1的實(shí)際期望值達(dá)不到參與博弈的最小期望值,即:e11≤e*11,故a1將淡出尋租競(jìng)爭(zhēng),而在開發(fā)商a2與a3的競(jìng)爭(zhēng)中,ξ*2＜ξ*3,故在同等期望支付的條件下,a3獲勝的概率較小,而a2獲勝的概率較大.可見,通過(guò)增大φ值,使尋租博弈的均衡策略發(fā)生轉(zhuǎn)移,有利于社會(huì)公平的實(shí)現(xiàn).

5 結(jié)論

在房地產(chǎn)領(lǐng)域,開發(fā)商以自身利益最大化為目標(biāo),為獲取土地的開發(fā)權(quán)而實(shí)施尋租,開發(fā)商的尋租行為會(huì)帶來(lái)利益競(jìng)爭(zhēng),損害社會(huì)公平,最終會(huì)將尋租成本傳遞到房地產(chǎn)的市場(chǎng)定價(jià)上.本文在經(jīng)典Tullock 尋租博弈模型的基礎(chǔ)上,考慮到開發(fā)商對(duì)于土地價(jià)值期望的不同,利用期望矩陣擴(kuò)展了尋租博弈的應(yīng)用范圍.并分析了均一估值和差異估值下的博弈均衡的變化,得到了尋租博弈的有效均衡策略.該模型是對(duì)房地產(chǎn)開發(fā)商土地尋租博弈的有益嘗試,可以預(yù)測(cè)博弈的結(jié)果,通過(guò)改變?chǔ)罩悼梢愿淖儗ぷ獠┺牡木?從而有選擇地引導(dǎo)博弈均衡策略向有利于社會(huì)公平方向轉(zhuǎn)移.

[1] Tullock G .Efficient rent-seeking :toward a theory of the rentseeking society [M] .[S .l .] :Tex as A & MUniversity Press, 1980.

[2] Perez-Castrillo J D, Verdier T .A general analy sis of rentseeking games[J] .Public Choice,1992, 73(3):335.

[3] Bruce G L .Stackelberg rent-seeking[J] .Public Choice, 1993,77(2):307.

[4] Bruce G L .Cooperative rent-seeking[J] .Public Choice, 1994,81(1-2):23.

[5] Skaperdas S,Gan L.Risk aversion in contests [J] .The Economic Journal, 1995, 105:951.

[6] Szidarovszky F, Okuguchi K .On the existence and uniqueness of pure Nash equilibrium in rent-seeking games[J] .Gam es and Economic Behavior,1997, 18(1):135.

[7] William E S .Asymmetric rent-seeking with more than two contestants[J] .Public Choice, 2002, 113(3-4):325.

[8] Cornes R, Hartley R.Risk aversion, heterogeneity and contests[J] .Public Choice,2003, 117(1-2):1.

[9] David A M, Andrew J Y .Equilibria in rent-seeking contests with homogeneous success functions[J] .Economic Theory ,2006, 27(3):719.

[10] Matros A .Rent-seeking with asymmetric valuations:addition or deletion of a player [J] .Public Choice, 2006, 129(3-4):369.

[11] Riechmann T .An analy sis of rent-seeking games with relativepayoff maximizers[J] .Public Choice, 2007, 133(1-2):147.

[12] Yamazaki T . The uniqueness of pure-strategy Nash equilibrium in rent-seeking games with risk-averse players[J] .Public Choice, 2009, 139(3-4):335.

[13] Yamazaki T .On the existence and uniqueness of pure-strategy Nash equilibrium in asymmetric rent-seeking contests[J] .Journal of Public Economic Theory,2008, 10:317.

[14] Matros A,Armanios D . Tullock ' s contest with reimbursements[J] .Public Choice,2009, 141(1-2):49.

[15] Schoonbeek L .Bribing potential entrants in a rent-seeking contest[J] .Public Choice, 2009, 139(1-2):153.

[16] 王斌, 徐寅峰, 李志敏.尋租現(xiàn)象監(jiān)督治理的不完全信息動(dòng)態(tài)博弈分析[J] .系統(tǒng)工程, 2005, 23(10):81.WANG Bin, XU Yinfeng,LI Zhimin .A dynamic game analysis on disposal of rent-seeking phenomina with incomplete information[J] .Systems Engineering,2005, 23(10):81.

[17] 華武, 繆柏其.戰(zhàn)略聯(lián)盟尋租博弈分析[J] .中國(guó)管理科學(xué),2002, 10(3):18.H UA Wu,MIAO Baiqi .Analysis on stackelberg rent-seeking games in the strategic alliance [J] .Chinese Journal of Management Science,2002, 10(3):18.

[18] David A M, Andrew J Y .Equilibria in rent-seeking contests with homogeneous success functions[J] .Economic Theory ,2006, 27(3):719.

[19] Skaperdas S .Contest success functions[J] .Economic Theory ,1996, 7(2):283.