Dual-wavelength pumped latticed Fermi–Pasta–Ulam recurrences in nonlinear Schr¨odinger equation
Qian Zhang(張倩), Xiankun Yao(姚獻(xiàn)坤),2,3,?, and Heng Dong(董恒)
1School of Physics,Northwest University,Xi’an 710127,China
2Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China
3Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China
Keywords: modulation instability,dual-wavelength pumps,latticed-Fermi-Pasta-Ulam recurrences
1.Introduction
In the past, modulation instability (MI) has been extensively studied in many areas including Bose-Einstein condensate,[1,2]hydrodynamics,[3]nonlinear fiber optics[4]and plasma physics,[5]etc.It is associated with the growth of perturbated on a continuous-wave background,[6]and is also the key mechanism in the development of a variety of complex patterns, such as Akhmediev breathers(ABs),[7-9]Fermi-Pasta-Ulam (FPU) recurrences,[10-12]superregular breathers,[13-15]Kuznetsov-Ma breathers,[16,17]and rogue waves.[18-21]Through linear stability analysis, MI in the initial stage reflects the exponential growth of the spectral sideband perturbation until MI enters a nonlinear stage when the growth reaches saturation, and the wave dynamics exhibit a complex frequency conversion process.[22,23]The multi-wave truncation method[24-27](MWT)has been used to analyze the dynamics of MI in various systems,including birefringence fibers,[23,28]the dispersion-oscillating fibers,[29,30]the pure-quartic dispersion systems,[22]and the dissipative systems.[31-33]The method only considers the interaction between the pump and the first-order sidebands, and ignores the influence of the higher-order sidebands.The heteroclinic structure[34](i.e.,Hamiltonian contour line on the phase-space plane)obtained by the mode truncation method reveals all possible dynamic trajectories of nonlinear waves.
MI can exist not only on the aforementioned plane wave background, but also on the modulated-wave background.[35-37]Modulated wave is equivalently viewed as the superposition of two plane waves of different frequencies.In general, the coupled nonlinear Schr¨odinger equation (CNLSE) is used to describe the perturbation of dual-wavelength pumps case.[38]However, the MI of dualwavelength pumps described in CNLSE does not intuitively reflect dual-wavelength characteristics, and some specific physical phenomena are lost by neglecting the four-wave mixing term in the process.
In this paper,we address this issue and comprehensively analyze the MI of dual-wavelength pumps by using NLSE with an approximate stationary solution, representing a modulated wave.Firstly, the linear stage of MI is analyzed by linear stability analysis.Subsequently, a complicated heteroclinic structure is obtained by the MWT method.We also show that different FPU recurrences are separated by separatrix on the heteroclinic structure.In addition, we report the occurrence of latticed-FPU patterns excited on the modulated-wave background in NLSE.
2.Physical model and linear stability analysis
The propagating dynamic of light is governed by the following dimensionless NLSE:
whereψis the normalized field.zandtare normalized distance and time,respectively.
It is well known that the nonlinear process of energy exchange between four equidistant and symmetric frequency components of the field in NLSE can be solved exactly by Jacobi elliptic functions.[39]In this paper, when the frequency difference of the dual-wavelength is large enough, it is feasible to approximate the elliptic-function solution as a cosine function,which is convenient and effective to analyze the MI of dual-wavelength.It reads

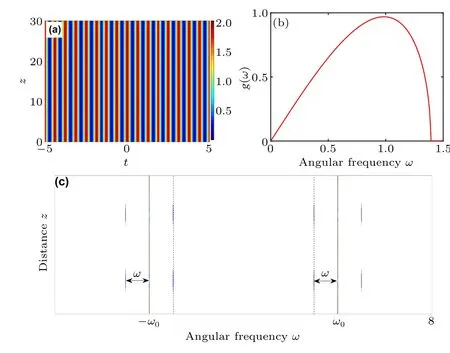
Fig.1.(a)Temporal evolutions of the total intensity|ψ0|2 with ω0 =5.(b)MI gain spectrum profile for Eq.(1)at ω0 =4.(c)Schematic representation of MI produced by dual-wavelength pump(dashed vertical lines label the first-order sidebands,ω stands for modulation frequency).Here,P=1.
3.Multi-wave truncation model and heteroclinic structure
Although linear stability analysis can be used to predict the initial stage of instability,it could not provide any further insight into the long-term behavior of the system.However,important insights into dynamics can be gained by using the MWT method.Here, only dual-wavelength pumps and their respective±1 order sidebands are considered, with frequencies±ω0,±ω0-ω, and±ω0+ω, respectively.The two sets of nonlinear local waves with different frequencies have the same evolution properties except for the different group velocities.Therefore, based on the physical process of dualwavelength pump propagation, we construct the breather solution of Eq.(1),which has a unique form as follows:
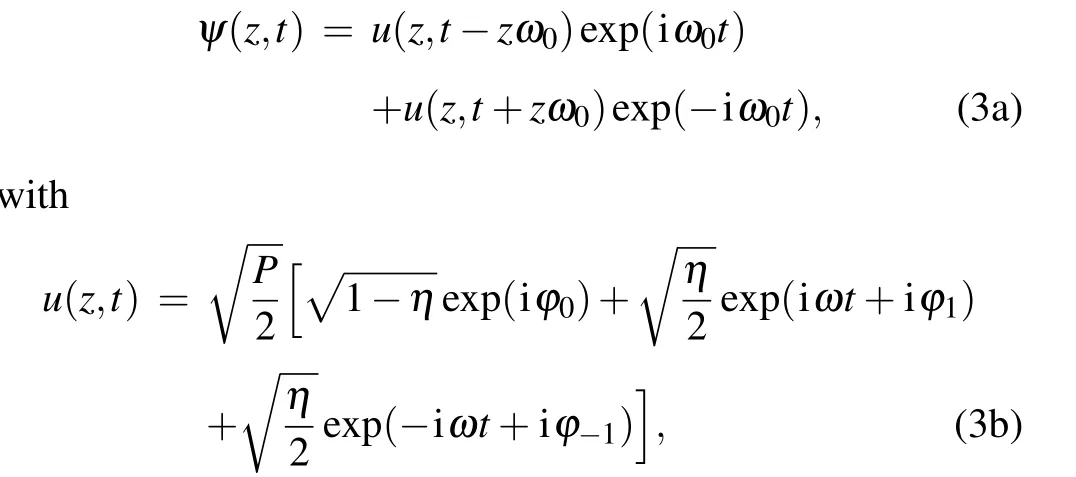
where Eq.(3a) describes the dynamic process of cross-phase modulation of dual-wavelength pumps by a simple expression.u(z,t)is the wave function obtained by dual-wavelength pumps under the relatively stationary coordinate of their propagation when the group velocity is zero.φ0(z)andφ±1(z)are the pump and sidebands phases, andη(z) is the total power of the first-order sidebands.Assuming the total power fraction of the field in Eq.(1) is equal to 1, it is convenient to define the sidebands fractionηand pump fraction 1-η.ωcis the critical frequency,which is the crossed point of the stable branch of Δφe=π/2(black solid line)and the unstable branch ofηe=1(red dash line)as shown in Fig.2(a).The frequencyωis henceforth limited toωc<ω <ωmaxto effectively prevent higher-order MI from occurring.Substituting Eq.(3)into Eq.(1),the Hamiltonian form of the nonlinear wave evolution is obtained as follows:
where the dot denotes derivation with respect tozand Δφ= (φ1+φ2-2φ0)/2 is the effective phase.Q(z) =1 + 2cos(2ωω0z) andS(z) = (3/2) + 4cos(2ωω0z)-cos(4ωω0z).It is evident that the Hamiltonian functionHexhibits periodic behavior, indicating that it is not a conserved quantity.As a result, it is unable to construct a phase space diagram forH.To resolve the problem,we take the average ofH.The average Hamiltonian ˉHreads
The average Hamiltonian ˉHcan be described as contours on the (Δφ,η) phase plane as shown in Fig.2(b), where all possible dynamic trajectories of MI at frequencyωare given.Obviously,the contours of ˉHhave a heteroclinic structure,and there is a separatrix(see the closed black line in Fig.2(b))that divides the phase plane into regions of inner and outer orbits.The evolution of MI can be comprehensively analyzed from the phase plane portrait of ˉH.
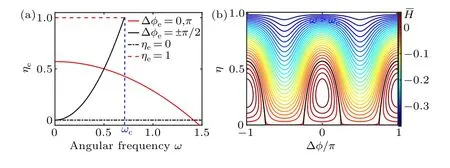
Fig.2.(a)Stationary sideband fraction ηe of stable(solid lines)and unstable(dash and dash-dotted lines)branches versus ω beyond ωc.(b)Average Hamiltonian contours on the phase plane (Δφ,η) for ω =1.The black curve is heteroclinic separatrix with ηe =1, dividing the phase plane into two different domains.Here,P=1,ω0=4 and ωc=(P/2)1/2.
Equation (5) has four groups of stationary points(Δφe,ηe) (solutions of dη/dz= dΔφ/dz= 0) corresponding to four eigenmodes.Figure 2(a) shows the bifurcation diagram, i.e., the valueηeof the stationary points versus frequencyω.In the gain range that we have studied, only heteroclinic separatrix with stationary pointsηe=0 is considered.In this case,the heteroclinic structure follows the well-known structure of the integrable NLSE.[25,34]Hence,we have disregarded the two stationary points of(Δφe,ηe)=[π/2,2ω2/P]and(Δφe,ηe)=[0.5cos-1(-(ω2/P)-0.5),1].There are only two stationary points directly related to the heteroclinic structure here.
One of the group stationary points of (Δφe,ηe)=[0 orπ,-(2ω2/7P)+(4/7)] corresponds to the maxima of ˉH.This eigenmode is stable because the contour of ˉHshrinks to the point (Δφe,ηe) when the Hamiltonian ˉHreaches its extreme value.The red solid line in Fig.2(a) gives the relationship between the sideband fractionηeand modulation frequencyω.Only if the input condition satisfies ˉH(Δφe,ηe)=(ω4/14P)-(ω2/2)+(2P/7), it will evolve asymptotically toward such eigenmode.
Another group stationary points of (Δφe,ηe) =[±0.5cos-1(-(ω2/P)-1),0] suggest unstable eigenmodes and turn out to be the bottom vertexes of the contour ˉHin the frequency range ofω <ωmax,which agrees with the MI gain bandwidth from linear stability analysis.It is worth noting that the contour of ˉH=0 composes the heteroclinic separatrix,on which the latticed ABs can be excited.Strictly speaking,only if the input condition satisfies ˉH(Δφ0,η0)=0, the nonlinear wave evolution pattern of Eq.(3)belongs to the latticed ABs.However,the interaction between the dual-wavelength pumps induced by the cross-phase modulation, results in the generation of extra optical waves.As a consequence, the latticed ABs cannot be excited and can only obtain FPU recurrence evolution,as shown in Fig.3(a).
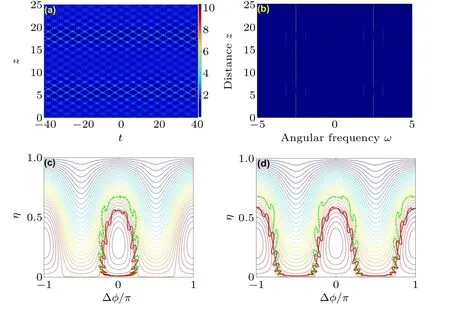
Fig.3.Latticed ABs recurrent evolution through numerical integration of Eq.(1)with η0=0.01.Panels(a)and(b)show the temporal and spectral evolutions of the total intensity|ψ(z,t)|2.Panels(c)and(d)show the corresponding projections of Eq.(1) (green dash-dotted line), Eq.(4a) (red solid line),and Eq.(5)(black dotted lines)on the phase plane(Δφ,η)for(c)Δφ0=0 and(d)Δφ0=π/2.Here,P=1,ω0=4,and ω =1.
4.Latticed-Fermi–Pastel–Ulam recurrences
The bifurcations illustrated in Fig.2 have a profound influence on the long-term evolution of the nonlinear wave in Eq.(1).In order to show this,we numerically integrate Eq.(1)by taking the modulated dual-wavelength pumps as the initial condition
whereη0is the initial sidebands fraction,and Δφ0is the overall initial effective phase Δφ0=Δφ(0).
Next,we illustrate the nonlinear wave evolutions and dynamic trajectories inside and outside the heteroclinic separatrix forω >ωc.Because there is no essential difference in the latticed ABs patterns we obtained under two different initial effective phase conditions, only one of the recurrent regimes is shown in Figs.3(a) and 3(b), where Δφ0=0.However,the projection of Eq.(1)evolved onto the phase space reveals very different behaviors for the two initial effective phase conditions.Figures 3(c)and 3(d)depict their dynamic trajectories with the initial phases of Δφ0=0 and Δφ0=π/2.All three trajectories are obtained in the numerical results from Eq.(1)(green dash-dotted line), Eq.(4a) (red solid line) and Eq.(5)(black dotted lines),respectively.One can see that the numerical results by Eq.(4a) are significantly different from those by Eq.(5) induced by neglecting the four-wave mixing process.The dynamic trajectory obtained by integrating Eq.(4a)oscillates with the evolution ofz.Meanwhile, Eqs.(4a) and(1) also exhibit deviations due to the neglect of higher-order sidebands.
Theoretically,the above Figs.3(a)and 3(b)behaviors correspond to different spatiotemporal evolution.To prove it,under such an input condition of Eq.(6),we utilize the split-step Fourier transform method to implement the numerical integration of Eq.(1).Then, we filter the spectrum ofψ(z,t)to obtain the optical-wave evolution ofu(z,t).Actually,in order to extractu(z,t)from Eq.(3),we perform a coordinate transformation on it.Finally, we obtain the unshifted and staggered FPU recurrences under two initial phase conditions,as shown in Fig.4.Figure 4(a) shows that the FPU recurrence drift is caused by the Kerr nonlinear effect.This phenomenon arises from the acute variation in the nonlinear refractive index of the medium under the nonlinear superposition of two optical intensities.Furthermore,the two patterns shown in Fig.4 correspond to the orbit in Figs.3(c)and 3(d),respectively.
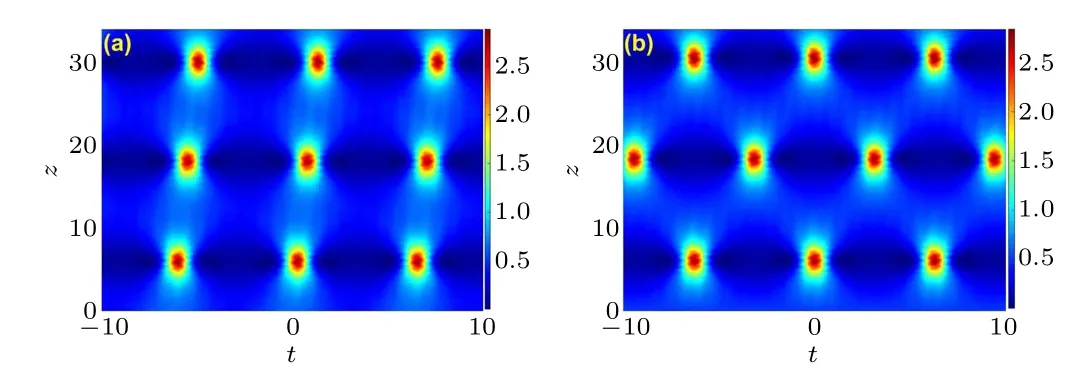
Fig.4.Two types of FPU evolutions through numerical integration of Eq.(1)with initial effective phases:Δφ0=0(unshifted)(a)and Δφ0=π/2(staggered)(b).The above temporal evolution of the intensity is|u(z,t)|2.All parameters are the same as in Fig.3.
5.Conclusion
We study numerically the nonlinear stage of the modulation instability of the dual-wavelength pumped in the framework of the nonlinear Schr¨odinger equation.It is interesting to note that,NLSE has an approximate stationary solution which is linearly superimposed by two plane wave solutions.The existence condition of the solution is given and confirmed by numerical simulation.Dramatically,we show that the latticed-FPU recurrences can be excited on the modulated-wave background in NLSE.These results further enrich the types of nonlinear local waves.From our work,we hope to further broaden and deepen the understanding of MI.
Acknowledgments
Project supported by the National Natural Science Foundation of China (NSFC) (Grant No.12004309), the Shaanxi Fundamental Science Research Project for Mathematics and Physics (Grant No.22JSQ036), and the Scientific Research Program funded by Shaanxi Provincial Education Department(Grant No.20JK0947).
- Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry

