Remote entangling gate between a quantum dot spin and a transmon qubit mediated by microwave photons
Xing-Yu Zhu(朱行宇), Le-Tian Zhu(朱樂(lè)天), Tao Tu(涂濤),3,?, and Chuan-Feng Li(李傳鋒),3,?
1Key Laboratory of Quantum Information,Chinese Academy of Sciences,University of Science and Technology of China,Hefei 230026,China
2School of Mechanical and Electronic Engineering,Suzhou University,Suzhou 234000,China
3Hefei National Laboratory,University of Science and Technology of China,Chinese Academy of Sciences,Hefei 230088,China
Keywords: hybrid quantum architectures,circuit quantum electrodynamics,entangling gate
1.Introduction
Hybrid architectures are a promising route to scalable quantum processors, as they would benefit from the advantages of different qubits.Semiconductor spin qubits and superconducting qubits are the two main candidates for solid-state qubits because of their compatibility with modern microelectronics and thus the advantages of large-scale integration.[1,2]Spin qubits have the advantage of small footprint and long coherence time,[3–6]while superconducting qubits have the advantage of fast, high-fidelity gate operations.[7–9]It is desirable to use hybrid architectures to combine the advantages of the different systems.However, scalable hybrid quantum architectures require a coherent link that entangles any two different solid-state qubit systems.
Circuit quantum electrodynamics(circuit-QED)provides an attractive way to implement such link by utilizing microwave photons in a superconducting resonator as a quantum bus coupled to different qubits.[10]Circuit-QED has achieved many important advances in superconducting systems, such as strong coupling to superconducting qubits and serving as a sensitive detector to measure the states of superconducting qubits.[11–14]Recently,spin qubits in semiconductor quantum dots have also realized coherent coupling to microwave photons in circuit-QED.[15–19]However, entanglement of a spin qubit with another distant superconducting qubit has not been demonstrated.High-fidelity remote entanglement is a key element of hybrid architectures and is therefore highly desired,but also challenging.The challenges are that,on the one hand,spin qubits typically require large magnetic fields, to which superconducting qubits are not resistant.On the other hand,solid-state qubits are usually affected by charge noise in circuits, thus requiring the design of suitable working regimes for high-fidelity entangled state preparation.
In this article, we present a complete scheme to overcome these challenges.First, we use a resonant exchange(RX)qubit consisting of three electronic states in a semiconductor triple quantum dot.[20,21]It is capable of all-electrical control in zero magnetic fields and thus can work with superconducting qubits on the same chip.Second, we employ a high-impedance superconducting quantum interference device(SQUID) array resonator as a quantum bus, which is able to couple efficiently with the RX and superconducting transmon qubits.[22–24]In addition, since the operation frequency and coupling strength of the whole hybrid system are tunable,we design a virtual photon exchange scheme,thus demonstrating fast, high-fidelity swap gate operations and remote entangled state preparation between two different qubits under experimental parameters.The fidelity of the entangling gate operations can be as high as 96.5%,which has reached the threshold of various distributed quantum error-correction codes.These results can be applied to various quantum information processes in hybrid architectures.
2.Setup and models
As shown in Fig.1(a), we consider a hybrid architecture consisting of a semiconductor RX spin qubit, a superconducting transmon qubit and a SQUID array resonator.We implement the semiconductor qubit by controlling three electrons in a triple quantum dot(TQD)hosted in silicon material.There are two charge configurations: the symmetric (1,1,1)and the asymmetric(2,0,1)and(1,0,2)configurations.Here(nl,nm,nr) denotes the number of electrons in the left, middle,and right dots,respectively.Typically,three electron spins have eight different spin states (see Appendix A).When we consider the subspace with total spinS=1/2 and total spinzcomponentSz=1/2,there are four relevant spin states

Heretl(tr) is the tunnel coupling between the left (right) dot and the middle dot,ε= [ε(2,0,1)-ε(1,0,2)]/2 and?=ε(1,1,1)-[ε(2,0,1)+ε(1,0,2)]/2 are the asymmetry parameter and the detuning of the TQD, andε(l,m,r) denotes the energy of different charge configurations.
Moreover,we diagonalize the Hamiltonian(2)and focus on the two lowest states|0RX〉and|1RX〉.Now we obtain the RX qubit Hamiltonian
whereωRXis the transition frequency of the qubit andσzis the Pauli operator.Figure 1(b) shows the eigenenergies of the TQD system as a function of parameterε.The nature of the RX spin qubits is fully controlled by the electrical parameterεwithout the need for an applied magnetic field.At the same time, in the regime aroundε=0, the RX qubit becomes first-order insensitive to charge noise(see Appendix B).Note that RX spin qubits have a number of unique advantages.On the one hand, unlike one- and two-electron spin qubits,[1,25–28]which require an external magnetic field, RX spin qubits can operate under zero magnetic fields, which is important for compatibility with superconducting qubits.On the other hand,RX qubits are encoded in a hybridized state of electron charge and spin.Adjusting the TQD electrode voltages, when?> 0, the RX qubits mainly have asymmetric charge configurations and thus large electric dipole moments,which can couple strongly to the resonator.And when?<0,the spin character of the RX qubit increases,which leads to a longer coherence time because it is insensitive to charge noise.
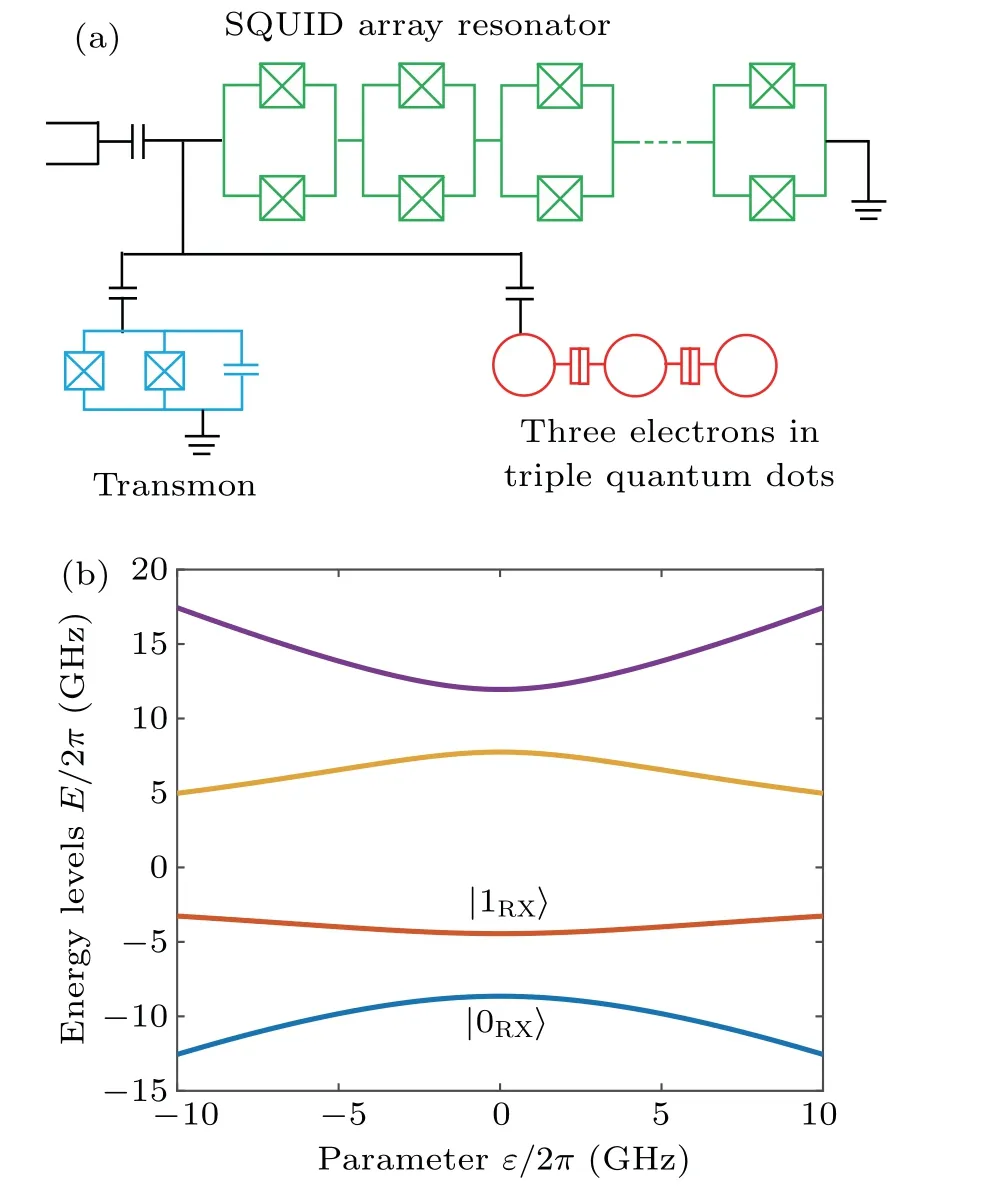
Fig.1.(a) Schematic of the spin–superconducting hybrid architecture.The hybrid system integrates three different quantum systems:a spin qubit in a triple quantum dot and a superconducting transmon qubit, which are coupled to a SQUID array resonator.(b) Eigenenergies of the TQD system as a function of the asymmetry parameter ε for?/2π =-3.3 GHz,and tl/2π =tr/π =8.3 GHz.
The superconducting transmon qubit is formed by a single island capacitor and two parallel Josephson junctions, as shown in Fig.1(a).The superconducting system Hamiltonian can be written as
whereEcandEJare the charging and Josephson energies of the device,ngis the effective offset charge,nand?denote the charge number and phase difference across the junction, respectively.We also diagonalize the Hamiltonian(3)and consider only the two lowest states|0tr〉and|1tr〉,with higher levels omitted due to sufficient anharmonicity.[22]Now we obtain the transmon qubit Hamiltonian
whereωtris the transition frequency of the transmon qubit andσzis the Pauli operator.Note that the transition frequencyωtrcan be adjusted by controlling the flux in the device loop.
The resonator is composed of an array of SQUID loops and the resonator Hamiltonian is given by
wherea?andaare the creation and annilation operators of the resonator.We note that the frequency of the resonatorωSqcan be tuned by the flux in the SQUID loop.In addition, the SQUID array resonator has a high impedance,which can significantly enhance the coupling strength between the resonator and the qubits.
When the resonator is capacitively coupled to the left dot of the TQD, the charge–resonator coupling strength isgch.Since the asymmetric charge configuration|2〉 of the TQD has a larger electric dipole moment, the spin–resonator coupling strength isgRX= 2gchc02c12, where the coefficientsc02=〈2|0RX〉andc12=〈2|1RX〉are a mixture between the RX qubit state and charge configuration|2〉 (see Appendix C).Therefore,in the rotating wave approximation,the interaction between the RX qubits and the resonator is described by the following form:

3.Dispersive regime and entangling gates

the perturbed Hamiltonian is

As shown in Fig.2(a), varying the asymmetry parameterεof the TQD from the larger to the smaller asymmetric configuration, the coupling strengthJbetween the qubits can be significantly increased.This is due to the fact that near the smaller asymmetric configuration (ε= 0), the electrons are delocalized between the quantum dots, which enhances the electric dipole moment and the coupling strength between the RX qubit and the resonator.This further increases the effective coupling strength between the RX qubit and the transmon qubit.

Fig.2.(a)Effective coupling strength between RX and transmon qubits as a function of the asymmetry parameter ε.Here we use the parameters ?/2π=-3.3 GHz,tl/2π=tr/2π=8.3 GHz,ωSq/2π=5.2 GHz,ωtr/2π =4.2 GHz,gch/2π =115 MHz,gtr/2π =200 MHz.(b)Time evolution of the state population of RX and transmon qubits during an iSWP gate.

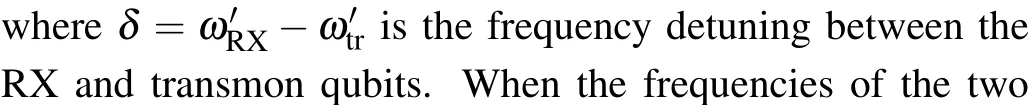
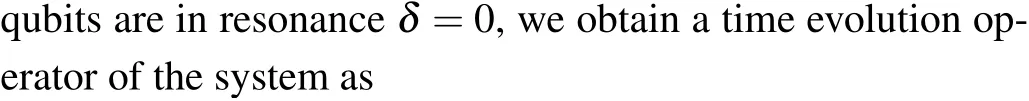

4.Fidelities of entangling gates
We now evaluate the performance of a remote entangling gate between RX and transmon qubits.The dynamics of the hybrid system can be determined by the master equation
whereρis the density matrix of the hybrid system, and the Lindblad operatorD[O]ρ=OρO?-(O?Oρ+ρO?O)/2 describes various decoherence processes.We include the following decoherence parameters: the relaxation and dephasing ratesγl,RX=1/Tl,RXandγφ,RX=1/Tφ,RXfor the RX qubit,the relaxation and dephasing ratesγl,tr=1/Tl,trandγφ,tr=1/Tφ,trfor the transmon qubit, and the photon decay rateκof the resonator.In this study, we use experimental values of these parameters:Tl,RX= 20 ms andTφ,RX= 2.3 μs for the RX qubit,[30,31]Tl,tr=Tφ,tr=60μs for the transmon qubit,[32]andκ=4.6 MHz for the resonator.[24]Note that we consider RX qubits hosted in silicon quantum dots, so that the spin noise due to nuclear spins can be neglected and the charge noise becomes the main source of decoherence of the RX qubits.
As shown in Fig.3(a), we demonstrate a scheme to perform entangling gates between RX and transmon qubits.First,we control the frequencies of RX and transmon qubits in a large detuning regime, in which the interaction between RX and transmon qubits is very weak.Second, we tune the frequencyωRXof the RX qubit and make it resonance with the transmon qubit for a period of timetg.At this stage, there is an effective interactionJ/2π=9 MHz between the RX and the transmon qubits, and the quantum state transfers between the two qubits.Finally,the frequency of the RX qubit is tuned back to the large detuning regime.We calculate the dynamics of an entangling gate under the influence of realistic decoherence in Fig.3(b).We also extract the gate timetg=28 ns from Fig.3(b),which is much shorter than the decoherence time of the RX and transmon qubits.
To evaluate the entangling gates between the RX and transmon qubits, we calculate the average fidelityFof the gate.For all possible initial pure states, we obtain the corresponding final states using the master equation.The average fidelity is determined by the average value of the overlap between the target pure states and the final mixed states[33,34]

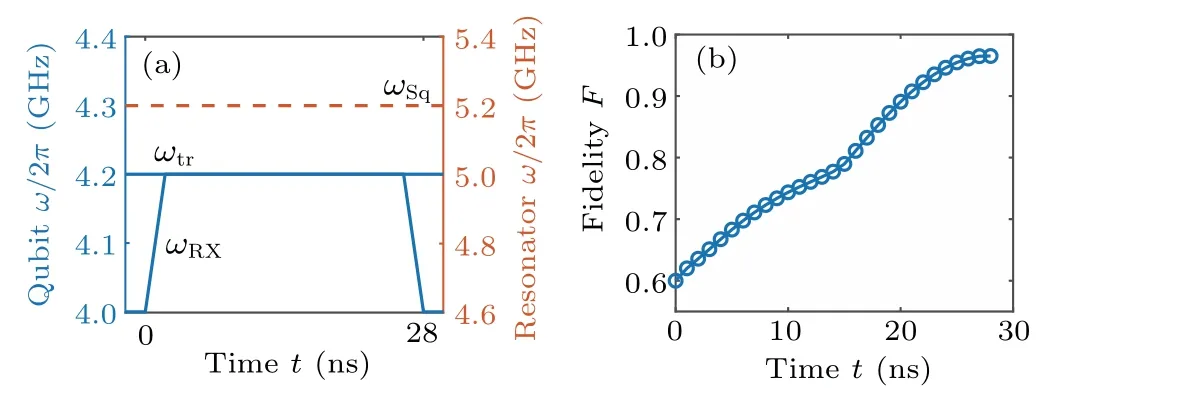
Fig.3.(a)Scheme for realizing an entangling gate by time-dependent control of the RX qubit frequency.(b) Gate fidelity as a function of the gate time t.Here we use the parameters ωSq/2π =5.2 GHz,ωtr/2π = 4.2 GHz, ωRX/2π = 4.0-4.2 GHz, gRX/2π = 45 MHz,gtr/2π =200 MHz.
5.Effects of various control parameters
The fidelity of the entangling gate in the hybrid system is limited by the decoherence processes of the RX qubits,the transmon qubits and the resonator.In Fig.4(a),we find that the entangling gate fidelityFincreases with the relaxation timeTl,RXand dephasing timeTφ,RXof the RX qubits.Compared with the relaxation time, the entangling gate fidelity is more sensitive to the dephasing time.For example, for a fixed relaxation time ofTl,RX=20 ms,the entangling gate fidelity increases rapidly from 87.4%to 96.8%when the dephasing timeTφ,RXchanges from 100 ns to 5μs.This result indicates that the dephasing process of RX qubits is the main limiting factor of this scheme.For the transmon qubits, varying the relaxation timeTl,trand dephasing timeTφ,trfrom 1 μs to 100 μs,the entangling gate fidelity slightly increases from 94.5% to 96.5%,as shown in Fig.4(b).This result is expected because transmon qubits are insensitive to charge noise and have long relaxation and dephasing times.Figure 4(c)shows that the entangling gate fidelity gradually increases as the photon decay rateκdecreases.Due to the Purcell effect in the hybrid system, the photon decay of the resonator will lead to the decoherence of the two qubits coupled to it and the corresponding decrease in the entangling gate fidelity.
We also investigate the entangling gate fidelity as a function of the RX–resonator coupling strengthgRXand the transmon–resonator coupling strengthgtr.In Figs.4(d) and 4(e),the entangling gate fidelity increases rapidly with the increase of the coupling strengthgRXorgtruntil saturation and then decreases.This result can be explained by the fact that,on the one hand, an increase in the coupling strengthgRXorgtrleads to an increase in the effective coupling strengthJbetween the RX and transmon qubits,which shortens the entangling gate operation time and leads to a decrease in the error accumulation and an increase in the fidelity.On the other hand,when the coupling strength is further increased,the Purcell effect(κg2/?2)starts to play a role,and this decoherence effect will lead to a corresponding error as well as a reduction in fidelity.
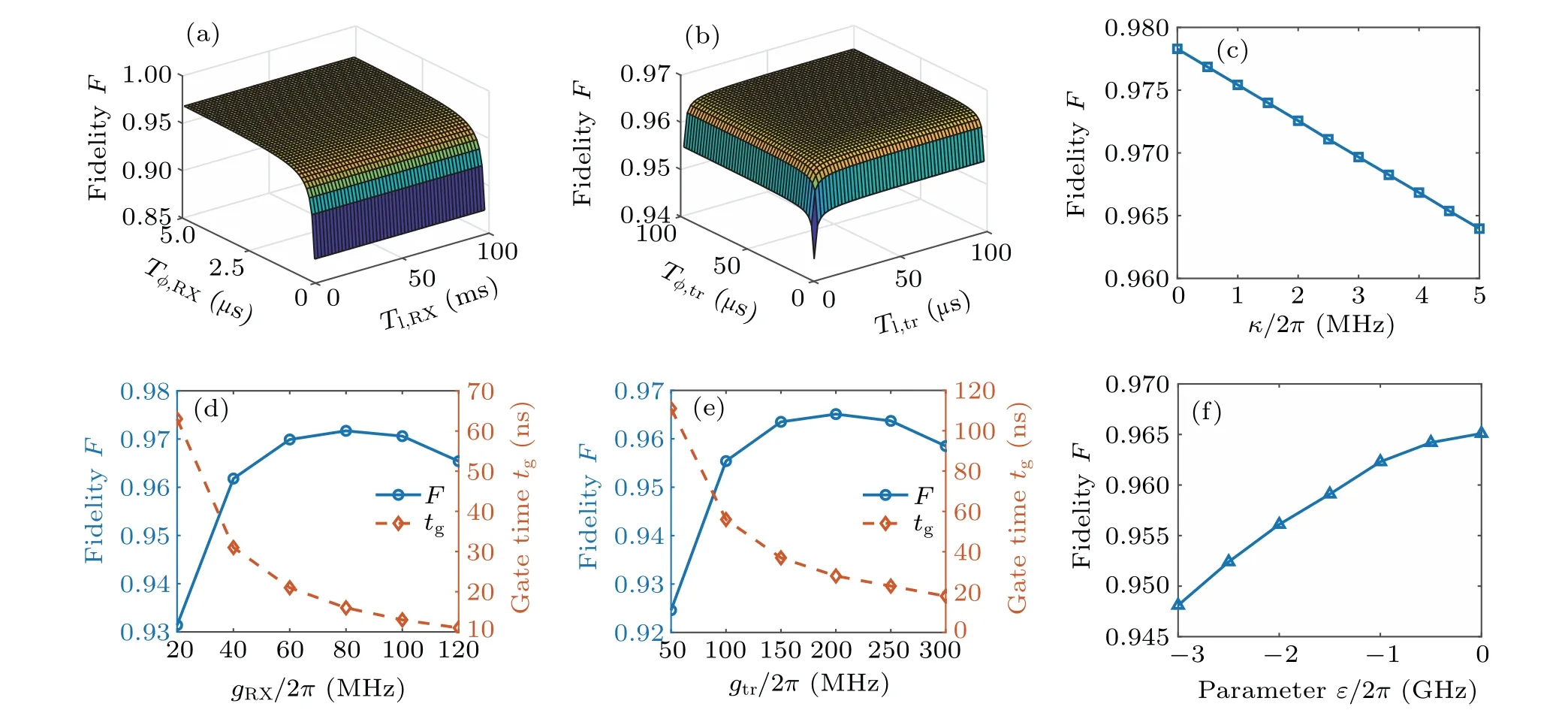
Fig.4.(a)Gate fidelity as a function of relaxation time Tl,RX and dephasing time Tφ,RX of RX qubit.(b)Gate fidelity as a function of relaxation time Tl,tr and dephasing time Tφ,tr of transmon qubit.(c)Gate fidelity as a function of photons decay rate κ.(d)Gate fidelity and gate time as a function of RX–resonator coupling strength gRX.(e)Gate fidelity and gate time as a function of transmon–resonator coupling strength gtr.(f)Gate fidelity as a function of asymmetry parameter ε of RX qubit.
Figure 4(f)shows that the entangling gate fidelity changes with the asymmetry parameterεof the RX qubits.The entangling gate fidelity increases from 94.8% to 96.5% whenεchanges from asymmetric to symmetric configuration.This result is consistent with that of the effective coupling strengthJbetween RX and transmon qubits in Fig.2(a).When the parameterεis changed to the symmetric configuration,the interaction strength between RX and transmon qubits becomes larger,resulting in a shorter entangling gate.Therefore,ε=0 can be considered as the sweet spot of the hybrid system where the entangling gate fidelity reaches its maximum.
6.Remote entanglement between two different qubits
We further demonstrate the generation of remote entanglement between RX and transmon qubits.Using two iSWAP gates and a single-qubit rotation gate, a controlled-NOT (CNOT) gate can be constructed, see Fig.5(a).The CNOT gate time can be estimated as 2tg~56 ns due to the short single-qubit gate time of the RX and transmon qubits compared to the iSWAP gate time.This fast two-qubit gate operation is the key to realizing the high-fidelity remote entanglement between the RX and transmon qubits.As shown in Fig.5(a),the scheme for generating distant entangled states consists of three steps: first, we prepare the initial states of the RX and transmon qubits with four different states,|0RX0tr〉,|1RX0tr〉,|0RX1tr〉, and|1RX1tr〉.Second, we apply a Hadamard gate on the RX qubit while keeping the transmon qubit unchanged.Finally, a CNOT gate is applied on the RX and transmon qubits.In this way, we generate the following remote entangled state:
In order to assess the quality of the remote entanglement between the RX and transmon qubits, we model the dynamics of the hybrid system using the master equation.Further,we reconstruct the density matrixρeof the RX and transmon qubits using quantum state tomography.Figures 5(b)–5(e)show the real part of the density matrixρefor the four initial states.We calculate the entanglement fidelityFe(ρ,ψ)=〈ψ|ρ|ψ〉 compared to the target Bell entangled state.The entanglement fidelity for the four cases ranges from 94.7%to 95.4%, which reaches the threshold for many network architecture-based quantum error correction protocols.[35,36]Compared to two-qubit entangling gates, both RX and transmon qubits have achieved high-fidelity single-qubit operations above 99.5%.[7,37]This implies that the single-qubit operations have a negligible effect on the generation of entangled states,while the two-qubit entangling gates are the main limiting factor for the fidelity of the entangled states.Thus, this scheme can generate high-fidelity entangled states between distant qubits and can be used for various quantum information processing in semiconductor–superconductor hybrid architectures.
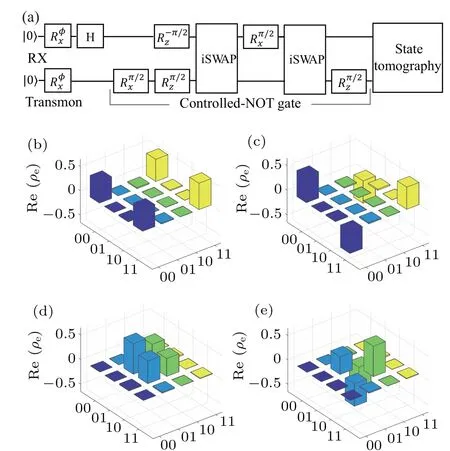
Fig.5.(a)Gate sequences for generating remote entanglement between RX and transmon qubits.(b)–(e)Quantum state tomography of the final density matrix ρe of the hybrid system for four initial cases.
7.Conclusions
In summary, we propose a scheme to generate highfidelity remote entanglement between RX and transmon qubits.Since the frequencies of the RX and transmon qubits can be adjusted, this hybrid system can operate in the dispersive regime,utilizing virtual microwave photons to realize interactions between different types of qubits.We find that the fidelity of entangling gates can reach a high value of 96.5%for a short time of 28 ns under the present experimental parameters.Furthermore, in combination with single-qubit gates,the scheme can be used to generate arbitrary remote entangled states.Such remote entanglement is an important quantum resource that can improve the connectivity and flexibility of hybrid architectures, making them more suitable for implementing quantum error-correction codes and fault-tolerant quantum computation.We also report that the decoherence process of the hybrid system limits the performance of the entanglement gates.The fidelity of entanglement gates can be further improved by increasing the qubit–resonator coupling strength and operating at the optimal points.This scheme provides a powerful solution for remote quantum information processing in hybrid architectures and can be extended to various solid-state quantum systems[38–40]in the future.
Appendix A:Spin structure of RX qubits
We consider three electrons located in a triple-quantum dot, with the RX qubit mainly operating in the symmetric charge configuration(1,1,1).There are eight spin states when considering the electrons with spin up or down.The logical states of the RX qubit are

By controlling the voltages on the TQD gate electrodes,we can control the parameter?and thus adjust the energy of the symmetric configuration with respect to the asymmetric ones.In this way, there are a total of four relevant states for the RX qubit:|0〉,|1〉,|2〉,|3〉.The tunnel couplingtl(tr)between the left(right)quantum dot and the middle quantum dot hybridizes these states,which leads to the formation of the two RX qubit states|0RX〉and|1RX〉.
Appendix B:Effect of exchange interactions
For a triple-quantum dot, the tunneling effects between adjacent quantum dots give rise to two exchange interactions,Jlbetween the pair of electrons in the left and middle dots,andJrbetween the pair of electrons in the middle and right dots.In the basis of{|0〉,|1〉,|2〉,|3〉},the Hamiltonian of TQD can be described as
First we study the effect of exchange interactions by analytic methods.In the limit of|?±ε|?tl(tr),the RX qubit is defined in the symmetric charge configuration(1,1,1),which is spanned by the states|0RX〉?|0〉and|1RX〉?|1〉.These two states are obtained by elimination of the higher-energy threeelectron states in the asymmetric charge configurations(2,0,1)and (1,0,2) using a Schrieffer–Wolff transformation.The resulting effective Hamiltonian in this subspace is given by

We then use numerical methods to study the effect of exchange interactions.For this purpose, we directly calculate the energy level structure of the TQD HamiltonianHTQD.As shown in Fig.1(b), the RX qubit state is defined as the two lowest energy levels|0RX〉 and|1RX〉.We note that in the regime nearε=0,the energy levels change little with the control parameterε,Thus,as a sweet spot,qubits at this working pointε=0 are weakly coupled to charge noise.
Appendix C: Coupling between spin qubits and resonators
In the basis of{|0〉,|1〉,|2〉,|3〉},a triple-quantum dot system can be described by a four-level HamiltonianHTQD.Then,we diagonalize the above Hamiltonian to encode the RX spin qubits with the two lowest states|0RX〉 and|1RX〉.The RX qubit states can be expressed as a linear combination of the states|0〉,|1〉,|2〉,|3〉,denoted as

wheregchis the charge–resonator coupling strength, (a+a?)is the electric field of the resonator, and|2〉 is the polarized charge state of the quantum dot system to which it is coupled.Then we convert the above TQD–resonator interaction HamiltonianHTQD,Sqto the RX qubit state space.In the basis of{|0RX〉,|1RX〉},the corresponding Hamiltonian is given by

Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos.11974336 and 12304401), the National Key R&D Program of China (Grant No.2017YFA0304100), the Key Project of Natural Science Research in Universities of Anhui Province (Grant No.KJ2021A1107), and the Scientific Research Foundation of Suzhou University (Grant Nos.2020BS006 and 2021XJPT18).
- Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution

