Logics of Non-actual Possible Worlds*
Jie Fan
Abstract. In Jia Chen(2020),a logic of strong possibility and weak necessity,which we call‘logic of non-actual possible worlds’ here,is proposed and axiomatized over various frames.However,the completeness proof therein is quite complicated,which involves the use of copies of maximal consistent sets in the construction of the canonical model,among other considerations.In this paper,we demonstrate that the completeness of some systems thereof can be reduced to those of the familiar systems in the literature via translations,which builds a bridge among these systems.We also explore the frame definability of such a logic.
1 Introduction
Standard modal logic concerns about notions of necessity and possibility.Intuitively,a proposition is possible,if it is true at some accessible possible world;it is necessary,if it is true at all accessible possible worlds.For standard modal logic,refer to any textbook on modal logic,e.g.[1].Here possible worlds include not only the actual(i.e.real)world,but also those non-actual ones.The existence of non-actual possible worlds is supported by modal realists,represented by David Lewis(e.g.[8]).
The notion of non-actual possible worlds is related to the actualism vs.possibilism dispute.According to actualism,everything that there is,everything that has being in any sense,is actual,which states in terms of possible worlds that everything that exists in any world exists in the actual world.By contrast,possibilism thinks that there are things that exist in other possible worlds but fail to exist in the actual world,which are called ‘mere possibilia’.Non-actual possible worlds are prime examples of such mere possibilia.([10])
The notion of non-actual possible worlds is also related to counterfactual reasoning and imagination.For instance,as known,Donald Trump was not elected as the 46th U.S.president.But we can imagine what would happen if Donald Trump had been elected as the 46th U.S.president.Non-actual possible worlds are indispensable in such imagination and counterfactual reasoning.Moreover,although the world we are living in,that is,the real world,is also a possible world,in some cases,however,we are more interested in those non-actual possible worlds than the actual one.1For instance,the worlds in science fiction and film are usually non-actual possible worlds,and in deontic logic,we usually hope to find deontically ideal worlds,which are again non-actual possible worlds.
In this paper,we investigate a logic of non-actual possible worlds,which dates back to[6],under the name of‘a(chǎn) logic of strong possibility and weak necessity’.2If it is proper to call the standard modal logic‘the logic of possible worlds’,then we may also call the logic of strong possibility and weak necessity‘the logic of non-actual possible worlds’,in which we are mainly concerned with those non-actual possible worlds.Note that the term‘weak necessity’is also used in the deontic setting,see for instance[13].Partly because of this,we prefer to use the term‘the logic of non-actual possible worlds’rather than‘the logic of strong possibility and weak necessity’.Intuitively,a proposition is strongly possible,if it is true at some accessible non-actual possible world;it is weakly necessary,if it is true at all accessible non-actual possible worlds.The logic is axiomatized over various classes of frames.However,the completeness proofs via a variant of the usual canonical model construction thereof are quite complicated,which involves the use of copies of maximal consistent sets,among other considerations.
Observing the proof systems of the logic of non-actual possible worlds and the ?-based normal modal logics,we can see the similarities in form between their minimal logics (denoted ?K and K,respectively) and symmetric logics(denoted ?B and B,respectively).This inspires us that we may use a method to show the completeness of?K and ?B rather than canonical model constructions.The method in question is the reduction via translations.In details,by finding suitable translation functions,we can obtain the axiom schemas and inference rules of ?K from K and ?B from B,and vice versa.Another observation is that,although the semantics of ?and ?are different in general,they are the same (i.e.equivalent) on irreflexive models.Based on the two observations,we can reduce the determination results (that is,soundness and completeness)of ?K and ?B to those of K and B,respectively.This much simplifies the completeness proof of ?K and ?B.
Our logic is also related to the modal logic for elsewhere ([7]),which is also called the logic of somewhere else([14,p.69]),the modal logic of inequality([11]),and the modal logic of other worlds([4]).This logic is axiomatized over the class of all frames 〈W,R〉 in which for allx,y∈W,xRyif and only ifx≠y(in short,Ris nonidentity) in [12],and a more elegant axiomatization,denotedKAB,is given in [7].When it comes to form,the symmetric and transitive logic (denoted ?B4 below)has the same axioms and inference rules asKAB.Moreover,their semantics are the same on the models which we call ‘conversely irreflexive models’.As we shall show,the determination result of the former system can be reduced to that of the latter.
As a matter of fact,the semantics of everywhere-else and somewhere-else operators can be thought of as special instances of weak necessity and strong possibility operators,respectively,when the accessibility relation is universal.
The remainder of the paper is organized as follows.Sec.2 introduces the syntax and semantics of the logic L(?)of non-actual possible worlds and some related logics.Sec.3 reviews axiomatizations of the modal logic for elsewhere and L(?).Sec.4 investigates its frame definability.Sec.5 presents several translation functions,which either reduce the determination results of some axiomatizations of L(?)to those in the literature,or help us find a simpler axiomatization of L(?)over transitive frames.We conclude with some future work in Sec.6.
2 Syntax and semantics
Throughout the paper,we fix P to be a nonempty set of propositional variables and letp∈P.We first define a large language,which has the language of the logic of non-actual possible worlds as fragments.
Definition 1(Languages).The language L(?,?,) is defined recursively as follows:
With the sole modal construct ?φ,we obtain the language L(?)ofthe logic of nonactual possible worlds,aliasthe logic of strong possibility and weak necessity;with the sole modal construct ?φ,we obtain the language L(?)of standard modal logic;with the sole modal constructφ,we obtain the language L()of the logic of elsewhere.
Intuitively,?φ,?φ,andφare read,respectively,“it isweakly necessarythatφ”,“it is necessary thatφ”,and “it is the case thatφeverywhere else”.Other connectives are defined as usual.In particular,?φ,◇φ,and Dφare read “it is strongly possible thatφ”,“it is possible thatφ”,and “it is the case thatφsomewhere else”,and abbreviate???φ,???φ,and??φrespectively.We will mainly focus on the logic L(?)in the sequel.
Given a model M=〈W,R,V〉and a worldw∈W,the semantics of L(?,?,)is defined inductively as follows:
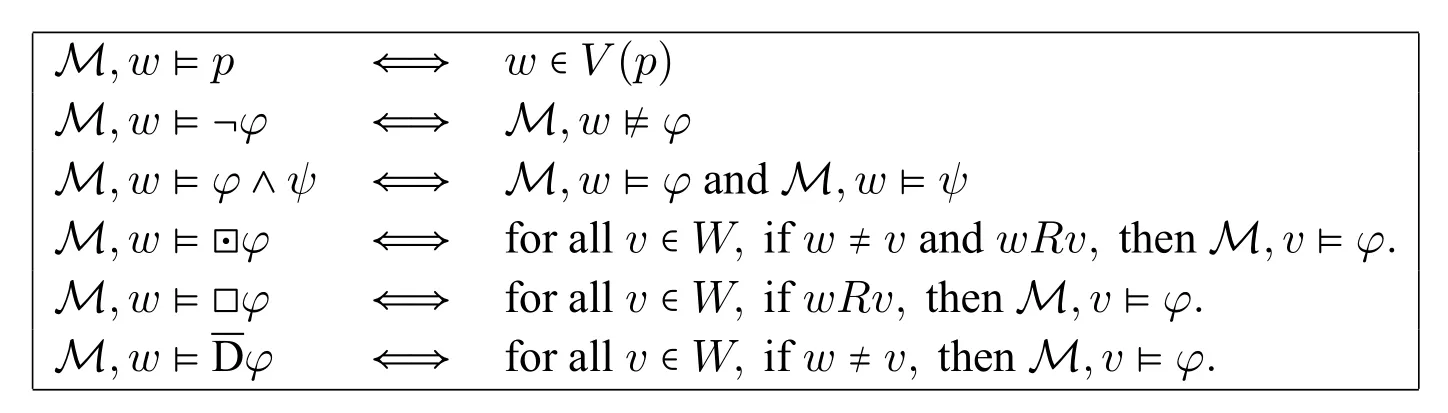
Notions of truth,model validity,frame validity and semantic consequence are defined as usual.
Observe that the semantics of ?can be seen as a ‘combination’ of those of ?and,in the sense that the antecedent of the interpretation of ?φ(namely ‘w≠vandwRv’),is a conjunction of those of the interpretation of ?φandφ.Besides,the semantics ofcan be seen as a special case of ?when the accessibility relationRis universal.
One may see that the semantics of ?and ?are different in general.However,they are the same on the models in which the following condition are satisfied:
It should be easy to verify that(Irref)amounts to saying that the models are irreflexive:
Also,even though the semantics of ?andare different in general,they are the same on the models that have the following property:
As easily seen,(Ci)is just the converse of(Irref).For this reason,we use the name(Ci),to stand for C(onverse)i(rreflexivity).Both(Irref)and(Ci)play important roles in our paper.
One may easily compute the semantics of the defined operators as follows.
M,w?φthere existsvsuch thatw≠vandwRvand M,v?φ.
M,w?◇φthere existsvsuch thatwRvand M,v?φ.
M,w?Dφthere existsvsuch thatw≠vand M,v?φ.
Note that ??φ→?φ.That is why ?is called the operator of weak necessity.This follows by the monotony of ?that ??nφ→?nφfor alln∈N.It may be worth remarking that over reflexive models,?is definable in terms of ?,as ?φ=df?φ∧φ.This will guide us to propose a translation between L(?)and L(?),and then a transitive axiom in the latter language.
3 Existing results on axiomatizations of L()and L(?)
3.1 Existing results on axiomatizations of L()
The minimal normal logic of L(),denoted SWB+A5 in[14],orKABin[7],orDL-in[11],or KB4′in[4],consists of the following axioms and inference rules.Here we follow[7]and call the systemKAB.
It is shown in[7]thatKABis determined by(that is,sound and complete w.r.t.)not only the class of all frames under the semantics of L(),but also two extra classes of frames(see Thm.1 below).Here the more unusual condition ofaliotransitivitycan be expressed in first-order logic as
Theorem 1.([7])
·KAB is sound and strongly complete with respect to the class of aliotransitive and symmetric frames?
·KAB is sound and strongly complete with respect to the class of(Ci)-frames?
·KAB is sound and strongly complete with respect to the class of frames where the accessibility relation is nonidentity.
In what follows,we will make use of the determination result ofKABby the class of(Ci)-frames to obtain that of ?B4 below by the class of B4-frames,through a method of reduction via translations.
3.2 Existing results on axiomatizations of L(?)
Recall that the minimal logic of L(?),denoted ?K,which consists of the following axioms and inference rules,is given in[6,p.62].
It is easy to see that ?K is normal,thus it is monotone,namely,if ?φ→ψ,then??φ→?ψ.
Theorem 2.([6,Thm.4])?Kis sound and strongly complete with respect to the classKof all frames,the classDof all serial frames,the classTof all reflexive frames.In symbols,for allX ∈{K,D,T},for allΓ ∪{φ}?L(?),we have
It is then extended to other systems and various soundness and strong completeness results obtain.
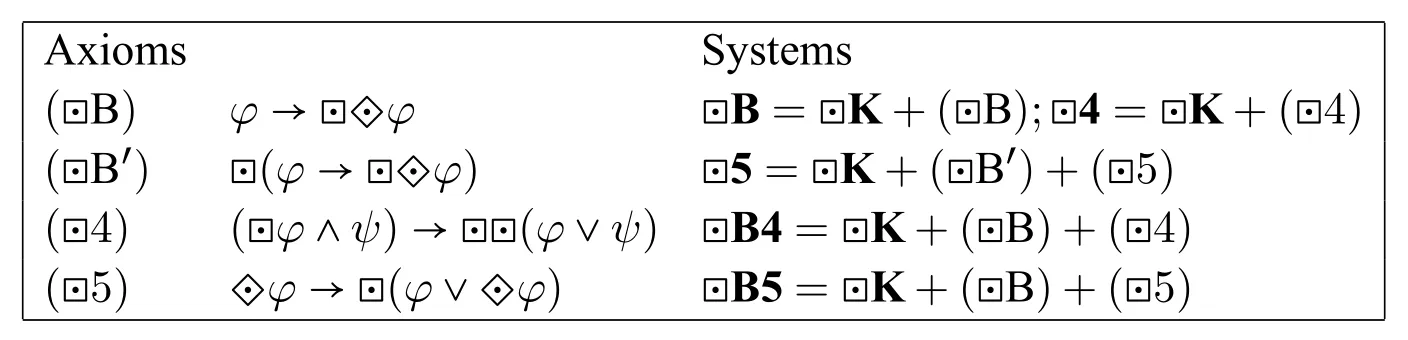
Theorem 3.([6,Thm.5,Thm.6])
(1) ?Bis sound and strongly complete with respect to the class ofB-frames,to the class ofDB-frames,and to the class ofT B-frames.
(2) ?4is sound and strongly complete with respect to the class of4-frames,to the class ofD4-frames,and to the class ofS4-frames.
(3) ?5is sound and strongly complete with respect to the class of5-frames,and to the class ofD5-frames.
(4) ?B4(and its equivalent system?B5)is sound and strongly complete with respect to the class ofB4-frames(equivalently,the class ofB5-frames)and to the class ofS5-frames.3Note that it is claimed without proof in[6]that ?B4 and ?B5 are equivalent.In what follows,we will give a proof.
However,the proof of the strong completeness of ?K(and thus its extensions)in [6]is quite complicated,needing,among other things,to make use of copies of maximal consistent sets in the construction of the canonical model.For the details,we refer to[6]or Appendix below.
Note that in terms of the form,the axioms and inference rules of the system?K are similar to those of the minimal normal modal logic K,which consists of the following axioms and inference rules:
Also,when it comes to the form,the axioms and inference rules of the system ?B is similar to those of the normal modal logic B,which is the smallest normal extension of K with an extra axiomφ→?◇φ,denoted ?B.
In what follows,we will give a simpler proof for the completeness of ?K and ?B,by reducing the soundness and strong completeness of the two systems,respectively,to those of K and B.
Moreover,we can see other ?-axioms arenotsimilar in form to their ?-counterparts that are used to provide completeness of normal modal logics.We will explain why this is the case,which will in turn explain that the completeness of the other four systems,namely ?4,?5,?B4 and ?B5,cannot be reduced to those of their corresponding?-systems via the translation function used in the case of ?K and ?B.
Furthermore,although the axiom (?4) in the proof system ?B4 is not similar in form to its counterpart in ?-based normal modal logics,one of its simpler equivalences(denoted(?4′)below)is indeed similar in form to the axiom(D4)in the proof systemKABintroduced above.By giving two translation functions,among some semantic considerations,we will finally demonstrate in Sec.5.2 that the soundness and completeness of ?B4 can be reduced to those ofKAB.
4 Irreflexive reduction
This section proposes a notion called ‘irreflexive reduction’.This notion will play a crucial role in the frame definability,and more importantly,in the completeness of the proof systems ?K and ?B of L(?)below.
Intuitively,the irreflexive reduction of a frame is obtained from the original frame by deleting all reflexive arrows.It is easy to see that every frame has a unique irreflexive reduction.4The notion of irreflexive reduction differs from the notion of mirror reduction in [9],in that the irreflexive reduction is also a mirror reduction,but not vice versa.Every frame may have many mirror reductions,but has only one irreflexive reduction.
Definition 2(Irreflexive reduction).Let F=〈W,R〉 be a frame.Frame F-T=〈W,R-T〉is said to theirreflexive reductionof F,if
Moreover,say that M-T=〈F-T,V〉is theirreflexive reductionof M=〈F,V〉,if F-Tis the irreflexive reduction of F.We say that a class of frames C isclosed under irreflexivization,if F ∈C implies F-T∈C.
The satisfiability and frame validity of L(?)-formulas are invariant under the notion of irreflexive reduction.We omit the proof details due to space limitation.
Proposition 1.LetF-T=〈W,R-T〉be the irreflexive reduction ofF=〈W,R〉,and letM=〈F,V〉andM-T=〈F-T,V〉.Then
(a)For all w∈W,for all φ∈L(?),we have
(b)For all φ∈L(?),we have
It is claimed without proof in[6,p.65]that the property of symmetry is definable in L(?),byp→??p,but other familiar frame properties,such as seriality,reflexivity,transitivity,Euclideanness,are undefinable in this language.Here we give a proof for the undefinability results with the notion of irreflexive reduction.
A frame propertyPis said to be definable in a language,if there exists a set of formulas Γ in this lanaguage such that for all frames F,we have F ?Γ iff F has the propertyP.We write simply F ?φif Γ is a singleton{φ}.
Theorem 4.Seriality,reflexivity,transitivity,Euclideanness,and convergence are all not definable inL(?).
Proof.Consider the following frames:
The following results will be used in the completeness proof.Given a class of frames C,define C-T={F-T: F ∈C},where F-Tis the irreflexive reduction of F.In other words,C-Tis the set of the irreflexive reduction of each frame in C.
Lemma 1.LetCandC′be two classes of frames.IfC-T=C′-T,then for all?!葅φ}?L(?),we have
Proof.By Prop.1(a),we can show that Γ ?Cφiff Γ ?C-T φ,and Γ ?C′φiff Γ ?C′-T φ.Since C-T=C′-T,we conclude that Γ ?Cφiff Γ ?C′φ.?
Given any class of frames X,one may check that if T ?X,then X-T=T-T,and if S5 ?X ?B4,then B4-T=X-T=S5-T.Then by Lemma 1,we immediately have the following special semantic properties of L(?).
Proposition 2.LetΓ ∪{φ}?L(?).
(1)Γ ?XφΓ ?Tφ forT ?X?
(2)Γ ?B4φΓ ?XφΓ ?S5φ forS5 ?X ?B4.
We close this section with an important result,which says that L(?)is insensitive to reflexivity,that is,adding or deleting reflexive arrows does not change the validity of L(?)-formulas in a given frame(satisfiability,for that matter).
Proposition 3.LetM1=〈W,R1,V〉andM2=〈W,R2,V〉be models such that R1and R2only differ in pairs of reflexive arrows.Then for all w∈W,for all φ∈L(?),we have
Proof.Note that M1and M2must have the common irreflexive reduction.Then use Prop.1(a).?
5 Reducing completeness via translations
In this section,we reduce some proof systems in L(?)to the more familiar ones in the literature,by proposing several translation functions.Given any translation functionfand any set of formulas Γ,we define Γf={φf∣φ∈Γ}.
5.1 Reducing completeness of ?K and ?B
In this part,we reduce the(soundness and)strong completeness of the unfamiliar proof systems ?K and ?B to those of the familiar ones K and B,respectively,by giving a pair of translation functions,namely ?-translation(?)?and ?-translation(?)?.The strategy can be summed up as follows.For all Γ ∪{φ}?L(?),
In what follows,we will show the case for ?K in detail.The proof for ?B is analogous.
Definition 3(?-translation,?-translation).Define the ?-translation(?)?:L(?)→L(?)and the ?-translation(?)?:L(?)→L(?)as follows:
One may easily see that both (?)?and (?)?aredefinitionaltranslations,since they are variable-fixed and compositional.5As for the notion of definitional translations,we refer to[5,p.265].Intuitively,the ?-translation replaces all occurrences of ?in every L(?)-formula with ?,and the ?-translation replaces all occurrences of ?in every L(?)-formula with ?.It is straightforward to show by induction that (φ?)?=φfor allφ∈L(?) and (ψ?)?=ψfor allψ∈L(?).In general,(Γ?)?=Γ for all Γ ?L(?)and(Σ?)?=Σ for all Σ ?L(?).
The following result is an immediate consequence of the purely notational difference between the axiomatizations K and ?K.
Lemma 2.For allΓ ∪{φ}?L(?),Γ ??Kφ iffΓ??Kφ?.
This completes the step(1)in the above strategy.The step(2)is immediate by the soundness and strong completeness of K.It remains only to show the step (3).For this,we need some preparation.
Recall that we remarked that the semantics of ?and ?are the same on the irreflexive models.Here is a formal exposition,which can be shown by induction on L(?)-formulas.
Proposition 4.For all irreflexive modelsM,for all worlds w inM,for all φ∈L(?),we have
Recall from Def.2 that M-Tis the irreflexive reduction of M.The following result is a direct consequence of Prop.1(a),Prop.4 and the fact that M-Tis irreflexive.
Corollary 1.For all modelsM,for all worlds w inM,for all φ∈L(?),we have
Consequently,for allΓ ?L(?),M,w?ΓiffM-T,w?Γ?.
Lemma 3.For allΓ ∪{φ}?L(?),we have
Proof.Suppose that ΓKφ.Then there exists a model M and a worldwsuch that M,w?Γ and M,wφ.By Coro.1,M-T,w?Γ?and M-T,wφ?.Therefore,Γ?Kφ?.
Now assume that Γ?Kφ?.Then there exists M andwsuch that M,w?Γ?and M,wφ?.Since Γ?∪{φ?} ?L(?),by a well-known result6The result is as follows.For each model M and w in M,there is an irreflexive model M′ and w′in M′ such that for each φ ∈L(?),That is,every model can be transformed into a pointwise-equivalent irreflexive model.in the modal logic literature (see e.g.[2,p.48]),there must be an irreflexive model M′andw′such that M′,w′?Γ?and M′,w′φ?.Note that M′=(M′)-T.This means that(M′)-T,w′?Γ?and(M′)-T,w′φ?.By Coro.1 again,we infer that M′,w′?Γ and M′,w′φ,and therefore ΓKφ.?
With the above results in hand,we obtain the soundness and strong completeness of ?K.As a matter of fact,we can show the following general result.
Theorem 5.LetT ?X ?K.Then?Kis sound and strongly complete with respect to the class ofX-frames.That is,for allΓ ∪{φ}?L(?),we have that: Γ ??KφΓ ?Xφ.
Proof.Let Γ ∪{φ}?L(?).We have the following equivalences:
where the first equivalence follows from Lemma 2,the second from the soundness and strong completeness of K,the third from Lemma 3,and the last two equivalences follow from Prop.2(1).?
Corollary 2.[6,Thm.4]?Kis sound and strongly complete with respect to the classKof all frames,to the classDof all serial frames,and to the classTof all reflexive frames.
As with the reduction of the sound and strong completeness of ?K to those of K,we can also reduce the soundness and strong completeness of ?B to those of B.Note that[2,p.48]also tells us that every symmetric model can be transformed into a pointwise-equivalent irreflexive symmetric model,thus we can show a similar result to Lemma 3.
Theorem 6.[6,Thm.5(1)]?Bis sound and strongly complete with respect to the class ofB-frames,the class ofDB-frames,and also the class ofT B-frames.
Similarly,the soundness and completeness of the bimodal logics of L(?,?)7The language L(?,?)is the extension of L(?)with the modal construct ?φ.,namely K+and KB+in[6],can be reduced to those of normal modal logics K and B,respectively,by translating ?φto ?φ.We omit the proof details due to space limitation.
We have seen from Sec.3 that the axioms(?K)and(?B)are similar in form to their counterparts in ?-based normal modal logics,that is,(?K) and (?B),respectively.However,this is not the case for other axioms.One may ask why it is so.In what follows,we provide an explanation for this phenomenon.
Proposition 5.LetCbe a class of frames.If(i)Cis closed under irreflexivization,then(ii)for all φ∈L(?),ifC ?φ,thenC ?φ?.
Proof.Suppose that (i) holds,to show that (ii) holds.For this,letφ∈L(?) and assume that C ?φ?,it suffices to prove that C ?φ.
By assumption,there is a C-model M=〈W,R,V〉andw∈Wsuch that M,w?φ?.By Coro.1 andφ?∈L(?),M-T,w?(φ?)?,that is,M-T,w?φ.Note that M-Tis also a C-model,which follows from the fact that M is a C-model and (i).Thus C ?φ.?
Since ?K and ?B are,respectively,valid on the class of all frames and the class of symmetric frames,and both frame classes are closed under irreflexivization,?K and ?B are valid with respect to the corresponding classes of frames.
Corollary 3.
(1) ?(φ→ψ)→(?φ→?ψ)is valid on the class of all frames.
(2)φ→??φ is valid on the class of symmetric frames.
We have seen from Prop.5 that(i)is asufficientcondition of(ii).One may then naturally ask whether(i)is also anecessarycondition of(ii).In general,the answer would be negative.
Proposition 6.LetCbe the class of all frames which has at least one reflexive point.Then(i)of Prop.5 fails,but(ii)of Prop.5 holds.
Proof.One may check that C is not closed under irreflexivization,thus(i)of Prop.5 fails.In what follows,we show that for allφ∈L(?),(1)C ?φimplies ?φ,(2)?φimplies ?φ?,and(3)?φ?implies C ?φ?.This entails that C ?φimplies C ?φ?,namely(ii)of Prop.5.(3)is straightforward.It remains only to show(1)and(2).
For (1): suppose that ?φ,then ?φis satisfiable.By finite model property of L(?),there exists a finite model,say M,andw∈M,such that M,w??φ.Let M′=〈W′,R′,V′〉 such thatW′={s} wheres?M (since M is finite,suchsmust exist),R′={(s,s)}.Now consider the disjoint union of M and M′,say M′′.Since M′′contains the reflexive points,its underlying frame belongs to C.Moreover,as modal satisfaction is invariant under disjoint unions(see e.g.[1]),we have M′′,w??φ,and therefore C ?φ.
For(2): assume that ?φ?,then there is a model N andusuch that N,u?φ?.Sinceφ?∈L(?),by Coro.1,N-T,u?(φ?)?.We have shown previously that(φ?)?=φ.Thus N-T,u?φ,and therefore ?φ,as desired.?
Despite this,below we shall show that the converse of Prop.5 indeed holds when C is the class of serial frames,the class of reflexive frames,the class of transitive frames,or the class of Euclidean frames.Note thatnoneof such class of frames is closed under irreflexivization,which can be seen from the figures in the proof of Thm.4.
Proposition 7.LetCbe the class ofD-frames,the class ofT-frames,the class of4-frames,or the class of5-frames.Then there is a φ∈L(?)such thatC ?φ butC ?φ?.
Proof.If C is the class of D-frames,we letφ=?p→◇p.On one hand,it is well known that C ?φ.On the other hand,C ?φ?,whereφ?=?p→?p.To see this,consider a model,say M1,which contains only a single world that is reflexive,sayw1(where the valuation is inessential).We can check that M1is serial and M1,w1??p∧??p.
If C is the class of T-frames,we letφ=?p→p.It is well known that C ?φ.However,C ?φ?,whereφ?=?p→p.To see this,consider a model,say M2,which consists of a single reflexive world,sayw2,falsifyingp.It is easy to see that M2is reflexive.Moreover,one can show that M2,w2??p∧?p.
If C is the class of the class of 4-frames,we letφ=?p→??p.On one hand,C ?φ.On the other hand,C ?φ?,whereφ?=?p→??p.To see this,consider a model,say M3,which consists of two worldsw3andvsuch that the accessibility relation is universal andpis only true atv.One may check that M3is transitive and M3,w3??p∧???p.
If C is the class of 5-frames,we letφ=◇p→?◇p.On one hand,we have C ?φ.On the other hand,C ?φ?,whereφ?=?p→??p.To see this,consider a model M4,which consists of two worldsw4andusuch thatw4accesses touanduaccesses to itself and there are no other accesses,andpis only true atu.It is clear that M4is Euclidean.Moreover,one may verify that M4,w4??p∧???p.?
5.2 Reducing completeness of ?B4
We now reduce the soundness and strong completeness of ?B4 to those ofKAB.The strategy is as before,except for an additional step: for all Γ ∪{φ}?L(?),
where(?)tis defined below.
To obtain the desired system ?B4′,we define the following translation function.
Definition 4.Define the ★-translation(?)★:L(?)→L(?)as follows:
Recall that the transitivity axiom in L(?) is ?φ→??φ.Using the above ★-translation,we obtain the following formula:
In the system ?K,this formula can be simplified to the following equivalent one,denoted(?4′):
Define ?B4′=?B+(?4′).We choose(?4′)instead of(?4)(namely,?φ∧ψ→??(φ∨ψ))in the system ?B4,partly because this axiom is simpler than the latter,and partly because it is more convenient in showing that ?B4 is equivalent to ?B5;more importantly,it is similar in form to the axiom(D4)inKAB,which is useful in the completeness proof of ?B4.
Proposition 8.?4and?4′are interderivable in?K.8This is claimed without proof in[6,p.65].
Proof.Firstly,(?4)(?4′): letψin(?4)beφ.Then apply the ruletwice,which is derivable from the axiom ?K and the inference rule ?N.
Secondly,(?4′)(?4): suppose that (?4′).We have the following proof sequences in ?K.
Corollary 4.?4=?K+(?4′)??B4=?B4′.Therefore,Γ ??B4φΓ ??B4′φ.
We have thus finished the step(*).To complete the step(**),we introduce a pair of translations.
Definition 5.Define the translation (?)t: L(?) →L() and the translation (?)s:L()→L(?)as follows.
Again,both(?)tand(?)saredefinitionaltranslations.Intuitively,thet-translation replaces all occurrences of ?in every L(?)-formula with,and thes-translation replaces all occurrences ofin every L()-formula with ?.Moreover,(φt)s=φfor eachφ∈L(?),and(φs)t=φfor eachφ∈L().This also extends to the set of formulas;that is,(Γt)s=Γ for each Γ ?L(?),and(Γs)t=Γ for each Γ ?L().
As with Lemma 2,we can show the following.
Lemma 4.LetΓ ∪{φ}?L(?).ThenΓ ??B4′φ iffΓt?KAB φt.
It remains only to show the step(****).For this,we need some preparations.First,as mentioned before,the semantics of ?andare the same over Ci-models.Here is a formal exposition,which can be shown by induction on L()-formulas.
Proposition 9.For all Ci-modelM=〈W,R,V〉and w∈W,for all φ∈L(),wehave
Proposition 10.For each Ci-modelM=〈W,R,V〉and w∈W,there exists someB4-modelM′such that for all φ∈L(D),
Proof.We take the reflexive closure of M,denoted M+T.One may easily show that M+Tis transitive and symmetric.Moreover,by Prop.9,M,w?φiff M,w?φs.Note thatφs∈L(?).By Prop.3,M,w?φsiff M+T,w?φs.Therefore,
M,w?φiff M+T,w?φs.?
The following result plays a crucial role in the completeness proof via reduction below.
Proposition 11.For eachB4-modelN=〈W,R,V〉and w∈W,there exists some Ci-modelN′such that for all φ∈L(?),
Proof.We take the submodel of N generated byw,denoted Nw=〈U,R′,V′〉.We can show that L(?)-formulas are invariant under the generated submodels,as in the case of the standard modal logic.Also,the properties of symmetry and transitivity are preserved under generated submodels,thus Nwis also a B4-model.Now we show that Nwis a Ci-model,which is divided into two steps:9The proofs of the two steps are shown as in[7,p.185],where the proofs are for the canonical model,rather than an arbitrary B4-model,though.
(a) for allm∈N,for allx∈U,ifw≠xandw(R′)mx,thenwR′x.
(b) for allx,y∈U,ifx≠y,thenxR′y.
The proof for(a)is by induction onm∈N.The casem=0 holds vacuously.Suppose,as induction hypothesis,that(a)holds for some fixedm,we show(a)also holds form+1.For this,we assume thatw≠xandw(R′)m+1x.Then there existsu∈Usuch thatw(R′)muanduR′x.Ifw=u,then it is clear thatwR′x.Otherwise,that is,w≠u,then by induction hypothesis,it follows thatwR′u.Now by transitivity ofR′andwR′uanduR′x,we obtainwR′x.
The proof for(b)is as follows.Suppose thatx≠yfor allx,y∈U.Then there arem,n∈N such thatw(R′)mxandw(R′)ny.
Ifw=x,thenw≠y,by(a),it follows thatwR′y,and thusxR′y.
Ifw=y,thenw≠x,by(a)again,wR′x,that is,yR′x.Now by symmetry ofR′,we inferxR′y.
Ifw≠xandw≠y,then by(a)again,we obtainwR′xandwR′y.SinceR′is symmetric and transitive,R′is Euclidean,thusxR′y.
So far we have shown that Nwis a Ci-model.It suffices to show that Nw,w?φiff Nw,w?φtfor allφ∈L(?).The proof proceeds with induction onφ.The nontrivial case is ?φ.This follows directly from the previous remark that the semantics of ?andare the same on the Ci-models.?
Lemma 5.LetΓ ∪{φ}?L(?).ThenΓ ?B4φ iffΓt?Ci φt.
Proof.‘Only if’: suppose that Γt?Ciφt.Then there is a Ci-model M andwin M such that M,w?Γtand M,w?φt.By Prop.10,there exists a B4-model M′such that M′,w?(Γt)sand M′,w?(φt)s.That is,M′,w?Γ and M′,w?φ.Therefore,Γ ?B4φ.
‘If’: assume that Γ ?B4φ.Then there exists a B4-model N andwin N such that N,w?Γ and N,w?φ.Now by Prop.11,there exists some Ci-model N′such that N′,w?Γtand N′,w?Γt.Therefore,Γt?Ciφt.?
With the above results in mind,we can obtain the soundness and strong completeness of ?B4.As a matter of fact,we can show the following general result.
Theorem 7.LetS5 ?X ?B4.Then?B4is sound and strongly complete with respect to the class ofX-frames.That is,for anyΓ ∪{φ}?L(?),Γ ??B4φ iffΓ ?Xφ.
Proof.We have the following proof equivalences:
where the first equivalence follows from Coro.4,the second from Lemma 4,the third from Thm.1,the fourth from Lemma 5,and the last two follow from Prop.2(2).?
Corollary 5.?B4is sound and strongly complete with respect to the class ofXframes,whereX ∈{B4,B4D,S5}.
Theorem 8.?B5is sound and strongly complete with respect to the class ofXframes,whereS5 ?X ?B4.
Proof.By Coro.4 and Thm.7,it suffices to show that ?B4′=?B5.
We first show that ?5 is provable in ?B4′.We have the following proof sequence in ?B4′,where(?4′)dmeans the dual formula of ?4′.
Next,we show that ?4′is provable in ?B5.We have the following proof sequence in ?B5,where(?5)dmeans the dual formula of ?5.
It is worth remarking that from axiom 5(namely,◇φ→?◇φ),the ★-translation in Def.4 gives us the following axiom,denoted ?5′:
It should be not hard to verify that ?B+?5′=?B5.
6 Conclusion and future work
Our contribution is mainly technical.We investigate the frame definability of the logic of non-actual possible worlds L(?).Most importantly,by defining suitable translation functions,we reduced the determination results of ?K,?B,?B4 to those of K,B,KAB,respectively.For us,this method,namely reduction-via-translations,is simpler than the direct proof method of using copies of maximal consistent sets in[6].The hardest of this method lies in the reduction of the semantic consequence relation.This establishes some metaproperties of L(?),for instance,decidability.This also build a bridge between L(?)and L(?),and L(?)and L().We also explained why other ?-axioms cannot be obtained from the corresponding ?-axioms by using ?-translation.We can also extend the axiomatization results to the dynamic cases.
Coming back to Prop.3,we can see that L(?)is insensitive to reflexivity,that is,adding or deleting reflexive arrows does not change the validity (satisfiability,for that matter) of ?-formulas in a given frame.This is similar to the case for the logic of essence and accident L(○)([9]).Due to this crucial observation,similar to L(○)in[3],one may give a generalized completeness and soundness result for L(?).Besides,one can investigate if the soundness and strong completeness ofKABin[7]can be reduced to some system in L(?)by a certain translation.Moreover,one may explore the applications of L(?) in counterfactual reasoning and imagination.We leave this for future work.
7 Appendix
This appendix is intended to describe the completeness proof of ?K.
Due to the similarity of ?K and K,a natural question would be whether the completeness of ?K can be shown as that of K;in more detail,in the construction of the canonical model,the canonical relation is defined aswRcviff ?-(w)?v,where?-(w)={φ∈L(?):?φ∈w}.The answer is negative.Consider the set
Note that Γ is consistent.10For this,it suffices to show that Γ is satisfiable.Construct a model M=〈W,R,V〉,which consists of two worlds s and t,sRt and tRs,and any propositional variable is true at both worlds.By induction on the structure of formulas,we can verify that M,s ?φ iff M,t ?φ for any φ ∈L(?).It then follows that M,s ??φ ?φ for all φ ∈L(?).Therefore,Γ is satisfiable.Then by Lindenbaum’s Lemma,there exists a maximal consistent setusuch that Γ ?u.Therefore,one may check that
Then according to the previous definition ofRcand the properties of maximal consistent sets,Rc(u)={u}.That is,uhas itself as its soleRc-successor.
Now thatucannot‘see’any of possible worlds other than itself,the semantics tell us thatu??⊥.However,as ⊥?u,we should have ?⊥?u.Therefore,the truth lemma fails.
In fact,not only those maximal consistent supersets of Γ above,but some maximal consistent supersets of{?φ→φ:φ∈L(?)}will lead to a failure of the truth lemma,and will require special attention(Def.6 below)for the sake of our completeness proof.For instance,consider a maximal consistent set that contains the following set of formulas Φ:
where Γi,Γjare pairwise different maximal consistent sets for everyi,j∈[1,n]such thati≠j.11We show such a maximal consistent set indeed exists via constructing a model.Consider a model which consists of n+1 worlds w1,w2,...,wn+1 such that w1 and w2 can ‘see’ each other,both of which can ‘see’ all other worlds, w1 and w2 agree on all propositional variables,the valuations on other worlds are not the same as w1 and w2,and also different with each other.One should easily verify that w1 and w2 agree on all L(?)-formulas.Let Γi={φ ∈L(?) : M,wi+1 ?φ} for each i ∈{1,...,n}and Γ=Γ1.We can then show that Γ and all Γi are maximally consistent,Γi ≠Γj for every i,j ∈{1,...,n}such that i ≠j,and Φ ?Γ.
All such maximal consistent sets have a common subset,that is,{?φ→φ:φ∈L(?)}.Chen ([6]) refers to such special sets as ‘problematic’ and collect them as T(L),in symbols,
Definition 6.[6,Def.2]Given any consistent normal extension L of ?K,define the canonical model ML=〈WL,RL,VL〉,where
·RL={((n1,w1),(n2,w2)) ∈WL×WL∣(n1,w1)=(n2,w2)or ?-(w1) ?w2}
·VL(p)={(n,w)∈WL∣p∈w}.
The reason for using copies in the case ofw∈T(L),is that,as explained before,aswmay have itself as its sole successor,copies can guaranteewto have a different successor.
Lemma 6.[6,Lem.3]LetLbe any consistent normal extension of?K.For all(n,w)∈WLand for all φ∈L(?),we have
Proof.By induction onφ∈L(?).The nontrivial case is ?φ.
Suppose that ?φ∈w,to show that ML,(n,w) ??φ.By supposition,φ∈?-(w).For all (m,v) ∈WLsuch that (n,w) ≠(m,v) and (n,w)RL(m,v),by definition ofRL,we have ?-(w) ?v,and thenφ∈v.By the induction hypothesis,ML,(m,v)?φ,for all such(m,v).Therefore,ML,(n,w)??φ.
Conversely,assume that ?φ?w.It is easy to show that ?-(w)∪{?φ}is consistent.Then by Lindenbaum’s Lemma,there existsu∈MCS(L)such that ?-(w)?uandφ?u.We distinguish two cases according to the value ofn:
·n=2.In this case,w?T(L).This means that for someχwe have ?χ∈wbutχ?w.As ?χ∈w,χ∈u,thusw≠u.Ifu∈T(L),we setm=0;otherwise,setm=2.Then (m,u) ∈WL.Becausew≠u,we have (n,w) ≠(m,u);since ?-(w) ?u,we infer that (n,w)RL(m,u).Fromφ?uand induction hypothesis,it follows that ML,(m,u)?φ.Therefore,ML,(n,w)??φ.
·n∈{0,1}.In this case,w∈T(L).Ifu∈T(L),we setm=1-n;otherwise,setm=2.Then(m,u)∈WL,andm≠n.Then we can also show that(n,w)≠(m,u),(n,w)RL(m,u)and ML,(m,u)?φ.Therefore,ML,(m,u)??φ.?
Theorem.[6,Thm.4]?Kis sound and strongly complete with respect to the classKof all frames,the classDof all serial frames,the classTof all reflexive frames.In symbols,for allX ∈{K,D,T},for allΓ ∪{φ}?L(?),we have
Proof.The soundness is straightforward.For completeness,note that M?Kis reflexive.Thus it suffices to show that every ?K-consistent set is satisfiable.
First,Lindenbaum’s Lemma tells us that every ?K-consistent set can be extended to a maximal ?K-consistent set,sayw.Ifw∈T(?K),then by Lemma 6,we have M?K,(0,w)?w;ifw∈,then by Lemma 6 again,we have M?K,(2,w)?w.This indicates thatwis satisfiable.Therefore every ?K-consistent set is satisfiable,as desired.?
- 邏輯學研究的其它文章
- On Types over p-adically Closed Fields
- The Interaction of Everyday Discourse and Professional Discourse—A Study of Generalized Argumentation in the Medicalization of Sleep*
- A Pragmatic Account for the Categorical Exchange between Content and Context*
- Sahlqvist Correspondence Theory for Modal Logic with Quantification over Relations*
- A Logic for Probabilities of Successive Events*

