Hybrid simulation of q=1 high-order harmonics driven by passing energetic particles in tokamak plasmas

Sheng LIU (劉勝) ,Zhenzhen REN (任珍珍) ,Weihua WANG (汪衛(wèi)華),* ,Wei SHEN(申偉) ,Jinhong YANG(楊錦宏) and Hongwei NING(寧洪偉)

1 Institutes of Physical Science and Information Technology,Anhui University,Hefei 230601,People’s Republic of China

2 School of Physics and Optoelectronic Engineering,Anhui University,Hefei 230601,People’s Republic of China

3 Institute of Plasma Physics,Chinese Academy of Sciences,Hefei 230031,People’s Republic of China

Abstract High-order harmonics q(ψs)=1 energetic particle modes(EPMs)have been observed in toroidal plasmas experiments with neutral beam injection.To investigate these phenomena,linear properties and nonlinear dynamics of these EPMs driven by passing energetic particles(EPs)are studied via the global hybrid kinetic-magnetohydrodynamic code M3D-K.Simulation results demonstrate that passing EPs’effects on high mode-number harmonics(q(ψs)=m/n=2/2,3/3,4/4) instability are more obvious than the q(ψs)=1/1 mode,especially when q-profile is sufficiently flat in the core region.Furthermore,the effects of the pitch angle Λ0 and beam ion pressure Phot/Ptotal on the features of high n components are also analyzed specifically.It is found that there exists only one resonant condition for these EPMs.In the nonlinear phase,these high mode-number harmonics can induce significant energetic ions redistribution and chirping up phenomena,which differs from the classical fishbone excited by passing EPs.These discoveries are conducive to better apprehend the underlying physical mechanisms of the highorder harmonics driven by passing EPs.

Keywords: high-order harmonics,passing energetic particles,wave-particle resonance,tokamak

1.Introduction

In magnetically-confined fusion devices,energetic particles(EPs) physics is a critical issue in achieving high confinement performance and steady-state operation.To increase the temperature of plasma,electron cyclotron resonance heating,ion cyclotron resonance heating and neutral beam injection(NBI) can be applied in tokamaks.In the process,a large number of EPs can be produced,which could interact with magnetohydrodynamics (MHD) activities or drive various instabilities including fishbone modes and Alfvén eigenmodes[1-6].Those instabilities can contribute to EPs loss/redistribution.In the Poloidal Divertor Experiment (PDX),fishbone instability excited by trapped particles was first observed under the perpendicular NBI[7].Subsequently,in the Princeton beta experiment (PBX) with tangential NBI,the fishbone-like internal kink modes excited by passing particles were also reported [8,9].Since then,in the last few decades,the experimental phenomenon of energetic ions acting on the q(ψs)=1/1 mode has been widely found in the tokamak experiments,for instance,Tokamak Fusion Test Reactor(TFTR) [10],Joint European Torus (JET) [11],HL-2A[12-14],and DIII-D [15].Furthermore,in comparison to q(ψs)=1/1 EPM,the instability of the high mode-number harmonics is also unstable which has been observed in MAST[16],EAST [17],ASDEX [18] and HT-7 [19] during NBI heating.Therefore,the study of high-order energetic particle modes (EPMs) excited by EPs in tokamaks is of great significance.

Theoretically,we can better apprehend the physical mechanisms of these MHD modes[20-24],including internal kinks,sawteeth,long livedmodes,and fishbones.In particular,the past related research reports have mainly focused on m=1,n=1 mode,which is resonantly excited by energetic ions generated from perpendicular or tangential NBI[25-29].When trapped particles excite the q(ψs)=1/1 mode,and the wave-particle resonance can be specifically expressed as ω=ωφ.When passing particles drive the q(ψs)=1/1 mode,and the wave-particle resonance can be specifically expressed as ω=ωφor ω=ωφ-ωθ[23,29-33],where ωφand ωθare the toroidal transit frequency and the poloidal transit frequency,respectively.m=n ＞1 EPMs are studied in recent years based on the experimental observations of these modes [34,35].Zhang et al numerically investigated q(ψs)=1/1,2/2 EPMs driven by trapped particles in tokamak[36].Up to now,the simulation results of the trapped particles affecting the high-order harmonics EPMs have been well reported[37].Nevertheless,it should be stressed that the impact of the passing EPs on the q(ψs)=1(n ≥1)harmonics were similarly observed in some experiments [38,39],and few simulation studies have been taken into account so far.The physical process of these n ＞1 EPMs can reduce the core plasma confinement,causing significant energetic-ion redistribution.To effectively achieve steady-state operation in tokamak plasmas,investigating the physical mechanism of high order harmonics driven by passing EPs is essential.

In this work,we concentrate our attention on the characteristics of the high-order harmonics EPMs,and numerically analyze the passing EPs impact on the mode excitation via M3D-K code [40].The rest of this work is organized as follows.In section 2,the simulation code and associated parameters are briefly introduced.In sections 3 and 4,the linear and nonlinear numerical results with passing EPs are presented,respectively.Ultimately,the summary and discussion are in section 5.

2.Numerical model and basic parameters

2.1.Physical analytical model

M3D-K is a global hybrid kinetic-magnetohydrodynamic(MHD) code,we mainly apply this code to numerically calculate the extended MHD equations and the drift-kinetic equations,respectively,which can better simulate the physical phenomenon of q(ψs)=1 EPMs in toroidal plasmas[25].The plasmas in this code are composed of the EPs and the background plasma.The EPs are demonstrated by driftkinetic equations,whose solution is δ? particle-in-cell method.The background plasma contains electrons and ions,which is considered as a solitary fluid in the MHD equations.The finite element method is used to calculate these equations.Up to now,M3D-K code was widely used to simulate MHD instabilities excited by EPs,such as fishbone mode,RSAE,EPM and TAE [41-47].

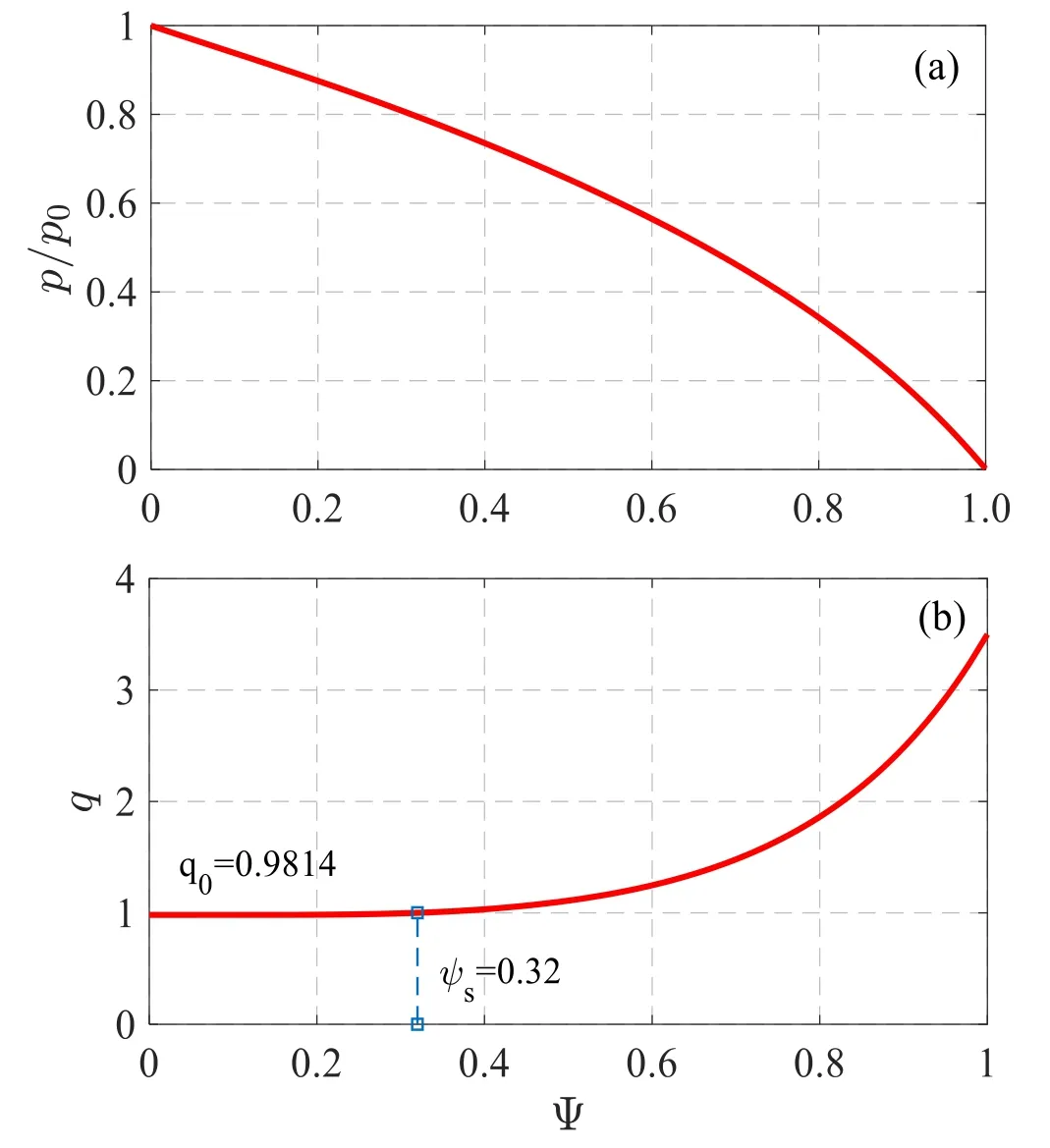
Figure1.(a) The pressure p equilibrium profiles and (b) q profile.

2.2.Equilibrium profiles and parameters setup

In this simulation,the main parameters are listed as follows based on HL-2A like conditions:circular cross-section,?-1=R0/a=3.6667,elongation κ=1,triangularity δ=0,B0=1.37 T,βhot/βtotal=0.5,the central total beta is fixed at βtotal=1.2%including the beta of both bulk plasma and EPs,E0=37.78 keV,where vA=B0/(μ0ρ0)1/2is Alfvén speed,τA=R0/vAis Alfvén time and ωA=vA/R0is Alfvén frequency.

Figure 1(a) shows the radial profile of total pressure,which is as follows:

where P0is pressure at the magnetic axis,the magnetic poloidal flux Ψ is a radial variable,the edge of the plasma Ψ=1,the center of the plasma Ψ=0.Correspondingly,for the q(Ψs)=1 EPMs,figure 1(b) is the spatial profiles of the safety factor with q0=0.9814.

The beam ion is a slowing down distribution in velocity space and Gaussian distribution in pitch angle space(Λ=μB0/E).The EPs distribution is as follows:

where ΔΨ=0.4,ΔΛ=0.3,Λ0=0.7,c is a normalization factor,H is the step function,vc=0.962vAis the critical velocity,which is as follows:

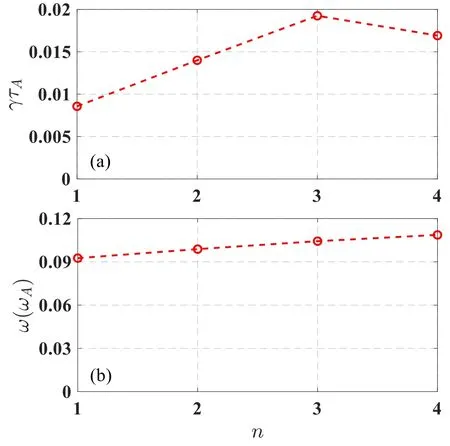
Figure2.(a)Growth rate from toroidal mode number n=1 to n=4 and (b) corresponding mode frequency.

3.Linear simulation results

3.1.Features of the high-order harmonics

In the linear simulation part of this work,Λ0=0.7 is chosen for analyzing the high-order harmonics,and the width of the pitch angle is set to be ΔΛ=0.3.Due to the impact of the pitch angle width,the distribution of pitch angle has a certain variation range,and the energy particles include passing particles and trapped particles in the beam ion distribution.In addition,according to wave-particle resonant interaction,we found that the high-order harmonics are driven by passing particles with Λ0=0.7,as shown in figure 4.These are the reasons why passing particles are analyzed with near perpendicular neutral beam injection in our work.

In the following the numerical results of the EPMs driven by passing EPs are presented.Initially,the numerical simulations without NBI are carried out,that is,MHD simulations are firstly performed,and these results show that MHD mode presents a steady state.Secondly,when NBI heating is included,according to the analysis of perturbed distribution δE,we find that the high order EPMs will become more unstable under the effects of passing EPs.As is shown in figure 2,passing EPs’effects on the q(ψs)=2/2,3/3,4/4 harmonics instability are more significant than those on the q(ψs)=1/1 mode,indicating that these high n component instabilities become more dominant.Furthermore,the mode frequency becomes higher when the toroidal mode number n increases.

It is shown in figure 3 that linear mode numbers of q(ψs)=1 EPMs are n=1,2,3,4,separately.U is the velocity stream function,which is associated with the plasma velocityν=R2??⊥U× ??+?χ+ν???,where the variables such as toroidal angle ? and compressible component χ are included.Due to the energetic ions’effect,the mode structures for these high order harmonics show slightly twisted feature,which is different from the typical internal kink mode.The mode structures are inside the q(ψs)=1 rational surfaces,which are denoted by the black circles.

Due to wave-particle resonant interaction,generally,the free energy of the radial variation of the EPs distribution excites the EPMs instability.For passing particles,the resonant condition expression is as follows [48]:

where p is an integer.Previous analyzes have initially focused on the q(ψs)=1/1 mode,satisfying the primary resonances with p=-1 for the EPMs branch of low-frequency or p=0 for the EPMs branch of high-frequency[31].In this work,we find that high frequency branch resonances can also be applied to high n harmonics.Figure 4 shows the perturbed fast ion energy δE in the phase space P?-E.The pitch angle parameter is fixed when we plot resonant conditions of different harmonics,where Λ is defined as Λ=μB0/E.When Λ is fixed,the resonance curves of the different harmonics are fitted and plotted in figure 4.To track the resonant locations,the significant changes of particle energy in the linear phase are investigated in figure 4,which shows the phase space locations of the particles with∣δE∣＞0.125Emax,whereδEis the particle energy change,Emaxis the maximum particle energy change.As a result,there are many particles with significant energy changes located along the resonant curves in figure 4.The magnetic moment values of these resonant particles vary in figure 4 with different energies.In addition,figure 4 shows that trapped particles are mainly centered in the regions of larger P?,while passing EPs are mainly centered in the regions of smaller P?.For the passing and trapped particles,we use the horizontal dashed lines as the dividing line of the different types of particles in figure 4.Significantly,the different harmonics with q(ψs)=1/1,2/2,3/3,4/4 modes have only one branch of resonance condition,with the resonance corresponding to p=0,-1,-2,-3 respectively.Furthermore,we observe that large δE for different harmonic modes are all located below the dashed line.Therefore,these simulations show that the resonance of waves and particles is caused by the passing EPs when Λ0=0.7.Because toroidal angular momentum can be expressed asP?=eψ+mDν‖RB?B,which is related to ψ.Compared to the q(ψs)=1/1 mode,n=2,3,4 components have a slightly smaller toroidal angular momentum P?,which indicates that locations of passing particle resonances are nearer to the core region of the tokamak plasmas.Generally,for energetic particle driven instabilities,the correlative growth rate expression isγ∝+[36],where P?is canonical toroidal angular momentum.This formula shows that the drive related to the special gradient of distribution is proportional to toroidal mode number n,which partially explains why n=2,3,4 components instabilities are more unstable compared to the n=1 component.Furthermore,it is shown in the following that the excitation of high order harmonics depends on the shape of q profile and various related parameters.

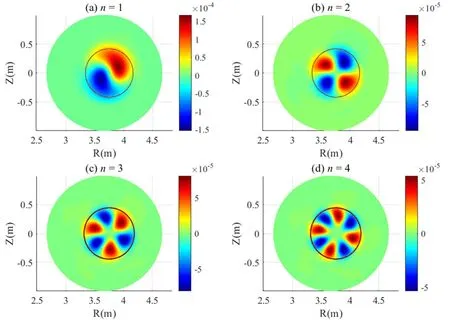
Figure3.The velocity stream function U.(a)The(1,1)harmonic,(b)the(2,2)harmonic,(c)the(3,3)harmonic and(d)the(4,4)harmonic.

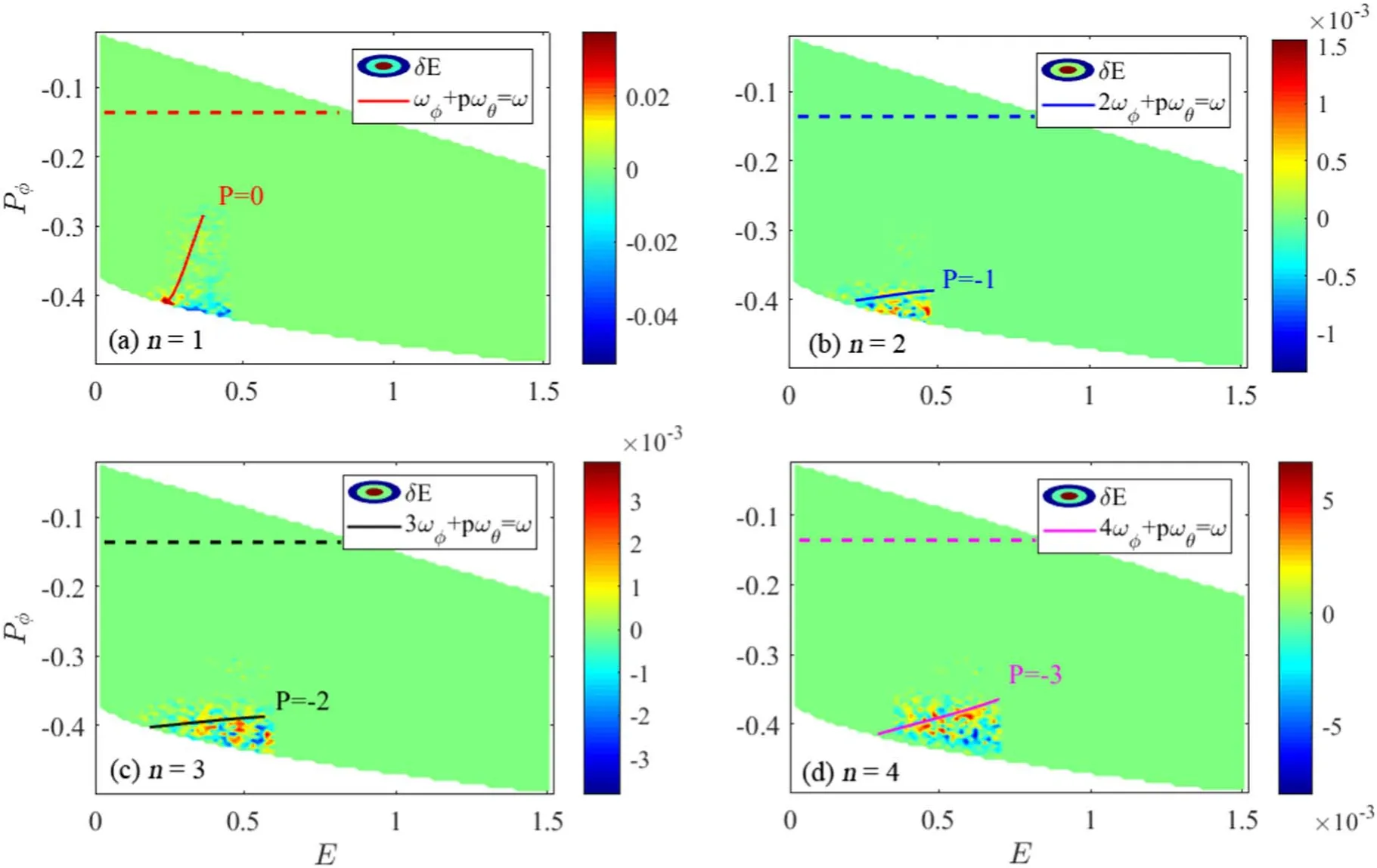
Figure4.The resonant conditions of different harmonics: including (a) the (1,1) harmonic,(b) the(2,2)harmonic,(c) the (3,3) harmonic and(d)the(4,4)harmonic.The horizontal dashed lines in figures 4(a)-(d)show the dividing line for the different types of particles.Above the dotted line is the trapped particles region,and below the line is the passing particles region.The color bar shows the amplitude of the energy change δE of energetic particles.

3.2.Effects of important parameters on high-order harmonics

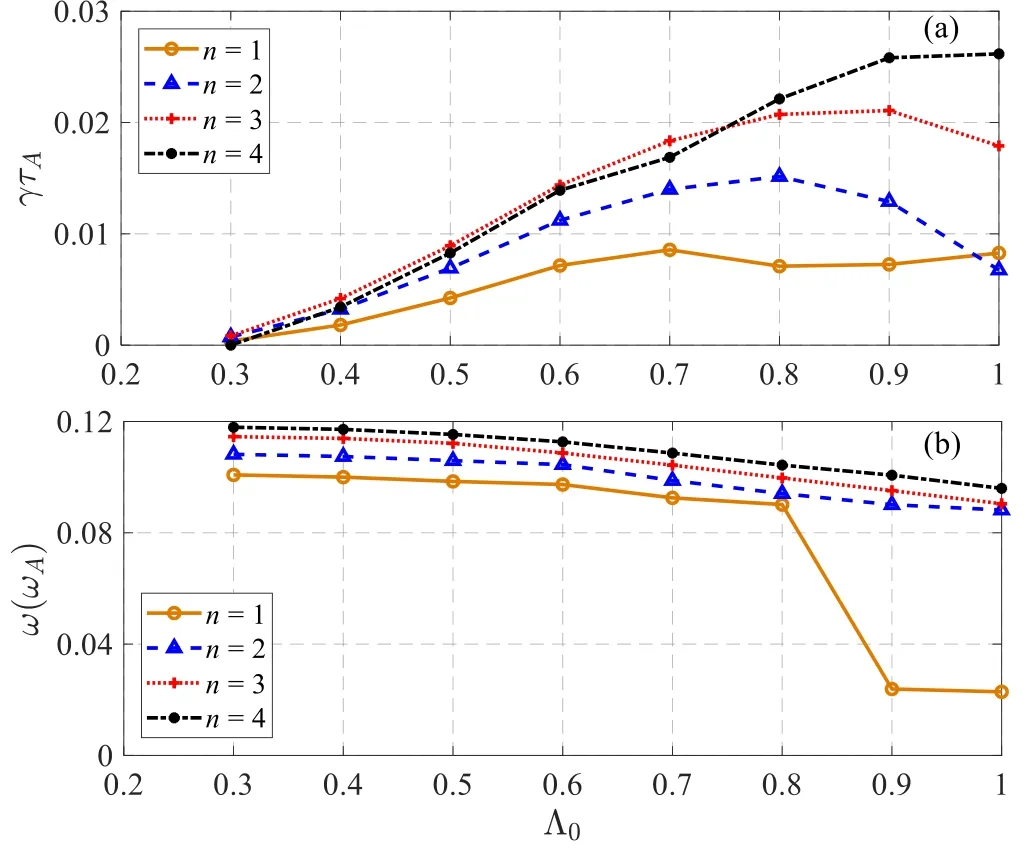
Figure5.(a) Growth rate of the q(ψs)=1 EPMs from pitch angles Λ0=0.3 to Λ0=1.0 and (b) corresponding mode frequency.

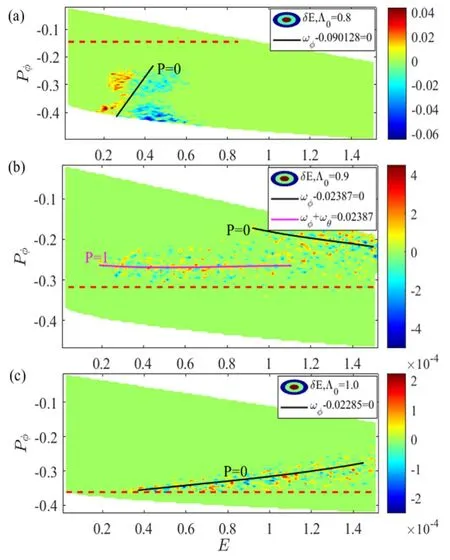
Figure6.Resonant condition: (a) Λ0=0.8,the mode frequency is 0.090128ωA,(b) Λ0=0.9,the mode frequency is 0.02387ωA and(c) Λ0=1.0,the mode frequency is 0.02285ωA for the q(ψs)=1/1 mode.

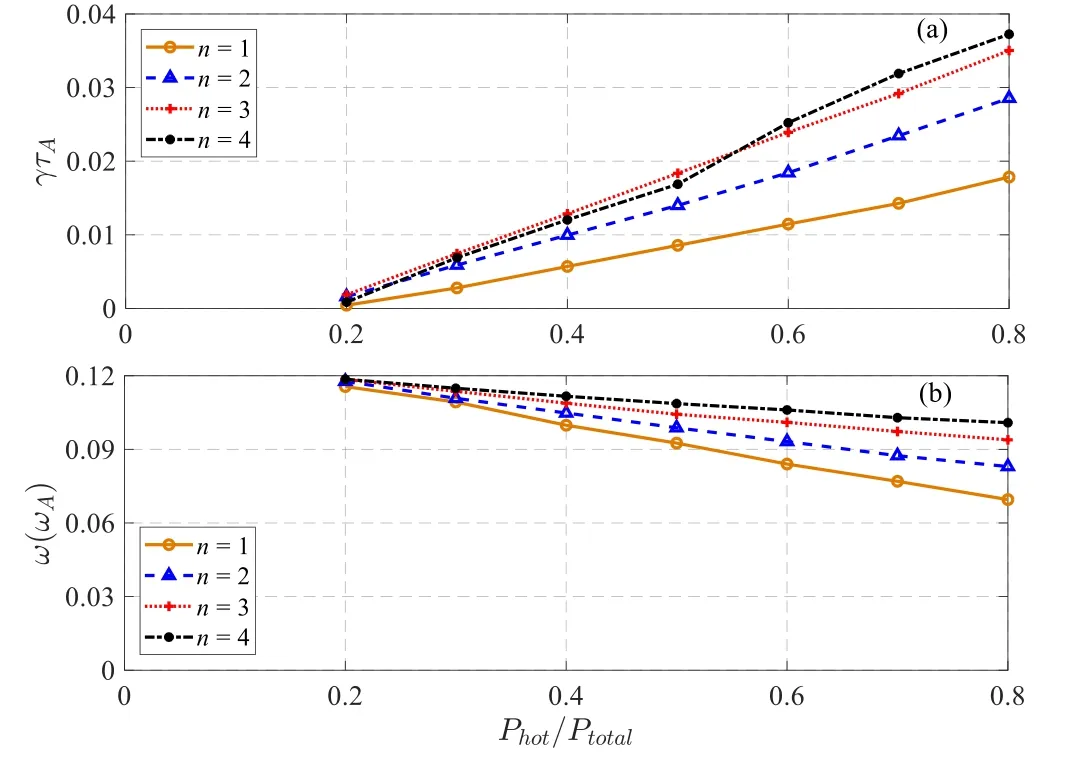
Figure7.(a) Growth rate of the q(ψs)=1 harmonics from the function of Phot/Ptotal=0.2 to 0.8 and (b) corresponding mode frequency.

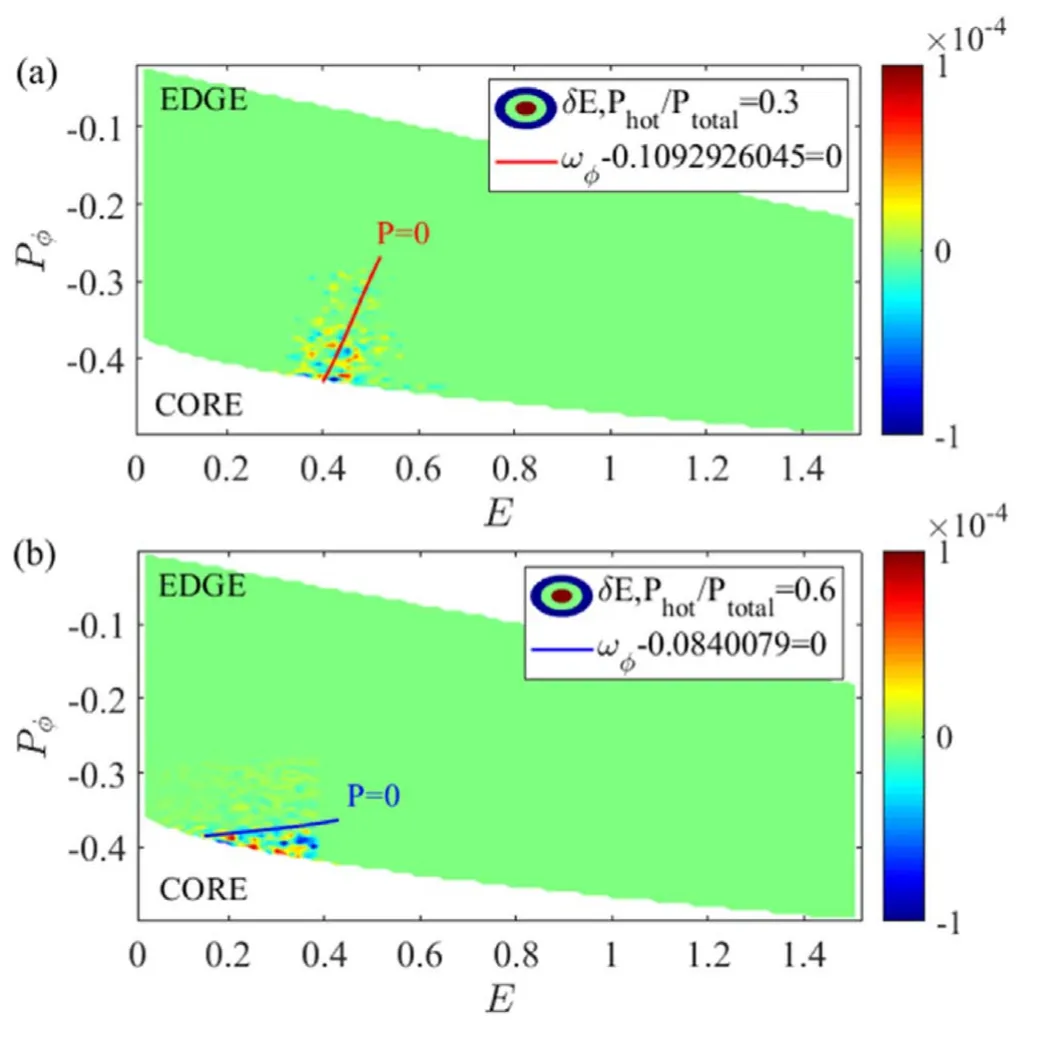
Figure8.Resonant condition: (a) Phot/Ptotal=0.3,the mode frequency of the n=1 mode is 0.1092926045ωA and (b) Phot/Ptotal=0.6,the mode frequency of the n=1 mode is 0.0840079ωA for Λ0=0.7.

To testify to the impact of the central pitch angle (Λ0),it is shown in figure 5 that the pitch angle varies from 0.3 to 1.0,which affects the mode frequency and instability of different harmonics.The q(ψs)=1(n ≥1)harmonics are stable in Λ0≤0.3.However,with Λ0increasing,the energy particles effect on the stability of these EPMs becomes more obvious.Furthermore,the linear frequency of these EPMs decreases as Λ0increases.The reason is that the transit frequency of passing EPs is determined by particle parallel velocity,associated with pitch angle Λ[49].According to the changes of the perturbed distribution δE,we mark the most prominent locations of the wave-particle resonance under different Λ0.For the n=1 component,Λ0=0.8,0.9,1.0 are chosen to analyze as the mode frequency changes significantly in this region.When Λ0=0.8,the modes are mainly excited by passing particles,while Λ0=0.9,1.0,the modes are mainly excited by trapped particles.The resonant results are shown in figures 6(a)-(c),when Λ0=0.8,the m=1,n=1 mode has only one resonant condition with p=0,and passing particles energy changes significantly below the red dashed line.However,when Λ0=0.9,the m=1,n=1 mode has two resonant conditions with p=0,1.When Λ0=1.0,the m=1,n=1 mode has also one branch resonant conditions with p=0.For both the EPMs with Λ0=0.9 and Λ0=1.0,particle energy changes are all located above the red dashed line,indicating that the impact of the trapped particles on the n=1 EPMs is dominant when Λ0≥0.9.

Figure9.(a)Spatial profiles of safety factor varying from q0=0.82 to q0=0.9814,(b)the corresponding linear growth rate for different toroidal mode numbers and (c) corresponding mode frequency.

As is illustrated in figure 7,with fixed total pressure,the effects of the EPs pressure fraction Phot/Ptotalon the excitation of the q(ψs)=1 (n ≥1) harmonics are examined,which become unstable when the EPs pressure over a certain threshold.As the beam ion pressure fraction Phot/Ptotalincreases,the growth rate of these EPMs gradually increases.However,the mode frequency of these EPMs decreases with the beam ion pressure increasing,which is mainly associated with the resonance locations.Taking q(ψs)=1/1 mode for instance,figures 8(a) and (b) respectively show the resonant conditions of different beam ion pressure fractions Phot/Ptotal,when Phot/Ptotalis smaller,the resonance locations of the passing particles are closer to the core.

In the previous study,it is found that the instability of the q(ψs)=1 modes is associated with δq=|q-1| [50].To testify the dependence of the q(ψs)=1(n ≥1)harmonics on the q-profile,we change q0from 0.82 to 0.9814 in figure 9(a).Figure 9(b)shows that the stability of these EPMs is sensitive to the safety factor and the flattened region of q-profile.For a smaller q0(q0=0.82),the n=1 component grows linearly at the rate of γτA≈0.005,but the high-order EPMs are stable.With q0gradually increasing and q-profile becoming more flattened,the instability of the high mode-number harmonics becomes very unstable,which is even more dominant when q0＞0.9.Furthermore,it is found that the mode frequency changes of the q(ψs)=2/2,3/3,4/4 components are different from the q(ψs)=1/1 mode in figure 9(c),whose mode frequencies with different q0are almost the same.

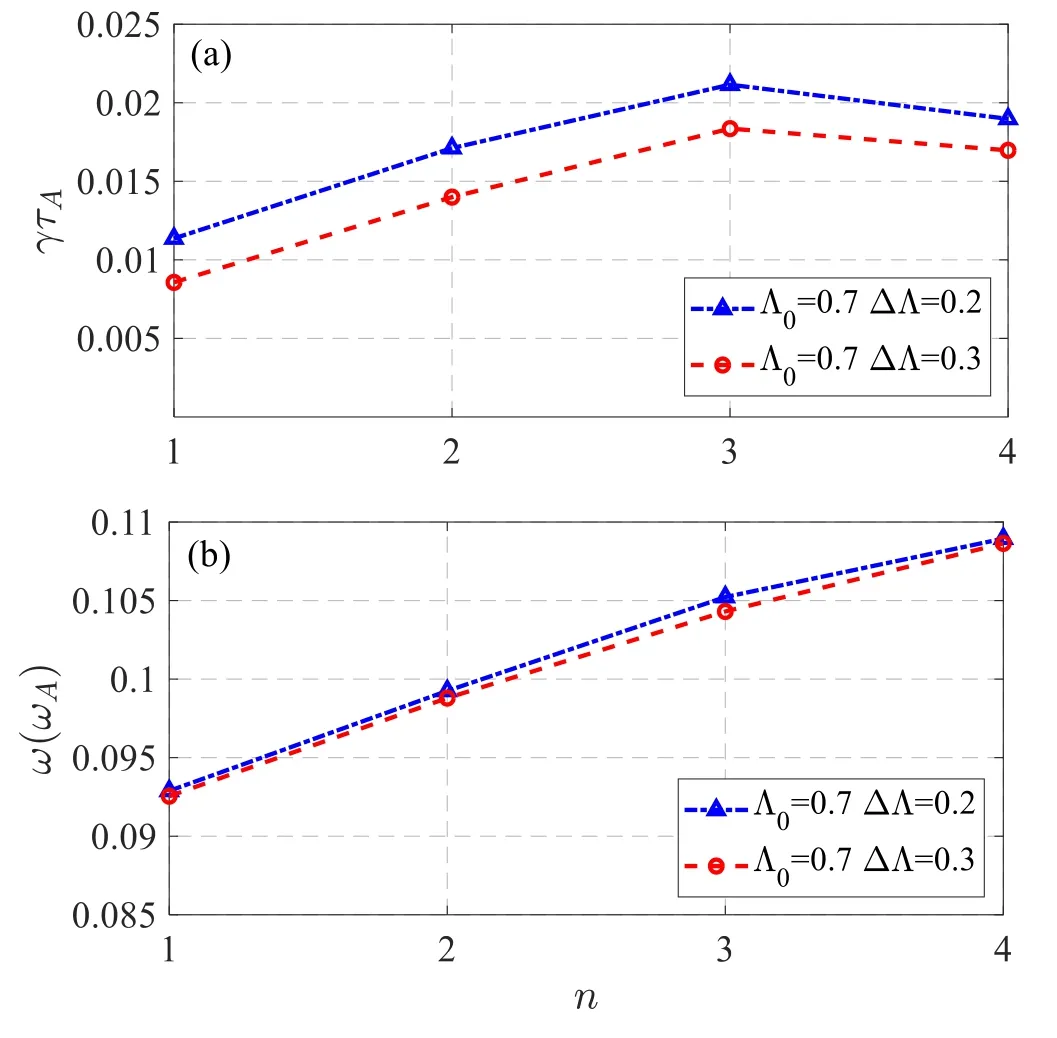
Figure10.(a)Growth rate of the q(ψs)=1 harmonics with different ΔΛ=0.2 and 0.3 and (b) corresponding mode frequency.

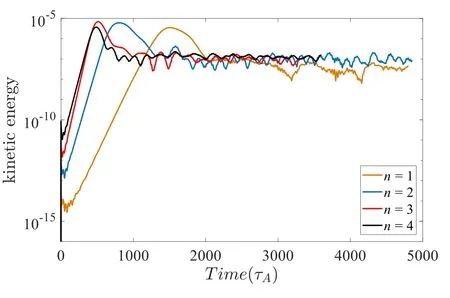
Figure11.Time evolution of the kinetic energy for different toroidal mode numbers.

In some experiments in HL-2A and EAST with flat q profile in the core region,the high order harmonics do not emerge.There are two possible explanations for this puzzle.Firstly,according to the theoretical work by Hastie and Hender [50],the stability criterion for higher m modes without energetic particle effects is given bywhereδq=∣q-1 ∣,r1is the radial location of q=1 surface.As a result,the stability of higher m modes depends on various parameters including the beta value,the location of q=1 surface,and the mode number.Secondly,in the following,we show that a few parameters related to EPs can also affect the linear growth rate of high order harmonics,including Λ,Phot/Ptotal,etc.As a result,although the condition of flat q profile is satisfied,the excitation of high order harmonics still depends on various related parameters,which explains why in some experiments the high order harmonics do not dominate with flat q profile.

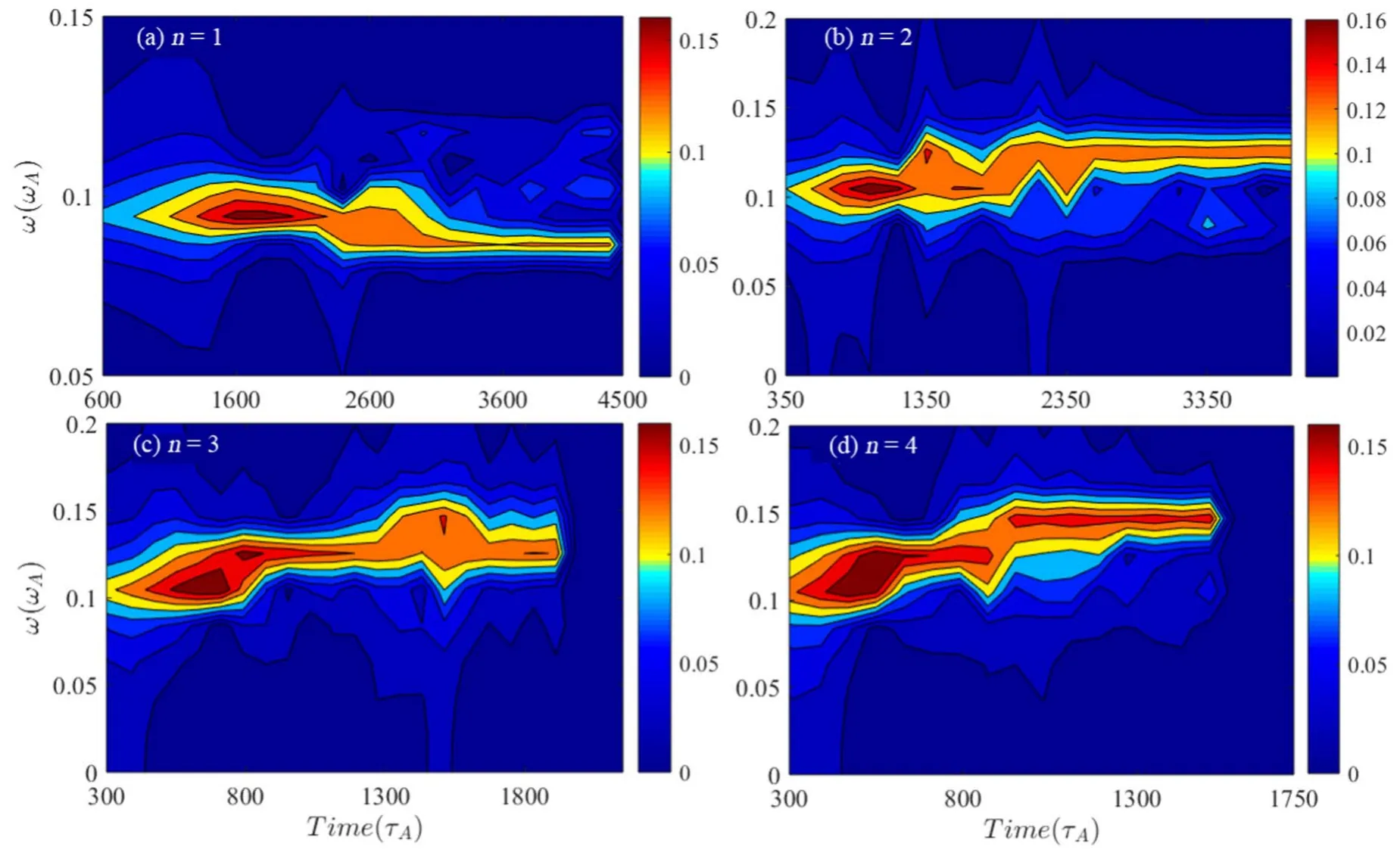
Figure12.Fourier spectrogram including (a) the (1,1) mode,(b) the (2,2) mode,(c) the (3,3) mode,(d) the (4,4) mode.

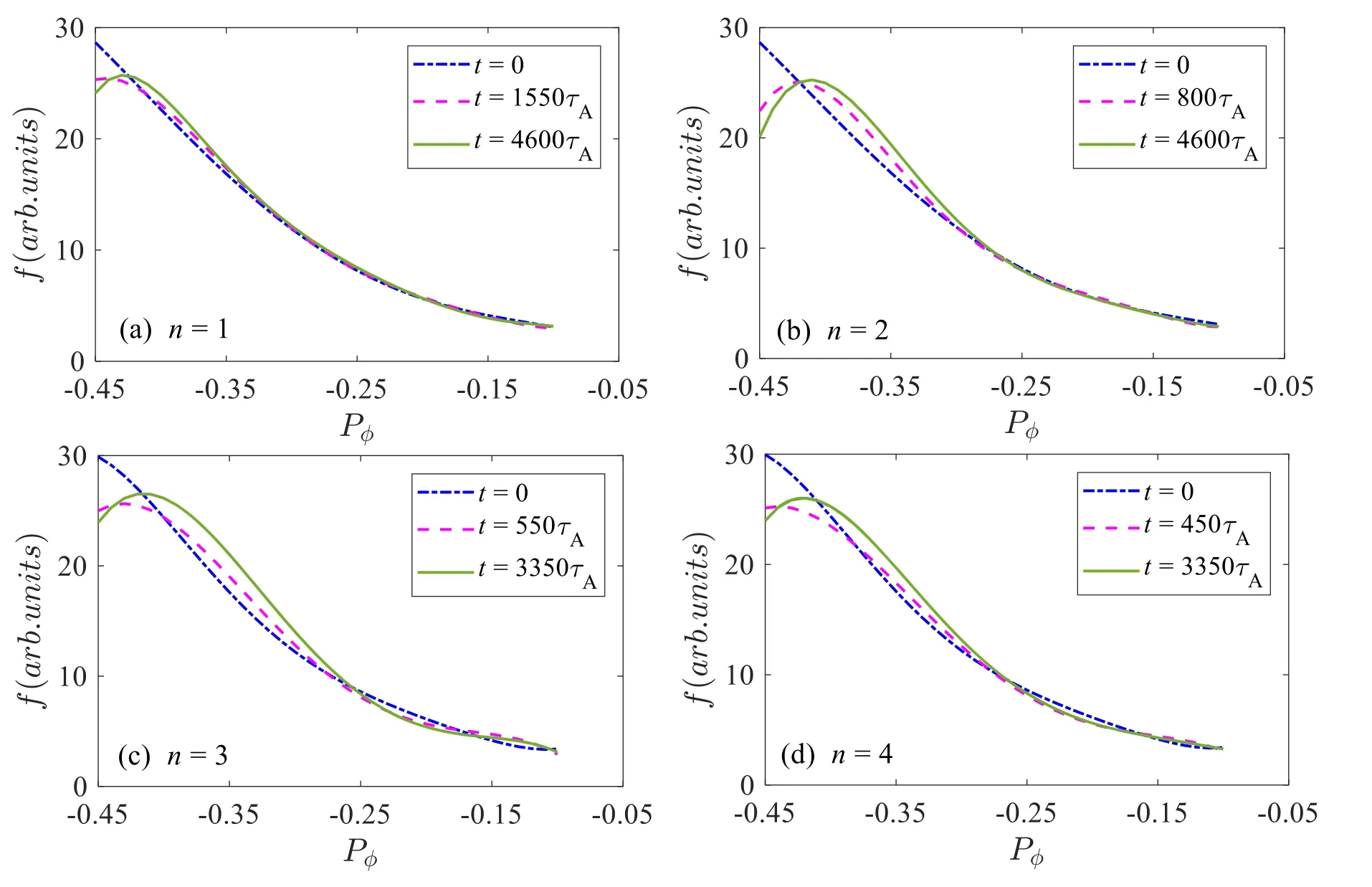
Figure13.Time evolution of 1D distribution function with (a) n=1,(b) n=2,(c) n=3,(d) n=4.

To better explore the impact of the pitch angle width on the high-order harmonics,Λ0=0.7 is chosen for analysis.The linear growth rates and mode frequencies are shown in figure 10,for two different ΔΛ: ΔΛ=0.2 (blue dashed line)and ΔΛ=0.3 (red dashed line),and the radial width is Δψ=0.4(ψmax-ψmin).The instability of different modes decreases with increasing the width of the pitch angle (ΔΛ),and the q(ψs)=1 high mode-number harmonics are still dominant compared to the n=1 component.However,the frequencies of different modes are nearly independent of ΔΛ.

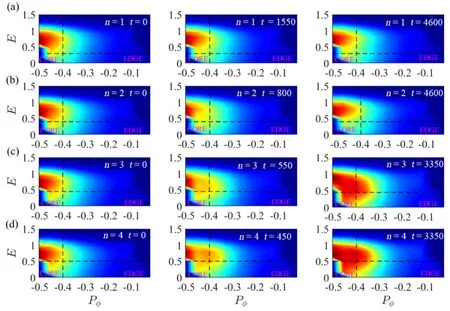
Figure14.Time evolution of 2D distribution function with (a) n=1,(b) n=2,(c) n=3,and (d) n=4.

4.Nonlinear simulation results

4.1.Saturation level analysis of different modes

In the nonlinear simulation part of this work,the kinetic energy evolution of different toroidal modes without MHD non-linearity is shown in figure 11.Here we choose Λ0=0.7,which is consistent with the linear simulations.Significantly,these high n components driven by passing EPs have larger saturation level in the nonlinear phase.Generally,the EPMs saturation is associated with the flattening of the particle distribution [25].In [37],it was proposed that the saturation levels of the q(ψs)=2/2,3/3,4/4 harmonics excited by trapped EPs are smaller than that of the q(ψs)=1/1 harmonic in the nonlinear phase.Nevertheless,the high mode-number harmonics driven by passing EPs are always dominant both in the linear and nonlinear saturation phases.These results are different from the previous work [37],in which the high mode-number harmonics driven by trapped EPs are just dominant in the linear phase.

4.2.Characteristics of the mode frequency

The phenomenon of frequency chirping in the nonlinear phase is caused by the wave-particle resonance.Figure 12 shows the frequency evolution of the high-order EPMs.For the q(ψs)=1/1 mode,the frequency shifts downward about δω/ω=13%.Nevertheless,the frequency of the high-order EPMs shifts upward.For the q(ψs)=2/2 mode,the frequency starts to stay around a constant value with no significant change,and then shifts upward about δω/ω=20% at around t ≈2500τA,and nearly no variation afterwards.Furthermore,the frequency evolution of the n=3 and n=4 parts is similar,where the chirping range is even larger,and shifts upward about δω/ω=41%at around t ≈1500τAand δω/ω=40%at around t ≈1200τArespectively.These physical phenomena of frequency chirping are due to the radial flattening of the EPs distribution,which may induce the resonance island shift in the phase space and cause the loss of energetic ions.

4.3.Evolution of energetic particles’distribution function

Due to the high-order harmonics instability,EPs generate redistribution in phase space.Figures 13(a)-(d) show the 1D distribution function ?(P?) of passing EPs.Firstly,in comparison with the nonlinear later phase,the redistribution levels are relatively small in the early initial saturation phase.Then,with the nonlinear time evolution of these EPMs,the redistribution of the beam ions expands outwards/inwards radially and has a large flattening region,located nearer the core region in the radial direction.Moreover,figures 13(b)-(d)show that the redistribution regions of the q(ψs)=2/2,3/3,4/4 harmonics are relatively larger than that of the q(ψs)=1/1 mode.There are two possible explanations for these results:(1)the ratios of the linear growth rate to the mode frequency are relative larger for the high n components.For instance,the n=1 component is γ/ω=0.093 while the n=3 component is γ/ω=0.175;(2)the saturation levels of the high mode-number harmonics are much higher,especially for the saturation peak of kinetic energy when n=3,which reaches the highest level.Consequently,the high mode-number harmonics can induce a more obvious redistribution of energetic ions.

Figures 14(a)-(d) show the 2D distribution function ?(P?) of passing EPs at E ≈0.3,0.4,0.46,0.5,which is marked by the horizontal black dashed.In addition,we plot the vertical black dashed at P?=0.4 in order to better observe redistribution.The movements of these particles in the phase space P?-E are determined by the formula[28].Here,the redistribution of EPs includes the first saturated phase and the later nonlinear phase.It is found that EPs have migrated from the core to the edge in the tokamak experiment.Especially with the nonlinear evolution of these EPMs,the levels of redistribution for the n=2,3,4 modes are further enhanced.Thus,the significant redistribution of energetic ions for the q(ψs)=1/1 mode is relatively smaller.As a result,energetic ions are transported in the phase space P?-E,indicating that the high-order EPMs can induce the redistribution of energy ions.

5.Summary and discussion

In summary,the linear and nonlinear evolutions of the q(ψs)=1 high mode-number harmonics driven by passing EPs have been systematically studied via the global kinetic-MHD code M3D-K.In the linear phase,the impacts of the important parameters are first analyzed in this work.With the central pitch angle or the energetic particle pressure increasing,the instability of these EPMs becomes stronger.Specifically,the transition of the wave-particle resonance condition from passing particles dominant to trapped particles dominant is observed when the central pitch angle exceeds a certain range.Furthermore,numerical results show that passing EPs’ effects on high mode-number harmonics instability are more significant than that on the q(ψs)=1/1 mode.The high-order EPMs driven by passing EPs satisfy different resonant conditions under different pitch angles.

Additionally,the nonlinear features of these EPMs have also been investigated.It is found that frequencies of the n ＞1 components chirp up,which is different from the classical fishbone.Ultimately,because high n components have a relatively larger saturated level,we find that strong redistribution of the passing EPs can be induced by the high-order harmonics.The instability phenomena of these EPMs driven by passing EPs can be commonly observed in HL-2A experiments.Therefore,the related discoveries in this work are conducive to guiding future tokamak experiments,especially in controlling the instability of high-order harmonics modes.

Acknowledgments

This work is supported by National Key R&D Program of China (Nos.2019YFE03050002,2018YFE0310400,and 2022YFE03040002),and National Natural Science Foundation of China (Nos.12005003 and 11975270),and Science Foundation of Institute of Plasma Physics,Chinese Academy of Sciences (No.DSJJ-2022-04).

ORCID iDs