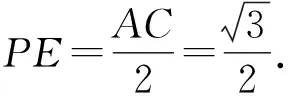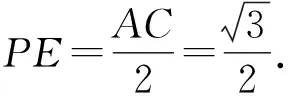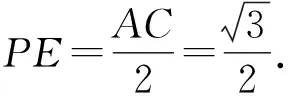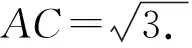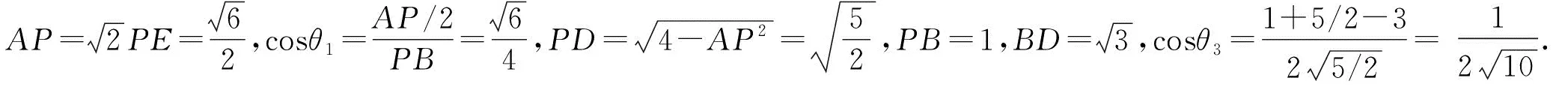對(duì)2022年一道立體幾何題多種解法的研究

劉大鵬

(遼寧省黑山縣第一高級(jí)中學(xué),遼寧 錦州 121400)

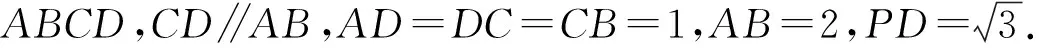
(1)求證:BD⊥PA;

(2)求PD與平面PAB所成角的正弦值.

1 解法展示

1.1 第(1)問解析

圖1 2022年全國(guó)甲卷18題

因?yàn)锳D2+BD2=AB2,所以BD⊥AD.

又因?yàn)镻D⊥面ABCD,BD?面ABCD,所以BD⊥PD,AD∩PD=D,所以BD⊥面PAD,PA?面PAD,所以BD⊥PA.

評(píng)注解法2用到了托勒密定理(圓的內(nèi)接凸四邊形兩組對(duì)邊乘積的和等于對(duì)角線的乘積),解法新穎,對(duì)拓寬學(xué)生的知識(shí)面及培養(yǎng)學(xué)生的發(fā)散思維能力都大有裨益.

1.2 第(2)問解析

在△DAE中,

DE2=1+x2-x,

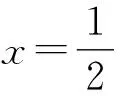
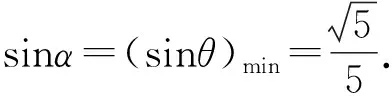
解法2 (定義法)如圖2,過點(diǎn)D作DF⊥AB于點(diǎn)F,連接PF,由PD⊥面ABCD,AB?面ABC,所以PD⊥AB.因?yàn)镻D∩DF=D,所以AB⊥面PDF.

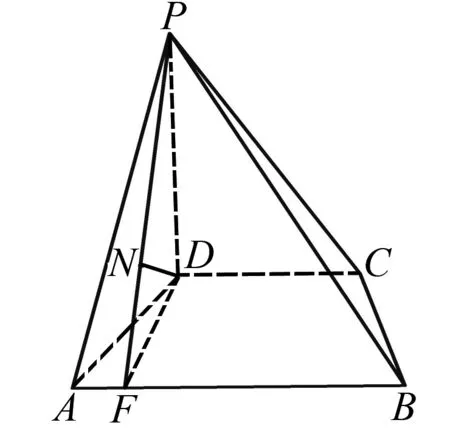
圖2 定義法圖

因?yàn)锳B?面PAB,所以面PDF⊥面PAB.

過點(diǎn)D作DN⊥PF于點(diǎn)N,則DN⊥面PAB.

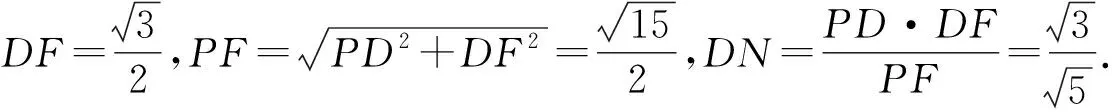
評(píng)注求點(diǎn)D到面PAB的距離,可以用等積法(即VP-ABD=VD-PAB),從而不必作輔助線.

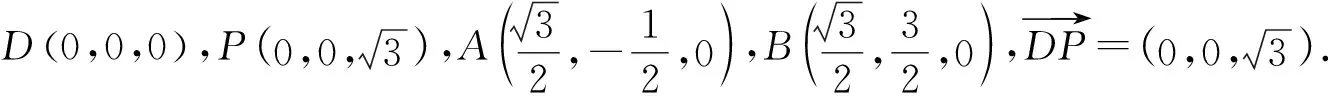
圖3 向量法圖

n=(2,0,1)是面PAB的一個(gè)法向量.

評(píng)注本解法用到了平面的點(diǎn)法式方程A(x-x0)+B(y-y0)+C(z-z0)=0,其中n=(A,B,C)是平面的一個(gè)法向量,P(x0,y0,z0)是平面上的一個(gè)定點(diǎn),用到了點(diǎn)M(x0,y0,z0)到面α:Ax+By+Cz+D=0的距離公式

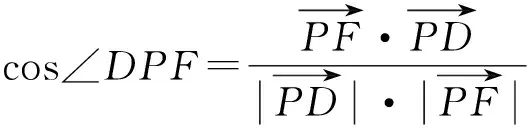
記直線PD與面PAB所成角為α,則

評(píng)注本解法建立了二元函數(shù)解析式,并用權(quán)方和不等式求出了函數(shù)最大值.

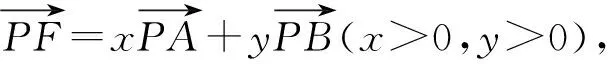
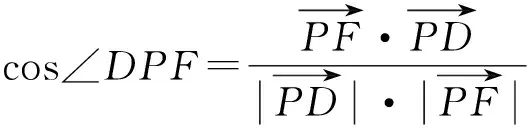
記直線PD與面PAB所成角為α,則

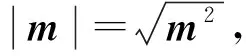
圖4 三面角圖

我們把它稱為三面角公式1.用它求二面角不需要作輔助線,非常方便,能提高解題速度.

解法7 由解法2知,PD和它在面PAB上的射影都與AB垂直,過點(diǎn)P作PE∥AB,則PD與面PAB所成的角等于二面角D-PE-A的值.

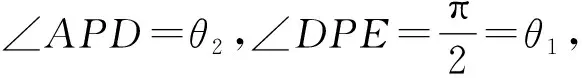
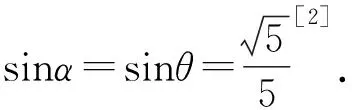
2 變式訓(xùn)練題及解法研究

變式在四棱錐P-ABCD中,底面ABCD是梯形,AD∥BC,AD=2BC,PA⊥PD,AB=PB=1,

(1)求證:PA⊥平面PCD;

(2)若BC=CD=1,當(dāng)四棱錐P-ABCD的體積最大時(shí),求直線PB與平面PAD所成角的正弦值.

本文只研究第(2)問的解法.

解法1 (利用最小角定理)由(1)得AP⊥PC.如圖5,取AC中點(diǎn)E,連接PE,四邊形ABCD是等腰梯形.

圖5 利用最小角定理解析

所以AC·BD=AC2=AB·CD+AD·BC=3.

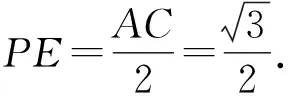
當(dāng)PE⊥面ABC時(shí),VP-ABCD有最大值,此時(shí)

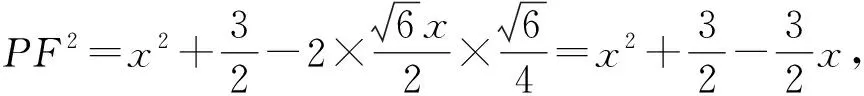
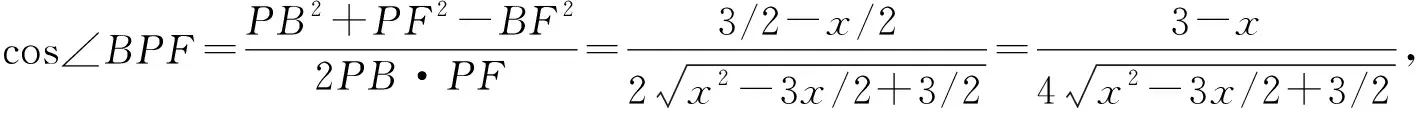
令t=3-x(1

記直線PB與面PAD所成角為α,則

α=(∠BPF)min,

解法2 (定義法)由(1)得AP⊥PC,取AC中點(diǎn)E,連接PE,四邊形ABCD是等腰梯形,

所以AC·BD=AC2=AB·CD+AD·BC=3.

當(dāng)PE⊥面ABC時(shí),VP-ABCD有最大值,此時(shí)

記B到面PAD的距離為h,由VP-ABD=VB-PAD,

所以AB·BD·PE=PA·PD·h.

記直線PB與面PAD所成角為α,則

解法3 (向量法)由(1)得AP⊥PC,取AC中點(diǎn)E,連接PE,四邊形ABCD是等腰梯形,

所以AC·BD=AC2=AB·CD+AD·BC=3.

圖6 向量法解析圖

解法4 (向量法)由(1)得AP⊥PC,取AC中點(diǎn)E,連接PE,四邊形ABCD是等腰梯形,

所以AC·BD=AC2=AB·CD+AD·BC=3.

記B到面PAD的距離為h,則

解法6 (向量法+最小角定理)由(1)得AP⊥PC,取AC中點(diǎn)E,連接PE,四邊形ABCD是等腰梯形,所以AC·BD=AC2=AB·CD+AD·BC=3.

當(dāng)PE⊥面ABC時(shí),VP-ABCD有最大值,