例析解析幾何中的垂直關(guān)系

安徽省碭山中學(xué) (235300) 蓋傳敏

垂直關(guān)系是解析幾何中的一種特殊位置關(guān)系,對于垂直關(guān)系我們往往需要進(jìn)行合理有效地轉(zhuǎn)化,然后進(jìn)行求解,下面結(jié)合實(shí)例談?wù)劥怪标P(guān)系轉(zhuǎn)化的若干途徑.

1 斜率與垂直關(guān)系的轉(zhuǎn)化

例1 若直線l1:x-2y+5=0與直線l2:2x+my-6=0互相垂直,則實(shí)數(shù)m=________.

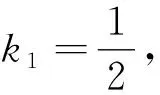
評注：在運(yùn)用斜率判定兩直線垂直時(shí),首先要對直線斜率的存在性進(jìn)行討論,若兩直線的斜率存在且不為0,可將兩直線垂直可轉(zhuǎn)化為兩直線的斜率乘積等于-1進(jìn)行求解.

2 向量與垂直關(guān)系的轉(zhuǎn)化

例2 已知點(diǎn)M(-1,1)和拋物線C:y2=4x,過C的焦點(diǎn)且斜率為k的直線與C交于A,B兩點(diǎn).若∠AMB=90°,則k=________.

評注：將直線之間的垂直關(guān)系轉(zhuǎn)化為向量之間的垂直關(guān)系,再轉(zhuǎn)化為向量的數(shù)量積為0進(jìn)行求解.

3 勾股定理與垂直關(guān)系的轉(zhuǎn)化

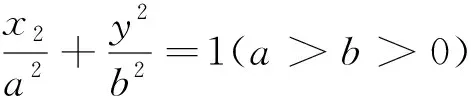
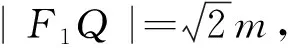
評注：通過垂直關(guān)系構(gòu)造適當(dāng)?shù)闹苯侨切?再利用勾股定理找出邊角之間的關(guān)系進(jìn)行求解.

4 圓與垂直關(guān)系的轉(zhuǎn)化

評注：由平面幾何知識可知圓中的直徑所對的圓周角是90°,因此通過垂直關(guān)系可構(gòu)造適當(dāng)?shù)膱A,然后利用圓的性質(zhì)進(jìn)行求解.

5 隱性的垂直關(guān)系

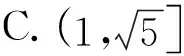
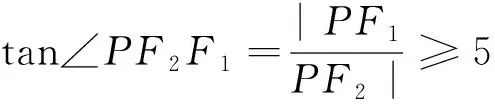
評注：如果題設(shè)條件沒有直接給出垂直關(guān)系,這時(shí)需要借助幾何圖形性質(zhì)挖掘垂直關(guān)系,然后進(jìn)行合理轉(zhuǎn)化再進(jìn)行求解.