Constructing the three-qudit unextendible product bases with strong nonlocality

Bichen Che(車碧琛) Zhao Dou(竇釗) Xiubo Chen(陳秀波)

Yu Yang(楊榆)2 , Jian Li(李劍)2, and Yixian Yang(楊義先)1

1Information Security Center,State Key Laboratory of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China

2Information Security Center,Beijing University of Posts and Telecommunications,Beijing 100876,China

Keywords: strong nonlocality,unextendible product bases,tri-tile structure,construction method

1. Introduction

With its potential applications, quantum information has brought new changes to the information industry.[1–4]Entanglement between quantum states is a kind of quantum resource, which can be used to achieve tasks that cannot be accomplished by classical resources,[5–8]such as quantum teleportation,[9,10]quantum algorithm,[11–13]and quantum dense coding.[14]For a long time,it has been believed that the nonlocality is closely related to properties of entangled states.However,in 1999,Bennettet al.[15]proposed a set of orthogonal product states with nonlocality,which aroused a wide discussion on the relationship between entanglement and nonlocality.

Unextendible product bases(UPBs)are a class of incomplete orthogonal product states, whose complementary space does not contain product states.[16–18]They cannot be distinguished perfectly by local operations and classical communication (LOCC). Researchers[19–21]have shown that it can be used in the production of bound entangled (BE) states and some special bipartite entangled states that remain positive under partial transpose (PPT). Nevertheless, most of the current efforts are devoted to the construction of 2-qubit UPBs,[22–24]while a little progress has been made on multiqudit UPBs.[25,26]Chenet al.[22]investigated the minimum size of UPBs with local dimension of 2,and analyzed the proposed sets using orthogonal graphs.Bejet al.[23]proposed that a set of reducible unextendible product states(UPSs)with high dimension can be obtained by adding several orthogonal product states on the bases of a set of UPSs with low dimension in a bipartite system. Recently, a method to construct UPBs of different sizes inCm ?Cnwas put forward by Shiet al.,[24]which usesU-tile structure. Shiet al.[25]also constructed the strongly nonlocal UPB in a tripartite system, which containsd3-4d+4 states whendis odd, and containsd3-4d+8 states whendis even. Multi-qudit UPBs are not only valuable in quantum circuit construction or cryptography experiments,but also often used to construct tight Bell inequalities without quantum violations.[27]Therefore, a general construction method for multi-qudit UPBs, especially for the system with any dimension,is needed,which is the first motivation of this paper.

As one of the research hotspots in quantum information theory, the quantum state discrimination problem is the basis of other quantum problems.[28–30]The distinguishable quantum states can be applied to some quantum information processing tasks, such as distributed quantum computing,while the indistinguishable quantum states are very common in design of quantum cryptography protocols. Bennettet al.[31]proposed the theorem that any set of orthogonal product states in 2?Nare distinguishable by LOCC.Zhanget al.[32]gave a general method to construct indistinguishable multipartite orthogonal product states inCd1?Cd2?···?Cdn（Cd1,2,···,n ≥3,n ≥4）. In addition to the above work,Halderet al.[33]recently found that in some nonlocal tripartite systems, when two parties measure together, there is a possibility that the shared state can be distinguished. Hence, the concept of strong nonlocality has been proposed and widely discussed. Based on Halder’s work, Zhanget al.[34]constructed two sets of quantum states with strong nonlocality,C3?C3?C3andC3?C3?C3?C3. Shiet al.[35]provided the process of constructing a set consisting of entangled states in theCd ?Cd ?Cdsystem based on Rubik’s cube. However,there is no relevant research on the construction of multi-qudit UPBs with strong nonlocality,which is the second motivation of this study.

Graph theory is an effective representation to help intuitively analyze the abstract structure of state sets.[36,37]It is also widely used in the construction of quantum state sets,[38–40]especially UPBs.[31,41–43]Johnstonet al.[37]analyzed the structure of UPBs in（C2）?pand proposed the minimum size of this quantum system by using the orthogonal graph. Bennettet al.[31]first proposed a tripartite UPB and provided two classical construction methods based on the graphs, namely, pyramid structure and tile structure. Hence,our third motivation is to use graph theory to analyze and display the internal structure and relations of the strongly nonlocal states.

Therefore,based on the above three motivations,the main focus in this paper is to construct a general set of 3-qudit UPBs with strong nonlocality. First, based on the shift UPBs, a UPB set inC3?C3?C3is obtained. By observing the orthogonal graph of each qutrit and the corresponding 3×3×3 Rubik’s cube, the structure of the states set and the relationship between qudits are analyzed in Figs.3 and 4. Then,following this construction method, we give a general 3-qudit UPB with strong nonlocality of size(d-1)3+2d+5 for theCd ?Cd ?Cdsystem. The general expression of the states set is provided in detail. Second, after reviewing the connection between UPBs and tile structure, we extend the tile structure from 2-qubit to 3-qudit systems and propose the tritile structure in definition 5. Moreover, by applying proposition 1, we generalize the construction ofC4×C4×C5and show a general approach to construct a strongly nonlocal UPB setCd1?Cd2?Cd3based on a UPB set with low dimension,C(d1-1)?C(d2-1)?C(d3-1). Our research provides a general form of UPBs with strong nonlocality, which can be further applied in many quantum protocols to fundamentally ensure its security.

The rest of this paper is organized as follows. In Section 2, we briefly introduce the notations and several preliminaries of UPBs. Sections 3 and 4 consist of the main contributions of the present work. Based on graph theory, the general construction method of 3-qudit UPBs with the same dimensions and different dimensions are proposed. Finally,we summarize the results and discuss some open problems in

Section 5.

2. Notations and preliminaries

In this section, we briefly introduce the preliminary knowledge and some notations. A multi-qudit pure state|v〉∈Cd1?···?Cdpis considered to be separable if and only if it can be written in the form

UPBs are nonlocal and cannot be perfectly distinguished by LOCC. However, when discussing the nonlocality of a multi-qudit system, it is found that there is a certain probability that states can be distinguished when several qudits are joined. Based on this phenomenon, the definition of strong nonlocality is given.

Definition 2: Locally irreducibility[40]A set of orthogonal product states on?=?ni=1?i,n ≥2,dim?i ≥2 is locally irreducible if it is impossible to eliminate one or more states from the set by orthogonality-preserving local measurements.

Definition 3: I-irreducible system In a multiparty systemCd1?Cd2?···?Cdn(d1,2, ..., n ≥3, n ≥4), if a set of orthogonal product states is arbitrarily divided intoiparts and the entire system is still locally irreducible in every newiparts, then the system can be called beingi-irreducible,i=2,3, ..., n-1.

Definition 4: Strongly nonlocal system InCd1?Cd2?···?Cdn(d1,2, ..., n ≥3, n ≥4), if a set of orthogonal product states is (n-1)-irreducible, (n-2)-irreducible,..., and 2-irreducible simultaneously, we can say that this system is strongly nonlocal.

For the measurement of nonlocal state sets, multiple rounds of measurement are required for multiple participants.Therefore, the nontrivial orthogonality-preserving measurement shall be required to obtain useful information without affecting the characteristics of the state set, which is defined in Definition 4.

Definition 5: Nontrivial orthogonality-preserving measurement[45]If a set of mutually orthogonal quantum states remain mutually orthogonal after measurement, the measurement used to distinguish the quantum states is defined as orthonormal preserving measurement(OPM).Furthermore,such a measurement is called being nontrivial if all the measurement matrices constituting the OPM are not proportional to the identity operator,otherwise,it is trivial.

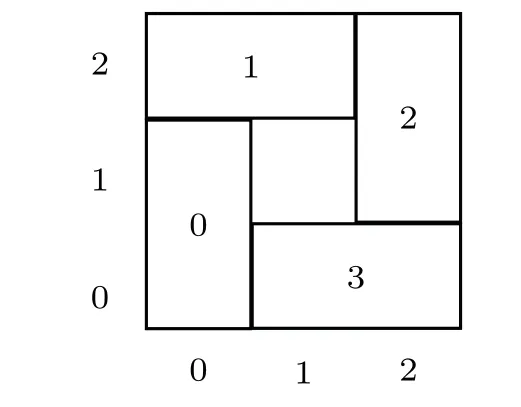
Fig.1. Tile structure.

Example 1: The setΨrepresents UPBs in theC3?C3system denoting the tile structure.

From Fig.1,we obtain a set of complete orthogonal product bases as Eq.(1),which are denoted asΦ:

These UPBs can be simply generalized to a UPB set over any number of parties,each with a one-qubit Hilbert space(see Ref. [19]). In this paper, the construction of 3-qudit UPBs is also based on the structure of the shift UPBs.

3. Tripartite system with same dimensions

In Ref.[31], it is proved that members of a UPB are not perfectly distinguishable by LOCC, that is, UPBs is always nonlocal. Then, we set out to investigate what kind of structure of multi-qudit UPBs is strongly nonlocal.

In Ref.[43], it was shown that starting from a two-qubit unextendible entangled basis,it is possible to construct a threequtrit unextendible entangled basis. Therefore, in this section, we give a construction method of the strongly nonlocal UPBs inC3?C3?C3based on shift UPBs in Lemma 1.Similarly, we propose the set of UPBs inC4?C4?C4in Lemma 2.Furthermore,we generalize these two constructions toCd ?Cd ?Cdfor anyd ≥3 in Theorem 1.

3.1. Construct a UPB in C3 ?C3 ?C3 system based on shift UPB

Shift UPBs is the most classical 3-qubit UPBs available.When its structure is represented by Rubik’s cube, it can be found that any subset of three vectors on either side spans the three-dimensional space of that party,[31]preventing any new vector from being orthogonal to all the existing ones. Following this idea,aC3?C3?C3state set is obtained as

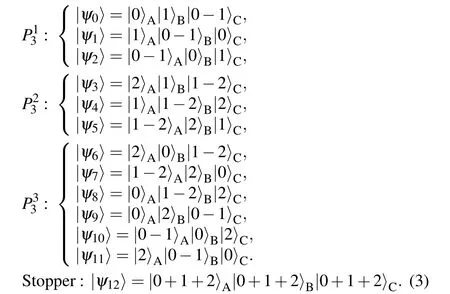
Fig.2. Rubik’s cube corresponding to C3 ?C3 ?C3.

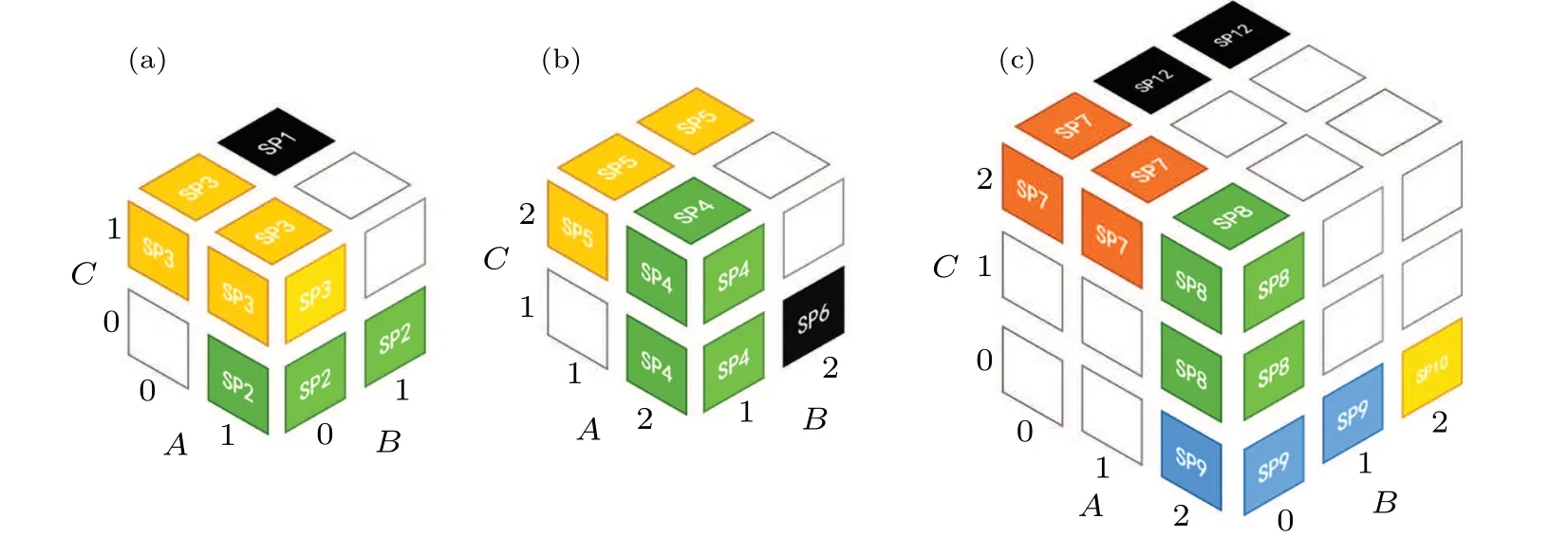
Fig.3 Composition of UPBs in C3 ?C3 ?C3.

By observing Rubik’s cube,some of the cuboids need to be merged to ensure the principle(see definition 1 in Ref.[42])that the combination of any two cuboids cannot become a new cuboid. The new merged states corresponding to the cuboids are shown in Eq.(4). In this set,we find that any two of these vectors are not in a two-dimensional plane.

Therefore,only the properties of one qutrit need to be discussed, and then the properties of three qutrit can be inferred from equivalence. From the composition of the basis, it is obvious that these states have a cyclic property as the cyclic property of the trace. That is to say,the state set has the same properties in the different divisions ofA|B|C,B|C|AandC|A|B.

Lemma 1 InC3?C3?C3,the 3-qutrit UPBs of size 19 given by Eq.(4)is strongly nonlocal.

Proof The proof can be summarized into two steps. The first step is to prove that this 3-qutrit system is nonlocal. This step can be omitted in the UPB set since UPBs are incomplete and nonlocal.

The second step is to prove that the whole system is still nonlocal with any partitioning method for three qutrits.

Physically, this method of division means that the subsystemsB(Bob) andC(Charlie) are treated together as a 9-dimensional subsystemBCon which joint measurements are now allowed. On account of the original UPB set is nonlocal,so the system will be still nonlocal when Charlie goes first.Then,we only need to discuss the situation where theBCsystem goes first. In order to make the proof process clearer,we first rewrite the original state, let|00〉 →|0〉,|01〉 →|1〉, ...,|22〉→|8〉. After rewriting the state in Eq. (4), we can get the following states:

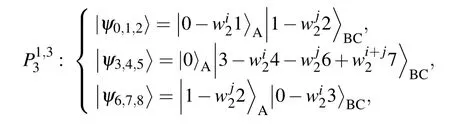
The 18 states inA|BCbipartition correspond to 6 blocks of the 3×9 grid in Fig.5. It can be seen that this whole graph is centrosymmetric.

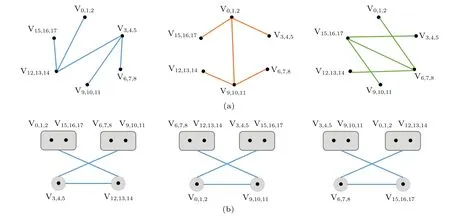
Fig.4. Orthogonal graph of three qutrits.

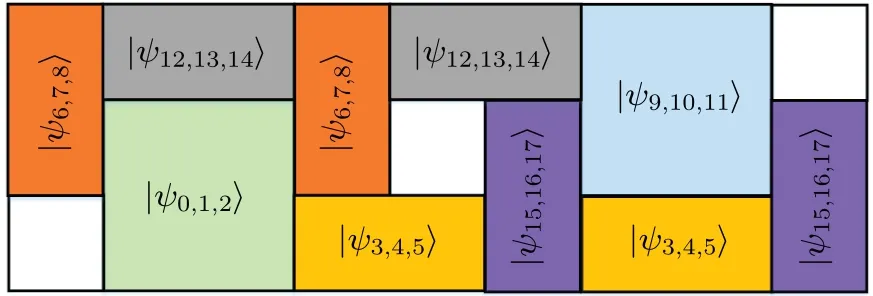
Fig.5. The corresponding 3×9 grid of Eq.(5).

Therefore,the original matrix can be reduced to

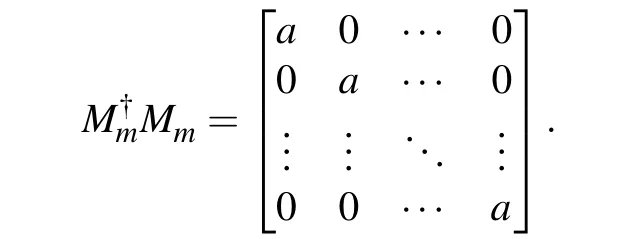
Table 1 shows the detailed derivation process.

Obviously,BC’s measurement matrix is proportional to the identity matrix,so it means that theBCsystem starts with a trivial measurement, and cannot get any information about shared state distinction from the measurement result. As for the other two division methods,B|CAandC|AB, the proof method is similar to this. In summary,the three qutrits divided into any two parts can keep the strong nonlocality of UPBs.

3.2. Construct a UPB in C4 ?C4 ?C4 system based on a UPB in C3 ?C3 ?C3 system

Based on the construction method of state set in Eq.(4),we extend UPBs to the case of dimension equal to 4. Compared with Rubik’s cube of 3×3×3, the cube of 4×4×4 has three new planes,{(0,...,3)A,(0, ...,3)B,3C},{(0,...,3)A,3B,(0,...,2)C},{3A,(0,...,2)B,(0,...,2)C}.According to tile structure,we obtain Fig.6.

Table 1. POVM elements.

Fig.7. Composition of UPBs in C4 ?C4 ?C4.

By matching Rubik’s cube with the states set, we get Eq.(6). Compared withC3?C3?C3,there is one more part,

3.3. Construct a UPB in Cd ?Cd ?Cd system based on a UPB in Cd-1 ?Cd-1 ?Cd-1 system

After analyzing the structure of UPBs proposed in Lemma 1 and Lemma 2, we give a UPB inCd ?Cd ?Cdof size(d-1)3+2d+5 based on the set inCd-1?Cd-1?Cd-1,and then obtain Proposition 1.

The general 3-qudit UPB set is always built on the basis of lower dimensional state set, like an onion. First, the three planes,{(0, ..., d-1)A, (0, ..., d-1)B,(d-1)C},{(0, ..., d-1)A,(d-1)B,(0, ..., d-2)C},{(d-1)A,(0, ..., d-2)B,(0, ..., d-2)C}are divided into different nonlocal cuboids. Then, the remaining part is a tripartite system with dimensiond-1. Again, we divide the three planes,{(0, ..., d-2)A, (0, ..., d-2)B,(d-2)C},{(0, ..., d-2)A, (d-2)B, (0, ..., d-3)C},{(d-2)A,(0, ..., d-3)B, (0, ...,d-3)C}in the same way. Continually, until a 3-qubit UPB withd= 2 is left, it will be divided according to the shift UPBs.

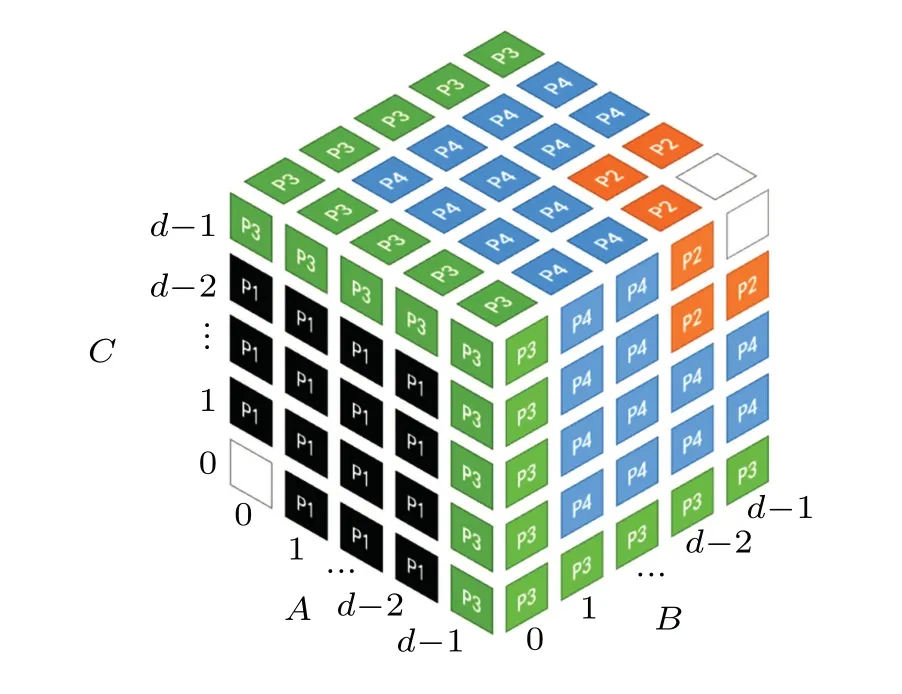
Fig.8. Composition of UPBs in Cd ?Cd ?Cd.

Proposition 1: InCd ?Cd ?Cd, the UPBs of size(d-1)3+2d+5 given by Eq.(7)is strongly nonlocal.

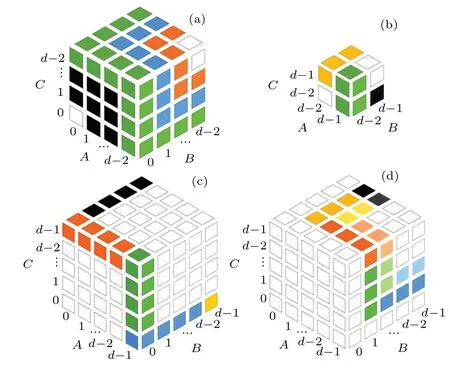
Fig.9. Composition of UPBs in Cd ?Cd ?Cd.

In addition,there are also some product states in the process of construction that are not orthogonal to the stopper state|S〉but orthogonal to all states inΨ?{|S〉}.We call these states missing states. It is valuable in the discussion of BE states.Any state in the complementary subspace?⊥ψis a linear combination of the missing states.

4. Tripartite system with different dimensions

In the above section, UPBs with the same dimensions of three parties are discussed. In this section, we continue to discuss another scenario which is more general in tripartite systems and propose a set of strongly nonlocal UPBs inCd1?Cd2?Cd3.

4.1. Construct a UPB in C3 ?C3 ?C4 system with strong nonlocality

The tile structure is a classical approach in the general construction of 2-qubit UPBs, which was first proposed by Bennet in 1999. Later,many researchers studied the tile structure and some related structures are proposed,such as the Gen tile structure. In tile structures, any two sub-rectangles (i.e.tiles)cannot be combined to form a new rectangle by a simple translation. Following this method, we consider whether tile structures can be extended to the 3-qudit.

The tripartite state setCd1?Cd2?Cd3can always be uniquely mapped to a Rubik’s cube whose section is one of the three planes,Cd1?Cd2,Cd2?Cd3andCd1?Cd3. Therefore,we extend the classical tile structure to three parties,which is defined in the following.

Definition 5: Tri-tile structure If two sub-cuboids(i.e.,tiles)cannot be combined to form a new cuboid(i.e.,tiles)by a simple translation,then the structure of the state set is defined as the tri-tile structure.

Moreover,we find that the state set proposed in the above section also satisfies the tri-tile structure. Takingd=3 as an example, it is obvious that thisC3?C3?C3system satisfies the tri-tile structure.

Proposition 2 If a 3-qudit UPB is strongly nonlocal,then the tripartite state set satisfies the tri-tile structure.

Proof A 3-qudit UPB with strong nonlocality cannot locally eliminate one or more state while performing nontrivial orthogonality-preserving measurement.Hence,all tiles should be irreducible in?A??B??CHilbert space.Therefore,this tripartite state set satisfies the tri-tile structure.

According to the definition of the tri-tile structure, we construct an incompleteC3×C3×C4system based on shift UPBs in Eq.(8),which is also strongly nonlocal. This system can lay the foundation for the further construction of 3-qudit UPBs with higher dimension.

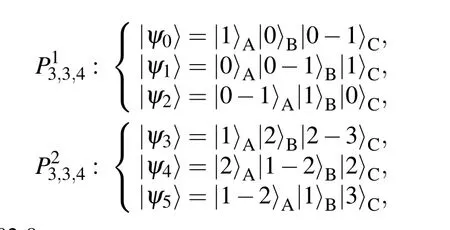
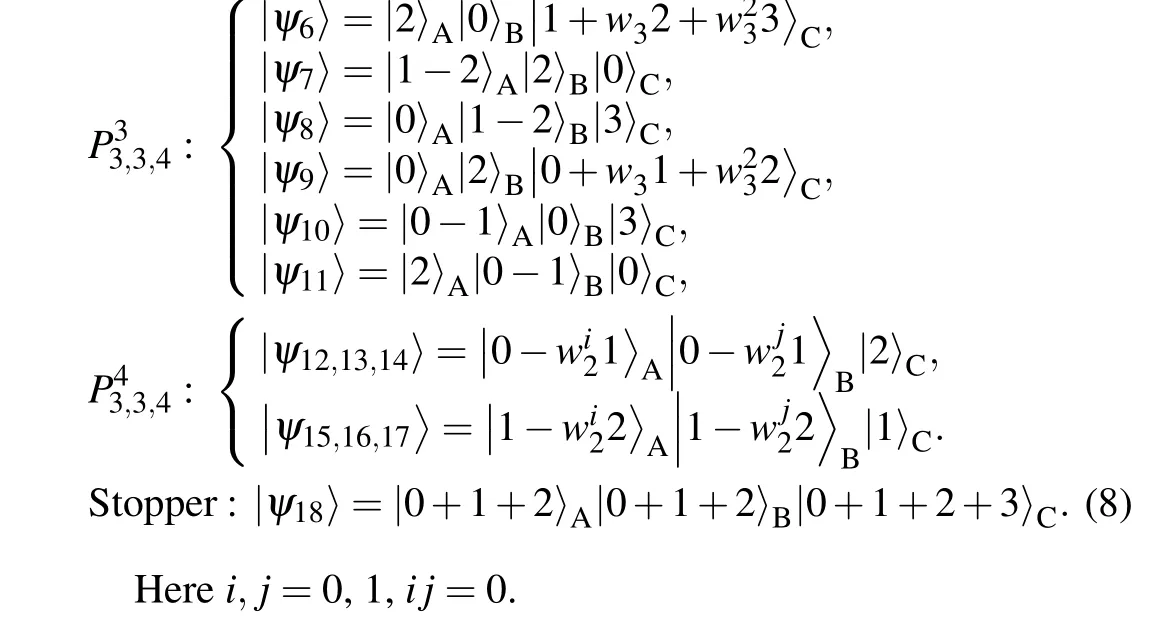
4.2. Construct aUPBin C4×C4×C5 system based on a UPB inC3×C3×C4 system

When constructing a UPB set of three parties with different dimensions, we adopt the similar practical method as before to construct high-dimensional state sets. Through verifying whether the constructed state set meets the tri-tile structure, we can judge whether the state set is strongly nonlocal more quickly and efficiently. Equation (9) is a set of incomplete UPBs inC4×C4×C5.

Fig.10. Composition of UPBs in C4 ?C4 ?C5.

4.3. Construct a UPB in Cd1 ?Cd2 ?Cd3 system based on a UPB in C(d1-1)?C(d2-1)?C(d3-1)system

Proposition 3: Let?A,?B,?Cbe Hilbert spaces of dimensiond1,d2,d3respectively. Suppose thatA={|1〉,...,|d1〉},B={|1〉,...,|d2〉},C={|1〉,...,|d3〉}are ordered orthonormal bases with respect to?A,?B,?C. InCd1?Cd2?Cd3,the set of UPBs given by Eq.(10)is pairwise orthogonal and strongly nonlocal.

Fig.11. Composition of UPBs in Cd1 ?Cd2 ?Cd3.

5. Conclusion

In summary, we have concentrated on the general construction method of 3-qudit UPBs exhibiting strong nonlocality. Firstly, a strongly nonlocal setC3?C3?C3of size 19 is constructed based on the shift UPBs. After a simple observation of its orthogonal graphs and corresponding 3×3×3 Rubik’s cube,the relationship among three qutrits is discussed and the structure of UPBs is analyzed. According to the above results, following the idea of deducing the UPBs with high dimension from the UPBs with low dimension,we try to construct UPBs with higher dimension and obtain a general set inCd ?Cd ?Cdof size (d-1)3+2d+5. Second, we extend the 2-qubit tile structure to 3-qudit and define it as a tri-tile structure,which is conducive for us to judge whether the state set is strongly nonlocal more quickly and efficiently. Based on this method, we give the construction process of 3-qudit UPBs with different dimensions. The construction of UPBs inCd1?Cd2?Cd3 is similar to that ofCd ?Cd ?Cdsystem,which also consists of four parts.

It is noted that the state set constructed using this general construction method includes a considerable number of states.Considering that reducing the number of quantum states is of great significance for exploring which states affect the nonlocality of the system, it is a valuable research direction to discuss the minimum number of states in 3-qudit UPBs. In addition,there is another kind of interesting state that is closely related to UPBs,BE states. It is also a worthy research direction to produce BE states of small rank by constructing UPBs.

Appendix A:Proof of Lemma 2

Lemma 2 InC4?C4?C4, the 3-qudit UPBs of size 40 given by Eq.(6)is strongly nonlocal.

Proof In order to make the proof process clearer, we first rewrite the original state, let|00〉 →|0〉,|01〉 →|1〉, ...,|33〉→|15〉. After rewriting the state in Eq.(6),we can obtain the following states:

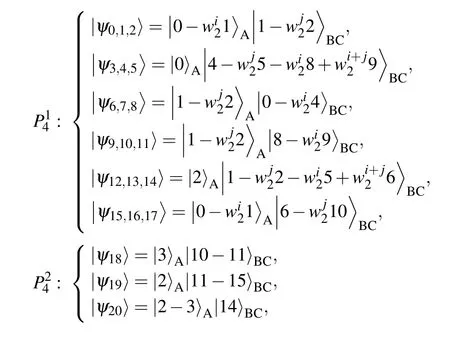
Suppose that theBCsystem starts with the nontrivial and non-disturbing measurement, represented by a set of POVM elementsM?mMmon 16×16 matrix. The POVM measurement in{|0〉,|1〉,···,|15〉}BCbasis corresponding to the states in Eq.(11),can be written as

Table 2 shows the detailed derivation process.

Obviously, theBC’s measurement matrix is proportional to the identity matrix, so it means that theBCsystem starts with a trivial measurement, and cannot get any information about shared state distinction from the measurement result.As for the other two division methods, i.e.,B|CAandC|AB, the proof method is similar to this. In summary, the multi-party divided into any two parts can keep the strong nonlocality of the quantum system.

Table 2. POVM elements.

Acknowledgements

This work was supported by the National Key R&D Program of China(Grant No.2020YFB1805405),the 111 Project(Grant No. B21049), the Foundation of Guizhou Provincial Key Laboratory of Public Big Data (Grant No. 2019BDKFJJ014),and the Fundamental Research Funds for the Central Universities(Grant Nos.2019XD-A02 and 2020RC38).