A GPU-based general numerical framework for plasma simulations in terms of microscopic kinetic equations with full collision terms

Junjie ZHANG (張俊杰), Xin ZHANG (張?chǎng)?, Guoliang PENG (彭國良),2 and Zeping REN (任澤平)

1 Northwest Institute of Nuclear Technology, Xi’an 710024, People’s Republic of China

2 College of Mechanical and Electrical Engineering, Beijing Institute of Technology, Beijing 100081,People’s Republic of China

Abstract We have proposed a general numerical framework for plasma simulations on graphics processing unit clusters based on microscopic kinetic equations with full collision terms.Our numerical algorithm consistently deals with both long-range(classical forces in the Vlasov term)and short-range (quantum processes in the collision term) interactions.Providing the relevant particle masses,charges and types(classical,fermionic or bosonic),as well as the external forces and the matrix elements(in the collisional integral),the algorithm consistently solves the coupled multi-particle kinetic equations.Currently,the framework is being tested and applied in the field of relativistic heavy-ion collisions; extensions to other plasma systems are straightforward.Our framework is a potential and competitive numerical platform for consistent plasma simulations.

Keywords: plasma simulations, GPU clusters, microscopic kinetic equations, Jefimenko’s equations, relativistic heavy-ion collisions, quark-gluon plasma

1.Introduction

1.1.Motivation

Plasma systems are of both theoretical and practical importance[1-5].The usual methods used to simulate plasma systems are magneto-hydrodynamic equations of conservation laws when the systems are in near-thermal equilibrium[6-8].However,there are many cases where the systems are far from thermal states, especially when particle production or chemical reaction processes are involved [9-11].In these highly non-thermal circumstances, one has to solve coupled Boltzmann-Maxwell equations instead.

The microscopic kinetic theory,i.e.the Boltzmann equation(BE)with full collision terms,is a widely used theoretical tool to describe the evolution of the system from non-equilibrium to thermal state [12-14].Providing proper configurations, the BE framework is able to give essential details of the momentum,spin, color and many other (microscopic) degrees of freedom.When coupled with external forces, such as electromagnetic(EM)and gravitational forces,the BE framework can be utilized to describe non-equilibrium plasma systems in a fully consistent way[15,16].For example,in a non-thermal plasma system,the charged particles scatter and generate EM fields in the medium.These EM fields will in turn affect the subsequent motions of these particles.A consistent way to take into account both the EM interactions and the particle scatterings is by using coupled Boltzmann-Maxwell equations:

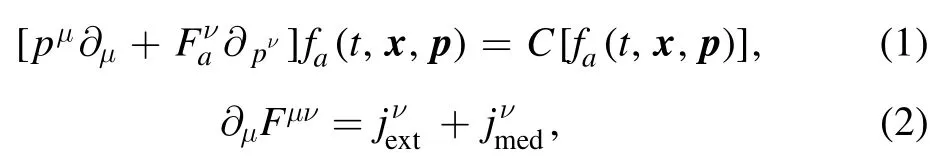
whereFμν= ?μAν- ?ν Aμis the EM tensor andfa(t,x,p)is the single particle distribution function for particle speciesawith chargeQa,C[fa(t,x,p)]is the collisional integral defnied in equation (11), and the four-momentum and four-current are denoted aspμandjν.The four-current for the interacting particles is given by

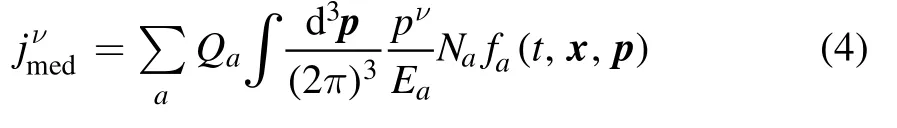
whereNais the microscopic degeneracy factor.For classical particlesNa=1.epresents the external four-current density,which should be provided separately.

Given the consistency for handling both the long-range interactions and the short-range scatterings, it is of both theoretical and practical importance to establish a general numerical framework for plasma simulations based on the microscopic kinetic equations with full collision terms.

1.2.Challenges for solving the coupled microscopic kinetic equations

Historically,consistently solving the six-dimensional coupled relativistic Boltzmann-Maxwell equations has always been a challenging task,even with the help of supercomputers with a few hundred petaflops [15, 16].

Consistently solving the coupled Boltzmann-Maxwell equations is difficult in various aspects.First, the full collisional integrals in BEs are high-dimensional[17-19].At each phase point, one needs to perform a numerical integration algorithm for the collision term.For 104time steps, we have to evaluate up to 1011integrations in total(e.g.the grid size of the phase space is206).Second, the Maxwell equations are numerically challenging on a spatial grid of size203(this size is mainly restricted by the BE on one Tesla V100 Card).The‘dilute’ grid density forces one to abandon the finite difference method for solving the Maxwell equations and to adopt an integral form of the retarded potential algorithm, which is resource-consuming [20].Third, the physical system is usually expanding(such as in relativistic heavy-ion collisions[21-23]).

The BE with full collisional integrals is a differentialintegral equation whose left-hand side involves differentiation in the six-dimensional phase space and the right-hand side involves an integration of the momentum space with up to nine dimensions for binary collisions.From the point of view of computational physics, neither side is easy to handle because of these large numerical dimensions.The toughest part of the full collisional BE is the high integration in momentum space (momentum integration is ‘non-local’ in terms of the momentum space).The ‘non-local’ property of the collisional integrals suggests that we should avoid dividing and distributing the momentum space on different cards.Thus, only the spatial domain can be divided onto different machines (nodes/cards).When we exchange the data in spatial boundaries, the corresponding three-dimensional momentum space should also be exchanged, making the exchanged data very large.Therefore, when solving the BE, we want to use as few nodes as possible.A graphics processing unit(GPU)card generally contains a few thousand parallel cores with each core having a clock rate a little less than 1 GHz, which is about 1/3-1/2 of a single central processing unit(CPU).From the estimation of the total clock rate, a GPU with 6000 cores (e.g.NVIDIA A100) is roughly equivalent to 60 CPUs(e.g.Intel i9-9960X).If we were to use CPUs, 60 CPUs usually require four nodes, compared with only one GPU card.This is the main reason that GPU is more suitable for BEs.

1.3.Microscopic kinetic equations on GPU clusters

With the state-of-the-art GPU [24, 25] clusters, a paradigm shift could be encountered.In this regard,we have designed a highly scalable framework to solve the coupled relativistic Boltzmann-Maxwell equations on multi-GPU clusters in Python language.Our aim is to handle the coupled equations with a certain level of accuracy for practical applications.The maximum capability of the grid resolution can reach approximately 106for quark-gluon plasma (QGP) systems and 206for classical plasma systems on one Tesla V100 card.For QGP systems, the algorithm takes around a day for a complete evolution on one Tesla V100 Card, and less consumption time is expected if a simpler form of the collision term is adopted (this is the case for non-relativistic systems)or if more GPU cards are involved.For practical applications,we have also designed several APIs for future development and implementation in other plasma systems.Our framework is a promising direction for first-principal plasma simulations on GPUs.

The paper is organized as follows.In section 2, we will briefly introduce the relevant equations and the proposed numerical framework based on our previous work with JefiGPU [26], ZMCintegral [27-29] and RBG [11].In section 3, we perform a toy model simulation that resembles parts of the AuAu collisions in the STAR experiments[30].In section 4, we conclude the current framework.

2.Numerical framework of the coupled relativistic Boltzmann-Maxwell equations

2.1.Theoretical set-up

To solve equations(5)-(8)numerically,we first express these coupled relativistic Boltzmann-Maxwell equations as follows:

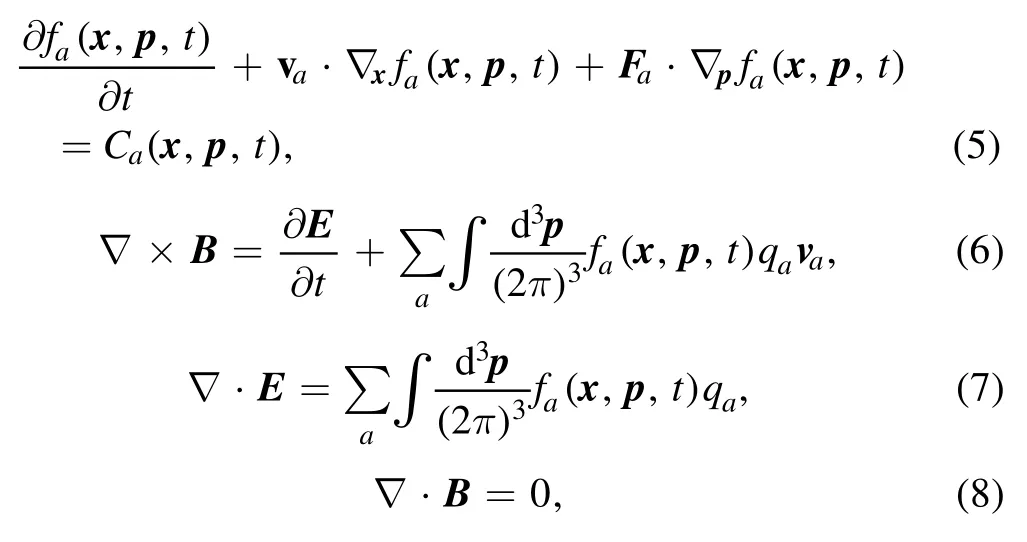
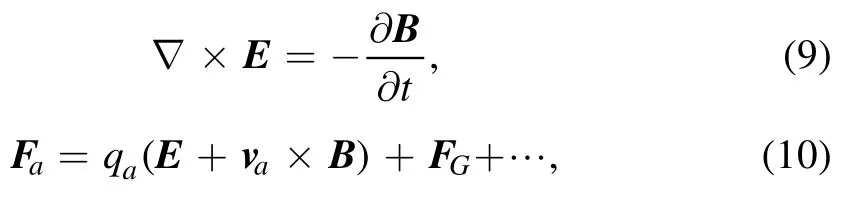
wherefa(x,p,t)is the phase space distribution function for particle speciesa,Eand B are the electric and magnetic fields in the laboratory frame,qais the electric charge carried by speciesa, andis the relativistic Lorentz factor defined by the drift velocityva.The external forcesFaacting upon the particles in the Vlasov term might involve EM interactions, gravitational interactions, etc.The collision termCa, which takes into account the short-range interactions of particle scatterings,is high-dimensional integrations of the form

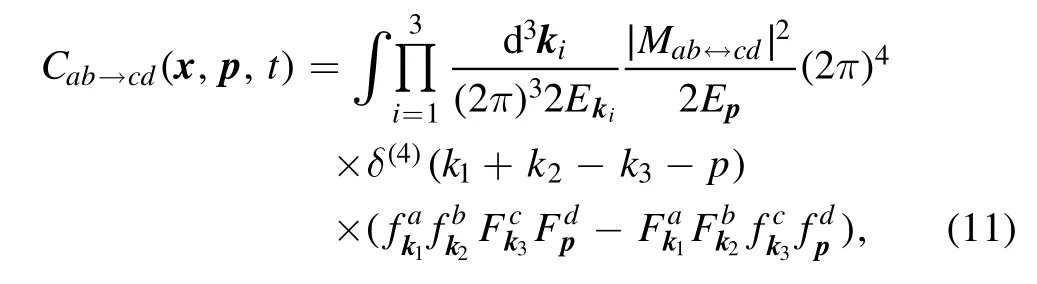
where the quantum corrections in the collision integral are defined asandThe invariant matrix elementMab?cdcan be directly obtained from the first-principal quantum calculations,e.g.for QGP, we use the tree-level Quantum Chromodynamics(QCD) calculations.

Note that the energy and momentum conservations for particle scatterings are guaranteed by the restrictionδ(4)(k1+k2-k3-p).For 2?2 scatterings (two incident particles and two outgoing particles)the particle numbers are always conserved, therefore

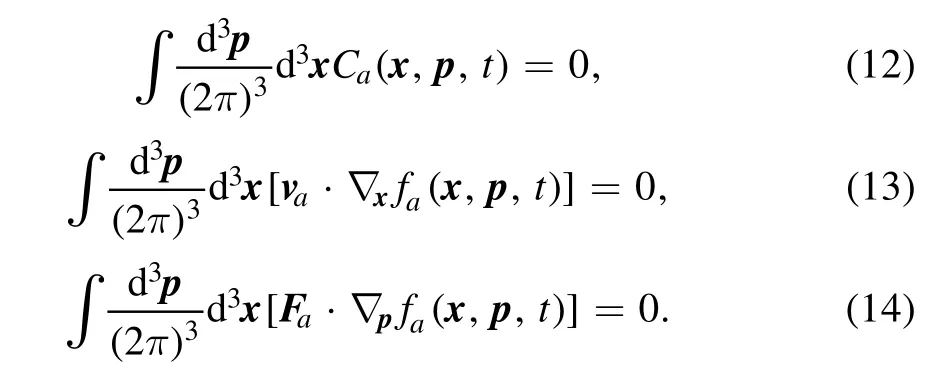
2.2.Numerical framework

The general structure of the RBG-Maxwell framework(relativistic BEs coupled to Maxwell equations on GPUs) is illustrated in figure 1.The framework contains three main modules: the external force (EF) module, the BE solver module and the EM solver module.When the physical system is in an external field such as the gravitational field, the EM field or any other ambient external field, the EF module will provide forces to the particles at all the time steps.The BE solver, after receiving the external forces, gives the new particle state in terms of particle scatterings.These particles,if carrying charges, will provide the electric sources to the EM solver.The framework is highly scalable on GPU clusters.

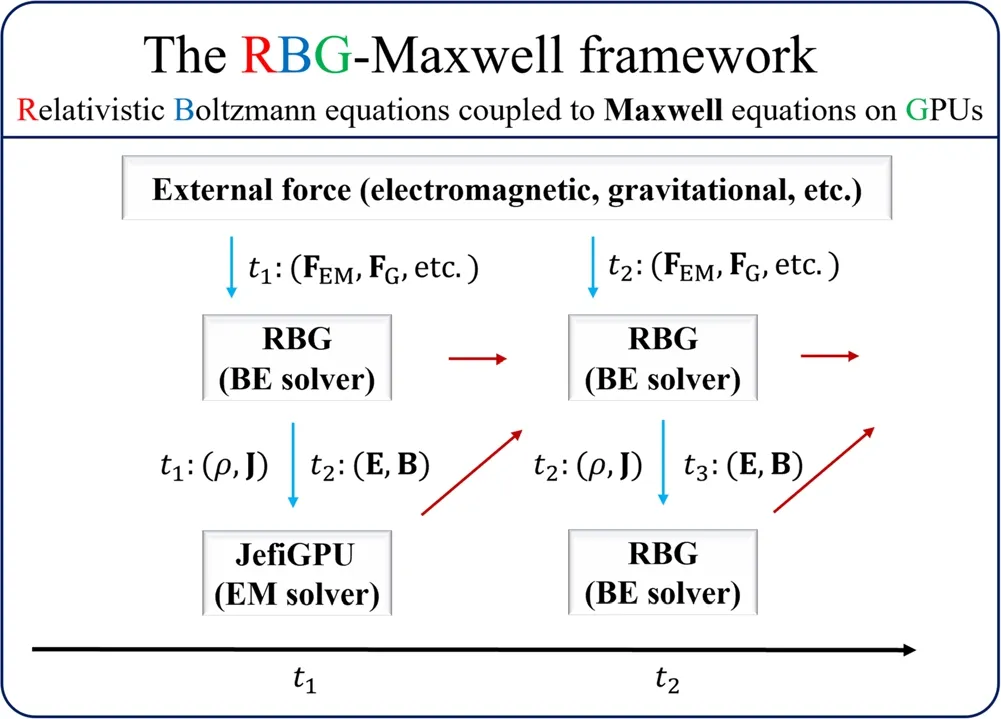
Figure 1.General structure of the RBG-Maxwell framework.The BE and EM solvers are revised from our previous packages JefiGPU(arXiv: 2104.05426) and RBG (arXiv: 1912.04457).At each time step, the BE solver provides the charge and current densities to the EM solver, which then gives the EM fields at the next time step.

The above framework is performed in Python with the Numba, Ray and Cupy packages with high scalability.For phase space size 106, time steps 104and seven particle species,it takes around a day for a complete evolution on one Tesla V100 card(the invariant matrix element takes the form of the tree-level QCD calculations).For classical systems with constant matrix element, the phase space size can reach up to206on one Tesla V100 card with a similar evaluation time (about a day).

In the current form, the framework contains collision terms of five-dimensional integrations involving seven particle species (u, d, s quarks, their anti-quarks and gluons).The direct Monte Carlo method is adopted to evaluate the collisional integral at each phase space point.Furthermore, since the BEs require a much smaller time step than the Maxwell equations, we have also used a stratified time step to balance the coupling of the BEs and the Maxwell equation for a stable numerical time evolution.For a strict particle number conservation in the collision terms, we have performed the symmetric sampling method mentioned in RBG [11], where the Monte Carlo integrations are evaluated by the CUDA atomic operation.The drifting and Vlasov terms are discretized by the usual upwind difference for numerical stability.The Maxwell equations are directly solved by JefiGPU[26], which is also scalable on GPU clusters.

Based on the previous work in [11] and [26], we have developed the RBG-Maxwell framework.Unlike in the previous implementations, we have made several essential changes in the RBG-Maxwell framework such that a stable and highly scalable simulation of the relativistic plasma is possible.

First of all,as an extension of[26],we have added highscaling functionality in the Jefimenko solver.The source regions and the observable regions are treated differently in the scaling procedure.On each GPU card we associate it with a rectangular spatial domain.The charged particles on the specific card (say card 0) generate the EM fields to all other observational regions on other GPU cards(say cards 1,2,and 3).At each time step,the plasma on card 0 generates the EM fields on cards 0, 1, 2 and 3.These EM fields are firstly obtained and saved on the GPU memory of card 0.Similarly,on card 2,we have EM fields on cards 0,1,2 and 3,etc.After the evaluation of the Jefimenko solver on all cards in parallel,the EM fields are exchanged across all GPU cards.Since the EM fields do not involve the momentum space, the exchanged data size is not large.

Figure 2.Evolution of the net charge density in the reaction plane.We can see that the partons are initially centered along z = 0.With the expansions of the partons, the densities decrease and eventually spread over a large region.

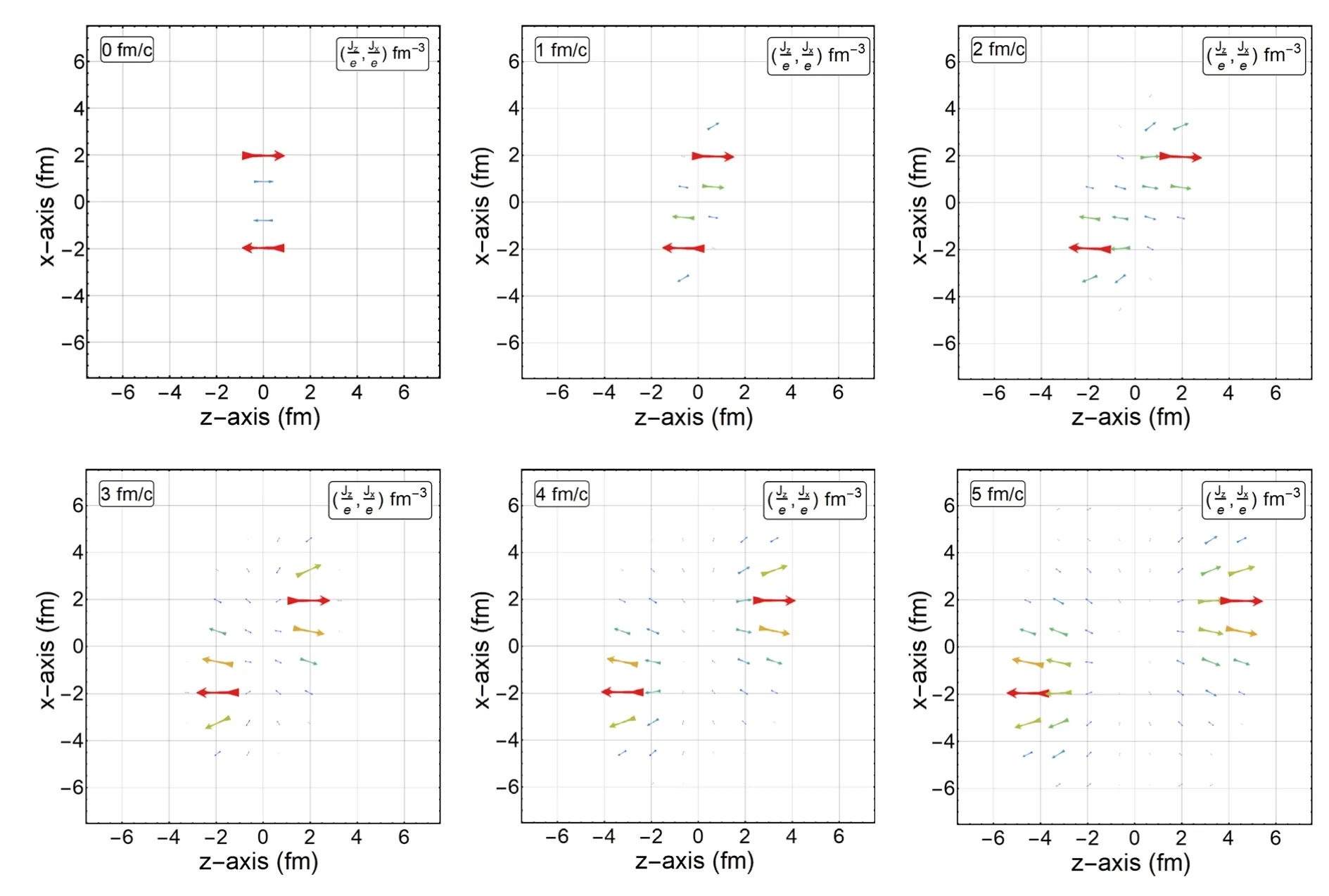
Figure 3.Evolution of the current density in the reaction plane.The currents initially point to the z-direction.With the pressure gradient and the EM interactions,the partons spread outward.Meanwhile,we also see the repulsion of the electric charges at x = 0 and z = 0 after 3 fm/c, which is consistent with that in figure 2.

Figure 4.Evolution of the EM field in the reaction plane.Since the partons are moving along the z-direction,the electric fields mainly point to the x-direction in the first few time steps.Electric fields from the spectator are initially pointing to the line of x = 0 due to the electric fields from the spectators.Along with the time evolution,the electric fields tend to point outward due to the charge repulsion from the participants.

Secondly,we have changed the strategy of the scaling in the BE.Since in[11]only a small number of spatial grids are used,the scaling of the BE is implemented via the distribution of sampling points in Monte Carlo integrations.In the RBGMaxwell framework, due to the relatively larger number of spatial grids and the non-local property of the momentum integrations, we divide the spatial domain onto different machines(nodes/cards),and exchange the data on the spatial ghost boundaries.In the usual computation, a GPU server contains up to 16 GPU cards, hence only 16 sub-domains in the spatial coordinate are used.Data exchange among 16 parallel cards is small compared with CPU-based clusters.

Finally,for a stable time-dependent evolution,we have to make sure that the distribution function always remains positive in each time step.In some time steps,the distribution function may be negative due to the updating.In these circumstances,we have to choose a small time step dt′ such that the updating of the distribution function is small.To perceive this functionality, we use the iteration relation dt′ = dt/n,wherenis a positive integer, dt′is the reduced time step,and dtis the initial used time step.This process is quite essential,otherwise the evolution will be extremely unstable.

3.Simulation of a toy model quark-gluon system

We have applied the RBG-Maxwell framework to the field of relativistic heavy-ion collisions.The simulation is performed in a system of seven particle species involving u,d,s quarks,their anti-quarks and gluons.The matrix elements in equation (11) can be found in [11].

The computational domain is restricted in a six-dimensional phase space of size [-6 fm, 6 fm] × [-7 fm, 7 fm] ×[-6 fm, 6 fm] × [-1.2 GeV, 1.2 GeV] × [-1.2 GeV,1.2 GeV] × [-2 GeV, 2 GeV] with grid sizes 41 × 1×41 × 19 × 5 ×39.The initial momentum condition is inspired by the CGC [31] scenario,

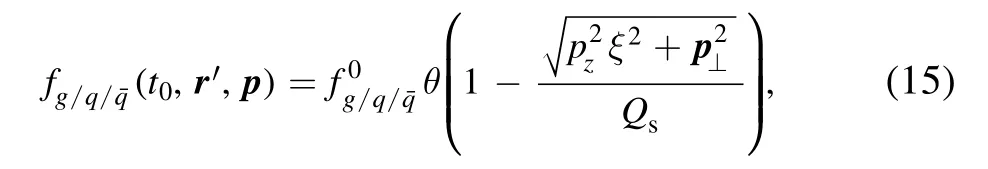
where the saturation scaleQs=1GeV [32] andt0～1/Qs～0.2fm/c [10, 33].We set the parameterξ= 1.4 [34] to introduce the anisotropy of the initial pressure.Note that equation(15)is defnied in the comoving frame whereis symmetric in terms ofpz.In heavy-ion collisions, different spatial pointsr′ in the overlapping region possess different initial net momentum,making the distribution,r′,p)asymmetric inpz.To apply equation(15), we first boost the region at pointsr′ to its comoving frame according to the net momentum; then, we sample the initial distribution following equation (15); finally, we boost the region back to the laboratory frame.The coefficients= 0.996?and= 1.14?,where the factor?～0.1 is chosen such that the total net charge of all partons in the rapidity range[-0.5,0.5]is consistent with the AMPT[35-37]calculations.?～ 0.1 indicates that only 10%of the particles in the overlapping regions are left to form the medium.The other 90% of particles in the overlapped region simply bypass one another and contribute to the decreasing background EM fields,denoted asin equation (6).The background EM fields generated by the spectators are obtained via the equations in[38] with impact parameterb= 8 fm.Hence,consists of two parts: one from the spectators and one generated by the particles that bypass one another in the overlapping regions.is the reciprocal of the coupling constant=3.33[39]andThe spatial boundary is taken to be the absorption boundary.The momentum boundary is chosen to have periodical boundary conditions since very few particles are present in the larger momentum grids.

Figures 2-4 depict the calculated results of the evolution of the charge densities, current densities and the induced EM fields in the reaction plane (xoz plane).

In the evolution of QGP, several stages are considered:pre-equilibrium, relativistic hydrodynamics and hadronization.By combining our framework with the hadronization process, we can calculate the charge-odd directed flowΔv,1which is the difference between the directed flows of charged particles and their anti-particles (one can refer to [40] for more details).In [40], the obtained results in the slopes ofv1andΔv1in mid-rapidity are in qualitative agreement with the STAR data,and the obtained electric and magnetic fields have opposite contributions tov1andΔv1but with the same magnitude.The results are insensitive to the values of the coupling constant and can be understood by a simple sum rule in a naive coalescence picture of hadronization.

4.Conclusion

We have proposed a general numerical framework for solving the coupled relativistic Boltzmann-Maxwell equations on GPU clusters.We have simulated a toy model quark-gluon system in relativistic heavy-ion collisions as an example to verify our code,and given the corresponding evolution of the charge and current densities as well as the induced EM fields.For a mimic of the STAR AuAu experiments using the RBGMaxwell framework, readers can refer to [40] for more details.More examples and accurate comparisons will be conducted in our future work.Our work is in principle equivalent to the PIC-MCC method, since in PIC-MCC, a consistent behavior of the particle scattering and the EM effects is also considered.However, our method is different from the PIC-MCC method in terms of the collision terms.In our method, we can simply adopt the cross-sections directly from the first-principal calculations, but for PIC-MCC it requires some sort of rescaling, which depends on the empirical analysis and experimental data.

Our work will be beneficial to various fields concerning the plasma system with full binary collisions.For instance,in the field of near-space plasma,hydron ions and oxygen atoms can collide and produce free electrons; these particles evolve under the influence of both the EM fields and the scatterings.In these conditions, the coupled Boltzmann-Maxwell equations can be of importance.Moreover, in system-generated EM pulses,the electrons are generated and moving in the atmosphere.In this process, collisions between electrons and air molecules are frequent,and hence require a self-consistent description of both the scatterings and the EM effects.

Acknowledgments

The authors are thankful for the technical support from Prof Qun Wang and Shi Pu from the University of Science and Technology of China and Xin-Li Sheng from the Central China Normal University.The work was supported by National Natural Science Foundation of China (No.12105227).

ORCID iDs