Nonlinear oscillation characteristics of magnetic microbubbles under acoustic and magnetic fields
Lixia Zhao(趙麗霞) Huimin Shi(史慧敏) Isaac Bello Jing Hu(胡靜)Chenghui Wang(王成會(huì)) and Runyang Mo(莫潤陽)
1Shaanxi Key Laboratory of Ultrasonics,School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710119,China 2Department of Chemistry,Ahmadu Bello University,Zaria 810001,Nigeria
Keywords: magnetic microbubbles,ultrasound,magnetic field,nonlinear oscillation
1. Introduction
Ultrasound contrast agents(UCAs)can not only improve the contrast of images,but also show great potential in molecular imaging and drug/gene delivery.[1]The use of ultrasound in combination with drug-loaded microbubbles offers considerable potential for the targeted treatment of a wide range of diseases including several types of cancer.[2]It is well known that UCAs are generally injected into the body through intravenous injections and delivered to the lesion site through blood circulation.[3]The extravasation of the drug during the circulatory delivery causes damage to other organs, and it is also not conducive for drug aggregation in the target area.[4]To achieve sufficient concentration at the targeted location,Zhanget al.[5]used drug-loaded microbubbles for targeted therapy and showed that antibody-targeted therapy effectively raise the inhibition rate of the tumor cellsin vivo. Microbubbles can also accumulate at the lesion site through the action of acoustic radiation force to achieve the purpose of treatment.[6]However,this method strongly depends on the conditions of blood flow and low concentration of microbubbles due to the blood flow will potentially decrease the targeting rate. To solve this problem, a potential strategy which has been demonstrated is to use microbubbles loaded with magnetics nanoparticles(MNPs)and form magnetic microbubbles(MMBs).[7]MMBs maintain the volume oscillation properties in moderate acoustic fields[8,9]and possess sensitivity to magnetic fields,whose location can be manipulated by an externally applied magnetic field. Magnetic field can weaken the strength of sonoluminescence in water under a fixed magnetic field,the sweep acoustic field results of Young[10]showed that the upper and lower bound of the forced pressure in the sonoluminescence region increased significantly with the magnetic field. The ability of MMBs to enhance the contrast of ultrasound/magnetic resonance images has been confirmed by many experiments.[11-14]The use of MMBs in therapeutic applications, in particular drug delivery and gene therapy has become a highly active area of research. Recently, Zhanget al.[15]utilized MMBs for ultrasound thrombolysis under a rotational magnetic field in different clot conditions and different clot ages(fresh,retracted)to improve the thrombolysis efficiency. Owenet al.[16]indicated that lipid-coated MMBs could be retained with a magnet against clinically relevant flow conditions. MMB can enhanc gene transfection has been demonstratedin vitroandin vivoby Stride.[2,14]However,the mechanisms of MMBs enhancement transfection rates are not clear. One hypothesis is that the external magnetic field causes a higher concentration of MMBs at the target site and ensures sufficient proximity between bubbles and target cells.[14]
In fact, the lack of a deep understanding of the dynamics of MMBs in the magneto-acoustic combined field has greatly limited their novel design and clinical application.[9]Further investigation to fully understand the mechanism of enhancement and, hence, optimize the delivery protocols is required. It is necessary to explore an innovation dynamic model and characterize the effects of MNPs on its dynamic and acoustic-magnetic responses of single MMB.Previous research has transformed the dynamics of MMBs into another problem: the dynamics of one or more non-magnetic bubbles within highly magnetic fluids.[17]Based on this approach,Malvaret al.[18]studied the dynamics of a spherical bubble in a magnetic fluid by a new version of the Rayleigh-Plesset equation, and pointed out that the bubble oscillatory motion can be controlled and its collapse can be avoided when a high magnetic is applied. The experiment data of external magnetic field modulation on bubble acoustic oscillation can be obtained by induction sensor and piezoelectric element,respectively.[19]Mulvanaet al.[20]modified the Church model[21]under the assumptions that the magnetic shell is a hydrophobic viscous fluid with uniformly distributed spherical magnetic nanoparticles,and the effects of the volume fraction of magnetic nanoparticles on the shell density was considered.Zhaoet al.[22]considered the influence of the volume fraction of MNPs on the viscosity of the fluid layer,and then analyzed the vibration behavior of MMBs only in the presence of an acoustic field.
The above alternative method,which treated single MMB as a nonmagnetic bubble in magnetic fluid, is indirect. In this work, a novel mathematical model is developed to study the dynamic behavior of a MMB under a combined magnetoacoustic field. A MMB is modelled as a air-filled sphere and surrounded by a double-layer membrane,which coupled with magnetic nanoparticles,and the influence of MNPs on the viscosity of magnetic fluid was considered. Furthermore,dimensionless parameters such as magnetic Reynolds number were used to make a dimensionless and linear analysis of the dynamic equation. The effects of magnetic physical parameters and acoustic parameters on the dynamics of the MMB was investigated to provide useful insights in previous studies.
2. Theoretical model
The structural model of a MMB is shown in Fig.1. The inner (1) is air and outer (3) is a hydrophobic phospholipid layer. The shell (2) is magnetic fluid layer (MFL) and it is consisted with hydrophobic oleic acid uniformly distributed with superparamagnetic iron oxide (SPIOs)nanoparticles. In previous reports, SPIOs were always used for incorporating MMBs and the sizes were generally from nanometers to tens of nanometers and then the MMBs would have a fast response to the external magnetic field.[9,11]The magnetic response of the MMB were affected by the volume fraction of SPIOs in magnetic fluid.[23,24]The initial inner and outer radius of the MMB areR10andR20,respectively. The thickness of layer(3)is much smaller than(2)and it is negligible. Both MF and the ambient liquid outside the bubble are incompressible Newtonian fluids and(ρs,ηs)and(ρl,ηl)are their density and viscosity, respectively. The viscosity of the phospholipid layer isηs0. The density of SPIOs particles isρnp, the volume fraction is generally less than 0.1[24]and the interaction between particles is negligible. The MMB was subjected to an combined external fields,which include a sine wave sound fieldpd(pd=pasin2π ft)and an applied magnetic field with intensityH. The magnetic field far from the bubble should approach the uniform field and the component in thezaxis isH0k.
This study is concerned primarily with the dynamic and acoustic-magnetic response of individual MMB.It is well accepted that US-induced stable and inertial cavitation plays an important role in the development of microbubble-assisted diagnostic and therapeutic application. However, it is very difficult to develop a mathematical model to describe nonspherical bubble due to the complexity responses in a combined magneto-acoustic field and more sophisticated numerical techniques. To simplify the problem, the effects of bubble translation under flow, acoustic radiation force or due to a magnetic field are neglected since these will occur on a relatively long timescale. Meanwhile, the non-spherical deformation of the vibrating bubble is ignored here. Assume that MMB only vibrates in the radial direction and remains spherical during expansion and contraction[25]and regardless of the mass exchange between the inside and outside of the membrane.




ThenHcan be written as



whereR10,Uc, andtcare characteristic length, velocity and time,respectively.The Reynolds numberReindicates the ratio of inertia force to viscous force,the Weber numberWedenotes the ratio of inertia force to surface tension and the magnetic Reynolds number,andRmagemeasures the ratio of inertia force to magnetic force. The relative permeability,μr, is given byμr=1+χ.
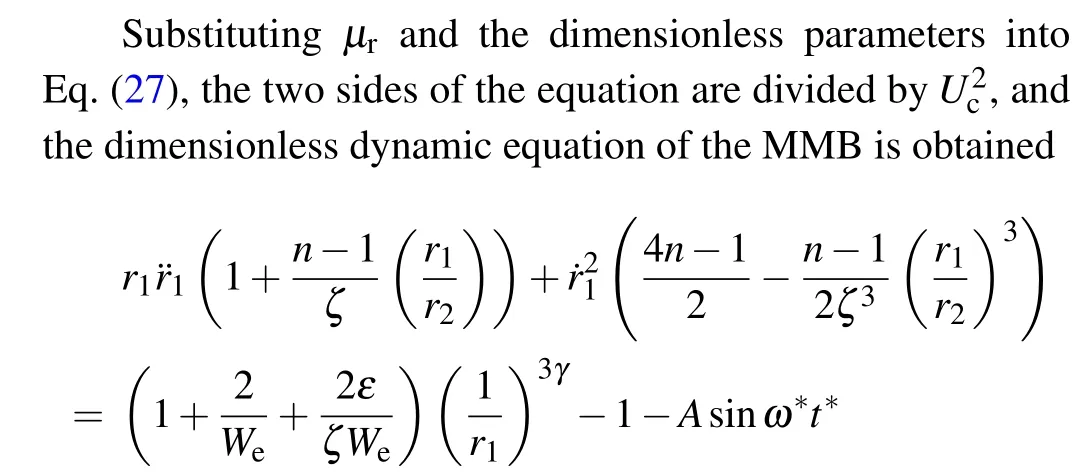

and
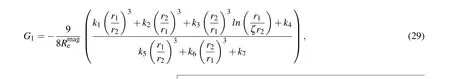

Substituting the dimensionless parameters into Eq. (31),the dimensionless equation is obtained only under the acoustic field
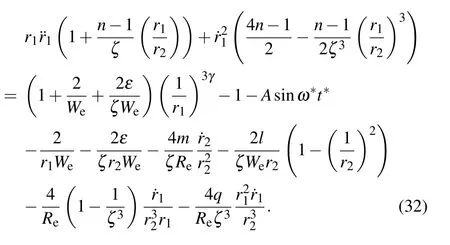
3. Numerical simulations
Numerical simulations performed in this section demonstrate the dynamics characteristics of MMB’s theoretical model. The simulations were carried out by using MATLAB.The parameters ofReandWewere presented in the reference of Malvaret al.[18]
3.1. Linear analysis
It was assumed that the amplitude of the MMB’s radial oscillation is small,therefore the inner and outer radius can be written as

Substituting Eqs.(33)and(36)into Eq.(28), linearizing it and retaining the first-order term ofδ(t),we can obtain the equation of the linear oscillator

where the dimensionless damping constantSand the dimensionless linear resonance frequencyω0are given by

where

It should be noted that in Eq.(39)ω0is related toQand magnetic Reynolds numberRmage,and it will be affected byH.To verify Eq.(39),it is substituted inRmage→∞and the result is


Fig. 2. Resonance frequency for an MMB as a function of radius ratio at different magnetic Reynolds number. (We =30, χ =1,Re =30,A=0.1,ω*=1).
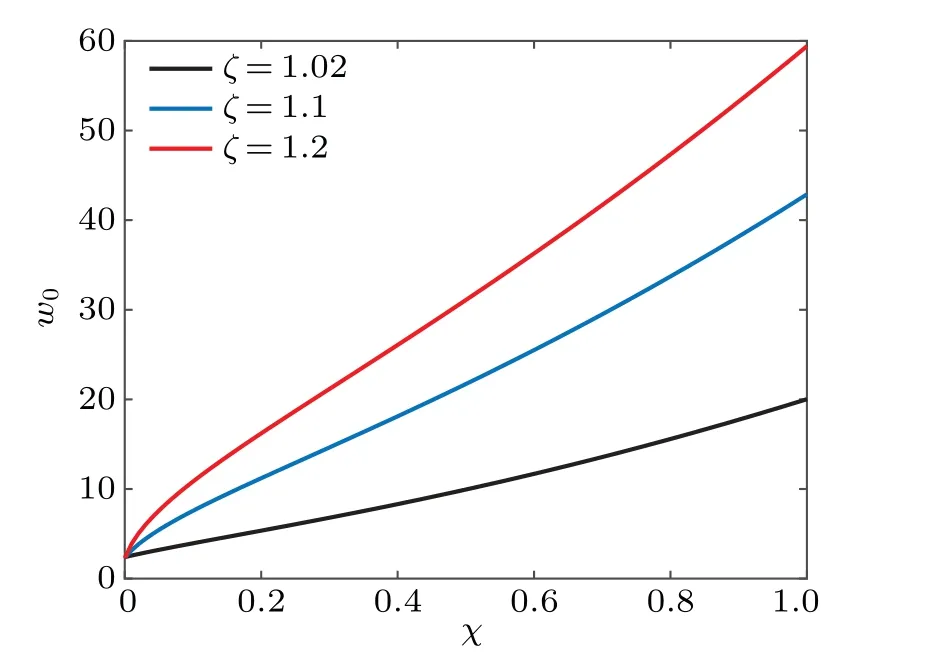
Fig. 3. Resonance frequency as a function of magnetic susceptibility.(Rmage =0.1,Re=30,We=30,ω*=1,A=0.1).
From Eq. (39), we can also find that the resonance frequency is affected byQand the magnetic susceptibilityχof the MF material. So the influence of susceptibility on the resonance frequency of MMB will be discussed below. Figure 3 shows that the resonance frequencyω0increases withχat three larger radius ratioζ(ζ=1.02, 1.1 and 1.2) when the MMB was subjected to a steady magnetic fieldRmage=0.1.This growth trend may be understood as that the higher magnetic susceptibility enhances the magnetic effect and produces a larger additional ambient pressure, and make the resonance frequency decrease. Significantly,for a fixedχ,ω0atζ=1.2 is higher thanζ=1.02 andζ=1.1. In this case,the magnetic field and magnetization susceptibility remain constant,a possible reason for the increase ofω0is that the effect caused by thickening is much less than that caused by magnetic pressure.
3.2. The effect of acoustic field and static magnetic field
3.2.1. Influence of Rmage
To understand how the static magnetic field affects the oscillation of the MMB,the influence of the non-dimensional parameterRmagewas calculated atA=0.1. Figure 4(a)shows the relationship ofr1-t*under differentRmage. The radial amplitude increases with the enhancement ofRmage. Nevertheless,a strongRmagemeans a weak magnetic field, so it can be said that the magnetic field retards both the expansion and contraction of the bubble. It was noted that the equilibrium radius of the oscillation also weakened asRmageincreases.

Fig.4. Vibration graph(a)and spectrogram of the radial oscillation(b)of MMB at Rmage =0.1,0.3,0.5,1.(ζ =1.2,A=0.1,Re=30,We=30,ω*=1).
To further understand how the intensity of magnetic field affects the stability and the nonlinear vibration of the MMB,it is important to analyze the frequency spectrum. Figure 4(b)shows that the resonance peak in fundamental frequency decreases as the intensity of field. There is a second harmonic andRmagedoes not affect the amplitude obviously. Only in a strong magnetic field, such asRmage= 0.1, the 5/2 ultraharmonic will be generated.These characteristics indicate that the existence of magnetic field suppresses the vibration of the MMB, and it is not completely stable. Malvaret al.[18]also observed a strong anisotropic effect on the radial oscillation of bubble in MFL and nonlinear effects caused by the unsteady expansion or contraction from transient cavitation. The amplitude is suppressed in a high-strength magnetic field,but the equilibrium radius of the microbubble would be enhanced.
The above analysis shows that the magnetic field suppresses the oscillation,so the vibration behaviors can be studied only in the presence of an external magnetic field.Figure 5 compares the vibration curves and equilibrium radius of the MMB atζ=1.02,1.1 and 1.2 in the same magnetic field. As a reference,the dotted line indicates the equilibrium radius in the absence of magnetic fluid. It can be seen that the magnetic field has little effect on the oscillation,and the equilibrium radius depends onζof the bubble. The results reveal that the bubble shows expansion and the subsequent damped oscillation whenζis relatively large, such asζ=1.2. On the contrary, the MMB has opposite behavior and collapses and the subsequent damped oscillation when the radius ratio is small,such asζ=1.02 and 1.1. The subsequent damped oscillation also verifies that the magnetic field can make the oscillation more stable. Simultaneously,with increasing radius ratio,the equilibrium radius increases.

Fig.5. Variation of radius with time in response to different ζ without the sound field(A=0,Rmage =0.1,Re=30,We=30,ω*=1).
The magnetic field deviates the equilibrium radius of the microbubble. There is no driving sound field, the magnetic field acts as damping to affect its oscillation characteristics,and the phase diagrams are shown in Fig.6. As the energy is consumed,the amplitude of the vibrating microbubble gradually decreases. Besides, the phase trajectory is a non-closed curve and the vector diameter is a logarithmic decay. After several rotations from the starting point, the phase trajectory will tend to the center point where the equilibrium radius is located and the point is an attractor. A possible reason for the opposite direction of oscillation is that the magnetic pressure is not enough to offset the inertia pressure.[18]In fact,the MMB vibrate under the combined action of magnetic pressure and inertial pressure, and they compete with each other. If the magnetic pressure is dominant,the vibration is restrained,otherwise it is strengthened.[23]

Fig.6. MMB phase diagram in the magnetic field at ζ =1.02,1.1,and 1.2. (A=0,Rmage =0.1,Re=30,We=30,ω*=1).
3.2.2. Influence of χ
The response of a magnetic material to an applied magnetic field is the magnetization behavior, which is generally characterized by its susceptibility.The spins of MNPs produce magnetization and change the arrangement direction, which affects their magnetic properties under the magnetic field.
Figure 7(a) demonstrates the oscillation of the MMB at three values of susceptibility. As can be seen, the maximum and minimum amplitudes are the smallest among the three sets of comparisons whenχ=0.1,while they are the largest whenχ=0.5. Asχincreases to 1, the amplitude decreases again.At the same time,the values ofχare smaller,contributing to a decrease of equilibrium radius. The dynamic behavior may be caused by the different number of magnetic particles arranged in the direction of the magnetic field in the MFL,which leads to changes in vibration mode under the microscopic mechanism.

Fig.7. Vibration graph(a)and spectrogram of the radial oscillation of MMB (b) at χ =0.1, 0.5, 1. (ζ =1.2, A=0.1, Re =30, We =30,ω*=1,Rmage =0.1).
To further discuss the influence of the magnetic susceptibility on the radial oscillation, spectrum analysis was performed in Fig. 7(b). It shows that as the magnetic susceptibilityχincreases, the resonant amplitude decreases. That is to say, the increase of magnetic susceptibility inhibits the vibration. Essentially,MMB dynamics are highly dependent on the magnetic susceptibility difference between the shell material and ambient fluid. In this work,except for the material of MFL,other media are assumed to have no magnetic response and the susceptibility values were ignored. It is strictly regulated thatχused in this work is the difference of MF and surrounding medium. The result shows that the 2 and 12/5 ultra-harmonic are produced in this three cases. The second harmonic amplitude also decreases whenχincreases and the largest amplitude of the 12/5 ultra-harmonic is atχ=0.5.The effect of magnetic susceptibility on nonlinear behavior is very weak.
3.3. Effect of the acoustic field
3.3.1. Influence of acoustic pressure
When the applied acoustic field parameters are unlike,the dynamic response of the MMB is also different. Figure 8 shows the behavior of the radius as a function of acoustic pressure for different values ofA(0.1,0.5,1 and 1.5). It was noted that higher values of acoustic pressure increase the oscillation values of the radius and the unstable oscillations in the peak corresponding area becomes more obvious. In other words,greater acoustic pressure leads to the instability of the magnetic microbubble oscillation. Under acoustic waves of different intensities, although the oscillation follows the same mechanical laws,their vibration behavior is variable.
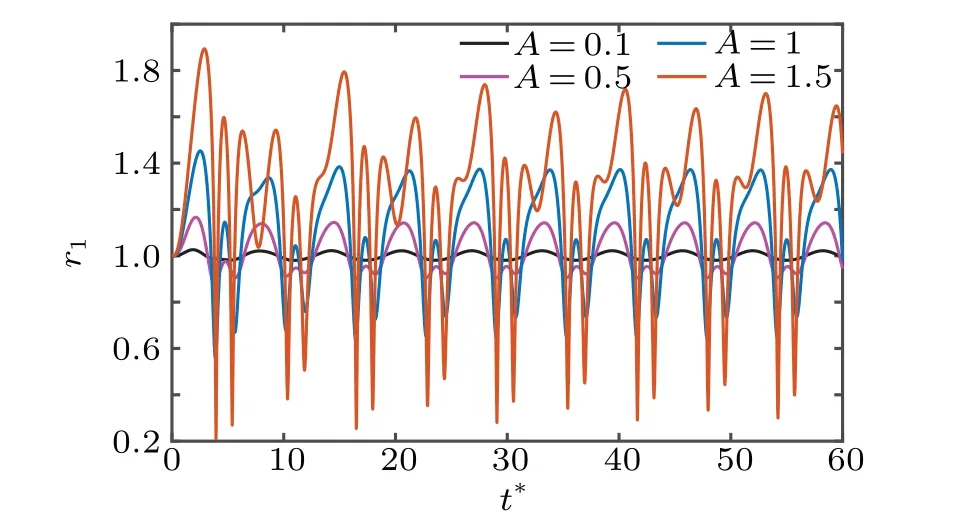
Fig.8. The effect of acoustic pressure on MMB’s vibration. (ζ =1.02,Re=10,We=20,ω*=1,Rmage =1).
To observe the unstable response of radius oscillation under higher acoustic pressure values, the phase diagram-Poincar′e cross-section diagram was taken for further analysis,as shown in Fig.9. It shows that as the amplitude of acoustic pressure increases, the trajectory appears as numerous closed trajectories,and the shape of the trajectories is distorted from an elliptical shape. The more closed the trajectories of the microbubble,the more obvious the distortion,which indicates that the higher the energy contained and the stronger nonlinearity of the oscillation. Correspondingly, the points of the trajectory passing through the Poincar′e cross-section increases from the finite point set to the infinite point set.

Fig. 9. The phase diagram and Poincar′e cross-section (red dots) of MMB at(a)A=0.1,(b)A=0.5,(c)A=1,(d)A=1.5.
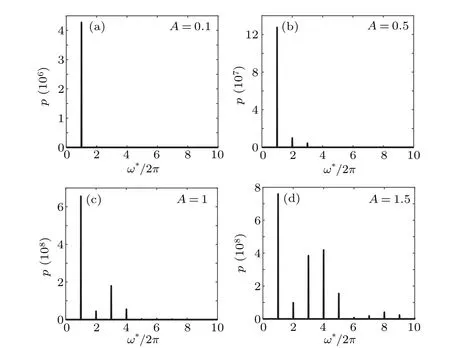
Fig.10. The spectrum diagram of MMB at(a)A=0.1,(b)A=0.5,(c)A=1,(d)A=1.5.
Figure 10 shows the power spectrum obtained after the Fourier transform of the radius oscillation under four values of acoustic pressures. The harmonic component in the power spectrum is a sign of cavitation occurrence. As the pressure of the acoustic field increases, the resonant amplitude of fundamental frequency increases and the harmonic components increases as well.That is,when the intensity of the acoustic field is higher,the MMB absorbs more acoustic wave energy during the oscillation process,which is more conducive to cavitation.The harmonic components tend to increase with higher acoustic pressure and this means that the radius oscillation process presents stronger nonlinear vibration characteristics.
3.3.2. Influence of driving acoustic frequency
The frequency of the driving acoustic field is also an important parameter of microbubble oscillation. In Fig.11,it is possible to show that the radiusr1changes with normalization timet*at four values of the acoustic frequencies tested. When other parameters remain fixed, as the acoustic frequencyω*increases,the maximum amplitude of the transient and steadystate response radius tends to decrease. In other words, high acoustic frequency has stronger suppression on the bubble radius. To further understand how the acoustic frequency affects the radius stability,it is significant to discuss the phase space at different frequencies.As shown in Fig.12,the most obvious phase diagram distortion occurs at the minimum acoustic frequency, and the radial amplitude and wall velocity both have the largest value. However, a higher acoustic frequency will lead a more steady oscillation state in steady-state response and nonlinear oscillation state during its transient response,respectively. Thus,the MMB has an opposite response to lowfrequency and high-frequency acoustic fields such that highfrequency avoid collapse. It can be seen from Fig.12 that the Poincar′e cross-section points on the outer trajectory increase,while the points on the internal phase trajectory are concentrated,showing relative stabilization.

Fig. 11. The effect of acoustic frequency on radius oscillation. (ζ =1.02,Re=10,We=20,A=1.5,Rmage =1).
Figure 13 shows the power spectrum of the oscillation at four frequencies of the acoustic field. It was noted that increasing the frequency of the acoustic field reduces the ultraharmonic and increases the subharmonic components. It was observed that the radius oscillation stabilizes gradually, and the nonlinearity of the steady-state weakens.

Fig.12. The phase plot and Poincar′e cross-section(red dots)of MMB at(a)ω*=2,(b)ω*=5,(c)ω*=10.
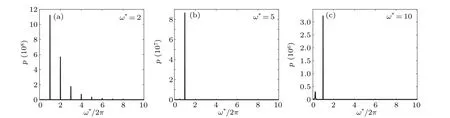
Fig.13. The spectrum diagram of MMB at(a)ω*=2,(b)ω*=5,(c)ω*=10.
3.4. The effects of the oscillatory magnetic field
Considering that the magnetic field is related to the time variable, its influence on the vibration characteristics of the microbubble is different from the steady static magnetic field.In this section, we will discuss the effects of changing magnetic field on the dynamic behavior of MMB.
3.4.1. Influence of magnetic frequency
The effects of the steady and time-varying magnetic field on the radius oscillation were studied. To explore how the combination of static and oscillating magnetic fields affects the radius oscillation, the relationship ofr1with timet*at three values ofωmwas studied and the results are shown in Fig. 14. Whenωmincreases from 1 to 3, the amplitude has barely changed, but the vibration curves are more disorganized. The oscillation tends to be stabilized atωm=5 and the amplitude is minimal at this case. It is known that the higher the frequency of magnetic field is, the more stable the MMB vibration is.
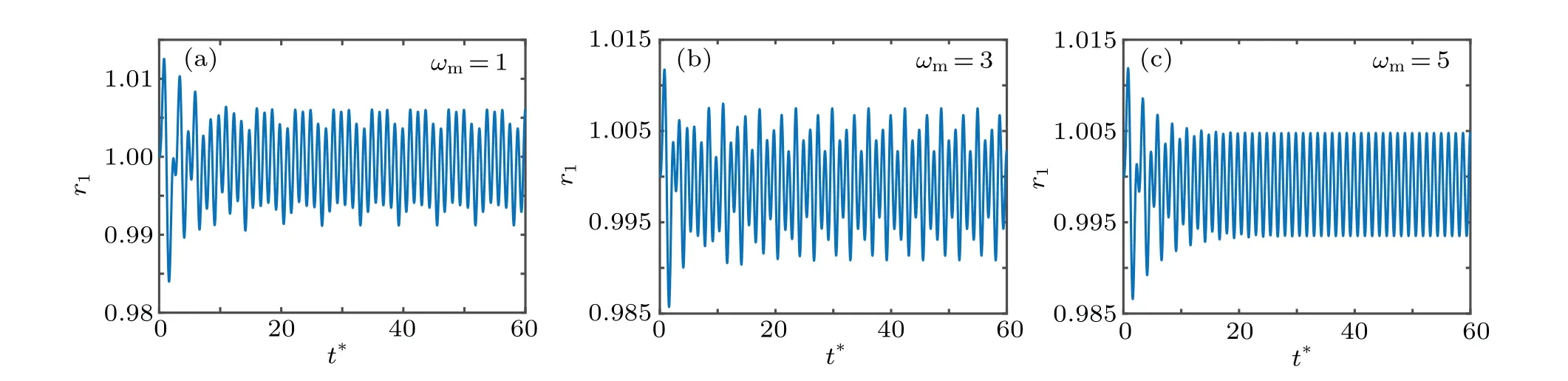
Fig.14. The effect of ωm on radius oscillation at ωm=1,3,5. (ω*=5,ζ =1.02,Re=10,We=20,A=0.1,Rmage =1).
In this section, the nonlinear effects of MMB to a timevarying magnetic field comes into focus. In Fig.15,the nonlinear effects of oscillating magnetic field on oscillation is more marked than a steady one. The phase trajectory is limited to a certain area,showing integral stability and local instability. The points on the Poincar′e section are more scattered whenωm=3,which is seen in Fig.15(b). It can also be seen in Fig.16(b)that the value corresponding to the subharmonic component becomes larger. There is also a subharmonic component whenωm=1 (Fig. 16(a)), but its amplitude is very small. Whenωm= 5 (Fig. 15(c)), the phase trajectory becomes a stable limit circle. The Poincar′e cross-section points gather together,forming a line. In Fig.16(c),there is only the fundamental frequency which implies that the magnetic microbubble does a stable periodic oscillation at this time without cavitation.
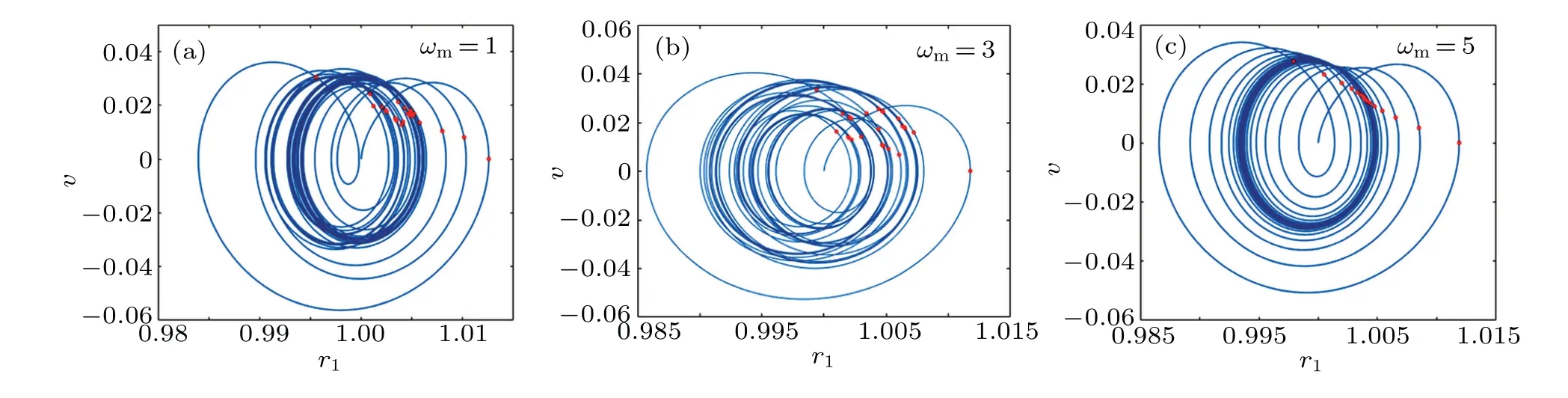
Fig.15. The phase plot and Poincar′e cross-section(red dots)of MMB at ωm=1,3,5.

Fig.16. The influence of different ωm on radius oscillation at ωm=1,3,5.
3.4.2. Influence of acoustic frequency
To research whether the influence of the oscillating magnetic field on radius oscillation is related to the acoustic field,the relation betweenr1andt*is shown in Fig. 17, which is compared with the sameωmin Fig. 14. It can be seen that the amplitude also goes up and then goes down, and reaches the maximum atωm=3. However, the oscillation pattern is disordered and different from that in the static magnetic field.The phase trajectory shown in Fig.18 tends to be out of order with the increase of the acoustic frequency,and the amplitude and bubble wall velocity both decrease.The points in Poincar′e section are randomly distributed, showing stronger nonlinear oscillation characteristics. Comparing the three cases of different magnetic field frequencies in Fig.18, asωmincreases,the phase trajectories first disperses in a certain area and then gather inward, showing a stable state. Yet, the transient response shows more nonlinearity. The points on Poincar′e section change from disorder to relatively orderly arrangement.Whenωmincreases to 5, the points are distributed closer to the center.

Fig.17. The effect of ωm on radius oscillation when ω*=10.
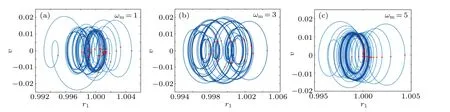
Fig.18. The phase plot and Poincar′e cross-section(red dots)of MMB at ωm=1,3,5.

Fig.19. The spectrum diagram of MMB at ωm=1,3,5 when ω*=10.
Compared to the power spectrums in Fig. 16, it can be seen in Fig. 19 that there are more subharmonic components when the frequency of the acoustic fieldω*is higher. Figure 19(a)shows that there are 1/10, 1/5 and 1/4 subharmonic components and the amplitude of 1/10 subharmonic is 1.13 times larger than the fundamental frequency whenωm=1. In the case ofωm=3 in Fig. 19(b), there is only a 3/10 subharmonic frequency, and the amplitude of subharmonic frequency is 4.19 times larger than the fundamental frequency.In Fig.19(c),there are 1/4 and 1/2 subharmonic components,and the corresponding amplitudes of the subharmonic frequencies are 0.076 and 0.1 times of the fundamental frequency,respectively.Figure 19 illustrates the spectrum diagram of radial oscillation at three values ofωm(1, 3 and 5). The amplitude of the fundamental frequency increases slightly whenωm=3 and then decreases whenωmincreases to 5.
4. Conclusions
Considering the magnetic field contribution on the mechanical properties of the shell,the dynamic characteristics of MMB in a viscous fluid under acoustic and magnetic fields was investigated. An improved version of the Rayleigh-Plesset equation was formulated by considering the magnetic effects of the multi-layer microbubble dynamics. It was noted that the strength of the steady magnetic field intensity increased the resonance frequency and equilibrium radius.However, magnetic field suppressed the MMB’s oscillation and generated a harmonic response. The susceptibility of the magnetic material of MFL was also high enough, the resonance frequency increased and the oscillation was suppressed. The MMB vibrated under magnetic field damping and amplitude attenuation, and the equilibrium radius was related to the radius ratio.Whenζwas relatively small,the equilibrium radius was less than 1,while it was greater than 1 whenζwas large.When the acoustic pressure was higher, the oscillation was much more violent,the points passing through Poincar′e crosssection and the doubled frequency components increased,and then the nonlinear characteristics were stronger.
On exploring the influence of magnetic field frequency on the vibration of the microbubble under different acoustic field,if the applied magnetic field changes with time,the influence of an time-varying magnetic field on the radius was related to the acoustic frequency. Increasing the acoustic frequency suppresses the amplitude and the velocity of the bubble wall. The transient nonlinearity response increases while that of steadystate response weakens. Furthermore, the variation of magnetic field frequency affects the vibration state and nonlinear vibration characteristics. As the frequency of the magnetic field increases,the amplitude of radius first increases and then decreases,and its subharmonic components reduce.
Acknowledgement
The authors acknowledge the support of the National Natural Science Foundation of China (Grant Nos. 12074238 and 11974232).
- Chinese Physics B的其它文章
- Surface modulation of halide perovskite films for efficient and stable solar cells
- Graphene-based heterojunction for enhanced photodetectors
- Lithium ion batteries cathode material: V2O5
- A review on 3d transition metal dilute magnetic REIn3 intermetallic compounds
- Charge transfer modification of inverted planar perovskite solar cells by NiOx/Sr:NiOx bilayer hole transport layer
- A low-cost invasive microwave ablation antenna with a directional heating pattern

