Non-Hermitian quasicrystal in dimerized lattices?

Longwen Zhou(周龍文) and Wenqian Han(韓雯岍)

College of Physics and Optoelectronic Engineering,Ocean University of China,Qingdao 266100,China

Keywords: non-Hermitian system,quasicrystal,localization,topological phase

1. Introduction

Quasicrystals have long-range order without spatial periodicity. They form a class of system in between crystals and fully disordered lattices.[1–6]Experimentally, quasicrystals have been realized in a variety of solid state materials and quantum simulators.[7–13]Rich phenomena induced by quasiperiodicity have been revealed, such as topological phases,[14–21]quantized adiabatic pumping,[15,20,21]anomalous transport and localization transitions,[22–51]attracting attention over a broad range of research fields.

Recently, the study of quasicrystals has been extended to non-Hermitian systems, where the interplay between quasiperiodicity and gain/loss or nonreciprocity could induce exotic dynamical, localization and topological phenomena.[52–69]In particular, in non-Hermitian variants of the Aubry–Andr′e–Harper (AAH) model, complex onsite potential or nonreciprocal hopping could induce aPT-breaking transition and a metal–insulator transition, which can be further characterized by a spectral topological winding number.[52,56]In related studies, non-Hermiticity induced mobility edges in generalized and superconducting AAH models have also been found and described by topological invariants.[54,57–59,62,67]Besides,the investigation of wavepacket spreading in non-Hermitian quasicrystals (NHQCs) has revealed their anomalous dynamical features,[55,60]such as the disordered-enhanced transport.[55]

Meanwhile, the Su–Schrieffer–Heeger (SSH) model[70]provides another paradigm for the study of localization,[71]topological[72]and non-Hermitian[73–75]physics. Specially,the hopping dimerization allows the SSH model to possess a topological phase characterized by an integer winding number and degenerate edge modes.[72]However, in the context of non-Hermitian quasicrystals, phases and phenomena that could arise due to the interplay between spatial aperiodicity and hopping dimerization have not been revealed. In this paper, we address this issue by introducing a dimerized quasiperiodic lattice in Section 2, which forms a hybridization of the SSH and non-Hermitian AAH models. The system is found to possess rich patterns ofPT-breaking and localization transitions,together with three phases of distinct transport nature. In Section 3,we perform detailed analyses of the spectrum and localization nature of these phases, and construct a pair of topological winding numbers to characterize the transitions between them. Despite an extended and a localized phase, we also find a mobility edge phase, which is absent without the hopping dimerization. These discoveries thus uncover the richness of topological and transport phenomena in dimerized NHQCs. In Section 4, we summarize our results and discuss potential future directions. Further details about the spectrum,Lyapunov exponents and wavepacket dynamics are provided in the Appendix.

2. Model

In this section, we introduce the dimerized NHQC that will be investigated in this work. Our model can be viewed as an extension of the AAH model,[5,6]which is prototypical in the study of localization transitions in one-dimensional (1D) quasicrystals. In position representation, the Hamiltonian of the AAH model is ?HAAH= ∑n(J|n〉〈n+1|+H.c.+Vcos(2παn+λ)|n〉〈n|),where{|n〉}represents the eigenbasis of the lattice,Jis the hopping amplitude,Vcontrols the strength of the onsite potential, andλis a phase shift. Whenαis irrational, the potentialVn=Vcos(2παn+λ)is quasiperiodic inn,and ?HAAHdescribes a 1D quasicrystal. WhenV<2J, the spectrum of ?HAAHis continuous and all its eigenstates are extended under the periodic boundary condition(PBC).Comparatively, ?HAAHpossesses a point spectrum with localized eigenstates at all energies whenV>2J. WhenV=2J, the spectrum of ?HAAHis purely singular continuous with critical wavefunctions,and the system undergoes a localization transition whenVchanges fromV<2JtoV>2J.[4]

Recently, a non-Hermitian variant of ?HAAHwas introduced by settingλ=β+iγ, with (β,γ)∈R.[52]Such a non-Hermitian AAH model possessesPT-breaking and localization transitions atγc=ln(2J/V), which are accompanied by the quantized jump of a spectral winding numberw.Forγ<γc(γ>γc),the spectrum is real(complex)with winding numberw=0(w=?1),and each eigenstate is extended(localized).[52]Since all states subject to the same localization transition atγ=γc, no mobility edges are found. Similar results were reported in a nonreciprocal AAH model,[56]which might be related to the model in Ref.[52]by Fourier transformations.

Fig.1. Schematic illustration of the dimerized NHQC. Solid balls denote lattice sites with index n ∈Z. Hopping amplitudes are alternated between J ?Δ (solid lines)and J+Δ (dashed lines). Vn represents the strength of the onsite potential,with irrational modulation parameter α and phase shift iγ.

In this work, we consider another extension of the AAH quasicrystal by introducing hopping dimerizations. We setJ →Jn=J+(?1)nΔas the hopping amplitude between then’s and the(n+1)’s lattice sites,and letλ=iγbe the imaginary phase shift in the onsite potentialVn. Our model Hamiltonian thus takes the form

A schematic illustration of the model is shown in Fig.1.WhenV=0,Eq.(1)reduces to the SSH model with hopping dimerizationΔ. WithV,γ/= 0, ?Hdescribes an SSH chain with quasiperiodically correlated non-Hermitian disorder. Therefore, our system realizes a hybridization between the AAH and SSH models. Since the realizations of SSH and non-Hermitian AAH models have both been discussed,[52,76]we expect our model to be within reach under current or near term experimental conditions. Furthermore, our construction allows us to explore the interplay between hopping dimerizations and quasiperiodic non-Hermitian potential,which could lead to rich phase diagrams and transport phenomena,as will be shown in the following section.

3. Results

3.1. Spectrum and level statistics

The spectrum of the dimerized NHQC is obtained by solving the eigenvalue equation ?H|ψ〉=E|ψ〉. Projecting the equation to the lattice representation,we find

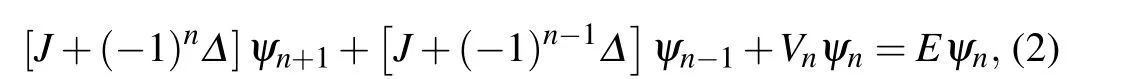
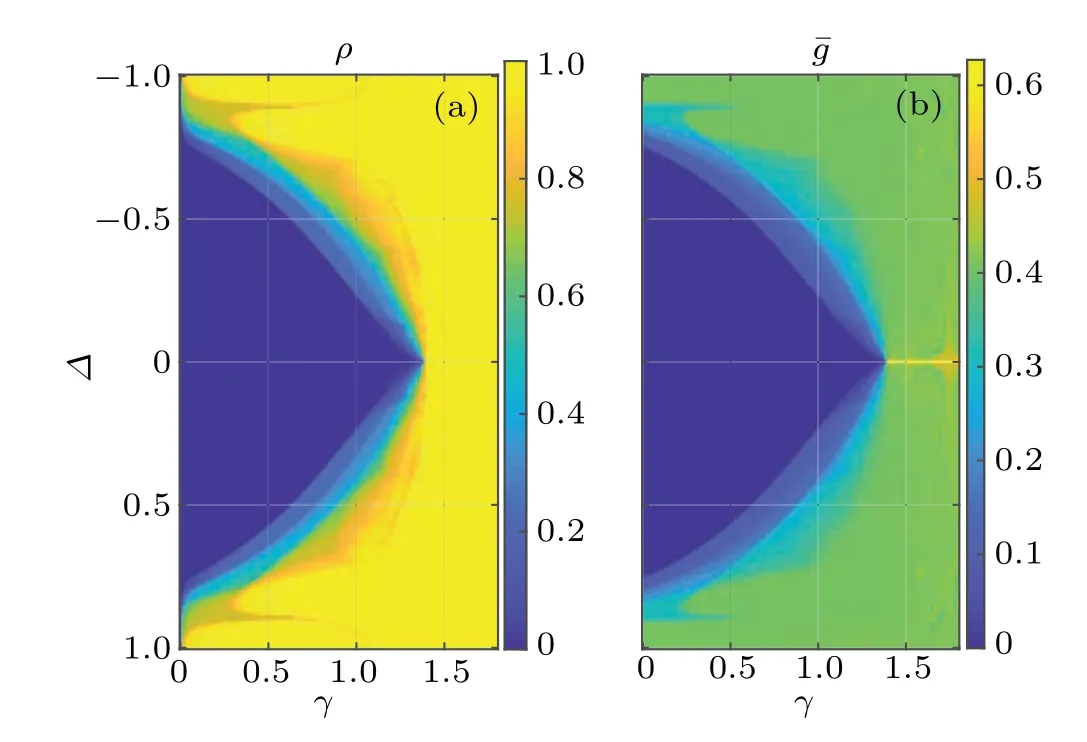
Fig.2. (a)Density of states with complex eigenvalues and(b)averaged AGRs of ?H versus the dimerization amplitude Δ and the imaginary part of phase shift γ. System parameters are set as J =1, V =0.5, and. PBC is taken in the calculation and the length of the lattice is L=2584.

To have a comprehensive view of the spectrum and its connection with localization properties of states, we present the density of states with nonzero imaginary parts of energies and the mean of AGRs versusγandΔin Figs.2(a)and 2(b),respectively. The density of states with complex energies is defined as

3.2. Inverse participation ratio

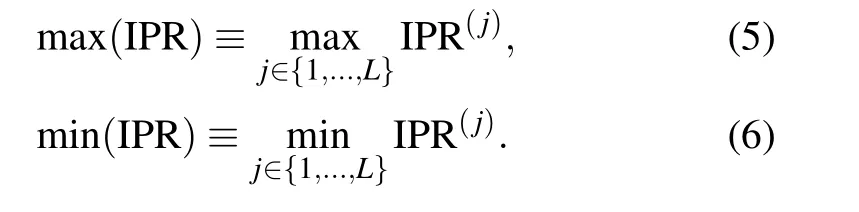
When max(IPR)diverges from zero but min(IPR)remains at zero, localized states start to appear and the system switches from the extended to the mobility edge phase.When min(IPR)also deviates from zero, the last extended state vanishes and the system enters a phase in which all states are localized. The maximal and minimal values of IPR can thus be used to distinguish phases with different localization nature and locate the corresponding phase boundaries.

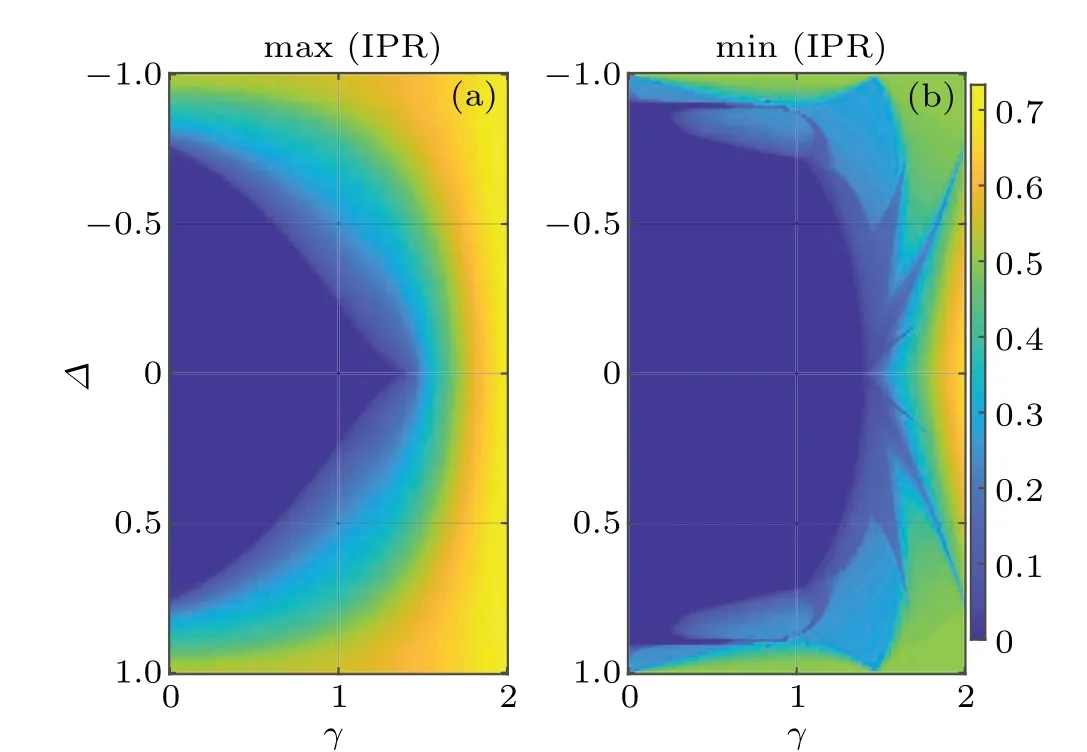
Fig.3. (a)The maximum and(b)minimum of IPRs versus the imaginary part of phase shift γ and hopping dimerization Δ. System parameters are set as J=1,V =0.5,and α =. The length of the lattice is L=610. PBC is taken in the diagonalization ?H.

To summarize, we find that the IPR can be viewed as an“order parameter”to describe the localization transitions in the dimerized NHQC. The behaviors of IPRs in distinct parameter domains could be employed to characterize the three different phases in the system. For completeness, we study the Lyapunov exponents of the system in Appendix B, and find consistent results as predicted by IPRs. We have also checked the spectrum and IPRs of the system under the open boundary condition (OBC), and find consistent results with those obtained under the PBC, excluding possible impact of non-Hermitian skin effects. In the following,we demonstrate that the localization transitions in our system are of topological origin,and can be depicted by a pair of spectral winding numbers.

3.3. Topological winding number

In previous studies,spectral winding numbers have been employed to characterize non-Hermitian topological matter in 1D clean and disordered systems.[52,73]For the dimerized NHQC, we can introduce a pair of winding numbers to describe the topological nature of its localization transitions.These numbers can be defined as

HeteNis the number of dimerized cells of the lattice and?=1,2. The phase shiftβ/Nis introduced into the Hamiltonian ?Hvia settingVn →Vcos(2παn+β/N+iγ). (?1,?2)are two real-valued base energies,and(w1,w2)count the number of times that the spectrum ofH(β/N)winds around these energies whenβsweeps over a cycle from zero to 2π. It is clear thatw1(w2) can be nonzero only if the spectrum of ?Haround?1(?2)takes complex values. These winding numbers are thus closely related to the complex spectrum structure of the system. When the spectrum does not possess a mobility edge,there is only a single base energy that can in principle be chosen arbitrarily,[52]and we would always havew1=w2. In our model this is the case whenΔ=0(uniform hopping). If mobility edges exist in the spectrum,the choice of base energies(?1,?2)should be related to its boundaries.[54]More precisely,in a given range of imaginary phase shift iγor hopping dimerizationΔ,we choose?1to be the real part of energy of the first eigenstate of ?Hwhose IPR starts to deviate from zero,i.e., the first eigenstate that becomes localized. Similarly, we set?2as the real part of energy of the last eigenstate whose profile changes from extended to localized.?1and?2thus decide the lower and upper bounds of the mobility edge on the ReE–γor ReE–Δplane. The winding numbersw1andw2defined with respect to?1and?2are expected to have quantized jumps when the mobility edge appears and vanishes in the spectrum.[54]

Fig. 4. The winding numbers (w1,w2) versus the imaginary part of phase shift γ. System parameters are set as J =1,V =0.5, Δ =0.4,α =. The size of the lattice is L=610 with PBC. The vertical dotted lines highlight the critical values γc1 and γc2, where transitions between different phases happen.

In Fig. 5, we present the topological phase diagrams of the dimerized NHQC versus the imaginary part of phase shift and hopping dimerization for two typical sets of system parameters. In the region ofρ ?0 [real spectrum, see also Fig.2(a)]and max(IPR)?0[all bulk states are extended,see also Fig. 3(a)], we findw1=w2=0, implying that thePTinvariant extended phase is topologically trivial according to the spectral winding numbers. Whenρa(bǔ)nd max(IPR) start to deviate from zero, the system undergoes aPT-breaking transition and enters a mobility edge phase. In the meantime,w1takes a quantized jump from 0 to?1, whereasw2remains at zero in Fig. 5(a). The transition from extended to mobility edge phases is thus topological and captured by the quantized change of winding numberw1. The mobility edge phase can also be viewed as a topological phase characterized by (w1,w2)=(?1,0). Whenρ ?1 and min(IPR) starts to deviate from zero,the system enters a localized phase and all bulk states take complex eigenvalues.Meanwhile,the winding numberw2jumps from 0 to?1 whereasw1remains at?1,as shown in Fig.5(a). Therefore,the transition from the mobility edge to localized phases is also topological and accompanied by the quantized change of winding numberw2by?1.The localized phase can then be viewed as a topological phase with(w1,w2)=(?1,?1). These observations are all demonstrated in the phase diagram Fig.5(a). We also considered other possible amplitudes of onsite potentialV[with one example given in Fig.5(b)],and obtain similar kinds of diagrams,which verifies the generality of our approach to the characterization of localization transitions and topological phases in dimerized NHQCs. We summarize the key results of this section in Table 1.

Fig. 5. Topological phase diagrams of the dimerized NHQC. System parameters are set as J=1,α =,and V =0.5(V =1)for panel(a)[panel(b)]. The length of the lattice is L=610,containing N=305 dimerized cells. In panels(a)and(b),each region with a uniform color corresponds to a topological phase, whose winding numbers are denoted therein. The extended, mobility edge and localized phases have(w1,w2)=(0,0),(?1,0)and(?1,?1). w1 or w2 jumps at a boundary between different phases. PBC is taken in the calculation.

Table 1. Summary of the results for the dimerized NHQC.

4. Discussion

In experiments, the dimerized NHQC might be engineered in photonic systems. The uniform part of hopping amplitude and non-Hermitian quasiperiodic potential could be realized by a frequency-modulated mode-locked laser with gain medium, phase modulator and low-finesse intracavity etalon,as proposed in Ref. [52]. The dimerized hopping amplitude could be realized by engineering the profile of refractive index in the model-locked laser setup.[76]Therefore,our model should be within reach in current or near-term experimental situations. To promote the detection and characterization of different phases in the dimerized NHQC, we also investigate its wavepacket dynamics in Appendix C,and find connections between the dynamical signatures and localization properties of the system.

In conclusion, we find localization and topological transitions in a dimerized NHQC, which are originated from the cooperation between hopping dimerizations and complex onsite quasiperiodic potential.In the region of weak dimerization and non-Hermiticity, the system is in an extended phase with real spectrum and delocalized eigenstates. With the increase of hopping dimerization and complex potential, the system transforms into a mobility edge phase. When the strength of hopping dimerization and non-Hermitian modulation become stronger,the system enters a third phase in which the spectrum is complex and all eigenstates are localized. Moreover, the transitions between the extended,mobility edge and localized phases are of topological nature. They can be characterized by the quantized jumps of two spectral winding numbers. Our results thus uncover the unique spectrum,topological and transport features of quasicrystals due to the interplay between hopping dimerizations and non-Hermitian onsite potential. The different phases and transitions found in our system further reveal the richness of localization and topological phenomena in non-Hermitian quasicrystals. In future work, it would be interesting to consider the impact of hopping dimerizations in other types of nonreciprocal and non-Hermitian quasicrystals,and explore the effect of nonlinearity,many-body interactions and skin effects on the localization and topological physics in dimerized non-Hermitian systems.

Appendix A:Details of the spectrum

In this appendix,we provide more details about the spectrum of the dimerized NHQC.In Fig.A1,we present the spectrum for a typical set of system parameters. When the imaginary part of phase shiftγis small, we observe real spectrum in Figs. A1(a) and A1(d), implying that the system is in thePT-invariant region.

Fig. A1. The spectrum of the dimerized NHQC model under PBC on the complex plane. System parameters are set as J =1, V =0.5,α =,and Δ =0.2(Δ =0.4)for panels(a)–(c)[(d)–(f)]. The values of the imaginary part of phase shift are shown in the panel captions.The length of the lattice is L=2584.

With the increase ofγ, the spectrum starts to become complex and develop loops on the complexEplane, which means that the system has undergone aPT-transition and roamed into aPT-broken region. However,parts of the spectrum are still pinned to the real axis in Figs.A1(b)and A1(e),indicating that the eigenstates with real and complex eigenvalues coexist in these cases. Whenγfurther increases, the number of eigenstates with real eigenvalues tends to decrease,and finally almost all states have complex energies,as shown in Figs.A1(c)and A1(f). Besides,the range and shape of the spectrum also depend on the dimerization strengthΔ, which reveals that both the hopping dimerization and complex onsite potential could affect the properties of the spectrum.

Appendix B:Lypunov exponent

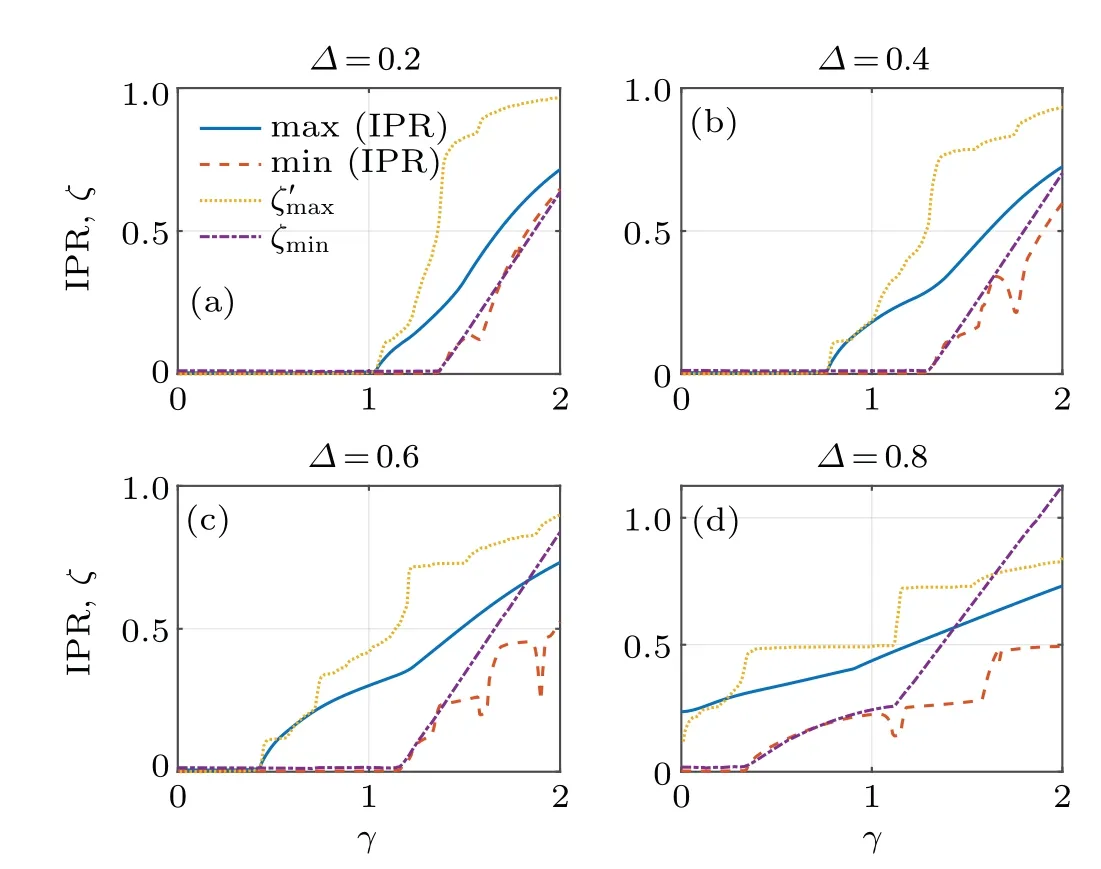
Fig.B1. IPRs and LEs versus the imaginary part of phase shift γ. System parameters are J =1,V =0.5, and α = The length of the lattice is L=610, and PBC (OBC) is taken in the calculation of IPRs(LEs). In panels (a)–(d), the solid (dashed) lines represent the maximum (minimum) of IPRs and the dotted (dash-dotted) lines show the derivative of the averaged(minimum of)LE.

Fig. B2. The minimum and derivative of LEs, as defined in Eqs.(B2)and(B3),versus the imaginary part of phase shift γ and hopping dimerization Δ. System parameters are set as J=1,V =0.5,and α=The length of the lattice is L=610 and the OBC is taken in the diagonalization ?H.

Appendix C:Wavepacket dynamics

In this appendix, we investigate the dynamical properties of the dimerized NHQC, and suggest to characterize the different phases by the spreading velocity and return probability of wavepackets. The evolution of a state in our sys-

In Fig.C1, we show the profiles of a wavepacket during the evolution and the averaged spreading velocity for a typical set of system parameters. In Fig. C1(a), the system is set in the extended phase (see also Fig. 4). We observe that the wavepacket indeed performs a ballistic spreading and presents a light cone pattern. In Fig. C1(b), the system is set in the mobility edge phase(see also Fig.4). The wavepacket is initially found to undergo a slow spreading over a finite range of sites. At a later stage,the spreading tends to terminate and the wavepacket retains a finite width around its original site. The initial spreading process may be assisted by the remaining extended states of the mobility edge phase.But during the evolution,the wavepacket develops more overlap with the localized states, which finally help to shut off its transport in the lattice. In Fig.C1(c),the parameters of ?Hare set in the localized phase(see also Fig.4). As expected,the wavepacket could not spread and remains exponentially localized around its original location. The distinctive signatures of wavepacket spreading in these three phases could then provide us with a dynamical way of distinguishing them. In Fig. C1(d), the spreading velocity of a wavepacket is found to decrease with the increase ofγwhen the system is set in the extended phase. At largeγ, the system enters the localized phase and the velocity approaches zero. Whenγgoes across the boundary between the extended and mobility edge phases, the velocity shows a quick drop in a small range ofγ, implying the appearance of a dynamical transition between these two phases. Notably,the critical pointγc1of the transition is different for different hopping dimerizations, and the velocity could also show an anomalous growth with the increase ofγin the mobility edge phase [e.g., see the solid line in Fig. C1(d)]. These observations suggest that the interplay between hopping dimerizations and complex onsite potential could not only create new types of dynamical phases in non-Hermitian quasicrystals, but also cause non-Hermiticity enhanced transport observed previously in systems with nonreciprocal hopping.[55]

Fig.C1. Profiles [in panels (a)–(c)]and spreading velocities [in panel(d)] of wavepackets initially localized at the central site of the lattice.The imaginary phase shift is set as(a)γ=0.4,(b)γ=1 and(c)γ=1.6.System parameters are J=1,V =0.5, Δ =0.4 in panels(a)–(c). The length of the lattice is L=1000 with PBC.The spreading velocity v is obtained in panel(d)after averaging v(t)over a time span of t=250.

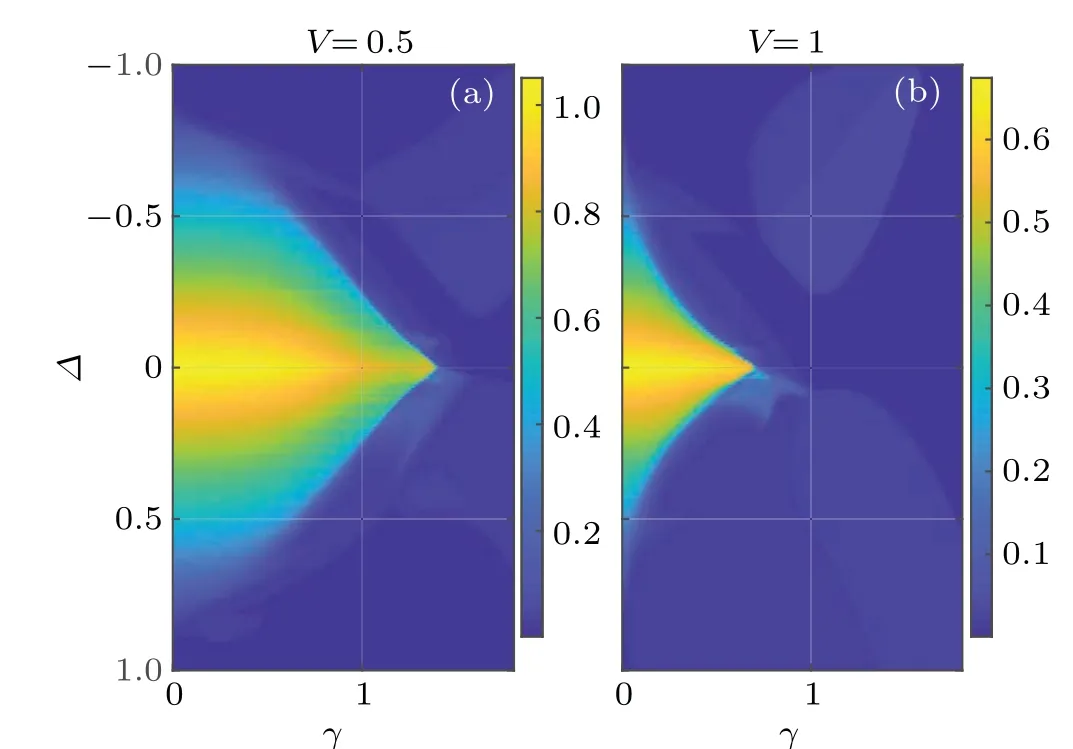
Fig.C2. Spreading velocities of an initially localized wavepacket versus the imaginary part of phase shift γ and hopping dimerization Δ.v(t)is averaged over a time duration t=250. The strength of the onsite potential is V =0.5 in panel(a)and V =1 in panel(b).System parameters are set as J =1 and α =. The length of the lattice is L=1000 with PBC,and the initial state satisfies〈n|ψ(0)〉=δn0.

In Fig. C3, we show the return probabilities of the initial states prepared in and quenched to different phases of the dimerized NHQC. In Fig. C3(a), the system is initialized in the extended phase with state profile|ψi|. When the postquench system is in the same phase,P(t) undergoes oscillations without a global decay, as shown by the blue solid line in Fig. C3(d). If the postquench Hamiltonian is in the mobility edge phase,P(t) first subjects to oscillations with a global decay profile,and approaches zero in the long-time domain, as demonstrated by the red dashed line in Fig. C3(d).The initial oscillations ofP(t)can be traced back to the presence of extended states in the mobility edge phase. With the progress of time, the state is trapped by localized states in the mobility edge phase, leading to the decay ofP(t)at larget. If ?Hfis in the localized phase,P(t) decays very fast and quickly approaches zero,as depicted by the yellow dotted line in Fig.C3(d). Since all states are localized in the postquench system, the evolving state can never go back. The distinctive features ofP(t)in three phases can thus help us to discriminate them following the postquench dynamics if the initial state is prepared in the extended phase.

In Figs. C3(b) and C3(c), we prepare the system into a localized state in the mobility edge and insulator phases. The results in Figs. C3(e) and C3(f) suggest that the return probabilities also behave distinctly when ?Hfis set in phases with different transport nature. Putting together, we conclude that wherever the initial state is prepared,its return probability following quenches to different phases could help us to distinguish them dynamically. In experiments,the averaged spreading velocity and return probability of the wavepackets can thus be employed to detect phases with different localization nature in the dimerized NHQC.

Fig. C3. Profiles of the initial states [in panels (a)–(c)] and their return probabilities following quenches [in panels (d)–(f)] in the dimerized NHQC.The states in panels(a)–(c)are chosen to be the ones with the largest imaginary parts of energy at the corresponding phase shift γi.System parameters for panels(a)–(c)are set as J=1,V =0.5,Δ =0.4,α =,and the length of the lattice is L=610 with PBC.In panels(d)–(f),the curves correspond to return probabilities of the initial states in panels(a)–(c)following quenches of γ from the corresponding γi to different values of γf applied at t=0.