Strange quark star and the parameter space of the quasi-particle model

Wen-Hua Cai and Qing-Wu Wang

College of physics, Sichuan University, Chengdu 610064, China

Abstract The properties of strange quark stars are studied within the quasi-particle model.Taking into account chemical equilibrium and charge neutrality, the equation of state (EOS) of(2 +1) -flavor quark matter is obtained.We illustrate the parameter spaces with constraints from two aspects: one is based on the astronomical results of PSRJ0740+ 6620 and GW 170 817 ,and the other is based on the constraints proposed from the theoretical study of a compact star that the EOS must ensure the tidal deformability L1 .4 =and support a maximum mass above1.97 ⊙M.It is found that neither type of constraints can restrict the parameter space of the quasi-particle model in a reliable region and thus we conclude that the low mass compact star cannot be a strange quark star.

Keywords: strange quark, compact star, tidal deformability, quasi-particle model, neutron star

1.Introduction

Quantum chromodynamics(QCD),which has been regarded as the theory to govern the strong interaction, predicts that confined hadronic matter will undergo a deconfinement transition to a new phase at large density and extremely low temperature[1,2].It is believed that the new phase of nuclear matter,as we call it quark–gluon plasma(QGP),may exist within a new kind of compact star – quark stars [3–8].The strange quark matter(SQM) hypothesis indicates that the matter formed by a deconfined u quark, d quark and s quark may be the true ground state of strongly interacting matter [9, 10].This hypothesis supports the presence of a strange quark star.

In recent years,based on the latest astronomical data,some researchers have argued that many compact stars and pulsars with large mass may be strange quark stars, even including some stars which used to be identified as neutron stars [11].This naturally raises the question of how to discriminate these strange quark stars from other compact stars.At present,due to the lack of astronomical observation data, it may be achieved through analysis of properties,like the mass–radius relation and tidal deformability, which heavily depends on studying the equation of state (EOS)[12, 13].Applying an EOS to the Tolman–Oppenheimer–Volkoff (TOV) equation, the relevant properties and features of the star can be obtained.However,at high density and very low temperature, it is difficult to figure out the EOS of cold deconfined quark matter from first principles.Hence, people study the properties of QGP and strange quark stars based on nonperturbative models like the MIT bag model[14–17],the Nambu?Jona-Lasinio(NJL)model[18–22]and the quasi-particle model [22–24].

The quasi-particle model is a kind of phenomenological description of QGP which was obtained by the simulation of lattice QCD [25].Via the introduction of thermal mass at finite temperature and finite chemical potential, we can treat the system as made up of free quark gas to avoid the complicated calculation of QCD interactions.Thanks to the increasing data from astrophysical observations, it provides a place to test the applicability of an effective model.The latest astrophysical observation of a pulsar, PSRJ0740+ 6620[26], has provided a maximum mass measurement result so far, which is much larger than the result of PSRJ0348 +0432(M= 2.01 ±0.04M⊙)[27],and thus the soft EOSs which cannot produce such a massive star are supposed to be eliminated.Moreover,according to the gravitational wave observation GW 170 817 [28], the tidal deformability L for 1.4 M⊙star( L1.4) needs to be constricted to smaller than 800 in the low-spin prior case.Recently,some significant conclusions have been drawn via the study of quark matter within compact stars, taking into account both the astronomical observations and theoretical simulations [29].Adopting the speed-of-sound interpolation method, they have succeeded in describing the QCD matter properties of different compact stars with different masses and radii.Their results have been verified by approximately 570 000 EoSs which are built from randomly generated functions.To get such a result, some hypothetical constraints are proposed that the maximum mass should be above 1.97 M⊙a(bǔ)nd the range of tidal deformability should be revised to L1.4=190Recently, some scholars have even claimed that there may exist a compact star with a mass of 2.6 M⊙[30,31],which presents great potential to be a candidate for a strange quark star if it is proven to be true.In this paper, from the perspective of strange quark stars, we intend to study the parameter space of the quasi-particle model with some of the latest astrophysical results.

This paper is organized as follows.We first introduce the quasi-particle model at finite chemical potential based on statistical mechanics and thermodynamic equilibrium in section 2.By considering chemical equilibrium and charge neutrality, the EOS of SQM is obtained in section 3.Then,making use of the the EOS, the mass–radius and tidal deformability of a strange quark star are explored.Based on the latest astronomical observations and theoretical research,we study the parameter space of the quasi-particle model.Finally, a short summary of our work is given in section 4.

2.Quasi-particle model at finite chemical potential and zero temperature

The quasi-particle model,which was first proposed to explain the results in lattice gauge theory (LGT) simulations, is widely used to describe the nonperturbative behavior of QCD.Following the works of Bannur[32–36],the density of quarks at nonzero temperature is given by

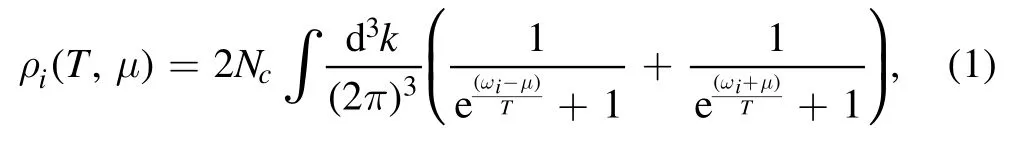
where Ncis the number of colors and subscript i indicates the u, d and s quarks.In addition,

is the dispersion relation for each kind of quark, wherem i(T,μ)stands for the effective mass of different quarks and has the expression

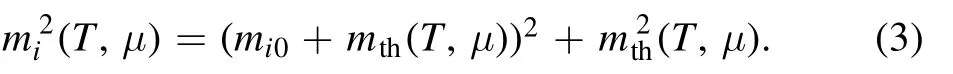
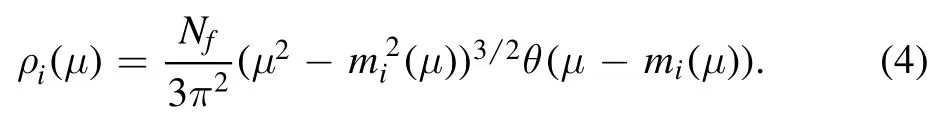
The symbol θ in equation (4) stands for the step function.In this case, the thermal massmthin equation (3) reads

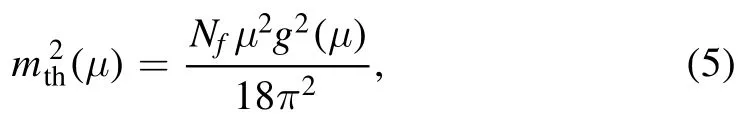
in which the symbol Nfis the number of flavors.The effective coupling constant g can be obtained by the two-loop approximation and has the form

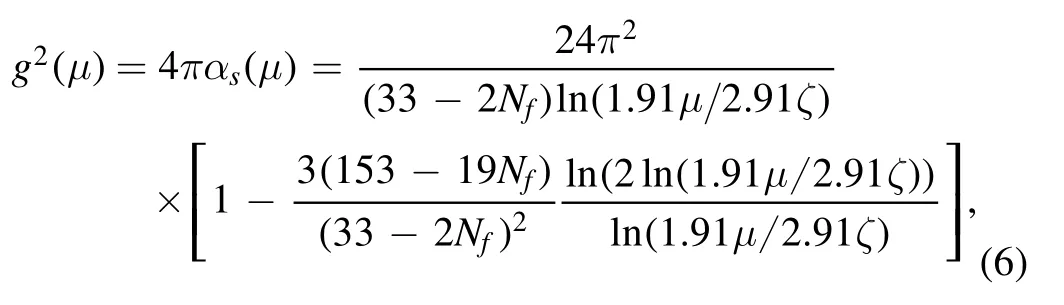
where ζ is a phenomenological parameter which is related to the nonperturbative effect of QCD [38, 39].Making use of the physical quantities introduced above, all the physical quantities needed to describe the SQM can be derived through the basic thermodynamic relations.

The relation between number density of quarksρi(μ)and chemical potential μ is presented in figure 1.Owing to the step function in the expression ofρi(μ), it is found that the quark number density vanishes when the chemical potential is below a critical pointμc.That is to say,μ=μ cis a singularity which divides the quark number density into two different regions.This phenomenon is in agreement with the conclusion brought forth in [40], in which researchers pointed out that the existence of some singularity at critical point with zero temperature is a robust and model-independent result based on a universal argument.Similar discussions may also be found in [41, 42].

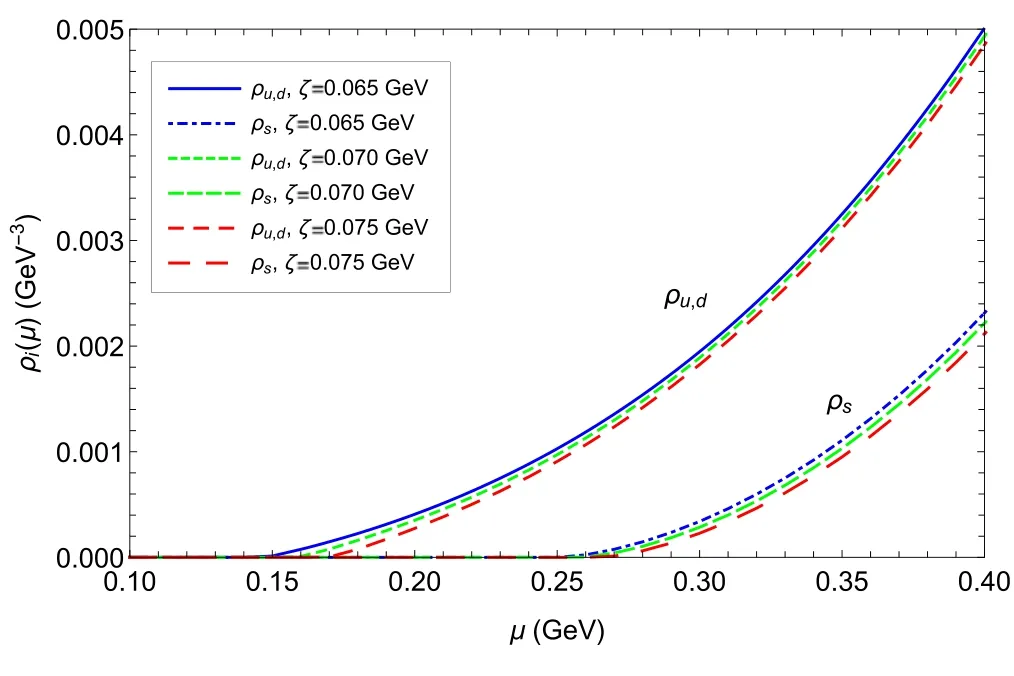
Figure 1.Number density ρi ( μ)of u, d and s quarks as functions of chemical potential μ at zero temperature with ζ = 0.065 GeV,0.070 GeV and 0.075 GeV respectively.

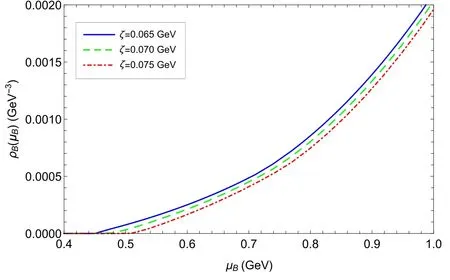
Figure 2.Baryon number densityρB as a function of baryon chemical potentialμB with ζ = 0.065 GeV, 0.070 GeV and 0.075 GeV, respectively.

3.Structure of strange quark stars with the quasiparticle model

Recently, research on strange quark stars has attracted increasing attention.The existing theories suggest that strange quark stars have at least two main channels to be produced.First, a number of them may come into being in the early stage of the universe according to the Big Bang theory.Second, they can also be produced by the phase transition within neutron stars [11].Therefore, studying strange quark stars does help to understand the phase transition from confined hadron matter to quark matter.

To begin with,there exists chemical equilibrium with the compact stars which is established via weak decay

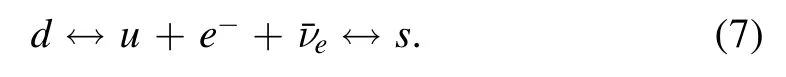
In consideration of the equilibrium, the electrons and neutrinos have to be included in the system.However,for a stable quark star, we can reasonably assume the neutrinos have enough time to leave the system,which means that there is no need to consider the participation of neutrinos in the chemical equilibrium.To that end, the constraint conditions

and

for the chemical potential of u,d,s quarks and electrons have to be met.Moreover, taking electric charge neutrality into account, the number densities of quarks and electrons should be bound to satisfy the relation

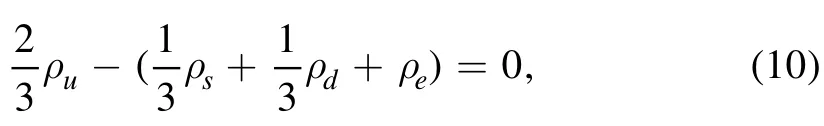
The EOS of quark matter at zero temperature can be derived from statistical mechanics and reads [43, 44]

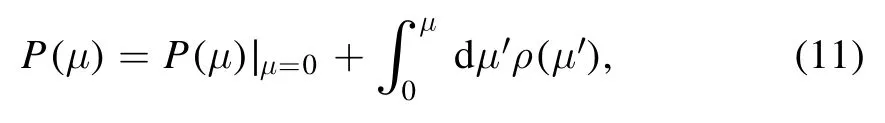
whereP(μ)∣μ=0is a negative term.The termP(μ)∣μ=0is the so-called vacuum pressure which is related to the confinement property of QCD.However,due to the lack of comprehensive understanding of QCD interactions,we can neither obtain this term from first principles nor figure out how it is generated.Therefore, we treat the vacuum pressure term as a phenomenological parameter and rewrite it asP(μ)∣μ=0= -B(B＞0) in this paper.Then, the energy density can be deduced from the thermodynamic relation

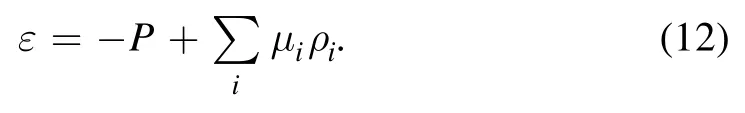
Combining equation (11) and equation (12) with the discussion taken before, some significant relations can be obtained.

The influence of parameter ζ, parameter B and baryon chemical potentialμBon the EOS of SQM is presented in figures 4 and 5.We can see that the pressure densityP(μB)and the energy densityε(μB)have similar behaviors: whenμB＜μBc,P(μB)andε(μB)remain constant, and the reason for this phenomenon is the disappearance of the quark number density in this region; onceμB＞μBc, they becomemonotonically increasing functions of baryon chemical potentialμB.We exhibit the relation between the pressure density and energy density in figure 6.It can be found that the EOS with a larger ζ and a larger B becomes softer.In addition,there is a starting point of the EOS,(-B,B)in the plane of energy–pressure density, which is the consequence of equation (11).

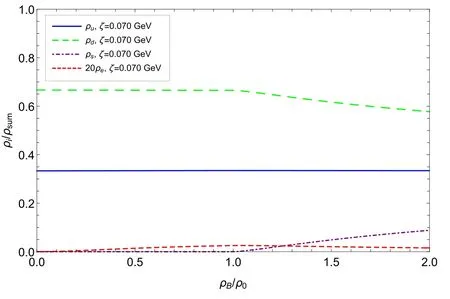
Figure 3.Proportion of constituent u, d and s quarks and electrons(multiplied by a factor of 20) as functions of the baryon number density (the symbolρsum stands for the total quark number density andρ0 stands for the baryon number density where the s quarks begin to be nonzero).

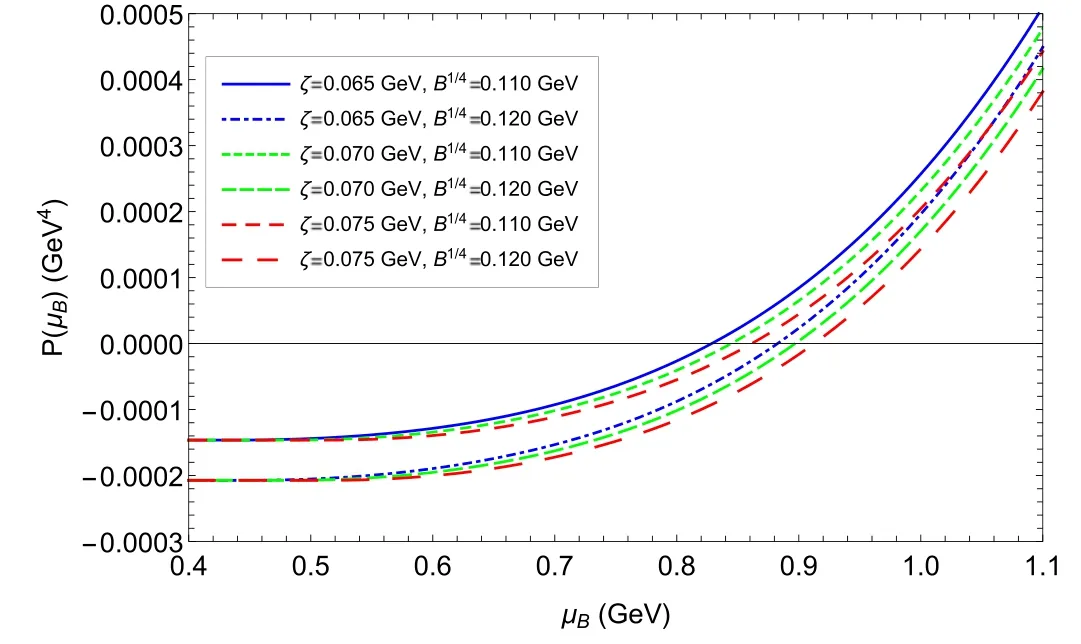
Figure 4.Pressure density P( μB)as a function of baryon number densityμB for different ζ and B.

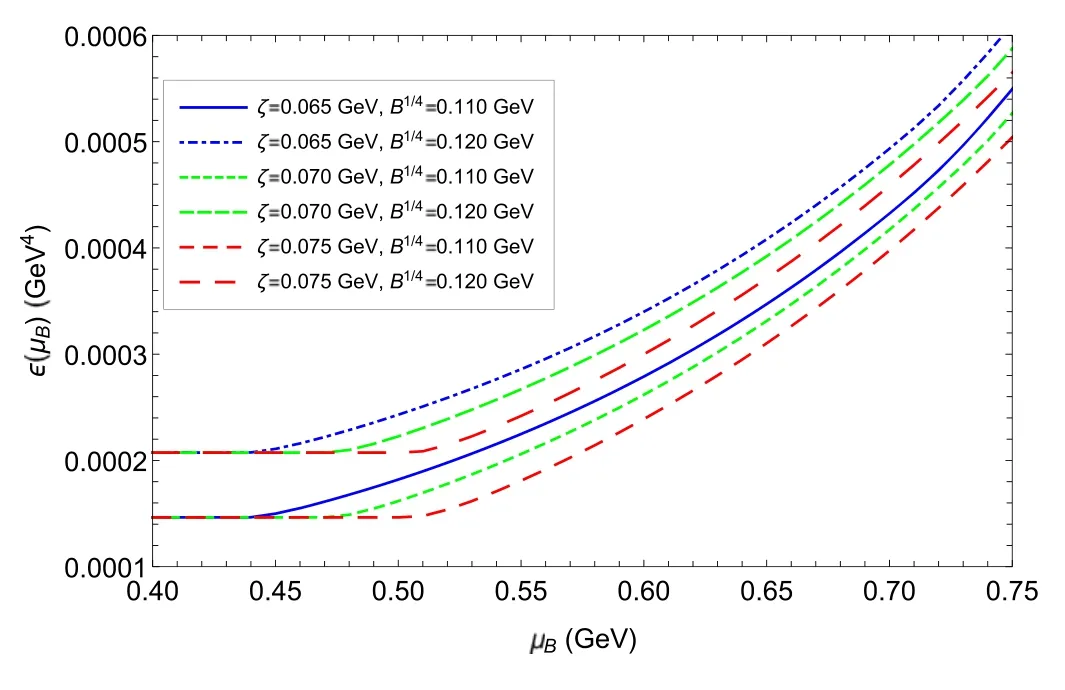
Figure 5.Energy density ε ( μB)as a function of baryon number densityμB for different ζ and B.

Utilizing the EOS of SQM, we can get the mass–radius relations (in units ofG=c= 1) by integrating the TOV equations [45–47]

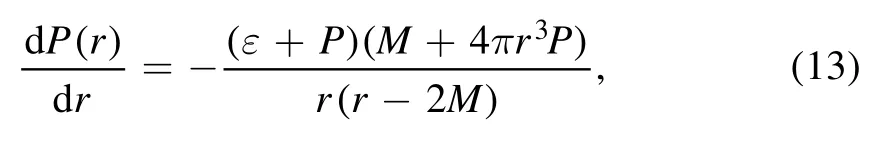
and

and the result is exhibited in figure 7.As a comparison, we also show the maximum mass constraints required by PSR J0740 +6620(M=and PSRJ0348 +0432(M= 2.01 ±0.04M⊙),as well as the restriction proposed in[29] in this figure.It is easy to find in figure 7 that a larger maximum mass will be generated with a stiffer EOS.Furthermore, we can find that the EOSs of quasi-particles have the ability to yield a maximum mass larger than the latest observation results.The maximum masses and the corresponding radii of strange quark stars with different ζ and B are calculated, and the results are exhibited in table 1.From this table we can see clearly that the radius of the strange quark star with a mass of near 2 M⊙is close to 12 km.The results are in agreement with the discussions in [48–51].

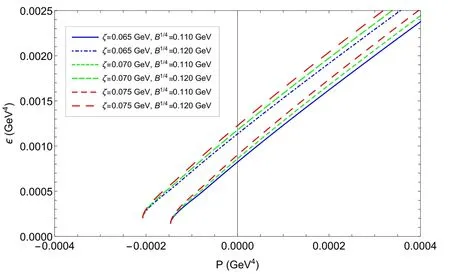
Figure 6.Relations between energy density ε and pressure density P for different ζ and B.

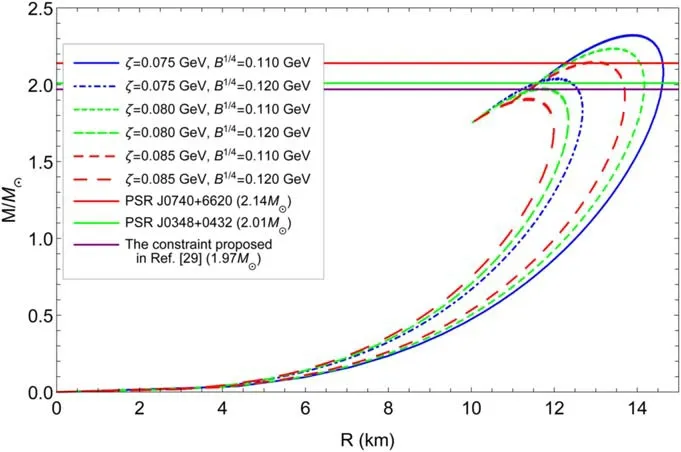
Figure 7.Mass–radius relations of strange quark stars for different ζ and B with the constraints required by PSRJ0740+ 6620,PSRJ0348+ 0432.

In a binary star system,each star will be deformed by the tidal field of its companion because of the presence of tidal gravity.This phenomenon can be described by the physical quantity ‘tidal deformability,’ which is defined as the ratio between one star’s induced mass quadrupole moment and the tidal field of its companion [47].

In order to calculate the tidal deformability L, we adopt the relation

whereC=represents the compactness of a star.Here,the physical quantity k2is the dimensionless tidal Love number for l = 2 which describes the difficulty with which a star can be deformed by an external tidal field, and it can beexpressed as

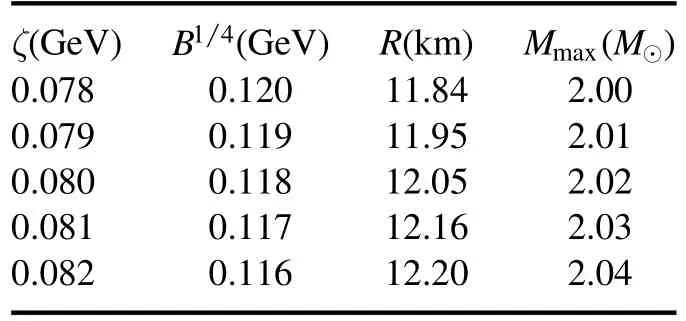
Table 1.Radii R and maximum masses Mmax of strange quark stars with different ζ and B.

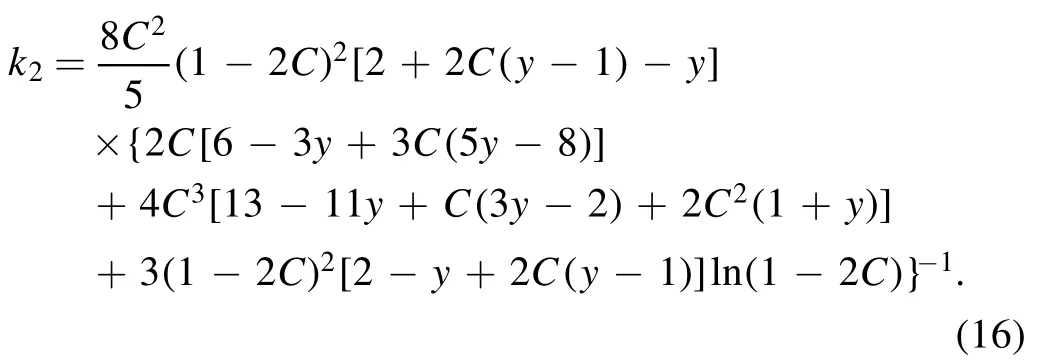
In equation (16), the symbol y is defined as

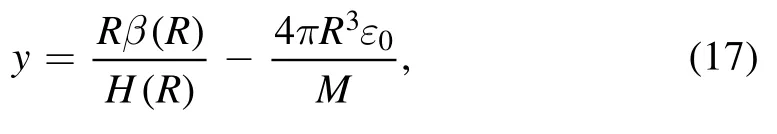
and is related to metric functionH(r) and surface energy densityε0.Due to the introduction of negative vacuum pressure, there is a nonzero energy density just around the surface of the star as we can see in figure 6.To derive the metric function, it is necessary to integrate the following differential equations:

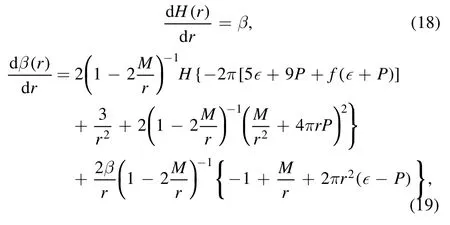
where

The integration will start from the center with the expansionsH(r) =a0r2andβ(r)=2a0ras the radiusr→0.Since our concern is the ratio ofwe can ignore the value of coefficient a0and treat it as 1 for simplicity.

Combining the discussions above, the properties of strange quark stars with 1.4 M⊙for different ζ and B can be obtained, as presented in table 2.From this table we can see that the strange quark star is less compact with a smaller ζ and a smaller B for a given mass.This result means that such a star is easier to be deformed by an external tidal field.We illustrate in figure 8 the relations between the tidal deformability for a 1.4 M⊙strange quark star( L1.4)and parameters ζ as well as the relations between L1.4and parameter B.For comparison, we also show the constraint required by GW 170 817 that the L1.4should be smaller than 800 in the same figure.We can find in figure 8 that not all the parameter settings satisfy the constraint from gravitational wave observations.

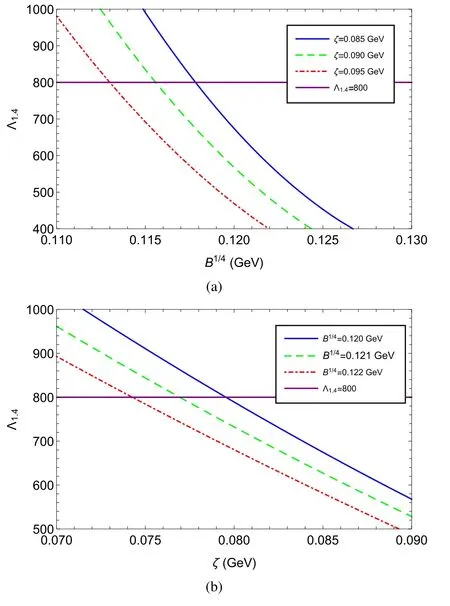
Figure 8.Tidal deformability as function of parameter ζ and bag constant B.(a)Relations betweenL1.4 and parameter ζ;(b)relations betweenL1.4 and parameter B.

Table 2.Properties of strange quark stars with a mass of 1.4 M⊙for different ζ and B, including the compactness C =the Love number k2 as well as the tidal deformabilityL1.4.

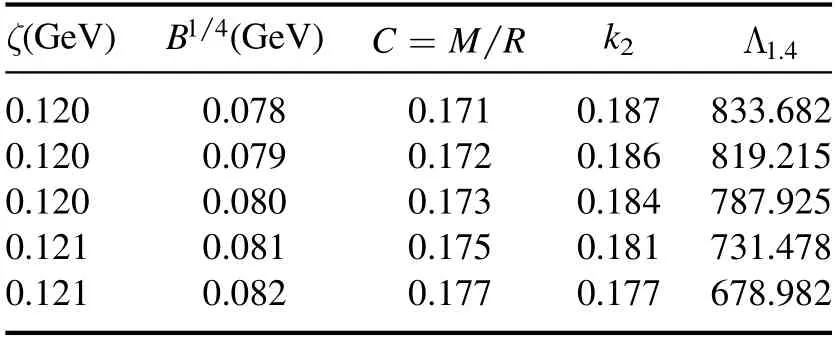
Table 2.Properties of strange quark stars with a mass of 1.4 M⊙for different ζ and B, including the compactness C =the Love number k2 as well as the tidal deformabilityL1.4.

ζ(GeV)B14(GeV)=C M R k2 L1.4 0.120 0.078 0.171 0.187 833.682 0.120 0.079 0.172 0.186 819.215 0.120 0.080 0.173 0.184 787.925 0.121 0.081 0.175 0.181 731.478 0.121 0.082 0.177 0.177 678.982

In figure 9,we illustrate the parameter space of the quasiparticle model based on the astronomical observations and theoretical results respectively.In panel (a), we constrain the parameters in view of the PSR J0740+ 6620and GW 170 817 , and find that there is no coincident region for the feasible area of PSR J0740 +6620 and the feasible area of GW 170 817.Namely,the constraint of GW 170 817 , which requires L1.4to be smaller than 800 , and the constraint of PSRJ0740 +6620which requires a maximum mass above 2.14 M⊙, cannot be met simultaneously.Considering the uncertainty of the mass,it can fit to the low boundary of mass asζ≤0.06 GeV.Similarly,we draw another parameter space in panel (b), which is based on the requirement proposed in[29].In [29], researchers claimed that the EOS must ensure the tidal deformabilityand support a maximum mass above 1.97 M⊙.It is clear to see from(b)that the two feasible areas do not coincide when ζ is larger than about 0.03 GeV,and in the region ofζ＜0.03 GeV,there is a small coincident area for the two constraints, which almost vanishes.However, according to [52], the quasi-particle model we use will work better in the large ζ region in order to fit the LGT data; as for the area of small ζ, the results may be unreliable to some extent, let alone the coincident region which is very small compared to the whole parameter space.

In figure 9 the parameter space of the quasi-particle model cannot meet the the constraints of PSRJ0740+ 6620and GW 170 817 simultaneously.Meanwhile, the parameter space also cannot restrict the requirement proposed in[29]in a reliable region.Up to now,increasing evidence has indicated that the compact stars of large masses may be strange quark stars[53–56].On the basis of the results in figure 9, we think it is probably improper to regard a compact star with a mass of 1.4 M⊙a(bǔ)s strange quark star.Naturally,we assume that the properties of compact stars with small mass (including 1.4 M⊙) look more like neutron stars formed by hadronic matter rather than strange quark stars.This hypothesis is consistent with the conclusion of[29], in which the researchers claimed that they found quark matter exists within compact stars with 2 M⊙but is not present within compact stars with1.4⊙M.

Figure 9.Parameter space of the quasi-particle model based on observation results of PSRJ0740 +6620 and GW 170 817 and based on constraints proposed in[29],respectively.

4.Summary

In this paper,we have studied the properties of strange quark stars with the quasi-particle model.Taking the chemical equilibrium of the weak interaction and charge neutrality into account,we have obtained the baryon number density and the variation of constituents for different ζ.We have found that the proportions of quarks are irrelevant with ζ.With the introduction of parameter B for the vacuum pressure,we have established the EOS of SQM.With proper choices of B and ζ,it is possible to generate a quark star with a maximum mass larger than2.14⊙M, which matches the results of PSR J0740 +6620and PSRJ0348 +0432(M= 2.01 ±0.04M⊙).We have calculated the properties of a strange quark star with mass of1.4⊙M, including the compactness C, the Love number k2and the tidal deformability L1.4.It is found that a softer EOS corresponds to a more compact quark star, which is more difficult to be deformed.

Finally, we have illustrated the parameter space of the quasi-particle model based on astronomical observations and theoretical suggestions.It is found that the parameter space cannot meet the constraint of GW 170 817 which requires L1.4smaller than 800 , and the constraint of PSRJ0740+ 6620which requires a maximum mass of at least2.14⊙M, simultaneously.Similarly, the model also cannot satisfy the constraints proposed in [29], in which the researchers claimed that the EOS must ensure the tidal deformabilityand support a maximum mas s above1.97⊙M.

Early studies on neutron star models are in good agreement with the observed data of low mass stars.However, the EOSs are relatively soft, so it is difficult to get a maximum mass larger than 2⊙M.We can obtain large mass objects based on the EOS of SQM, but cannot obtain correct Λ data for stars with small mass simultaneously.Therefore, in order to meet the Λ data from the present astronomical observations, it is not feasible for the present three flavored quark model.Of course, our conclusion should be understood as model dependent.There may be other possibilities, such as thinking of a pulsar as a three flavored gigantic nucleus which is called a strangeon star [57].In figure 1 of [57], with L( 1.4)=400, the maximum mass of strangeon stars can be larger than3⊙M.Therefore,our calculations as compared with the quark-cluster model of a strangeon star may indicate that the coupling between quarks in a strange star is still very strong so that quarks are localized/confined in strangeons,as is in the case of nucleons for a nucleus.A recent work assuming the SQM is in the color–flavor locked phase has found that the color superconductivity gap is poorly constrained by those observed global properties of a1.4⊙Mstar[58].As such, it is suggested to use a hadronic EOS in exploring the properties of low mass compact stars while using a pure quark EOS or hybrid EOS in studying compact stars with larger mass.

Acknowledgments

This work is supported by the Cultivating Plan of Characteristic Direction of Science (2020SCUNL209).