Analysis of the wave functions for accelerating Kerr-Newman metric
Yi-Gu Chen, Hai-Bo Wei, Hui Zheng, Zai-Dong Wangand Zhong-Heng Li
College of Science, Zhejiang University of Technology, Hangzhou 310023, China
Abstract As is well-known,it is very difficult to solve wave equations in curved space-time.In this paper,we find that wave equations describing massless fields of the spins s≤ 2 in accelerating Kerr-Newman black holes can be written as a compact master equation.The master equation can be separated to radial and angular equations, and both can be transformed to Heun’s equation,which shows that there are analytic solutions for all the wave equations of massless spin fields.The results not only demonstrate that it is possible to study the similarity between waves of gravitational and other massless spin fields, but also it can deal with other astrophysical applications, such as quasinormal modes, scattering, stability, etc.In addition, we also derive approximate solutions of the radial equation.
Keywords: massless spin fields, wave equation, Heun’s equation, accelerating Kerr-Newman metric
1.Introduction
Perturbation theory is a significant method to study properties of black holes.It was first introduced by Regge and Wheeler to study the stability of Schwarzschild black hole in 1957[1].Now the study of black hole perturbation involves the study of scattering[2],quasinormal modes[3],gravitational waves,etc.In 1962, Newman and Penrose [4] started from the null tetrad methods, and established a spinor technique, often called the NewmanPenrose (NP) formalism, which is a powerful tool for analyzing the black hole perturbation.In 1973, Teukolsky [5], employed the NP formalism, and succeeded in disentangling the perturbations of the Kerr metric,and wrote a master equation for the massless scalar (s = 0),Weyl neutrinoelectromagnetic (s=1), and gravitational (s=2) fields [2].In 1998, Suzuki et al [6] showed that a master equation for massless particles with arbitrary spins (s≤ 2) in Kerr-de Sitter space-times can be reduced to Heun’s equation.In 2015,Jiang et al[7]found that the master equation in Kerr-Newman-(anti) de Sitter geometries is also an Heun’s equation in disguise.In this paper, we extend the study to perturbations of accelerating Kerr-Newman black holes.
The paper is organized as follows: In section 2 we introduce some properties of the metric of accelerating Kerr-Newman black hole.In section 3 we obtain a compact master equation from general perturbation wave equations.In section 4, we separate the master equation and transform radial equation and angular equation to Heun’s equation.In section 5 we apply an approximation method to obtain wave function solutions in an event horizon.Finally, in section 6,we discuss and conclude.
2.The properties of metric
While the prehistory of accelerating black holes is quite long and convoluted, with original based contributions dating as far back as the C-metric of 1917 [8, 9], significant attention from within the gravitational community dates back to physical interpretation of Kinnersley and Walker [10] in 1970.They showed that the C-metric describes a pair of black holes undergoing uniform acceleration.In 2005,Hong and Teo[11]first proposed the accelerating Kerr-Newman metric,which in Boyer-Lindquist-like coordinates reads [12]:
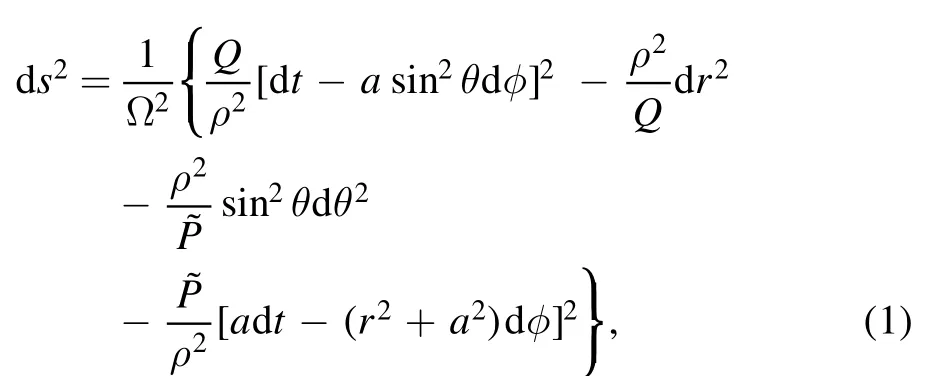
where the functions Ω,ρ2,and Q are defined by
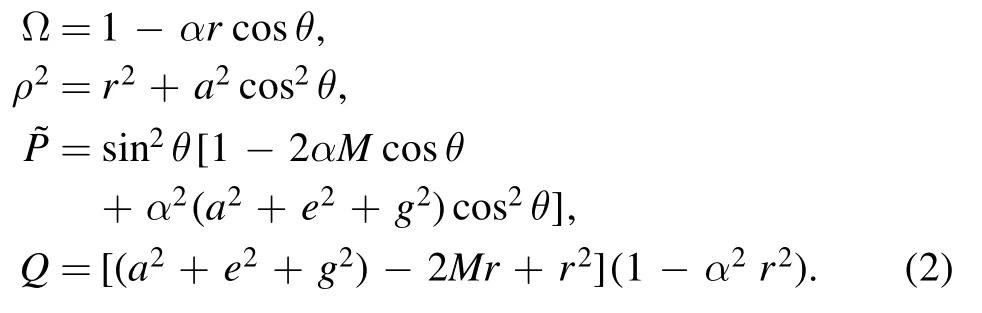
This metric is dependent on five arbitrary parameters,where M describes the mass of source, a describes the uniform rotation of black holes, e and g describe electric and magnetic charge.Parameter α is related to the acceleration of black holes.A pair of rotating charged black holes with uniform acceleration at opposite directions are represented by this metric [13].The expression of this metric includes the Kerr-Newman black hole whenα= 0 and the charged version of the C-metric when a = 0 [12, 14].
Here we introduce singularities of the accelerating Kerr-Newman metric.The ring singularity will occur whenρ2= 0,which is equivalent to r = 0 andcos2θ=0[14].The axial singularity generally occurs on the rotational axis as a conical singularity whensinθ=0, which is usual a true singularity,but it will be just a coordinate singularity when the parameterα= 0[14].The conical singularity on one half of axis can be removed by specifying the range of φ[15].Ω in the metric is the conformal factor and conformal infinity will occur when Ω is vanishing.The roots of= 0and Q = 0are both coordinates singularities.Points at which= 0generally correspond to poles of the coordinates and surface on which Q = 0 are killing horizons [16].
Four solutions of Q = 0 are
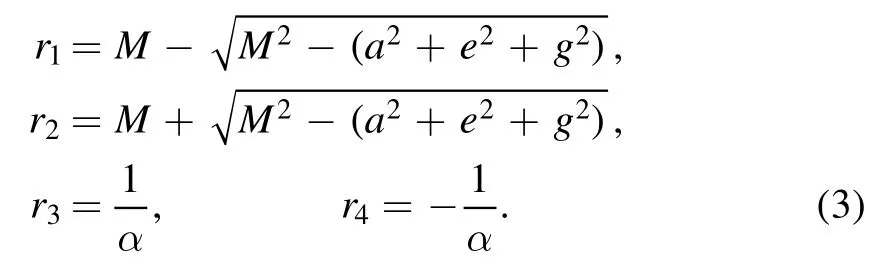

It is convenient to make a coordinate transformationη= cosθto describe the four solutions of= 0.They are:
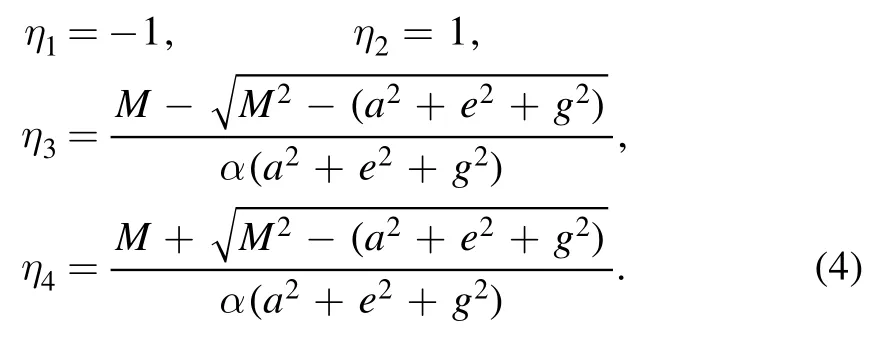
And we should ensure that the values ofη3andη4less than 1.
We introduce a null tetrad (l,n,mand):
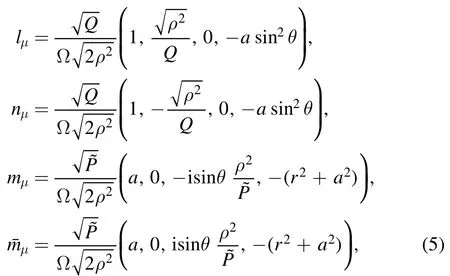
which satisfies orthonormal relations:lμ mμ=lμ==1.
We can obtain the spin coefficients by using metric (1)and tetrad (5) [2, 17]:
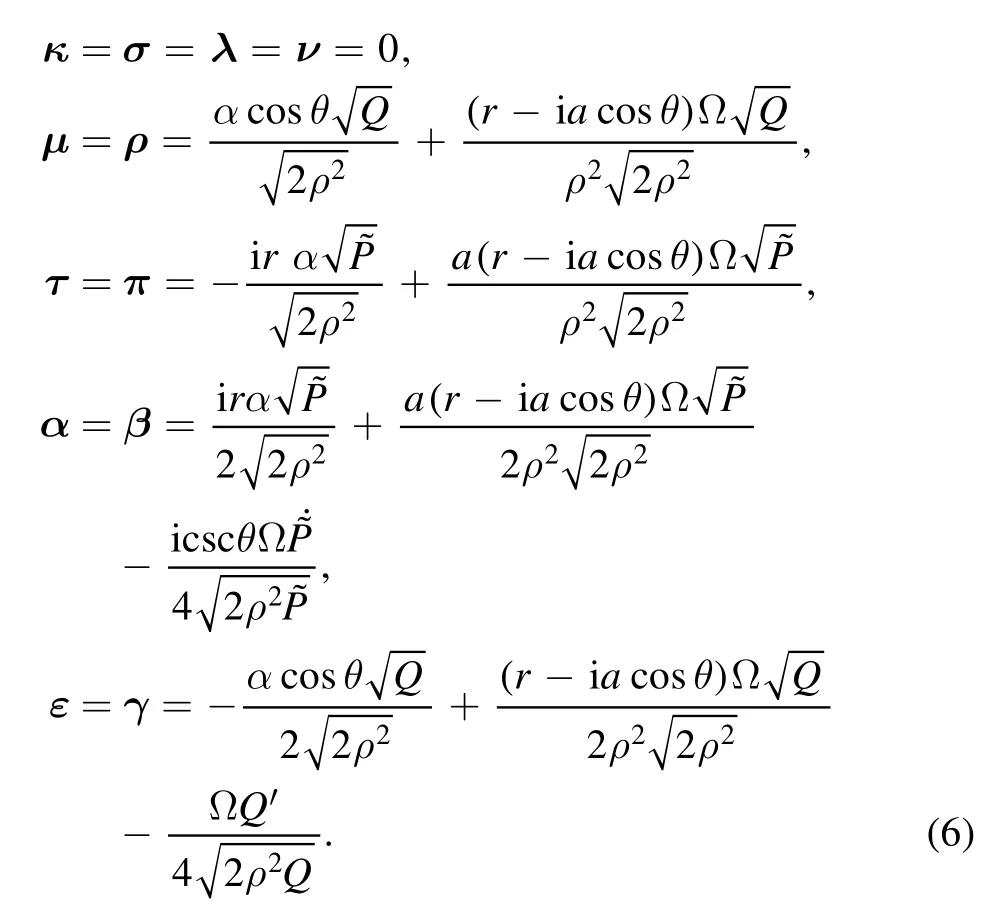
Here we use prime notation on the letter to denote the derivative with respect to r and the dot notation on the letter means of the derivative with respect to θ.The spin coefficients can describe some characteristics of space-times.The value ofκ=σ=λ=ν= 0 means that the null tetradlandnform a congruence of null geodesics and they are affine parameterization.According to the Goldberg-Sachs theorem,we know that the accelerating Kerr-Newman metric belongs to the Petrov type-D space-times [2].The minus(plus) value of real part ofρdescribes the expansion (or the contraction)of space-times, and the imaginary describes the rotations [2].
In terms of the tetrad (5), the only non-vanishing Weyl scalar is [13]:

3.Wave equations in Accelerating Kerr-Newman Background
In all type-D metrics,the massless field equations of spin 1/2,1, 3/2, 2 can be decoupled in the case of perturbations, and these equations for the source free case can be written into[17, 18]:
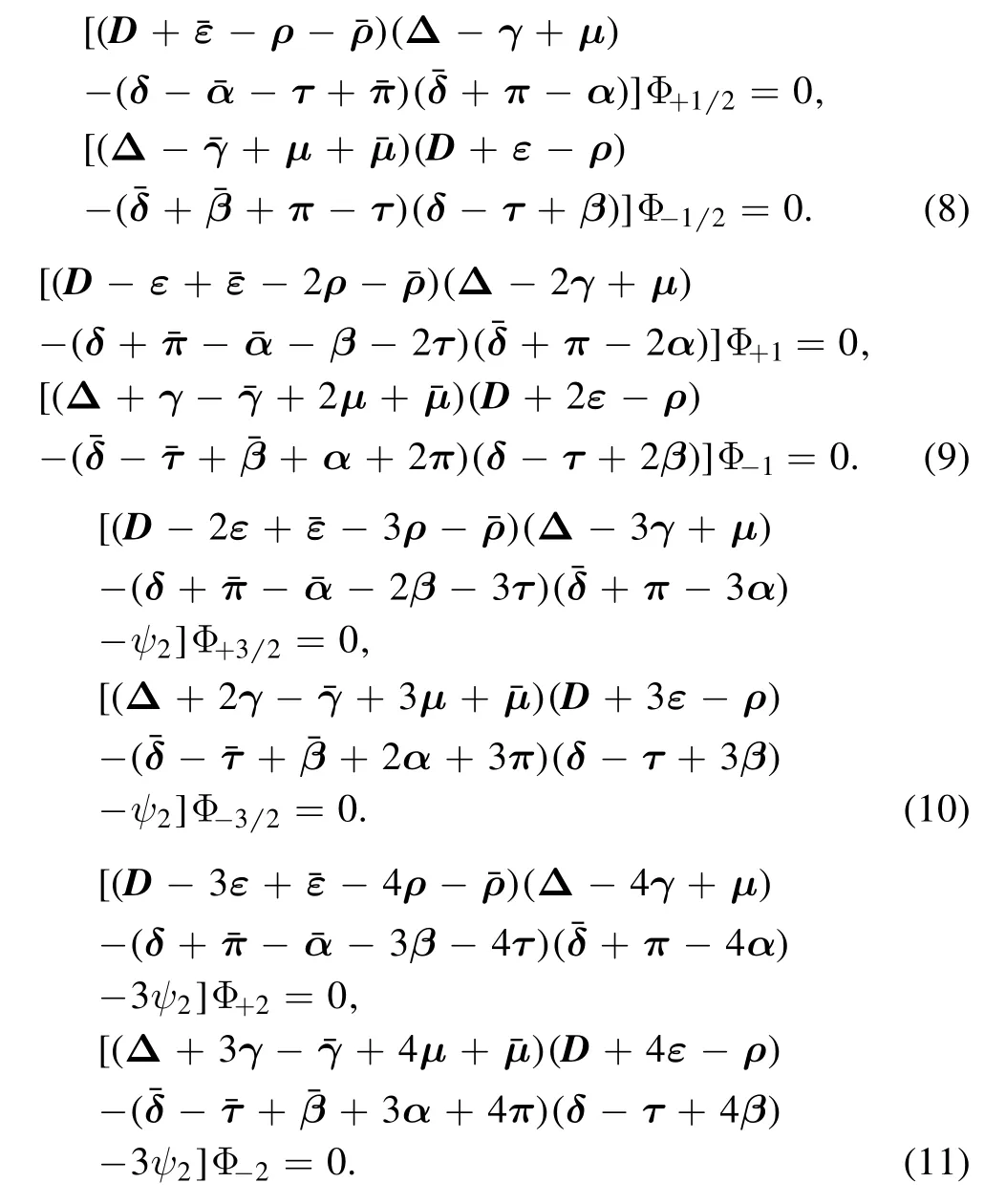
HereD,Δandδare the direction derivatives defined by:
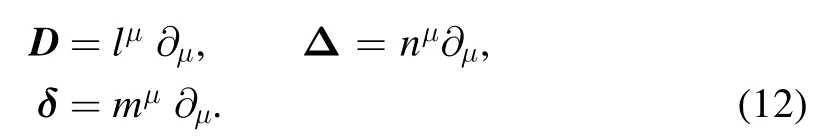
Introducing a new functionΨpvia the relation:
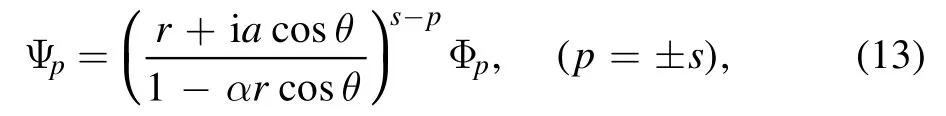
we find that equations(8)–(11)can be combined into a single statement:
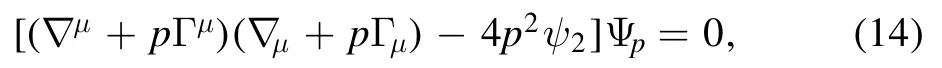
where ?μdenotes the covariant, the spin-coefficient connection [19]Γμhave the forms:
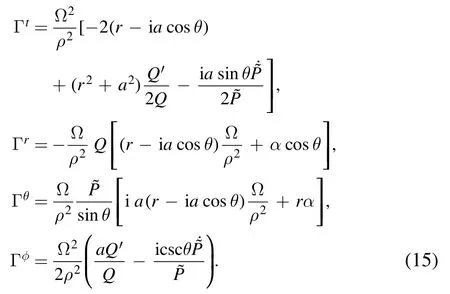
In this paper, the equation (14) is called the compact master equation.Evidently, when p = 0, equation (14) is just the massless scalar field equation.Therefore, equation (14) governs not only the massless fields of spin 1/2, 1, 3/2, and 2,but also the scalar field.Equation (14) tells us that the massless field equations for the spinss≤ 2 have such a similar structure in accelerating Kerr-Newman space-time.Therefore,any massless field of the spins< 2 can be used to simulate gravitational waves.
4.Compact Master equation and Heun’s equation
We begin by looking for solutions of equation (14) that are separable into products:
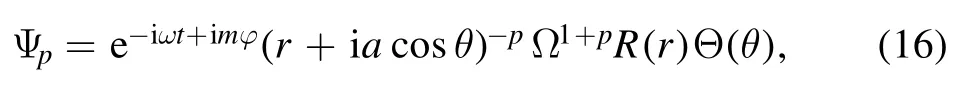
where ω and m are constants.The radial part R(r)and angular partΘ(θ), respectively, satisfy:

Here λ is separation variable constant.We call equation (17)the radial equation, and equation (18) the angular equation.
4.1.The radial equation
Now,we discuss the radial equation(17).First,we transform a new dimensionless variable [6]:

where

Notice that the event(outer)horizon is at the point x = 1,the Cauchy(inner) horizon is at the point x = 0 and the accelerating horizon is at the point(r3-r4).Second we introduce a new function h(x), defined by:
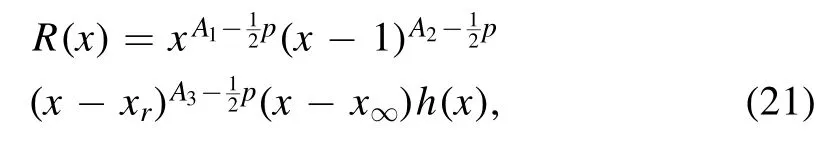
where Aiare constants, given by:
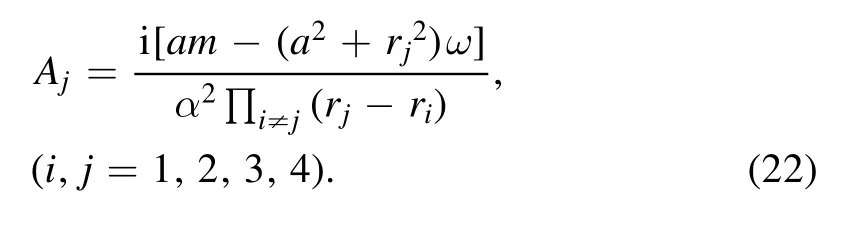
Using equation (21), we find that (x-x∞) is eliminated and the function h(x) obeys the Heun’s equation:
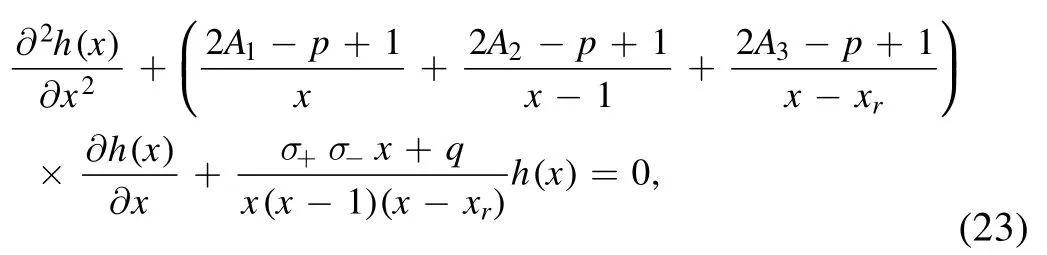
where
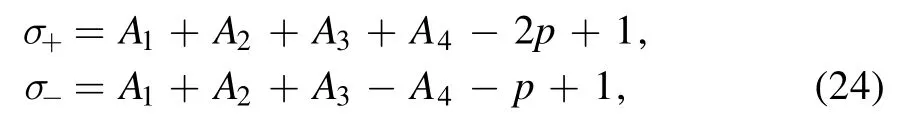
and
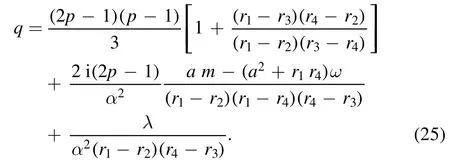
4.2.The angular equation
Under the basis of transformation (4), we should make the other coordinate transformation as follows [6]:

with

We introduce a new functionf(ξ)by a multiplication of Powers of the following form:
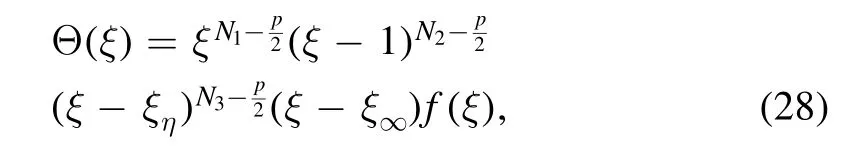
where
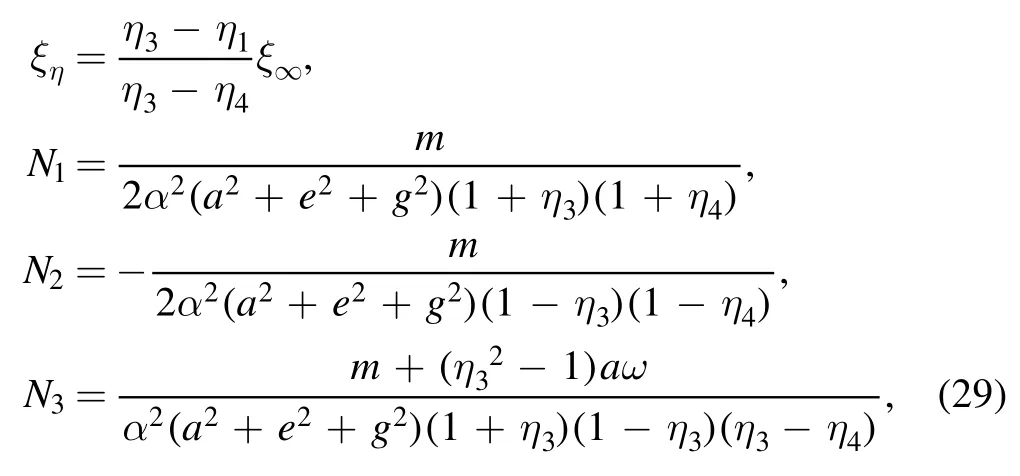
here we useη1= -1andη2= 1.
Then,fξ() satisfies Heun’s equation:
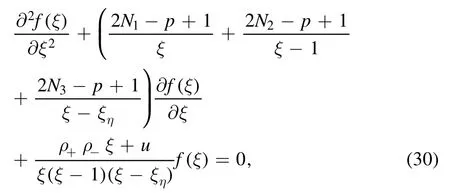
where
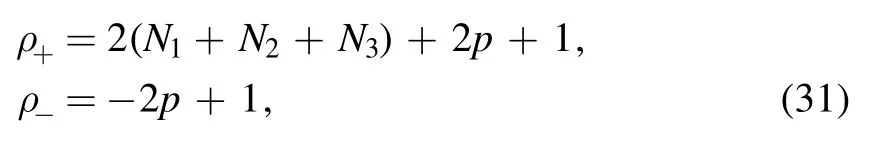
and
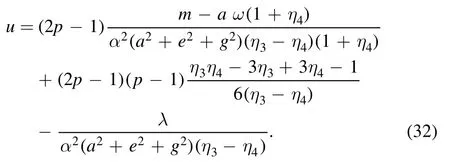
We conclude that each equation, whether radial and angular,is an Heun’s equation in disguise.Therefore,we can use known techniques to analyse solutions.
5.Approximate solutions of radial equation
The solutions of the Heun’s equation are Heun functions,which can usually be written as the form of a series of hypergeometric functions.We turn now to approximate solutions of the differential equation(23).For this purpose,it is convenient to rewrite the function h(x) in the form [20]:
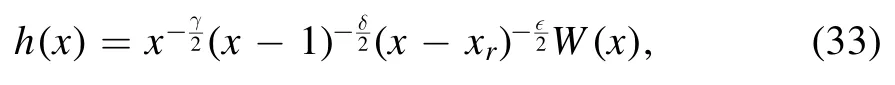
where
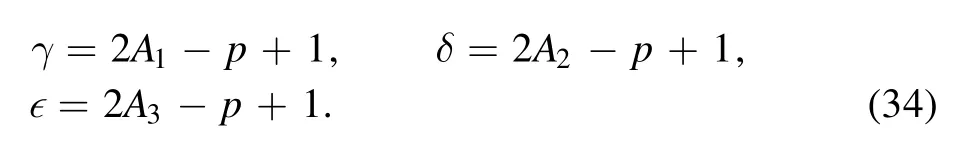
Then we can obtain the normal form of Heun’s equation[20]:
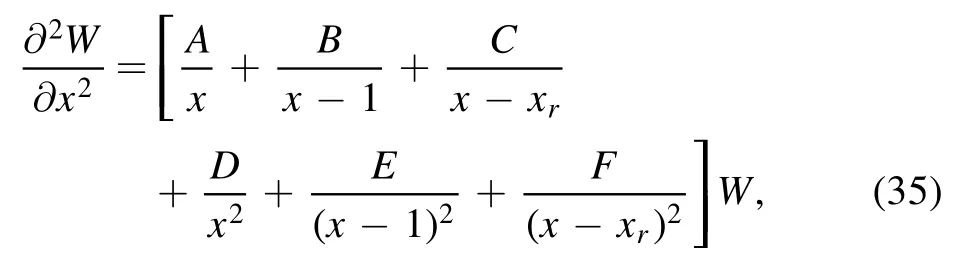
where
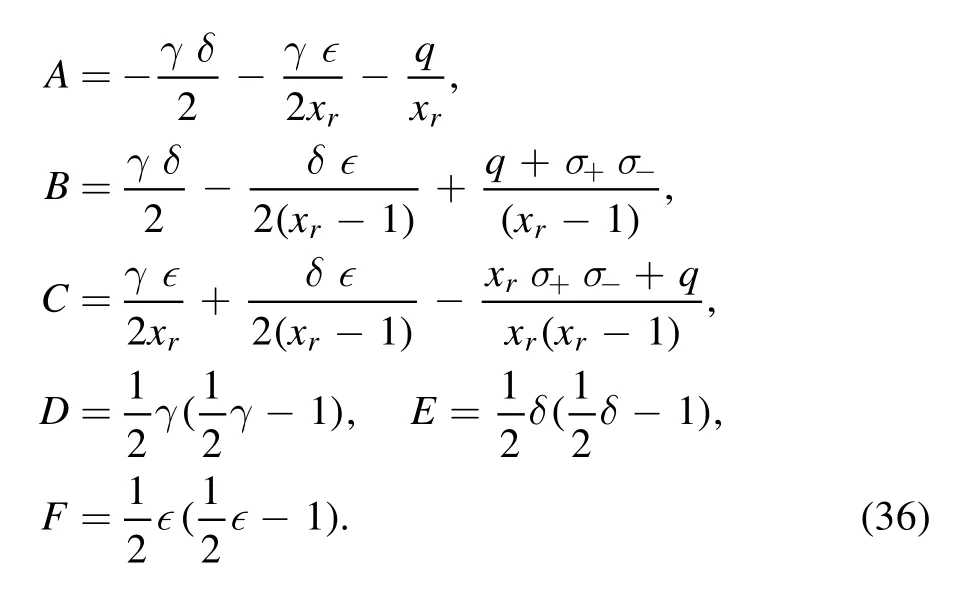
Now we try to make an approximation at event horizon x = 1.Using the Taylor formula, we expand termsat this point:

In the neighbourhood of the event horizon, we can neglect terms which contain(x- 1).Then we can transform the equation (35) into:
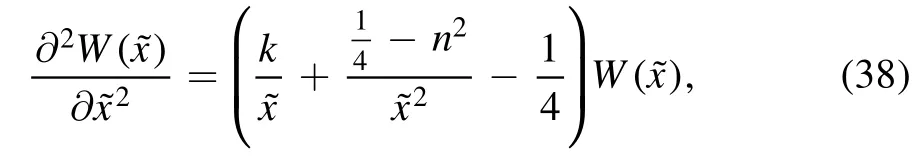
where
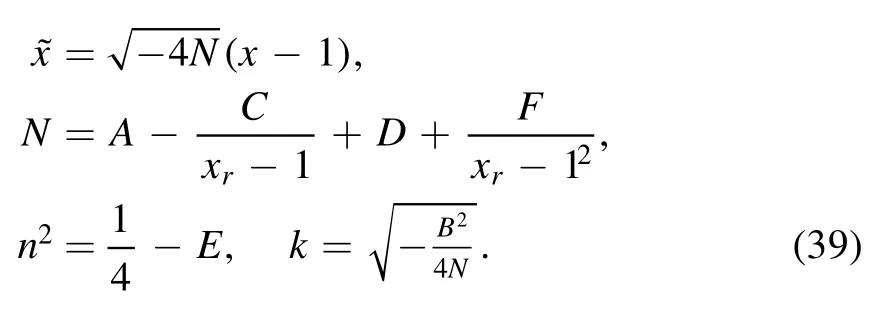
This equation has the solutions of hypergeometry functions which called the Whittaker functions.Two linearly independent solutions of equation (38) can be written by Whittaker
functionsMk±,n[20]:
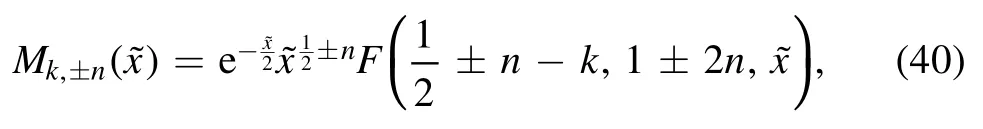
where2nis not integer.
Then we can get two solutions of radial wave equation in the neighbourhood of event horizon:
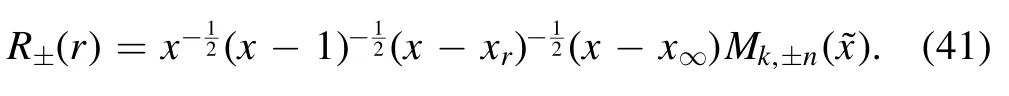
These two equations have the parameters n and k which both including p, so we can compare the gravitational waves and waves of other spins by using the equation (41).
6.Final remarks
In this paper, we derive a compact master equation in accelerating Kerr-Newman space-time.The master equation includes gravitational waves and other waves of massless fields of the spinss≤ 2, so it can be used to compare dynamics properties of waves of perturbing massless spin fields.The Heun’s equation is closely related to master equation.We also obtain approximate solutions which could describe massless spin fields near horizon.The approximate solutions have the parameter p describing a different spin, so it is helpful to study the gravitational waves and it’s analogues.
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant No.11 475 148.
ORCID iDs
 Communications in Theoretical Physics2021年10期
Communications in Theoretical Physics2021年10期
- Communications in Theoretical Physics的其它文章
- Three-dimensional massive Kiselev AdS black hole and its thermodynamics
- Examination of n-T9 conditions required by N=50, 82, 126 waiting points in r-process
- Scalar one-loop four-point integral with one massless vertex in loop regularization
- Strange quark star and the parameter space of the quasi-particle model
- Improved analysis of the rare decay processes of Λb
- A universal protocol for bidirectional controlled teleportation with network coding
