Nonlinear vibration of iced cable under wind excitation using three-degree-of-freedom model?
Wei Zhang(張偉),Ming-Yuan Li(李明遠(yuǎn)),Qi-Liang Wu(吳啟亮),and An Xi(襲安)
1Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures,Beijing University of Technology,Beijing 100124,China
2College of Mechanical Engineering,Beijing University of Technology,Beijing 100124,China
3School of Artificial Intelligence,Tiangong University,Tianjin 300387,China
4The Fifth Electronic Research Institute of MIIT,Guangzhou 510610,China
Keywords:iced cable,wind excitation,galloping,chaotic motion
1.Introduction
The nonlinear statics,dynamics,and stability of cables have received considerable attention due to their extensive applications in the engineering field.High-voltage transmission lines are a flexible cable structure widely used in transmission engineering due to their ability to conduct power over long distances.Cable dynamics have a rich history,which has been summarized in the review articles by Irvine and Caughey,[1]Starossek,[2]and Rega and Ibrahim.[3–5]Among all the different types of cable structures,the suspended cable is a fundamental type used in theoretical studies,and exhibits various dynamic phenomena as a prototype model in applied mechanics.
The nonlinear dynamic responses of elastic suspended cables due to finite vibration amplitudes have received considerable research attention,as suspended cables exhibit a variety of phenomena due to their high flexibility and low damping characteristics.Perkins[6]derived a continuum model that describes the nonlinear,three-dimensional response of an elastic cable to tangential oscillations of one support.A twodegree-of-freedom approximation was used to examine the coupled in-plane and out-of-plane response.Additionally,a four-degree-of-freedom model was developed from the continuum equations by Benedettini et al.,[7]and is able to capture the main phenomena that are likely to occur in the nonplanar finite dynamics of an elastic suspended cable subjected to external force and support motion.Gattulli et al.[8]used analytical and finite element models to study the modal interactions in both planar and spatial responses to harmonic in-plane and out-of-plane loads.Luongo et al.[9,10]derived a nonlinear model of a twisted cable and studied the effect of the twist angle on the nonlinear galloping of suspended cables.Luongo et al.[11]also established a nonlinear two-degree-of-freedom model to describe a flexible elastic suspended cable undergoing galloping oscillations.Kim and Perkins[12]investigated the resonant responses of suspended elastic cables driven by a steady current.Srinil and Rega[13]presented a model formulation capable of reflecting the large-amplitude free vibrations of a suspended cable in three dimensions.Based on a multidegree-of-freedom model,numerical procedures were implemented to solve both spatial and temporal problems.Zhao and Wang[14]investigated the nonlinear responses of suspended homogeneous elastic cables with low initial sag-to-span ratio in the case of 3:1 internal resonance by considering the vertical load.Casciati and Ubertini[15]considered the nonlinear vibration of shallow cables equipped with a semi-active control device.Abdel-Rohman and Spencer[16]studied the along-wind and across-wind responses of suspended cables.Zheng et al.[17]investigated the super-harmonic and internal resonance characteristics of a viscously damped cable with nearly commensurable natural frequencies via a novel method.Chang et al.[18]studied the nonlinear interaction of the first two inplane modes of a suspended cable with a moving fluid along the plane of the cable.Ouni and Kahla[19]investigated the nonlinear dynamics of a cable under first-and second-order parametric excitations.Zhao et al.[20,21]investigated the approximate series solutions of nonlinear free vibrations of suspended cables via the Lindstedt–Poincar′e method and the homotopy analysis method.
Owing to the combination of quadratic and cubic nonlinearities,suspended cables exhibit various planar and nonplanar internal resonance conditions.Srinil et al.[22]and Srinil and Rega[23]conducted an analytical investigation of resonant multimodal dynamics resulting from 2:1 internal resonance in the finite-amplitude free vibrations of horizontal/inclined cables.Nayfeh et al.[24]investigated the nonlinear,nonplanar responses of suspended cables subjected to external excitation.Lacarbonara and Rega[25]investigated 1:1,2:1,3:1,and internal resonances in undamped,unforced,one-dimensional systems with arbitrary linear,quadratic,and cubic nonlinearities for a class of shallow symmetric structural systems.Kamel and Hamed[26]studied the nonlinear behavior of an elastic cable subjected to harmonic excitation.Rega et al.[27]studied an experimental model of an elastic cable carrying eight concentrated masses and hanging from in-phase or out-of-phase vertically-moving supports.Zhang and Tang[28]investigated the chaotic dynamics and global bifurcations[29–31]of a suspended elastic cable under combined parametric and external excitations.Considering 1:1 internal resonance,Abe[32]investigated the accuracy of nonlinear vibration analyses of suspended cables that possess quadratic nonlinearity and cubic nonlinearity,respectively.By the Galerkin method,Huang et al.[33]derived the governing equations describing the motion of a coupled suspended cable-stayed beam structure,and studied its 1:2 internal resonance.Taking into account the bending stiffness,Kang et al.[34,35]systematically investigated the linear and nonlinear dynamics of a suspended cable.
Considering the effect of the geometric nonlinearity of the cable on the coupled behavior between the modes of the beam and cable,Wei et al.[36]developed and investigated a model of the cable-stayed beam system.Wu and Qi studied the dynamic responses of an iced suspended cable were investigated[37]by the finite element method.Jing et al.[38]proposed a numerical model of a wind-loaded two-dimensional(2D)cable,and analyzed the vibration responses induced by rain-wind.The bases of the flow behavior and phenomena existing during 2D airflow were explained by Gorski et al.[39]to analyze the motions of an ice-accreted bridge cable.Via the use of the optimal equivalent control algorithm,Zhao et al.[40]studied a method of controlling the vibration responses of a stay cable.Chang et al.[41]reported experimental results of the mechanism and mitigation of the vibrations of stay cables under rainwind load.Electromagnetic inertial mass dampers were considered by Li et al.[42]to experimentally and analytically study the vibration mitigation of stay cables.
In recent years,some investigations of suspended cable models and research methods have been updated.Using the method of multiple scales,Huang et al.[43]developed a new nonlinear partial differential equation to investigate a suspended cable-stayed beam structure by considering the finite deformations of the structure and the initial configuration of the main cable.Ahmad et al.[44]established an analytical model of a hybrid system composed of two parallel taut cables interconnected by a transverse linear flexible cross-tie.Ishihara and Oka[45]studied the aerodynamic coefficients of a single bundled iced suspension cable and four bundled iced suspension cables for comparison with the results of a wind tunnel test.Akkaya and Horssen[46]described a model of the rain-wind-induced oscillations of an inclined cable.Based on the mode superposition method with enhanced shape functions,Javanbakht et al.[47]proposed a control-oriented numerical model to evaluate the dynamic response of a stay cable.Li et al.[48]established a generalized gust loading model for predicting the buffeting response,which is applicable to both small-aspect-ratio and long-span,line-like bridges.Guo et al.[49]proposed an elastic cable-rigid body coupled model to investigate the dynamic interaction between the torsional dynamics of the boundary tower and the nonlinear transversal vibrations of the cables.According to catenary theory,Mansour et al.[50]studied the free undamped vibration of a suspension cable with arbitrary sag and inclination.Zhao et al.[51,52]investigated the influence of the temperature on the vibration characteristics of suspension cables related to the excitation amplitude and sag-to-span ratio,and the results revealed that temperature variation gave rise to qualitative and/or quantitative changes of the nonlinear vibration properties.
The present study focuses on the complex nonlinear vibrations of a three-degree-of-freedom iced cable.The influences of the support displacement and wind excitation on the nonlinear dynamic responses of the system are analyzed.Considering the galloping of the suspended structure under transverse wind,a nonlinear dynamic model of the three-degree-offreedom iced cable is established.The nonlinear partial differential equations of motion for the iced cable are established via Hamilton’s principle.Additionally,the dimensionless differential equations of motion are obtained and reduced into a set of nonlinear ordinary differential equations by the Galerkin method.[53,54]With the assistance of the method of multiple scales,the averaged equations of the system in the presence of principal parametric resonance?1/2 subharmonic resonance and 2:1 internal resonance are obtained.According to the averaged equations,the numerical results including bifurcation diagrams,waveforms,phase plots,and frequency spectrum are obtained to investigate the intrinsically nonlinear behaviors of the iced cable.It is demonstrated that the iced cable exhibits alternating periodic and chaotic motions according to the influences of the nonlinear factors.
2.Theory and formulation
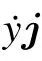

Fig.1.Model of iced cable.

Considering the interception of a small section of the iced cable for centralized mass,the center of mass of the line lies on the origin O.In the Cartesian coordinate(oxy)system,the vertical coordinate of the center of mass is y.For a wind speed Vm,the relative velocity is Vr=Vw?
then the angle of attackαwill be

Because the cross-section of the iced cable is a non-circular irregular shape,the gust of the suspension produces not only a resistance Fdin the Vrdirection,but also a lift FLand a torsional force Fwthat are perpendicular to it.According to the aerodynamic principle,the following equations can be obtained:
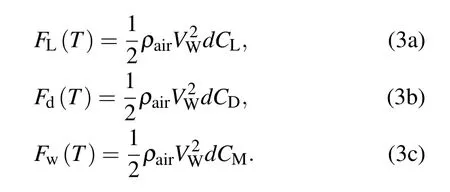
The tangential force and normal force of the cable are respectively
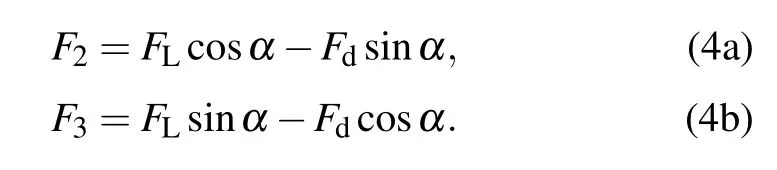
Because the model considers low-frequency vibration,the value ofαis very small;thus,the following approximate expressions can be held:
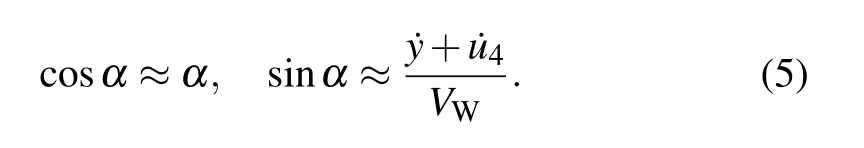
By substituting Eqs.(2),(3),and(5)into Eq.(4),the effects of the wind along the cable in the tangential,normal,and rotational directions of the component can be calculated,respectively,as
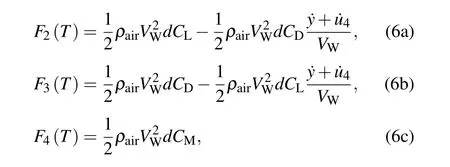
where d is the maximum dimension of the aerial surface of the cable,and CL,CD,and CMare respectively the lift,drag,and torsional coefficients,which are the functions of the crosssectional shape and the angle of attack.
According to Hamilton’s principle,

whereΠT,ΠS,andΠWare the kinetic energy,strain energy,and external force work,respectively.The equations of motion can be obtained by applying Hamilton’s principle as follows:
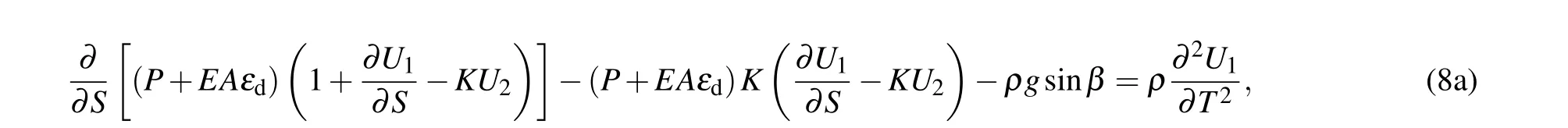

The boundary conditions of the cable are given as

The tension and curvature expressions are respectively
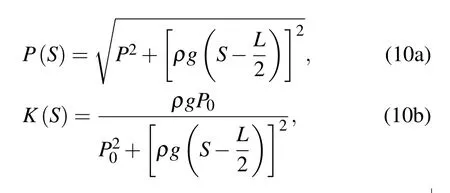
where

Equation(11)shows that when the sag-to-span ratioD/H≤1/8,P0≥ρgL.By taking the Taylor expansion of Eq.(10),the following equation is obtained:
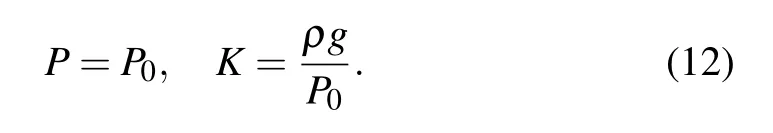
The dimensionless curvature is k=KL=ρgL/P0,and can be regarded as a small perturbation parameter.By expanding Eq.(8)and omitting k2and higher-order terms,the dynamic equations of small sag are obtained as follows:

To obtain the dimensionless governing equation of motion,the transformations of the variables and parameters are introduced as


Substitution of these parameters into Eq.(13)yields the following equations:

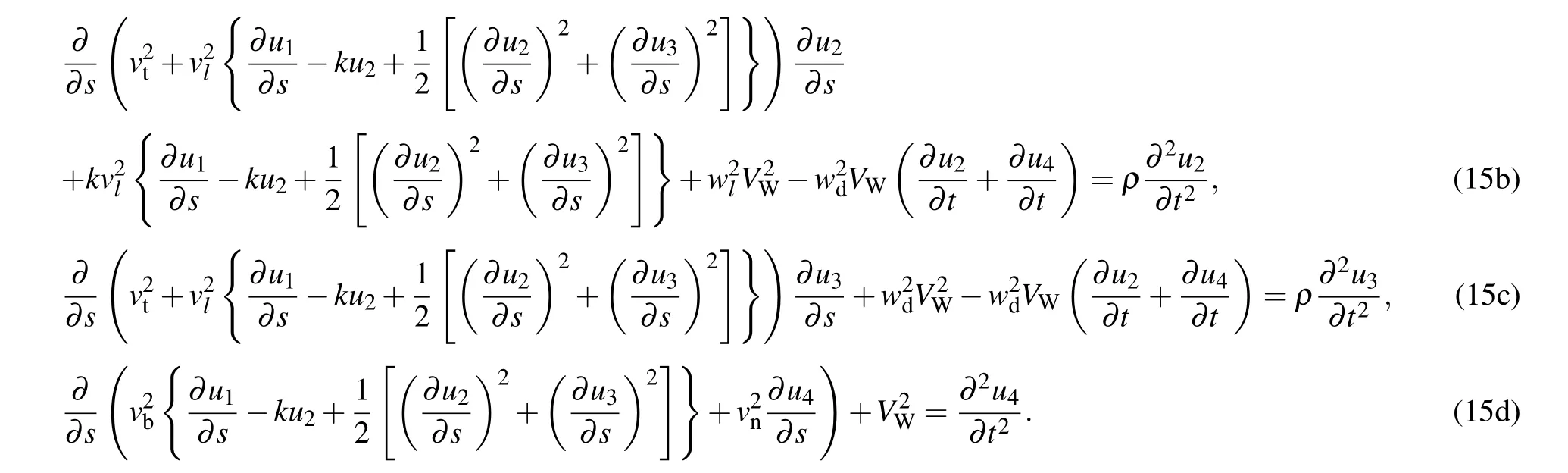
Because the vibration in the tangential direction of the suspension cable does not play a major role,the vibration in the L1direction is ignored,which yields

therefore,
where

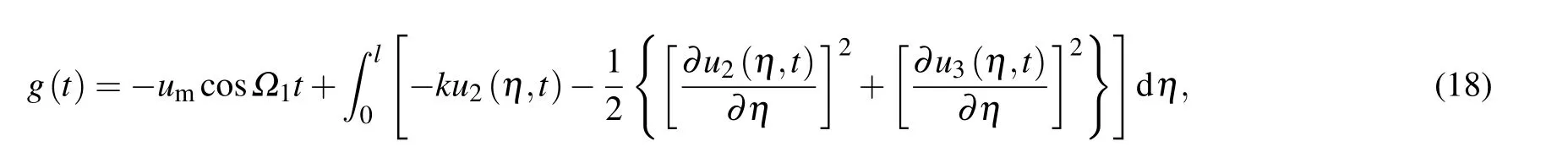

Substitution of Eq.(17)into Eq.(15)yields the following equations:

The boundary conditions are given as
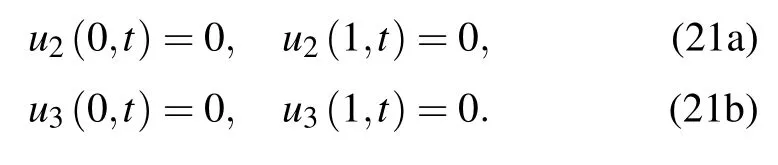
The Galerkin method is used to separate the variables,and the partial differential equations are then transformed into ordinary differential equations:
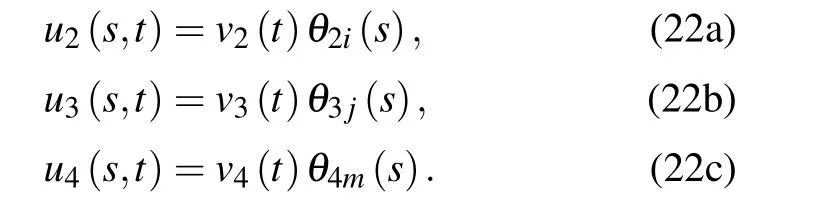
The in-plane vibration mode is as follows:

with
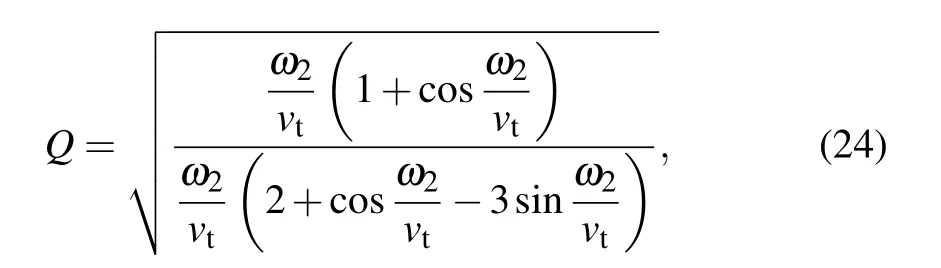
whereωis determined by the following characteristic equation:

The out-of-plane vibration mode is as follows:

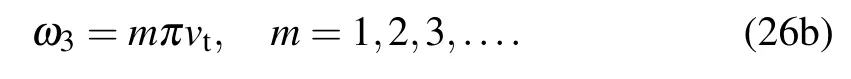
The torsional mode is

By applying the Galerkin procedure to the dimensionless governing differential equation of motion,i.e.,by substituting Eqs.(22)–(27)into Eq.(20),the three-degree-of-freedom ordinary differential equations of the cable motion are obtained as follows:

Equation(28c)is a linear differential equation,and equations(28a)and(28b)are uncoupled.Therefore,the solution of Eq.(28c)can be substituted into the other two equations,thereby reducing the three-degree-of-freedom governing equation into a two-degree-of-freedom governing equation.According to the theory of forced vibration,the solution of Eq.(28c)yields

where

Substitution of Eqs.(29)and(30)into Eqs.(28a)and(28b)yields the following equations:

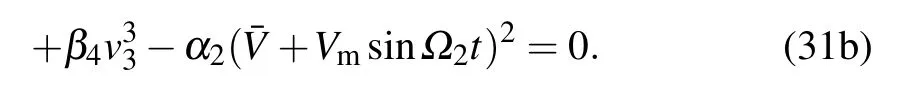
By substituting the one-term expansion

into Eq.(31)and equating the coefficient of the harmonics to zero,an algebraic equation relating the frequencyωwith the amplitudes A1and A2can be obtained.
3.Analysis of amplitude–frequency property
The introduction of a small perturbation parameterεinto Eq.(31)yields the following equations:

By the method of multiple scales,the following equations are obtained:
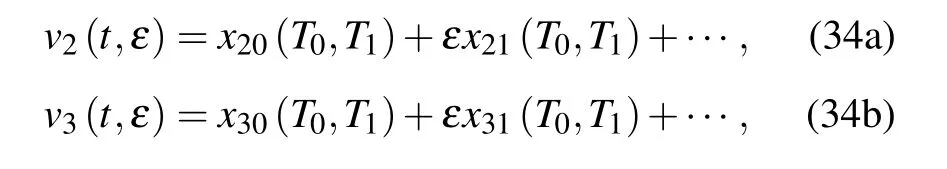
where T0=t and T1=εt.
The differential operator is
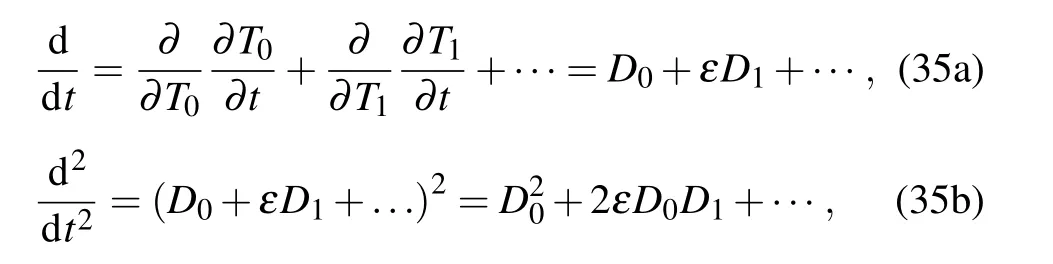
where Dk=?/?Tkand k=0,1,...
Considering the case of principal parametric resonance,i.e.,1/2 subharmonic resonance and 2:1 internal resonance,the following expressions are obtained:

whereσ1andσ2are two detuning parameters,andΩ1=2.0.
By substituting Eqs.(33)–(35)into Eq.(32),the following equations are obtained:The polar form solution of Eq.(36)is



Substitute Eq.(39)into Eq.(38)and let the secular term be zero,then the following equations will be yielded:

The averaged equation in the polar form of the iced suspended cable is derived as

Let A2and A3be denoted in the following forms:
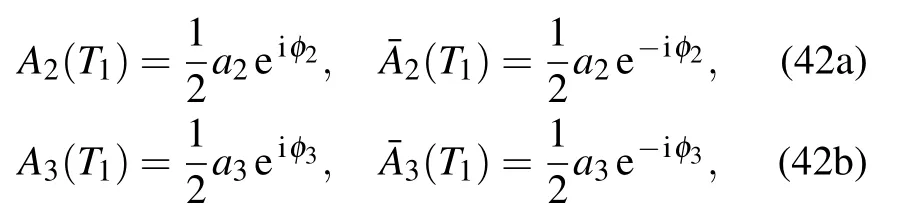
and substitute Eq.(42)into Eq.(41)and separate the real part and imaginary part,then the averaged equation in polar form will be obtained below.
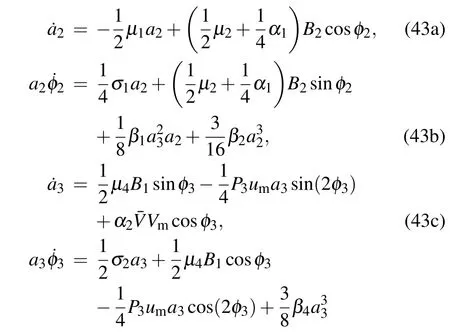

By equating the coefficients of sine and cosine in Eq.(43)to zero,the relationship between the amplitude–frequency characteristics is obtained as follows:

To study the complex dynamics of the iced cable,the amplitude–frequency characteristics curves of system(31)are analyzed.However,the analytical solutions of system(31)are very difficult to obtain;therefore,the following two special cases are considered:
(i)the two modes are weakly coupled;
(ii)the two modes are strongly coupled.
For case(i),assume a3=1 in Eq.(44a)and a2=1 in Eq.(44b),then the amplitude–frequency relationship of the weakly coupled system will be expressed as

Figures 2 and 3 respectively present the amplitudes a2and a3versus detuning parameterσ1and B2under different values of damping coefficientμ1.The results demonstrate that the increase of the damping coefficientμ1will lead to the decrease in the amplitudes a2and a3.Moreover,figures 2 and 3 present the hardening properties of the stiffness and jump phenomenon of the amplitude based on the amplitude–frequency curve.

Fig.2.Weak coupling amplitude–frequency(a)A1 and(b)A2 versusσ1 under different damping coefficients.

Fig.3.Weak coupling amplitude–frequency(a)A1 and(b)A2 versus B2 under different damping coefficients.
For case(ii),assume a3=2 in Eq.(44a)and a2=2 in Eq.(44b),then the strongly coupled system will be obtained as follows:


Fig.4.Strong coupling amplitude-frequency(a)A1 and(b)A2 versusσ1 under different damping coefficients.
Figures 4 and 5 respectively present the amplitudes a2and a3versus detuning parametersσ1and B2under different values of damping coefficientμ1.Like case(i),with the increase of the damping coefficientμ1,the amplitudes a2and a3decrease.In addition,with the constant change of parameters,the amplitude of the system will present a jump phenomenon.It can be seen that the amplitudes in case(ii)are larger than those in case(i),which is due to the differences between the two cases.

Fig.5.Strong coupling amplitude–frequency(a)A1 and(b)A2 versus B2 under different damping coefficients.
4.Numerical simulations of periodic and chaotic motions
Numerical simulations are performed to determine the periodic motion and chaotic motion of the iced suspended cable.The numerical integration of Eq.(31)is performed by using the Runge–Kutta algorithm with variable precision∈[0.0001,0.01].[38]More specifically,the transient effects are avoided by dropping the first 60% of the simulating time:2000 s.The excitation V is a main controlling parameter in the research of the nonlinear dynamic behaviors of cables,and is selected as the controlling parameter to discover the complicated nonlinear dynamics.The parameters are set to be as follows:E=0.9×1011Pa,G=0.4×1011Pa,g=9.8 N/kg,L=400 m,ρ=0.92 kg/m,ρair=1.2 kg/m3,R=10×10?3m,and um=1 m.
In this section,the emphasis is placed on the influence of external excitation on the motion of a three-degree-of-freedom iced suspended cable structure.The horizontal wind speed V is taken as the control parameter.The amplitude of the wind speed pulse is constant,and the amplitude umof the bearing motion is assumed to be a constant value.The dependence of the three-degree-of-freedom iced cable on the horizontal wind speed V is investigated.Considering the parametric and external excitation on the iced cable,there exist abundant dynamic behaviors.The dynamic motions of the iced cable under different wind speeds are calculated based on the torsional vibration of the three-degree-of-freedom system which occurs in a single cycle.Table 1 exhibits the typical examples of the motion forms of the iced cable under different wind speeds.The bifurcation diagrams of the two degrees of freedom v2and v3versus wind speed V are presented in Figs.6(a)and 6(b),respectively and figure 6(c)shows the largest Lyapunov exponent of v2.When V∈[0.78,0.88],V∈[1.36,1.75],and V>1.9,the system exhibits the typical characteristics of chaotic motion.

Table 1.Typical examples of motion forms of iced cable under different wind speeds.
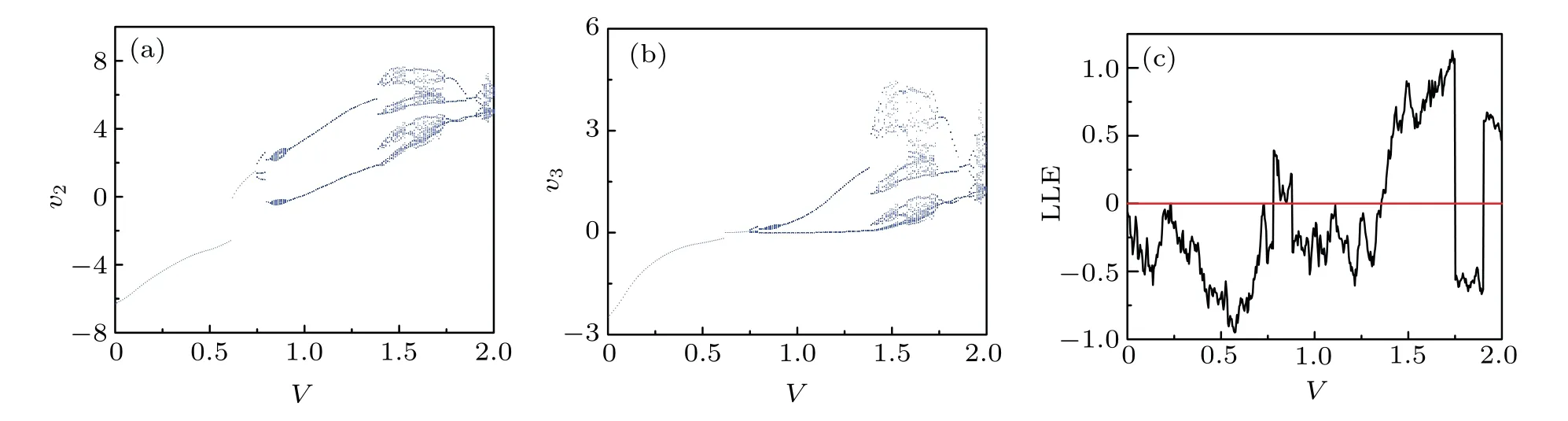
Fig.6.Bifurcation diagram of v2 and v3 under different values of wind speed V1.

Fig.7.Periodic motion of iced cable obtained when V=0.83 m/s.

Fig.8.Multi-periodic motion of iced cable obtained when V=0.94 m/s.

Fig.9.Chaotic motion of iced cable obtained when V=1.17 m/s.
In each of Figs.7–9,panels(a)and(c)respectively show the phase portraits on the planes(v2,˙v2)and(v3,˙v3),panels(b)and(d)respectively represent the waveforms on the planes(t,v2)and(t,v3),and panels(e)and(f)respectively display the three-dimensional phase portrait in space(v2,˙v2,v3)and the frequency spectrum on plane(frequency,v2).It should be noted that the frequency spectrum can be used to distinguish between periodic motion and chaotic motion.The results reveal that there exist one-periodic motion(Fig.7),multiperiodic motion(Fig.8),and chaotic motion(Fig.9)when the system is under the action of different resonance mechanisms,including in-plane parametric resonance and out-of-plane superharmonic resonance.Moreover,the displacement of the vibration is found to be enhanced with the increase of the wind speed.
5.Conclusions
In this paper,the theory of nonlinear dynamics is used to investigate the wind-excited vibration response of an iced suspended cable.The effects of the system under both external and parametric excitation are investigated.Using Hamilton’s principle,a dynamic model of a three-degree-of-freedom iced suspended cable is first established.Then,the approximate equation in the case of small sag is derived,as shown in the dimensionless equation.The amplitude–frequency characteristics are obtained using the harmonic balance method.The perturbation equation is analyzed using the method of multiple scales,and the averaged equation is derived and used to capture the behaviors of the system under the action of inplane parametric resonance and out-of-plane superharmonic resonance.Based on the numerical simulation,the nonlinear vibration responses of the iced cable under parametric excitation and external excitation caused by horizontal wind are determined.The numerical results reveal that the iced suspended cable presents a periodic motion,multi-periodic motion,and chaotic motion under in-plane parametric resonance and out-of-plane main resonance.It is found that with the increase of the wind speed,the behavior of the system changes from a one-periodic motion into a multi-periodic motion,and finally into a chaotic motion.Compared with the results of a two-degree-of-freedom iced suspended cable,the effect of torsional vibration on the system cannot be neglected.Furthermore,theoretical analysis reveals that the vibration of the iced cable can be effectively controlled,which could be a useful technique to ensure the safety of the cable structure.
——張偉
- Chinese Physics B的其它文章
- Origin of anomalous enhancement of the absorption coefficient in a PN junction?
- Protection of isolated and active regions in AlGaN/GaN HEMTs using selective laser annealing?
- First-principles study of plasmons in doped graphene nanostructures?
- Probing thermal properties of vanadium dioxide thin films by time-domain thermoreflectance without metal film?
- An improved model of damage depth of shock-melted metal in microspall under triangular wave loading?
- Signal-to-noise ratio of Raman signal measured by multichannel detectors?

