Multiple Sign-Changing Solutions for Quasilinear Equations of Bounded Quasilinearity
Jiaquan Liu,Xiangqing Liuand Zhi-Qiang Wang
1 LMAM,School of Mathematical Science,Peking University,Beijing 100871,China
2 Department of Mathematics,Yunnan Normal University,Kunming,Yunnan 650500,China
3 College of Mathematics and Informatics and Center for Applied Mathematics of Fujian Province(FJNU),Fujian Normal University,Fuzhou,Fujian 350117,China
4 Department of Mathematics and Statistics,Utah State University,Logan,UT 84322,USA
Abstract. The existence of an infinite sequence of sign-changing solutions are proved for a class of quasilinear elliptic equations under suitable conditions on the quasilinear coefficients and the nonlinearity
Key Words: Quasilinear elliptic equations, sign-changing solution, an elliptic regularization method.
1 Introduction
In this paper,we study the existence of sign-changing solutions for the following quasilinear elliptic equation
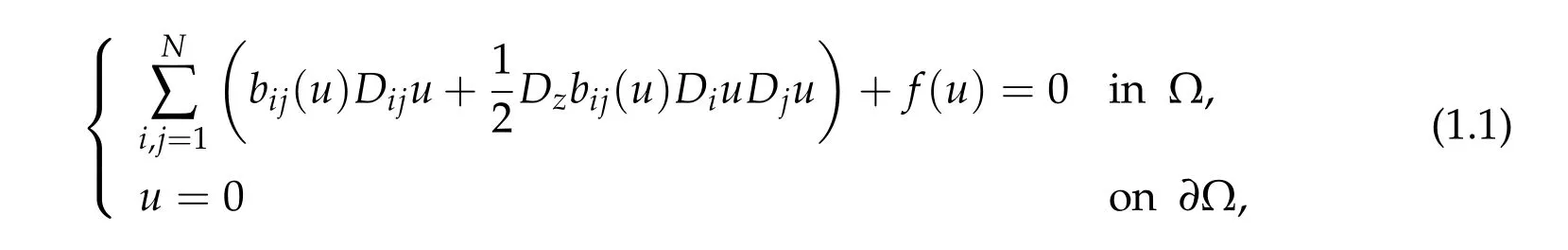
where Ω?RNis a bounded domain with smooth boundary,and we use the notations


(b2) There exist constantsq>2,δ>0 such that

(b3) There exists a positive constantcsuch that

(b4)bij(z)is even inz.
(f1) Letf ∈C(R,R)satisfy that there exist constantsc>0 andr ∈(2, 2?)such that

(f2) There exists a positive constantcsuch that

(f4)f(z)is odd inz.
For simplicity of notations we use the samecto denote some constants in the above conditions.
We are looking for weak solutions for Eq.(1.1),namely a functionu ∈H10(Ω)∩L∞(Ω)satisfying
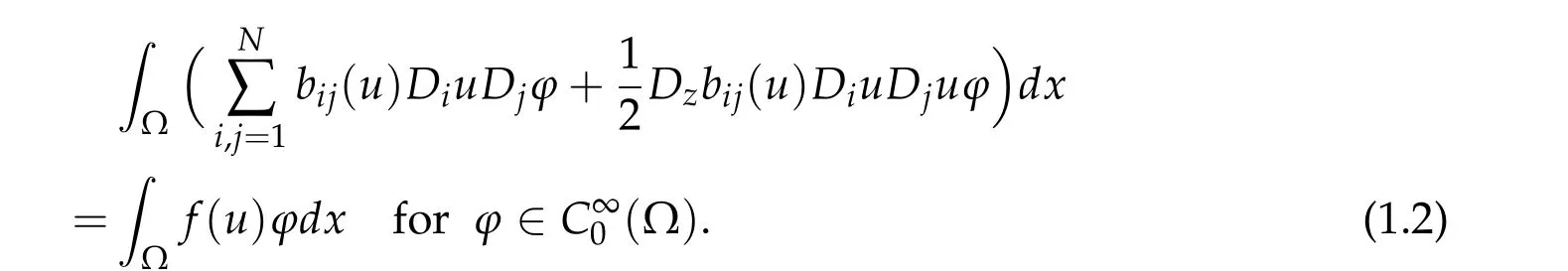
For semilinear case, this is in the setting of the classical superlinear problems that goes back to the celebrated paper of Ambrosetti and Rabinowitz [1] (see also the book [24])in which infinitely many solutions were obtained using the symmetric mountain pass theorem. Later a sequence of sign-changing solutions were assured to exist in the setting[4,13].
The following is the main result of this paper which establish the above mentioned results for the case of bounded quasilinearity.
Theorem 1.1.Assume(b1)-(b4),(f1)-(f4). Then Eq.(1.1)has infinitely many sign-changing solutions.
Formally the problem has a variational structure,given by the functional

The functionalIis continuous, but not differentiable onH10(Ω). Historically there have been several approaches developed for handling this type of non-smooth variational problems. The critical point theory for nonsmooth functionals has been established,see[2,3,8,10,11,15]. The authors of the present paper developed a new approach in[16,17,20,21], by introducing ap-Laplacian perturbation. The theory in the above papers were used in[16]to treat the existence of an infinite sequence of sign-changing solutions for a problem similar to Eq. (1.1) but having a quasilinear termbijof power growth inu. For some technical reasons, thep- Laplacian perturbation approach does not work well for the case we consider here,namely the quasilinear termbijis bounded. The existence of a nontrivial solution for (1.1) was given in[2,8]. The question on the existence of sign-changing solutions in particular on whether there exist an infinite sequence of sign-changing solutions in this case was left open in[8,16].
In this paper we will use a different approach which was used in[22]where localized solutions for semiclasscial Schr¨odinger type equations were considered. We outline the approach here first. Instead of introducing ap-Laplacian perturbation, we truncate the quadratic form ∑Ni,j=1bij(u)DiuDju. Under suitable truncations, up to some level sets controlled by the truncation,the resulting problem share critical points with the original problem. More precisely,letμ>0 be a parameter and define a family of functionals

whereσ>0 is fixed satisfying

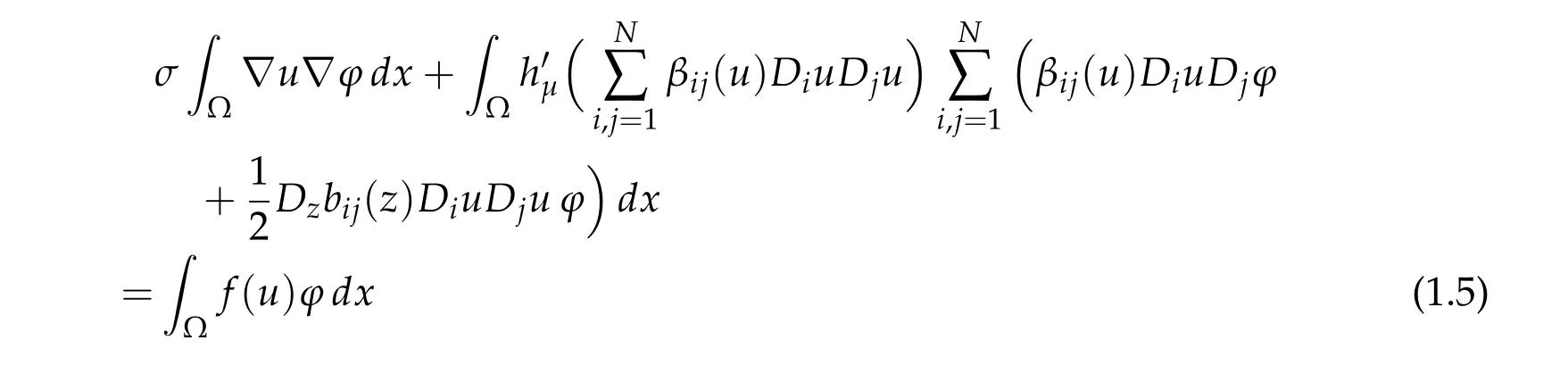

We will verify thatIμis aC1-functional onH10(Ω)and satisfies the Palais-Smale condition. The corresponding Euler-Lagrange equation forIμis thenuwill be a solution of the original equation(1.1). Note that no limit processμ →0 is needed for the existence of critical point of the original problem. By taking smallerμwe obtain more solutions of the original problem. This is the main idea of the approach.In order to obtain sign-changing critical points of the functionalIμwe shall apply the method of invariant sets for descending flow, as developed in [6,18,19]. The idea of using invariant sets for descending flow for studying sign-changing solutions goes back to some earlier work for semilinear elliptic boundary value problems,such as in[5,7,9,23]for the existence of sign-changing solutions and [4,13] for an infinite sequence of signchanging solutions.
Throughout the paper,cdenotes various positive constants,cμdenotes constants depending onμ. The paper is organized as follows. In Lemma 2.1 we define the truncation functionhμ. In Lemma 2.2 and Lemma 2.3 we prove the functionalIμis aC1-functional onH10(Ω)and satisfies the Palais-Smale condition. Lemma 2.4 to Lemma 2.8 and Proposition 2.1 are devoted to constructing critical values of the functionalIμby the method of invariant sets for descending flow. In Proposition 2.2 we prove the regularity result as the gradient estimate(1.6),which completes the proof of Theorem 1.1 consequently.
2 Proof of Theorem 1.1
We start with giving the definition of the functionhμused in the truncation for the functionalIto getIμ.


Now define

Then 0≤q(t)≤1,q(t)=1 fort ≤1;q(t)=0 fort ≥Tε;q(t)is decreasing intand


In the future we choose and fixεandT:=Tεin the definition ofhabove such that

Lemma 2.2.The functional Iμ is differentiable and

Proof.LetHμbe the truncated quadratic term inIμ
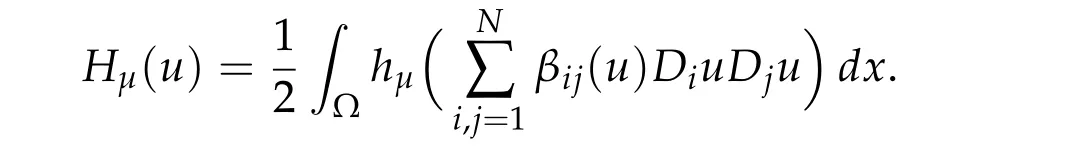
The other two terms inIμare “harmless” to the smoothness. We compute the Gateaux derivative ofHμ. The Gateaux derivative ofHμatuin the direction?is defined as
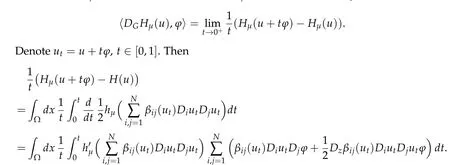
Since
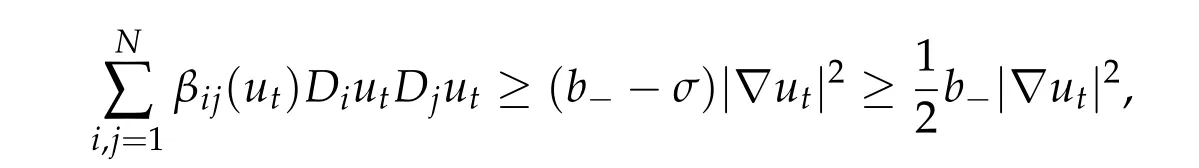
we have

Hence

By Lebesgue’s dominated convergence theorem we have

The Gateaux derivativeDGHμ(u) is a bounded linear functional onH10(Ω). MoreoverDGHμ(u)continuously depends onuand there exists a positive constantcμsuch that
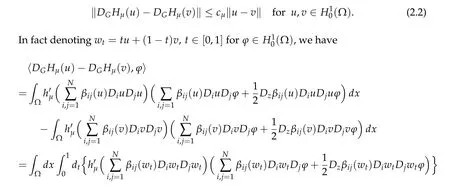

In the above we have used the fact that

Since the Gateaux derivativeDGHμ(u) is a bounded linear functional onH10(Ω) and continuously depends onu,Hμ(u) is Frechet differentiable and the Frechet derivativeDHμ(u)=DGHμ(u). Finally

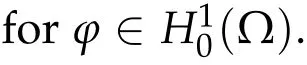
Lemma 2.3.Iμ satisfies the Palais-Smale condition.
Proof.We have

In the above we have used the fact that
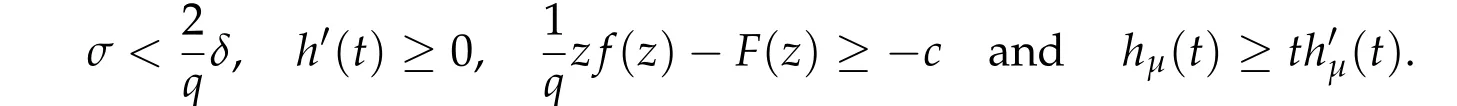
Let{un} ?H10(Ω) be a Palais-Smale sequence ofIμ. By (2.3),unis bounded inH10(Ω).Assumeun ?uinH10(Ω),un →uinLs(Ω)(1≤s< 2?),un(x)→u(x)a.e.x ∈Ω. We have

We estimate the term〈DHμ(un)?DHμ(um),un ?um〉. Assumeu,v ∈H10(Ω). Denote

unis a Cauchy sequence,hence a convergent sequence inH10(Ω).
From the proof of Lemma 2.2 and Lemma 2.3(see(2.2),(2.5)),we have the following lemma,which is useful in our proofs later.
Lemma 2.4.There exist positive constants cμ and c?μ such that

We construct multiple solutions of the approximate problem(1.5),in particular multiple sign-changing solutions by the method of invariant sets for descending flow. The abstract framework is established in [16,18,19,23] generalizing the classical mountain pass theorems without the setting of invariant sets[1,24].
Proposition 2.1.Let X be a Banach space, f be an even C1-functional on X and satisfy the Palais-Smale condition. Let P,Q be open convex subsets of X,Q=?P,W=P ∪Q,W/= ?.Assume there exists an odd map A:X →X satisfying
(A1)Given c0,b0>0there exists b=b(c0,b0)such that if‖D f(x)‖≥b0,|f(x)|≤c0then

(A2)A(?P)?P,A(?Q)?Q.
Let E be a finite-dimensional subspace of X and B be a ball in E centered at the origin. Define

Assume
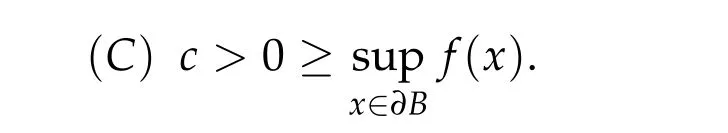
Then c is a critical value of f and
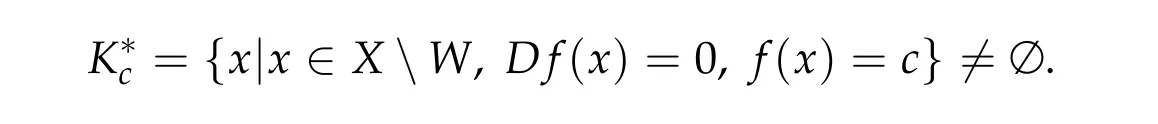
In the following we verify thatIμsatisfies all the assumptions of Proposition 2.1 for a suitable operatorAand subsetsP,QandB. In Lemma 2.2 and Lemma 2.3 we have proved thatIμis aC1-functional onH10(Ω)and satisfies the Palais-Smale condition. Now we define the operatorAand the subsetsP,Qand verify the assumptions(A1),(A2).
Definition 2.1.Given u ∈H10(Ω),define v=Au ∈H10(Ω)by the following equation

where c?μ is the positive constant which appears in Lemma2.4and
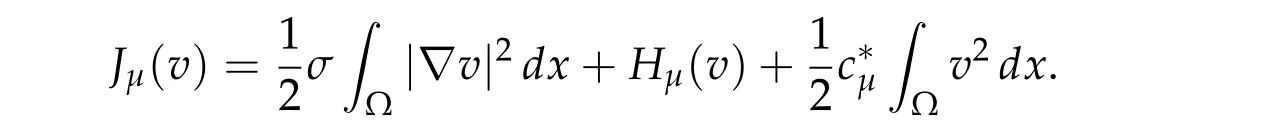
Without loss of generality we assume

Lemma 2.5.The operator A is well-defined and continuous.

We complete the proof.
Lemma 2.6.There exists a constant cμ such that

Moreover

Consequently the assumption(A1)holds.

By Lemma 2.4,we have

Thus,we complete the proof.
We define the open convex setsPandQ,and verify the assumption(A2)of Proposition 2.1.
Definition 2.2.Define the open convex sets P and Q as

where u±= max{±u,0},c?μ is the constant in Lemma2.4,S=Sp(Ω)is the Sobolev constant for the embedding H10(Ω)(Ω),ν>0is a small constant.
Lemma 2.7.There exists a positive constant ν0such that for ν<ν0,it holds that A(?P)?P,A(?Q)?Q.
Proof.Assumeu ∈?Q,v=Au. By the definitions

Choose?=v+as test function in(2.8b). Since
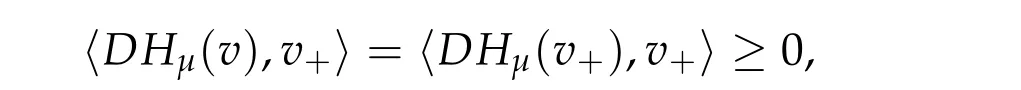
the left hand side of(2.8b)
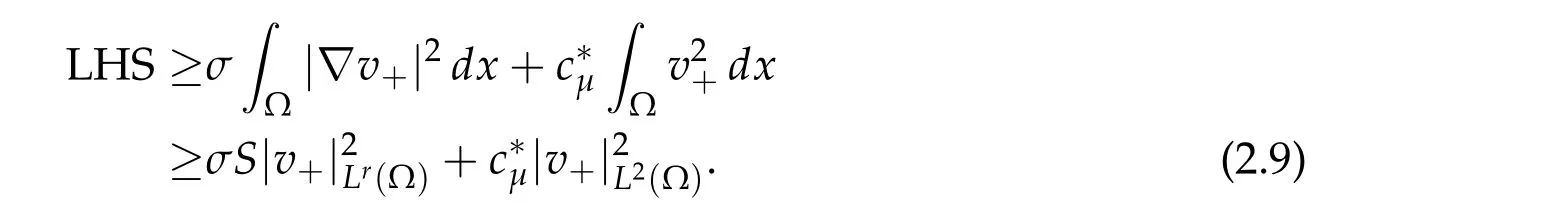
For anyτ>0,by the assumptions(f1),(f3),there existscτ>0 such that

The right hand side of(2.8b),

provided we chooseτandν0such that
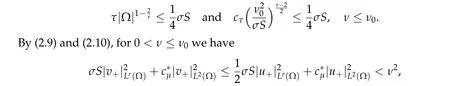
hencev=Au ∈QandA(?Q)?Q. SimilarlyA(?P)?P.
We apply the abstract theorem(Proposition 2.1)to define a sequence of critical values of the functionalIμ,and estimate the bound of the critical values.
Definition 2.3.Let0<λ1<λ2≤··· be the eigenvalues of the Laplacian operator ?Δin H10(Ω)∩H2(Ω),e1,e2,···,be the corresponding eigenfunctions. Denote

where Rl>0satisfies that Iμ(u)≤I(u)<0for u ∈El,‖u‖≥Rl. Define

Lemma 2.8.There exist0<αl<βl,l=2,3,···,such that

Proof.SinceId ∈Γl,we have

By the condition(f1),we can chooseτ>0 such that

Define

By choosingRllarge enough,we can assume

By Lemma 4.5[16]forν0sufficiently small it holds that

Hence

We claim that there exist positive constantsτandc,independent ofμandlsuch that
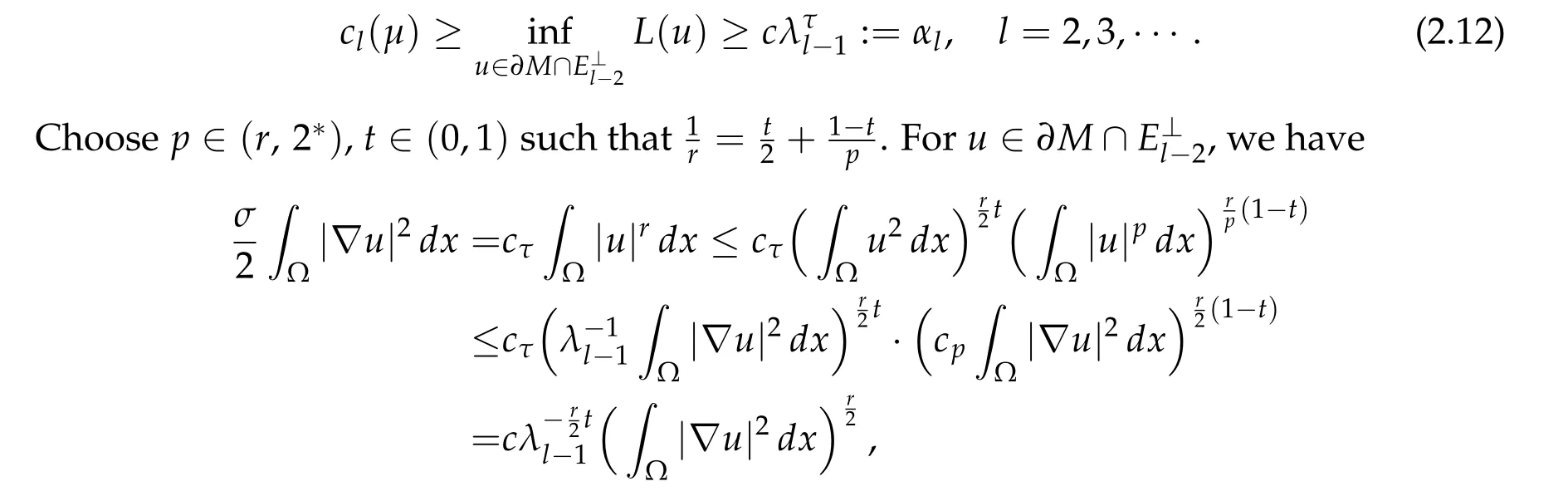
hence

Thus,we complete the proof.
We are in a position to prove Theorem 1.1. To do it,we need the following regularity result for solutions of the quasilinear elliptic equation (2.13), the proof of which will be given in Appendix.
Proposition 2.2.Let u ∈H10(Ω),DIμ(u) = 0and Iμ(u)≤L. Then there exist K> 0,γ ∈(0,1),depending on L only,such that

ulis a sign-changing solution of the original equation(1.1),andI(ul)=Iμl(ul)=cl(μl)≥αl →∞asl →+∞. We obtain infinitely many sign-changing solutions of Eq.(1.1)
Remark 2.1.Without the assumptions(b4),(f4),we have the following theorem of three nontrivial solutions,which is reminiscent of the well known result for semilinear elliptic equations such as in[7,9,23,25].
Theorem 2.1.Assume(b1)-(b3),(f1)-(f3).Then Eq.(1.1)has at least three nontrivial solutions,one is positive,one is negative and the third is sign-changing.
Again we apply the method of invariant sets of the descending flow,see[6,18,19].We leave the detail of proof to the interested readers.
AppendixProposition A.1.Assume u ∈H10(Ω),DIμ(u) = 0and Iμ(u)≤L. Then there exist K> 0,γ ∈(0,1),depending on L only,such that

First we apply Moser’s iteration to obtain theL∞-bound.
Lemma A.1.Assume u ∈H10(Ω),DIμ(u) = 0and Iμ(u)≤L. Then there exists M> 0,depending on L only,such that



By(A.5)and(A.6),we have Starting froms0=d>1,by iteration we obtain

Thus,we complete the proof.
Proof of PropositionA.1.We write down the quasilinear equation (1.1) in the divergence form

Denote
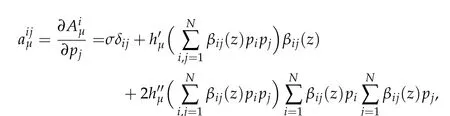
fori,j= 1,···,N. We verify the structure conditions satisfied by the quasilinear equation(Q)by use of the assumptions(B),(F)and the property of the truncated functionhμ.

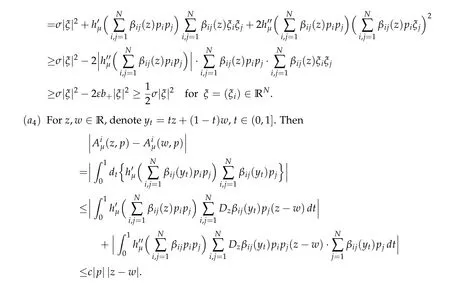
(b) On the other hand,we have

where Λ(M)is an increasing function from R+to R+.
Assumeu ∈H10(Ω),DIμ(u) = 0,Iμ(u)≤L. By Lemma A.1, there existsM=M(L)such that|u|L∞(Ω)≤ M. The quasilinear equation (Q) satisfies the natural structure conditions for elliptic equation. All the assumptions of Corollary 1.5,Theorem 1.7 of[14](see also[12])are fulfilled. Therefore there existK> 0,γ ∈(0,1)depending only onM,Λ such that
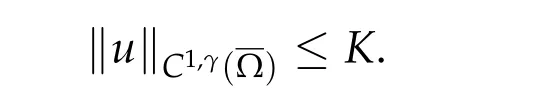
We complete the proof.
Acknowledgements
The authors would like to thank the referee for carefully reading the paper and for helpful suggestions. The work is partially supported by NSFC (Nos. 11761082, 11671364,11771324 and 11831009).
 Analysis in Theory and Applications2021年2期
Analysis in Theory and Applications2021年2期
- Analysis in Theory and Applications的其它文章
- Deformation Argument under PSP Condition and Applications
- Diffusion with a Discontinuous Potential: a Non-Linear Semigroup Approach
- Index Iteration Theory for Brake Orbit Type Solutions and Applications
- Ground States to the Generalized Nonlinear Schrdinger Equations with Bernstein Symbols
- Classification of Positive Ground State Solutions with Different Morse Indices for Nonlinear N-Coupled Schr¨odinger System
- Ground States to the Generalized Nonlinear Schr¨odinger Equations with Bernstein Symbols
