Differentiable programming and density matrix based Hartree–Fock method?
Hong-Bin Ren(任宏斌) Lei Wang(王磊) and Xi Dai(戴希)
1Beijing National Laboratory for Condensed Matter Physics and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
3Songshan Lake Materials Laboratory,Dongguan 523808,China
4Department of Physics,Hong Kong University of Science and Technology,Clear Water Bay,Kowloon 999077,Hong Kong,China
Keywords: differentiable programming,quantum chemistry
1. Introduction
Hartree–Fock (HF) method[1]is one of the fundamental methods in many body physics. It has been widely applied in quantum chemistry to explore the ground state properties of molecules. Due to its simplicity, it is also considered as a good starting point for more accurate and expensive configuration interaction or perturbative calculations. In physics perspective, HF is a variational method whose variational space is determined by basis functions used to represent the molecular orbital. And we can achieve desired accuracy by including sufficient amount of basis functions. However,traditional HF method hasO(K4) (Kis the number of basis functions used to expand the molecular orbital) computational complexity,which suggests that calculation on large basis set is only manageable for molecules in restricted scale. Instead of monotonically increasing the amount of basis functions in basis set,researchers indicate that one could also augments the variational space of HF by treating basis function related parameters,such as exponents, contraction coefficents and centers of Gaussian type orbital (GTO),[2]as variational parameters, and updating their values during HF’s self consistent field (SCF).[3–7]Following this idea,Tachikawaet al.implemented fully variational HF method.[7]Their numerical results show that the augmented variational space can improve the total energy estimation with a small number of basis functions.
In previously reported works, gradients of total energy with respect to basis set parameters are manually derived for particular basis set and for specific molecule.This prevents the generalization of fully variational approach to practical situations. With the advent of the modern algorithm and computer technology, especially the boom of deep learning,[8]the process of manual derivation of the gradients could be replaced by automatic differentiation (AD).[9]Popular AD frameworks include Pytorch, TensorFlow[10]in Python, and ForwardDiff.jl,[11]Zygote.jl[12]in Julia.By using the state-ofthe-art AD tools,Tamayo-Mendozaet al.[13]have successfully implemented the DiffiQult library. In DiffiQult,derivatives of HF energy with respect to GTO parameters can be obtained directly from AD,which greatly simplifies the heavy derivative evaluation process, and makes it possible to efficiently compare the effects of different basis sets.However,DiffiQult uses forward-mode AD,which is not efficient for taking derivative of a function whose input dimension is larger than the output (here, the output is energy, which is a scalar). Moreover,because the number of SCF cyclies needed for converged HF calculation is undetermined before calculation starts,their gradient evaluation may cost a large amount of computation resources.
In this paper, we design a mixed mode AD method and use it to implement fully variational density matrix HF(DMHF)method proposed by Helgakeret al.[14]and Hoai.[15]Unlike the original DMHF which uses purification method[16]to guarantee the validity of one body density matrix, we use Thouless theorem[17]to directly represent the one body density matrix in a set of non-redundant parameters. In this way,we eliminate the need to perform fixed point iterations separately,and can update the density matrix and GTO parameters simultaneously in a single optimization step. Our paper is organized as follows. In Section 2, we introduce a theoretical description of DMHF method. In Section 3, we show results obtained from ground state calculation of some representative molecules, and compare the performance of our algorithm to previously published ones. At last, in Section 4, we present the conclusion and future perspective.
2. Method
2.1. Thouless theorem and parametrization of one body density matrix
The one body density matrixρis defined as

whereMjiis unconstrained and is an element of a(D?N)×NmatrixM(Dis the dimension of Hilbert space of the single particle wave function associated with those fermion operators). One could construct a Slater determinant|Φb〉which is equivalent to|Φ〉up to a normalization factor.
Therefore, by substituting|Φ〉with|Φb〉in Eq. (1), we obtain
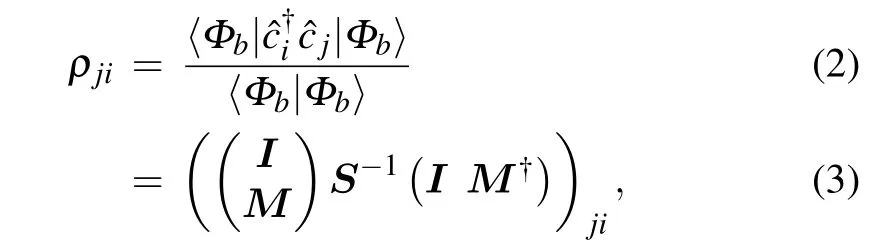
whereS=I+M?Mis aN×Noverlap matrix between single particle wave functionsφbi(x) generated by?i, i ∈[1,N].Detailed derivation can be found in Appendix A.
2.2. Variational density matrix based Hartree–Fock method
In this paper, we focus on restricted HF (RHF) method,where the molecule is a closed-shell system with all orbitals doubly occupied. In this case, the one body density matrixρis spin independent, therefore, we could omit the spin label,and write the total energy of a molecule as

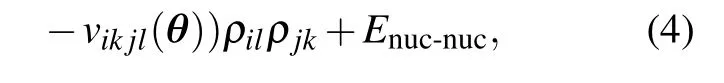
whereθis the collection of parameters of GTOs,tijis the sum of matrix element of kinetic and external potential operators under GTO,andvil jkis the tensor element of electron–electron interaction operator under GTO,andEnuc-nucis the nuclear repulsion energy inside the molecule.
From the above discussion,ρcan be parametrized byM.Therefore,by variationally optimizing Eq.(4)with respect toMandθ
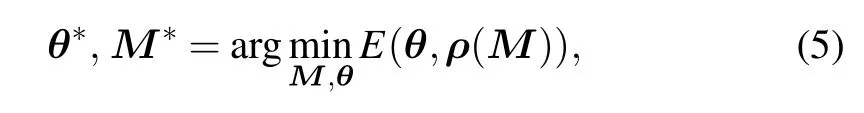
one could obtain GTOs and one body density matrix that are suitable for describing the ground state of a given molecule.
We implemented our DMHF method in Julia with AD supported by Zygote.jl. Our computation graph is demonstrated in Fig. 1. As pointed out by Tamayo-Mendozaet al.,for most of the methods in quantum chemistry,one center integral matrixtand two-center integral tensorvare constructed by an element-wise array assignment, which is not feasible for reverse mode AD to manage. We solve this problem by wrapping the array assignment operation as a primitive function that mapsθtotandv. We define custom adjoint for this primitive that computes Jacobian matrix using forward mode AD inside,then pass the Jacobian to reverse mode AD to compute the vector-Jacobian product.And because we directly parameterize the density matrix, our calculation of energy only involves matrix multiplication,trace,and tensor contraction.
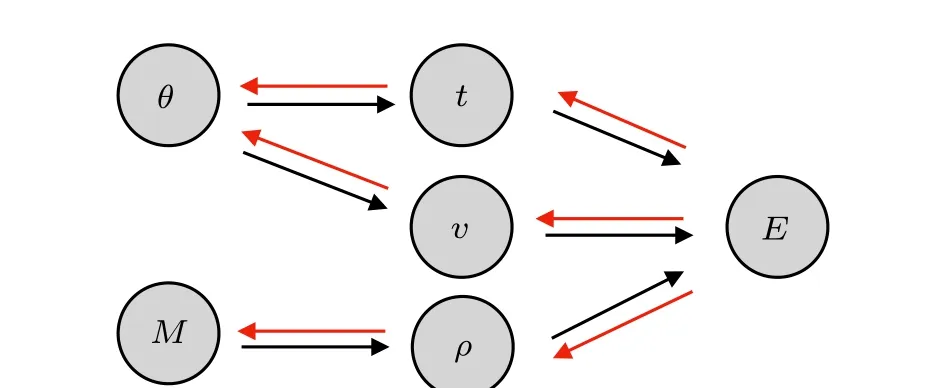
Fig. 1. The computation graph for our DMHF method. Black arrows indicate the forward function evaluation from inputs to outputs,and red arrows indicate backward steps for derivative propogation.
We demonstrate our method by the calculation of several small molecules. As a benchmark,we first perform fully variational (FV) calculation on hydrogen molecule, and compare our result to that obtained by DiffiQult. By FV,we can simultaneously optimize GTO parameters and the one body density matrix. The H–H bond length is set to 1.388 Bohr radius during the calculation. Figure 2(a)shows the variation of the ground state energy in the optimization process. We can see that our method converges much faster than DiffiQult,and could reaches a ground state energy comparable to that computed by 6-31G basis set which is two times larger than STO-3G basis we used in this case. If we switch off the variation of GTO centers,the ground state energy obtained by our method will be the same as that by DiffiQult,but still has a faster convergence rate. Figure 2(b) shows the change of ground state electron density during the optimization process. The initial electron density is calculated from a randomly initialized density matrix. After optimization, the electron density becomes reasonable and approaches the one calculated by SCF method in Ref.[18]using STO-3G basis. Since we allow the variation of GTO centers,we also find that two peaks get close to each other suggesting that FV method could partly address the polarization of molecular orbital even with a minimal basis set.

Fig. 2. Fully variational calculation of ground state of hydrogen molecule. (a) Optimization of ground state energy. The green line is calculated by FV DMHF with STO-3G basis set,the blue line is obtained using Tamayo-Mendoza et al. DiffiQult package,the dashed red line corresponds to SCF calculation using 6-31G basis set. (b)Electron density variation during the DMHF calculation,blue line corresponds to the initial electron density of hydrogen molecule before optimization,the green line is the final electron density after optimization,the dashed red line shows the SCF result with STO-3G basis. (c)Electron density distribution in the yz plane obtained from DMHF calculation,same result calculated from SCF with STO-3G is shown in dashed red line.

Fig.3. Ground state calculation of water(SCF calculation is done with PySCF).(a)Optimization process. The blue line is the result obtained by using non variational DMHF in which basis set parameters are fixed,the green line corresponds to fully variational DMHF where we optimize the basis set parameters together with density matrix, both of them are calculated use STO-3G basis set. We compare our results with those obtained from SCF calculation with STO-3G basis set (dashed orange line) and 3-21G basis set (dashed red line). (b) Difference between electron density calculated by SCF method with STO-3G basis set and 3-21G basis set. (c)Differences between electron density calculated by FV DMHF with STO-3G and SCF with 3-21G basis set.
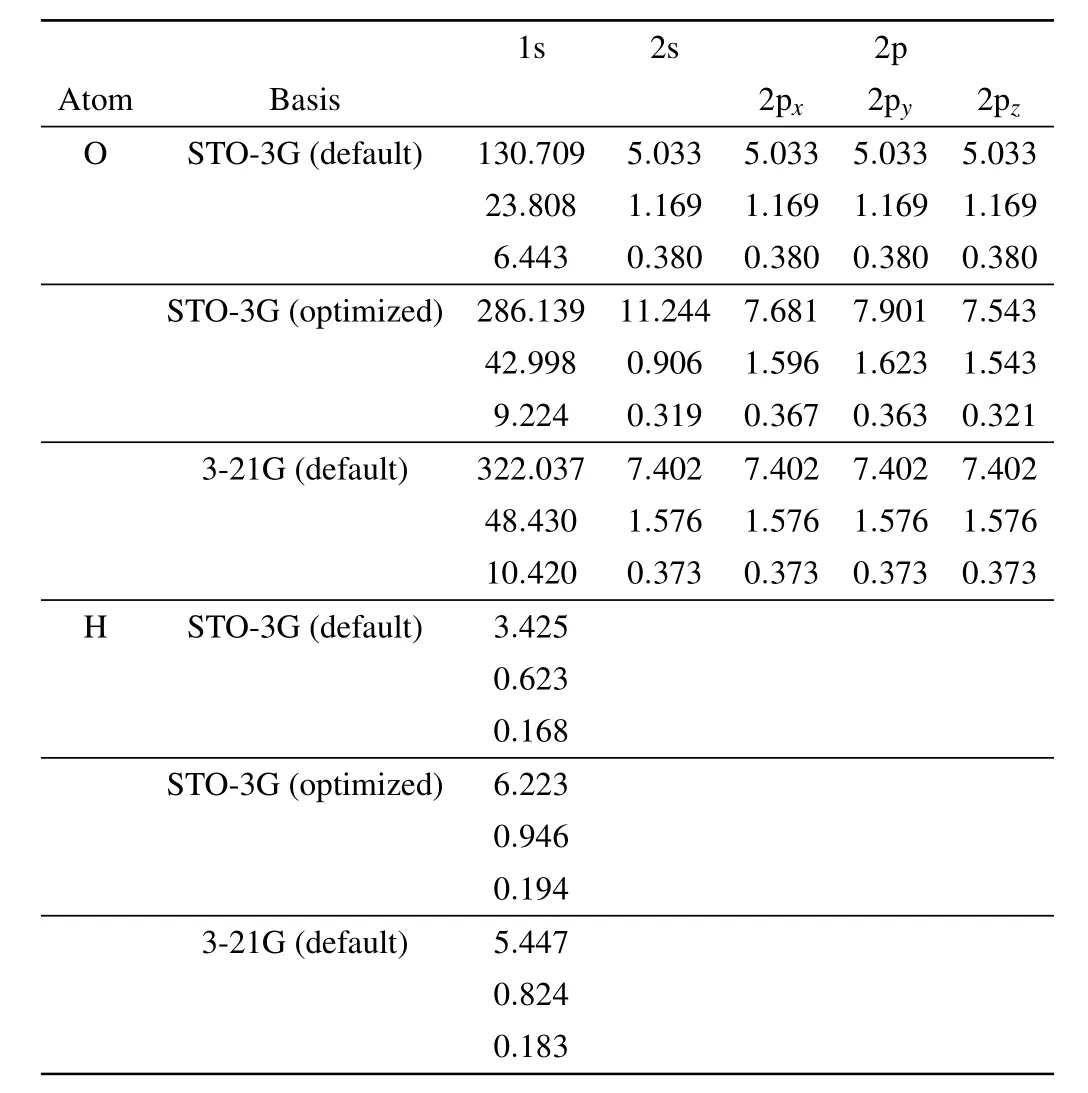
Table 1. GTO exponents of hydrogen and oxygen atoms in water, we compare the value in default setting of STO-3G and optimized STO-3G basis set to those in 3-21G basis set.
We next apply DMHF method to determine the ground state of water molecule. Fully variational calculation of water using STO-3G basis requires simultaneously optimizing 73 parameters at different scales, compared to only 13 parameters in hydrogen molecule case. In Fig.3(a),we compare the ground state energy calculated by FV DMHF and DMHF with GTO related parameters being fixed (non-variational (NV)DMHF). After optimization, NV DMHF converges to the ground state energy obtained by SCF method in PySCF,which is what we expect, while FV DMHF converges to a lower ground state energy that approximates the result obtained by SCF with 3-21G basis. Since 3-21G basis is a double zeta basis, its result is expected to be more accurate. In Fig. 4,we illustrate the variation of GTO exponents during the optimization process. We observe that starting from the default values of STO-3G basis set,these exponents finally evolve to values that are close to the default exponents of 3-21G basis set. The above results suggest that our fully variational approach makes better use of limited basis set and could effectively learn information encoded in higher dimensional Hilbert space. We also list the default and optimized GTO exponents explicitly in Table 1. In addition, in most of the commonly used basis sets, usually the same GTO exponents are applied to 2s and 2p orbitals, while in FV method, these parameters can be tuned independently which allows much larger variational space.Ground state electron density calculated from FV method is also compared to that obtained by SCF method under 3-21G basis,and the difference between the two is shown in Fig. 3(c). Compared to the electron density calculated by the default STO-3G basis set (the difference between results of STO-3G and 3-21G basis set is shown in Fig. 3(b)), our method does not force electron to be on top of each atom,allows the electron density to adjust its spatial extent appropriate to each molecular.
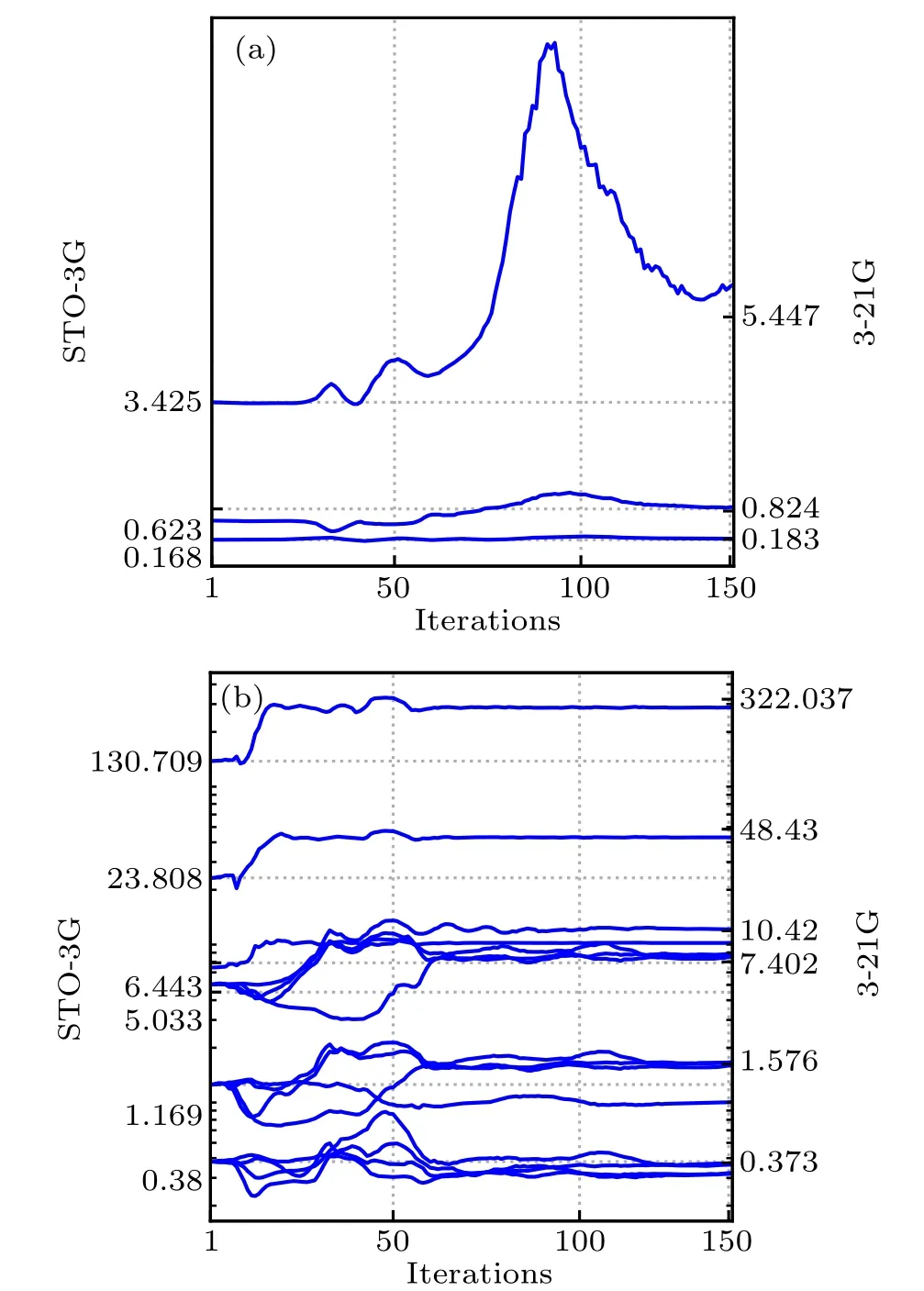
Fig.4. Evolution of GTO exponents of hydrogen(a)and oxygen(b)in water molecule during the FV DMHF optimization process. The initial value is set to the default value of STO-3G basis set,our FV approach finally sends them to a value close to the default value of 3-21G,which performs better than original STO-3G basis in computing ground state energy and electron density. These values are also listed in Table 1.
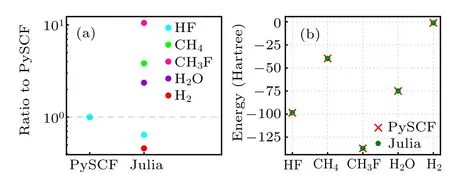
Fig. 5. Benchmark of our DMHF program with popular PySCF on several small molecules. (a)Walltime comparison between optimization process of our Julia code and SCF iterations of PySCF.The PySCF time is normalized to one, and Julia time is presented as its ratio to PySCF time. The results were obtained on single thread Intel(R)Xeon(R)E5-1650 v2 3.50GHz CPU with 16GB RAM, running macOS. (b) Comparison of the ground state energy obtained by PySCF and our Julia DMHF method.
We benchmark the performance of our DMHF implementation in non-variational setting against popular PySCF software on several small molecules,and show the benchmark results in Fig.5. We perform calculation of ground state energy of H2,HF,H2O,CH4,and CH3F on Intel(R)Xeon(R)E5-1650 v2 3.50 GHz CPU with 16GB RAM machine,running macOS,and record the time needed for converged SCF in PySCF and optimization in our Julia DMHF.We normalize the time used by PySCF calculations to 1,and show ratio of our implementation over PySCF time in Fig. 5(a). For calculation of H2and HF,our implementation surpasses PySCF,and is slightly slower than PySCF in H2O and CH4calculation. The worst case happens for CH3F,where our implementation is 10 times slower. Comparing to PySCF which derives the initial density matrix from atomic orbitals, our density matrix is randomly initialized,therefore,may require more optimization steps.
3. Conclusion and perspective
In this work,we show that one body density matrix within HF approximation can be constructed using Thouless theorem, based on which a DMHF method can be implemented.Using density matrix directly in HF helps us to remove the usual SCF that contains diagonalization of a Hamiltonian matrix in energy calculation,and enables us to use reverse mode AD for efficient gradient evaluation. When applied to calculate the ground state of small molecules, with default setting, our DMHF could achieve the same performance as traditional SCF base HF.If we allow GTO related parameters to vary, FV DMHF can be used to obtain more accurate ground state energy with a smaller basis set, which suggests the information hidden in high dimensional Hilbert space could be successfully learned by the FV approach. In future, we tend to bring the density matrix treatment to density functional theory (DFT),[19,20]which is much widely applied in the computational physics. Since we are able to extract real space electron density from density matrix, we could just replace the HF’s exchange energy calculation with the existing exchange–correlation functionals. By that, we could avoid solving Kohn–Sham equation,like what is done in orbital free DFT.
Acknowledgment
H.R.thanks Jinguo Liu for helpful discussion.
Appendix A:Proof of Thouless theorem
Consider theN-body Slater determinant|Ψ〉generated by fermion operator?1,...,?N,Thouless theorem states that
Theorem AnyN-body Slater determinant|Φ〉which is not orthogonal to|Ψ〉can be written in the form
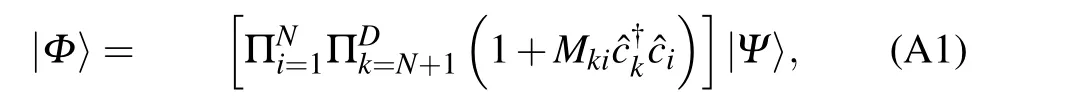
whereDis the dimension of the Hilbert space of one particle wavefunction associated with?i,andMkiare coefficients that could be uniquely determined.
To prove this, we introduce another set of fermion operator?i,the single particle wavefunctions generated by?iare in the same Hilbert space as those generated by?i. These two sets of fermion operators can be connected by a unitary transformationU
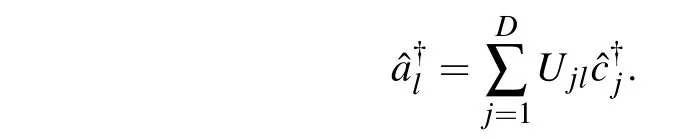
We partitionUinto four blocks:
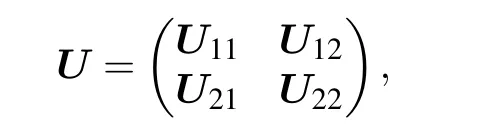
in whichU11is aN×Nmatrix,U21is(D?N)×Nmatrix.
If theNbody Slater determinant|Φ〉and|Ψ〉generated by these fermion operators
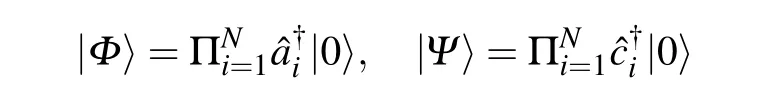
are not orthogonal〈Φ|Ψ〉/=0.We can scale|Φ〉by the inverse of〈Φ|Ψ〉

Equation(A2)is equivalent to Eq.(A1)since
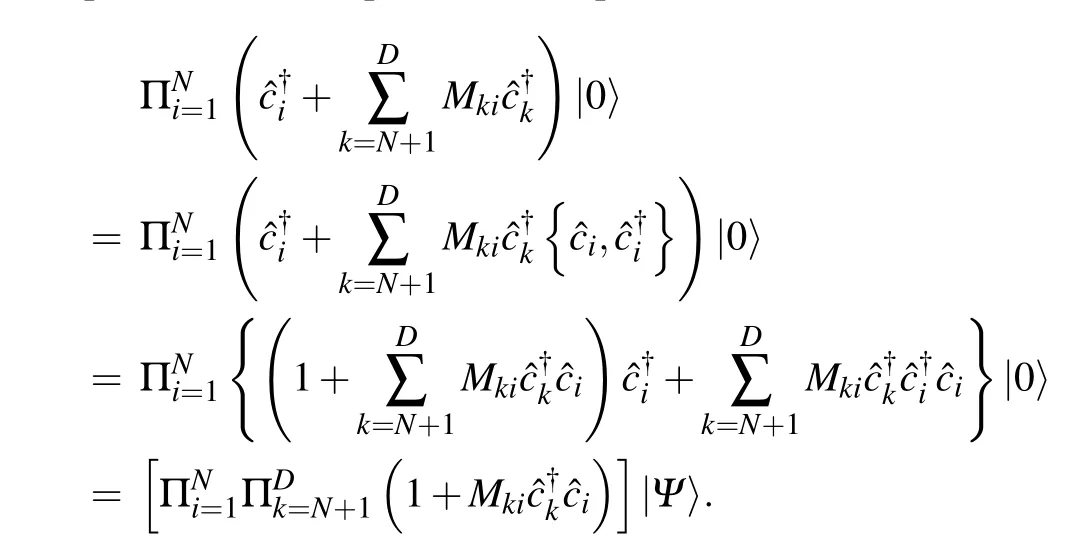
So,this proves the density matrix parameterization mentioned in Section 2.
Appendix B: Detailed proof of density matrix representation
Following notation in Section 2,the Laplace expansion of the determinant ofN×NmatrixSis known as


which suggests that
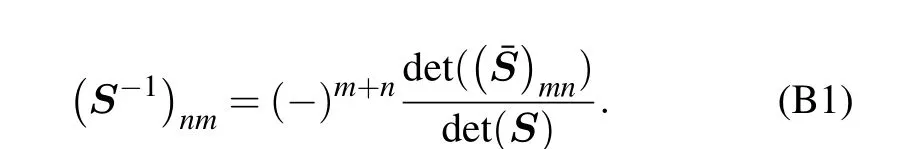
Expanding Eq.(2)and pluging in Eq.(B1),we obtain
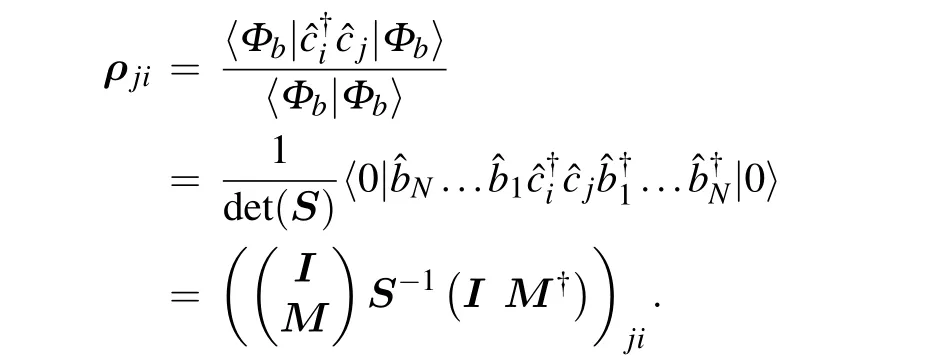

which suggests thatρis also an idempotent matrix.
The electron number conservation can be proved with the help of cyclic property of matrix trace
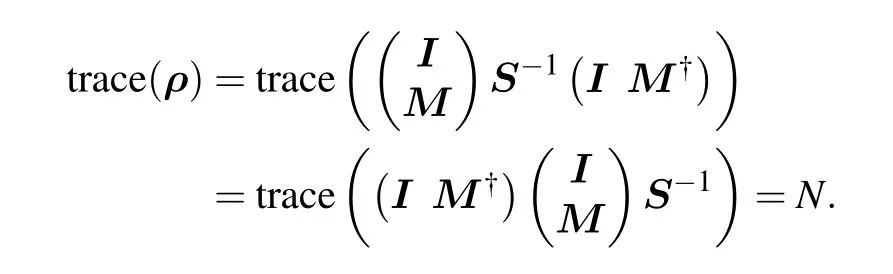
- Chinese Physics B的其它文章
- Coarse-grained simulations on interactions between spectrins and phase-separated lipid bilayers?
- Constraints on the kinetic energy of type-Ic supernova explosion from young PSR J1906+0746 in a double neutron star candidate?
- Computational model investigating the effect of magnetic field on neural–astrocyte microcircuit?
- Gas sensor using gold doped copper oxide nanostructured thin films as modified cladding fiber
- Exact explicit solitary wave and periodic wave solutions and their dynamical behaviors for the Schamel–Korteweg–de Vries equation?
- Suppression of ferroresonance using passive memristor emulator

