Statistical potentials for 3D structure evaluation:From proteins to RNAs?

Ya-Lan Tan(譚雅嵐), Chen-Jie Feng(封晨潔), Xunxun Wang(王勛勛),Wenbing Zhang(張文炳), and Zhi-Jie Tan(譚志杰)

Department of Physics and Key Laboratory of Artificial Micro&Nano-structures of Education,School of Physics and Technology,Wuhan University,Wuhan 430072,China

Keywords: statistical potential,3-dimensional structure evaluation,RNA,protein

1. Introduction

It is widely known that RNAs can pass the genetic information from DNAs to control the synthesis of proteins and can also serve as the storage of genetic information.[1]Beyond the sequence-level functions, a variety of non-coding RNAs have been discovered in recent three decades, which have extensively biological functions such as catalysis and genetic regulation.[2,3]The functions of noncoding RNAs are generally coupled to their structures or proper structure change. For example,ribozymes can only perform the catalysis of splicing or cleavage when they fold into their native 3-dimensional(3D)structures,[4]and riboswitches can only regulate the genetic expression at translation or transcription level through proper change of their 3D structures upon metabolite binding.[5]Therefore, understanding RNA structures, especially RNA 3D structures, would be critical to understanding their biological functions. Experimental methods have been widely employed to derive RNA 3D structures, such as x-ray crystallography, NMR spectroscopy, and cryo-electron.[6,7]However,until now,RNA 3D structures deposited in the protein data bank(PDB)database[8]are still limited,partially because the experimental methods are generally time-consuming and of high cost. In parallel, various computational models have been developed to predict RNA 3D structures in silico recently,[9–12]including knowledge-based and physics-based models.[13–36]Generally,a predictive model would predict an ensemble of structure candidates, and thus, a reliable scoring function becomes highly required to evaluate the quality of the candidate structures. Furthermore,a reliable scoring function can also be employed to guide RNA structure prediction and to optimize predicted structures.[37,38]

For proteins,statistical potentials,also called knowledgebased potentials or mean force potentials, have been proven to be an effective and efficient scoring function for structure evaluation in protein and protein-complex 3D structure predictions, along with the protein folding problem from three decades ago.[39–48]In the recent decade,several statistical potentials have been developed for RNA structure evaluation or prediction,[49–56]most of which were built in similar ways to those for proteins due to the prior progress made for proteins and some similar polymer features between proteins and RNAs such as backbone and side chain. Nevertheless, there is inherent difference between proteins and RNAs, such as residue types and driving forces for structure folding. Therefore,to build high-performance statistical potentials for RNAs may still require the involvement of the structure characteristics of RNAs,in addition to utilizing similar modeling experience for proteins.

In this review, we will firstly introduce the derivation of general formulas for statistical potentials based on fundamental principles. Afterwards, we will give a brief overview on typical traditional statistical potentials for protein 3D structure prediction and evaluation due to the important reference role for RNAs. After that, we will introduce the recent advances in the statistical potentials for RNA 3D structure evaluation.Finally,we will emphasize a perspective on the further development of new statistical potentials with higher performance for RNA 3D structure evaluation.

2. Fundamental principles for statistical potentials

There are two fundamental principles for deriving and utilizing a statistical potential for proteins or RNAs: (i) the probability of a conformation of a biomacromolecule in a conformation ensemble obeys the Boltzmann’s law which connects the effective potential energy of the system to its probability;[39,57,58](ii) the native structure of a biomacromolecule corresponds to the conformation with the lowest free energy,which was first demonstrated by Anfinsen in 1973[59]and connects the free energy minimum of a biomacromolecule to its native structure.[58]

In addition, a native folded structure is actually driven and stabilized by various complex intramolecular and intermolecular interactions, while there would not exist a perfect potential energy function to exactly describe all these interactions for a biomacromolecule system.[58]Practically, a biomacromolecule system can be considered as an equilibrium ensemble of different atom(atom block)pair types with different types of characterizing geometrical parameters such as inter-atom contact, inter-atom distance, inter-atom angle,inter-block orientation,and so on. If a geometrical parameter is chosen,the probability of describing different values of the geometrical parameter can be utilized to build a statistical potential as a function of the geometrical parameter for different atom(or atom block)pair types.

2.1. Derivation of statistical potential

In principle,any kind of geometrical parameters,such as distances or angles between atoms which can be utilized to distinguish a native conformation from decoy ones, can be adopted to derive a statistical potential.[48]According to the inverse of Boltzmann’s law, the potential energy for a particular atom pair type in the native state ensemble of biomacromolecules can be expressed by[40]

where kBand T are the Boltzmann constant and the temperature in Kelvin, respectively. Eobs(s) and Pobs(s) are the energy and observed probability of a particular atom pair type for a geometrical parameter s in the native structure ensemble.Zobsis the summation of Boltzmann factor over geometrical parameter s in the native state ensemble

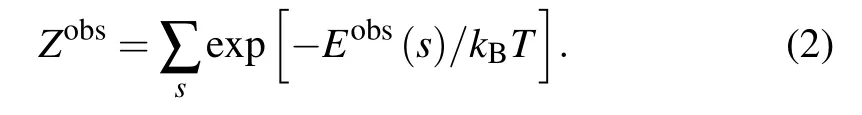
However,Eobs(s)includes not only the interactions we focus on but also other interactions from surrounding medium.[60]Therefore, to obtain an effective statistical potential ?E(s), a reference state needs to be involved. Similarly, according to Eq. (1), the inverse of Boltzmann’s law for a reference state can be written as[40]

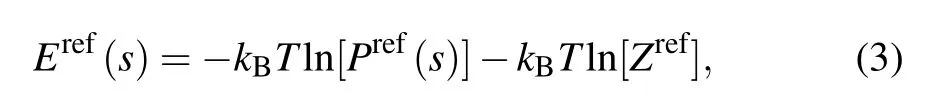
where Eref(s) and Pref(s) are the potential energy and the probability of the geometrical parameter s in a reference state,and Zrefis the summation of Boltzmann factor over geometrical parameter s in the reference state ensemble

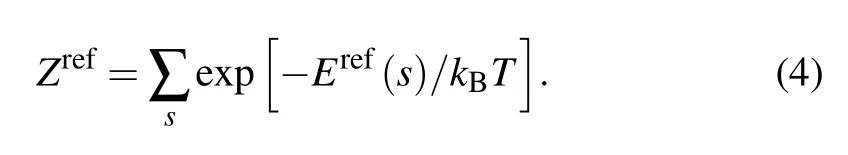
Therefore, a net statistical potential is obtained as a function of geometrical parameter s[40]

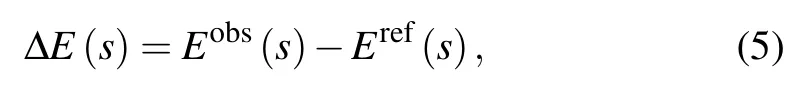
and from Eqs. (1) and (3), ?E(s) can be computed from the probability Pobs(s)and Pref(s)by

In addition, at a fixed temperature, Zobs/Zrefis a constant and independent of the geometrical parameter s for a given amino/nucleic acid sequence,[40]and consequently?kBTln[Zobs/Zref] can be treated as zero point of the potential. Therefore, a general expression of a statistical potential can be obtained as[40]

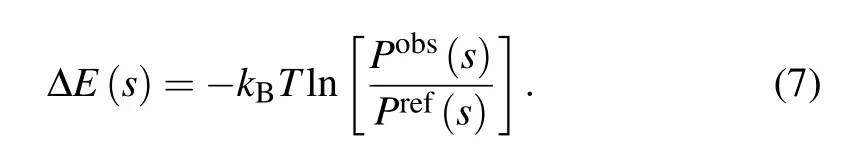
As shown in Eq.(7),the geometrical parameters s,which may involve two or more atoms (or atom group) and the reference states,are crucial for building statistical potentials,and the core difference between various statistical potentials is attributed to their choice.

2.2. Utilization of statistical potential

After deriving a statistical potential from Eqs. (1)–(7),the total energy ?E(S,C)for a conformation C of a given sequence S relatively to the reference state can be given by[40]

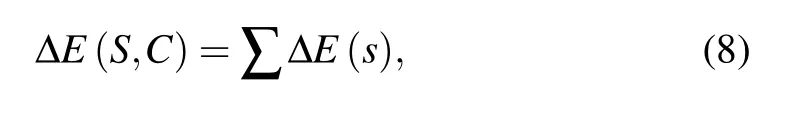
where the summation is over all atom(atom block)pairs with the additive assumption for statistical potentials.[40]

3. Statistical potentials for protein 3D structures

Since the pioneering work of Tanaka and Scheraga in 1976,[39]various strategies have been proposed to develop effective statistical potentials for proteins at atom or residue level.[40,42,43,61–64]These strategies can be roughly classified into the following categories: (i)developing various reference states or circumvent reference states;[43,65–70](ii) classifying short-, medium-, and long-range interactions;[39,57,72–74](iii)considering different geometrical parameters such as multibody[63,75–79]and orientation-dependent interactions.[80–86]The geometrical parameters and major features of existing approaches employed in developing statistical potentials for proteins have been summarized in Table 1.

Table 1. The mainly existing approaches in developing statistical potentials for proteins.

3.1. Existing widely used reference states

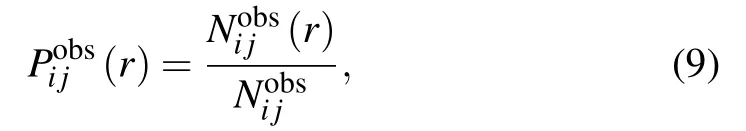
The existing reference states can be roughly classified into two types: based on experimental structures in PDB database[43,65,68]and based on statistical physics models.[66,67,69]The former type includes averaging reference state,quasi-chemical approximation reference state,and atomshuffled reference state, and the latter type includes finiteideal-gas reference state, spherical-non-interacting reference state,and random-walk-chain reference state.

3.1.1. On the basis of experimental structure database

where Nobs(r)is the number of atom pairs within distance interval of [r,r+dr] from experimental structures in database,and Nobsis the summation of Nobs(r) over all distance intervals.

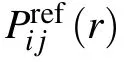
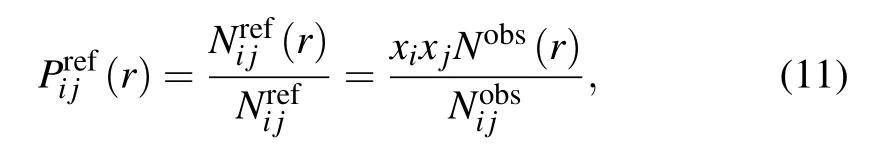
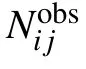
3.3. Classification of short-, medium-, and long-range interactions

Tanaka and Scheraga have classified the inter-residue interactions into short-, medium-, and long-ranged ones for proteins,[39]and the criteria for interaction ranges of proteins are based on the separations between residues along protein sequences. Afterwards,the preference of amino acids to form short-, medium-, and long-range contacts has been analyzed for different types of proteins,[72–74,89]and several potentials have also been proposed based on distinguishing interaction ranges.[57,72,91–94]The classification of interaction ranges may be very necessary since such treatment can involve more accurate information extracted from native structure database in different interaction ranges.

3.3.1. Backbone torsion-based potentials

To measure the influence of amino acids on the backbone conformation of neighboring residues along protein sequences, backbone torsion-dependent potentials were proposed by Rooman et al.[91]and Kocher et al.[92]A succession of dihedral angles φ, ψ, and ω of each residue represent the backbone of proteins, and these dihedral angles can be clustered into 7 domains.[91]Based on Eqs. (7) and (8), the total torsional energy for a protein conformation can be expressed as the summation of residue-to-torsion potentials along the protein conformation[92]

3.4. Extraction of multi-body interactions

Beyond widely used pairwise two-body potentials,multi-body potentials, especially for three- and fourbody potentials, have been proposed for capturing higherorder interactions.[63,75–79,95–97]In addition, several geometrical techniques, such as Voronoi diagram, Delaunay triangulation,[98]and alpha shape[76,96]were employed to define the neighboring bodies and to identify the multi-body interactions.

3.4.1. Three-body potentials

Three-body contacts have been introduced in several studies where physical models were developed with explicitly incorporating a three-body interaction.[95,96,99–101]Based on Delaunay triangulation, Li and Liang used the alpha shape to define three-body interactions for protein structures.[96]Here,we briefly introduce this approach as an example of this class of statistical potential. In the model of Li and Liang, volume overlap was used to identify three-body contacts, and such volume overlap occurs if three atoms from nonbonded residues share a Voronoi vertex.[96]Furthermore,Li and Liang introduced a nonadditive coefficient by measuring the deviation of three-body interactions from three independent pairwise interactions.[96]The nonadditive coefficient v of threebody interactions was defined as[96]

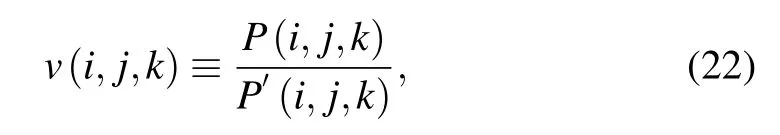
where P(i,j,k) is the three-body propensity for residues of types i, j, and k in native structure database, and P′(i,j,k)is the propensity if the three-body interaction is the simple consequence of three independent pairwise contact interactions. The expressions of P(i,j,k) and P′(i,j,k) are written as follows:[96]

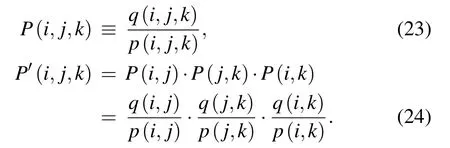
Here, P(i,j) is the pairwise contact propensity for residue types i and j, and P(i,j) equals to the odds ratio of the observed probability q(i,j) for two-body contact of residues i and j to the excepting probability p(i,j)for two-body contact of residues i and j. The observed probability q(i,j,k)and expecting p(i,j,k)are for three-body contact,respectively. The details of calculating p(i,j), q(i,j), q(i,j,k), and q(i,j,k)can be found in Ref.[96].Finally,the potential energy ?E(M)for a molecule M modeled as a set of fused hard spheres can be expressed as[96]

where σij∈κ represents pairwise alpha contacts,and σijk∈κ represents three-body alpha contacts.

3.4.2. Four-body potentials

To capture more complicated interactions, several fourbody potentials have been developed,[63,75,77–79,95,97]and Delaunay tessellation algorithms were widely used for finding the nearest neighbors in native structures. Krishnamoorthy and Tropsha have verified that their four-body potentials derived with Delaunay tessellation performed better than pairwise two-body potentials in distinguishing correct sequences/structures and generating Z-scores.[77]Later,considering more detailed interactions between backbones and side chains and including some of the sequential information of proteins,Feng et al. have proposed a new four-body statistical potential based on Delaunay tessellation.[78]Instead of using Delaunay tessellation, Gniewek et al. have used a simple geometric construction to develop a four-body contact potential,and they found that the performance of their optimized coarsegrained contact potentials was comparable to the performance of DFIRE for all proteins larger than 80 amino acids.[79]

As shown above, due to the huge computational complexity and limited structure data, most existing multi-body potentials are based on local residue contact rather than distance and with the growth of protein structures deposited in database, multi-body distance-dependent statistical potentials can be developed for capturing higher order interactions in protein structures.

3.5. Involvement of orientation-dependent interaction

Atoms in proteins generally carry charges and thereby there can exist orientation-dependent correlations between polar atom blocks due to dipole–dipole-like interaction and associated polarization effect.[85]Consequently, orientationdependent correlation between atom blocks has been considered as a complementary contribution to above described statistical potentials. Recently, Wang and Huang have shown that the involvement of orientation contribution can visibly improve the performance of the statistical potential.[86]In geometry, the relative position and orientation between two 3D objects need to be determined by six degrees of freedom, including three translations and three rotations, or one distance and five angular variables.[83]Hence,the definition and calculation approaches for the orientation between two blocks are more diverse than those for the distance of two blocks, and a more adequate native structure database is needed for developing orientation-dependent statistical potentials.

3.5.1. Definition of relative orientation

Ideally,for proteins,an amino acids residue can be represented by several blocks,and each block is centered by each of heavy atoms. As shown in Fig.1(a),the relative orientation of a block pair is described by five angles: θi,?i,θj,?j,and ωij.The first four angles are the polar coordinates of the rijvector in the local 3D reference frame of each amino acid and ωijdescribes the relative rotation of Vzvectors of two amino acids along the rijaxis. The local 3D reference frame is defined as

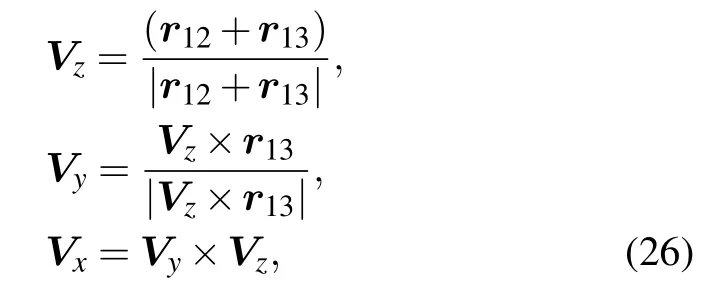
where r12=r(i1)?r(i)and r13=r(i2)?r(i)are the relative vectors from atom i to atoms i1and i2,respectively;Vzis the normal vector to the plane within which Vxand Vzlie.

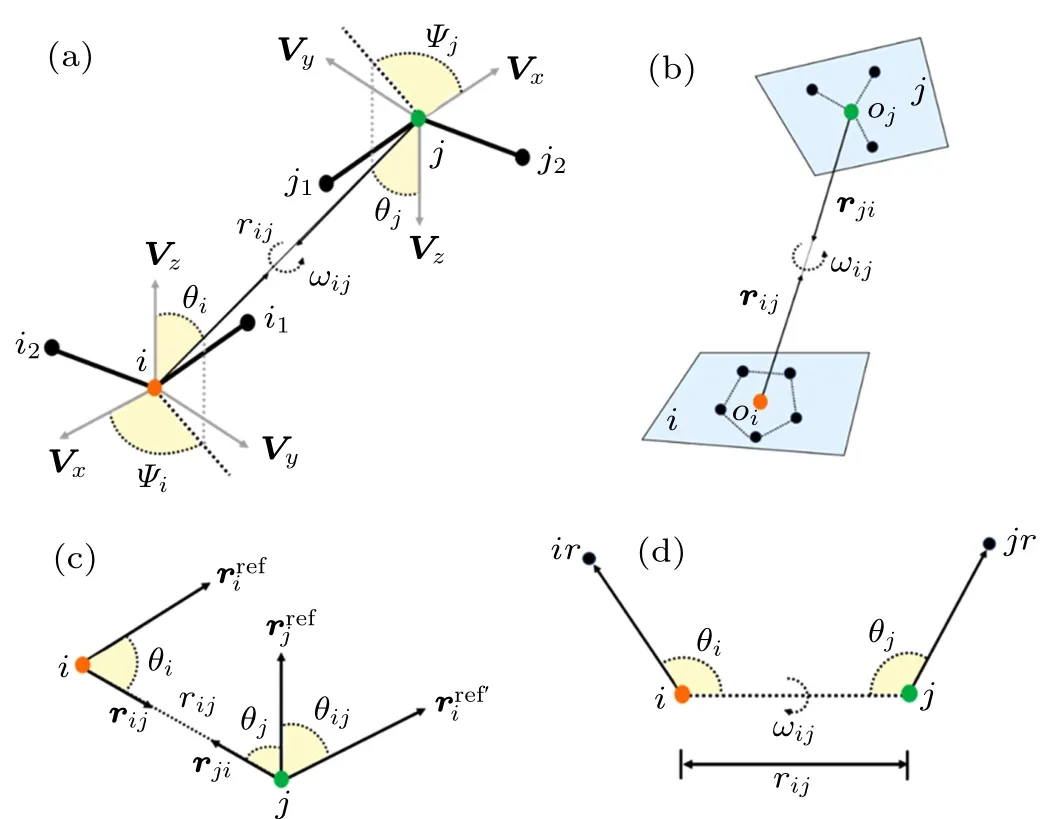
Fig.1. (a)The complete definition of relative position and orientation between two blocks centered by atoms i and j, respectively, in which one scalar distance rij and five scalar angles(θi,Ψi,θj,Ψj,ωij)parameters are used. (b) The definition of relative position and orientation between two blocks i and j for OPUS-PSP,in which two direction vectors ri j and rji and one scalar inter-rotation angle ωij parameters are used. (c) The definition of relative position and orientation between two polar atoms i and j for dDFIRE, in which one scalar distance rij and three scalar angles(θi,θj,θi j)parameters are used. (d)The definition of relative position and orientation between two atoms i and j for ORDER_AVE,in which one scalar distance rij and three scalar angles(θi,θi,ωij)parameters are used.

Afterwards,by taking the relative position and orientation as geometrical parameters,equation(7)can be rewritten as

3.5.2. Recent developed orientation-dependent potentials

A perfect definition of relative orientation for proteins is so detailed that building an orientation-dependent potential would experience the challenge of sparse experimental data and long computational quantity. The existing strategies used to overcome the problem mainly include: (i) reducing representations of proteins; (ii) reducing variables of defining the orientation;and(iii)reducing dimensions of the joint probability distribution. In this subsection, several recent orientationdependent statistical potentials are briefly introduced as follow.

OPUS-PSPOPUS-PSP potential,proposed by Lu et al.,defines orientations for blocks of atoms bonded rigidly within the same residue.[80]In OPUS-PSP potential, 20 amino acid residues are decomposed into 19 rigid-body block types, in which all heavy atoms are assumed to be in the same plane,and each residue contains several blocks. As shown in Fig.1(b),the relative orientation of blocks i and j respectively with the origins oiand ojis determined by two relative direction vectors rijand rji, and an inter-rotation angle ωij. For the differences among these 19 rigid-body blocks, the definition of local 3D reference frame for each block type and interrotation angle is specified,which can be found in Lu et al.[80]Finally, the orientation-dependent energy function can be expressed by[80]

In dDFIRE,the finite-ideal-gas reference state was used as the reference state.

ORDER_AVEORDERAVE is a four-dimensional joint probability distribution with five atoms per residue.[102]As shown in Fig.1(d), for atom pair i and j, two heavy atoms ir and jr that directly connect to i and j, were selected, and the orientations of atoms i and j can be described by four variables, rij, α, β, and γ. Here, rijis the distance between atoms of types i and j; α and β are the scalar angles of the atom groups ir–i–j and i–j–jr,respectively;and γ is the dihedral angle of atom groups ir–i–j–jr. Finally, the orientationdependent energy ?Eijfor the atom pair i and j can be expressed as[102]

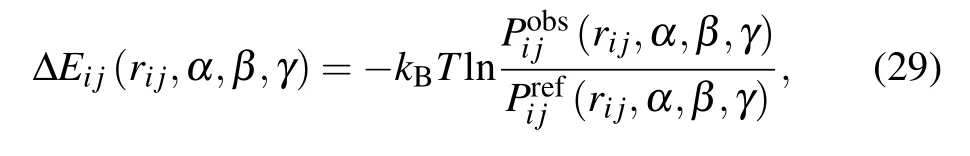
KORPKORP, a side-chain independent potential, was defined by a 6D joint probability that only depends on the relative orientation and position of three backbone atoms.[83]As shown in Fig.1(a),six parameters including a distance rijand five angles (θi,?i,θj,?j,ωij) are used. However, it is quite challenging to obtain a detailed 6D joint probability based on the relatively small number of experimental structures. Thus,a constant z was added to prevent infinite values for very small probabilities and to improve the numerical stability for lowcount statistics,and the orientation-dependent potential can be given by[83]

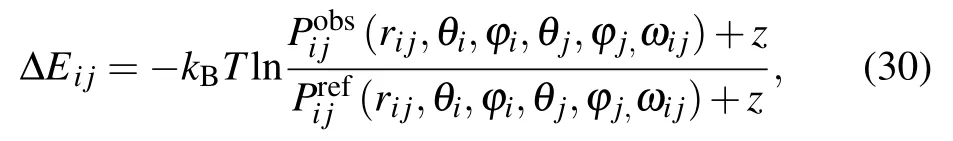
The above described involvements of orientationdependent potentials can provide a very valuable contribution to a statistical potential,[80,83,85,102]while due to sparse experimental data and long computational cost, the quality of an orientation-dependent potential may strongly rely on the definition of relative orientation for atom groups in proteins.

4. Statistical potentials for RNA 3D structures

In the recent decade,as the number of experimental RNA 3D structures deposited in PDB database[8]increases,several statistical potentials have been derived based on known structures for RNA structure prediction and assessment,[37,49–56]partially with the aid of the experience for proteins. However,the existing statistical potentials for RNAs are significantly less than those for proteins and still do not reach a satisfactory performance. In the following, we will give an overview on the recently developed statistical potentials for RNA 3D structure evaluation and will emphasize the possible development on statistical potentials for RNAs in the near future.

4.1. Existing statistical potentials for RNAs

To our knowledge, the existing statistical potentials for RNA 3D structure evaluation[50–56]were developed(partially)with the aid of the experience or those in protein structure prediction and assessment. The existing statistical potentials for RNAs have been organized in Table 2,and will be introduced explicitly in the following.

4.1.1. Distance- and torsion angle-dependent statistical potentials

RASPBased on the averaging reference state, Capriotti et al. have built RASP at both coarse-grained and all-atom(23 clustered atom types) levels from a non-redundant training set of 85 RNA structures,and distance between atom pairs was considered as the geometrical parameter.[51]Capriotti et al. have shown that RASP has a better performance than NAST[37]which is a nucleotide-level coarse-grained statistical potential composed of bond,angle,dihedral,and non-bond terms.

KB potentialUsing the quasi-chemical approximation reference state, Bernauer et al. have derived distancedependent and fully differentiable statistical potentials at both coarse-grained and all-atom (85 atom types) levels from a training set of 77 native RNAs.[50]Owing to the implementation of Dirichlet process mixture models, the statistical potentials are fully differentiable,which makes them applicable for molecular dynamics simulations.

3dRNAscoreDifferent from RASP and KB potentials, 3dRNAscore is composed of the distance- and torsion angle-dependent potentials based on the averaging reference state.[52]In 3dRNAscore, 85 atom types and 7 torsion angle types were defined, and a set of 317 RNA native structures was used for training the potential.[52]In addition, to appropriately consider the contributions of the two kinds of energy terms, a weight factor w has been optimized by four typical RNA decoys.[52]The test of 3dRNAscore has shown that, the dihedral-dependent potential alone performs visibly worse than the distance-dependent potential averagely,while the combined potential with dihedral-dependent and distance-dependent contributions generally performs better than the distance-dependent potential.[52]Thereby, the dihedral-dependent potential has been verified useful to improve the accuracy of a distance-dependent potential.

According to the results reported by Wang et al.,[52]overall,the performance of RASP is worse than that of KB potential and 3dRNAscore, and 3dRNAscore has the best performance among these three statistical potentials.[52]The mainly reasons might be that the KB potential of all-atom and 3dRNAscore are based on 85 atom types,while only 23 clustered atom types are involved in the all-atom version of RASP. In addition, the best performance of 3dRNAscore might be attributed to the explicit emphasis on the local torsional structure feature of RNA backbones which can be important for RNA 3D structures.

4.1.2. Comparisons of different reference states for RNA 3D structure evaluation

For RNAs, only the averaging and quasi-chemical approximation reference states were used to build statistical potentials until our very recent study.[55]To understand the existing widely used six reference states for RNAs, we performed a comprehensive examination on these six reference states,including the averaging,quasi-chemical approximation,atom-shuffled, finite-ideal-gas, spherical-non-interacting, and random-walk-chain reference states; see also Subsection 3.1.In the work,[55]using the same training set and parameters,e.g., bin width and distance cutoff, we constructed six allatom(85 atom types)distance-dependent statistical potentials corresponding to the six reference states,and examined these potentials against three RNA test sets;see Table 2. Our extensive examinations showed that, overall, for identifying native structures and ranking decoy structures,the finite-ideal-gas[66]and random-walk-chain[69]reference states were slightly better than others, while for identifying near-native structures,there was slight difference among the six reference states.Moreover, compared among RASP, KB potential, and 3dRNAscore,3dRNAscore has the similar performance to the top ones of these six statistical potentials, while RASP and KB potential have visibly lower performance than the others.[55]

Table 2. The existing statistical potentials for RNA structure evaluation.

4.1.3. Four-body contact potential

Masso has developed a four-body contact potential of RAMP, which is the first multibody statistical potential for RNAs.[56]In RAMP, atomic four-body nearest-neighbors were generated by the Delaunary tessellation[98]for each structure in a training set of 85 native RNAs, and each RNA was represented by four atom types of C,N,O,and P.[56]Thus,35 distinct quadruplet types can be produced by 4-letter atomic alphabet. With atomic quadruplet contacts as geometric parameter and the inversed Boltzmann’s law,equation(7)can be rewritten as[56]

4.1.4. Utilization of 3D convolutional neural network

Completely diverged from the above-described traditional statistical potentials, Li et al. have employed a 3D convolutional neural network to develop two 3DCNNbased scoring models, named RNA3DCNN_MD and RNA3DCNN_MDMC, for assessing near-native RNA decoys and RNA decoys with large root-mean-square-deviation(RMSD) fluctuation, respectively.[53]Two training sets were generated by molecular dynamics (MD) simulations and Monte Carlo (MC) structure prediction for each of 414 RNAs. RNA3DCNN_MD was trained by the frist set, while RNA3DCNN_MDMC was trained by the training set combined the two training sets. The test showed that, for decoys with RMSD less than 1.0 ?A,the performance of RNA3DCNN was similar to or worse than that of traditional statistical potentials, while for decoys generated by RNA structure predictive models, RNA3DCNN performed obviously superior to other existing statistical potentials in identifying native structures.[53]

4.2. Limitation of current statistical potentials and perspective for RNAs

According to Eq. (1), a set of pairwise potentials can be extracted from the distance distribution of atom pairs by the inverse of Boltzmann’s law. However, an individual pairwise potential involves not only the interaction between two atoms but also the influence of the surrounding medium on the interaction.[60]Therefore, reference states and other approaches have been developed aiming to eliminate redundant information.Based on the experiences in protein structure prediction and assessment from which the existing RNA statistical potentials benefit,we will make a brief discussion for developing new statistical potentials for RNA structure evaluation.

4.2.1. On reference states

The existing six reference states can be classified into two types: based on experimental RNA 3D structures[43,65,68]and based on physical modeling.[66,67,69]The physical-modelbased reference states are built by various physical models,and they can better describe the conformation space of RNA decoys than the 3D-structure-based reference states.However,the physical-model-based reference states are still deviate significantly from the ideal one due to the ignorance of detailed structure features,and our recent study shows that the performance of statistical potentials based on physical-model-based reference states is still not at a high level for realistic decoys from RNA structure prediction models.[55]For example, the ideal-gas reference state completely neglects the connectivity of RNA chains,and a random-walk reference state ignores the intrinsic rigidity of RNA chains. Moreover,both of the reference states neglect side chains and atom types. Therefore, it is still necessary to propose more realistic reference states for RNAs or circumvent the problem of reference states.

One possible way to simulate more realistic RNA chains is to involve the chain rigidity of RNAs, e.g., an RNA chain is modeled as a semiflexible polymer rather than a completely random polymer.[103,104]Another possible way is to develop a combined reference state composed of the physical-modelbased and structure-based reference states which may complement each other. A third possible way is to develop an ensemble-based reference state of ideal-gas-like states of different dimension parameters or of random-walk-chain states of difference Kuhn lengths, since backbone atoms and side chain ones may behave very differently. Due to the difficulty in modeling an ideal reference state, an alternative way is to circumvent the problem. Huang and Zou have proposed an iterative method to develop scoring functions for protein–ligand and protein–protein docking.[61,62]This method provides a possible way to circumvent reference states for modeling statistical potentials for RNAs, although the performance may rely strongly on the high-quality decoy training set which should be generated by various structure prediction models.

4.2.2. On short-,medium-,and long-range interactions

Tanaka and Scheraga[39]have classified the inter-residue interactions into short-, medium-, and long-ranged ones for proteins, and afterwards, the preference of amino acids to form medium-and long-range contacts between has been analyzed for proteins.[72–74,89]Until now,most statistical potentials for RNAs do not distinguish the contributions of short-,medium-, and long-ranged interactions. However, these different residue-separation-ranged interactions should play different roles in RNA folding process or in stabilizing folded RNA structures. For example,the short-,medium-,and longranged potentials may correspond to the interactions within loops, those stabilizing secondary segments, and those stabilizing tertiary contacts for RNAs. Although the local interactions were split from non-local interactions in RASP by Capriotti et al.,[51]the local potential was built at each nucleotide separation which is too subtle to avoid sparse data problem and might not be able to represent specific topological features. Therefore, the classification of short-, medium-, and long-ranged interactions is in accordance with the folding and structure features of RNAs and may be valuable for developing statistical potentials of higher performance for RNA structure evaluation.

4.2.3. On geometrical parameters

Compared with pairwise two-body potential, multi-body potential could capture more complex 3D interactions.[78,96]Up to now,RAMP is the only RNA four-body statistical potential,but its overall performance is not better than that of RASPALL,[56]which may be attributed to that RAMP only involves four atom types to represent RNA structures and RAMP is a (spatially) local contact potential ignoring spatially nonlocal interactions. Therefore, for building a multi-body potential, a proper geometrical parameter may be very important which should not only describe the key geometrical relation between multi-body atoms, but also be conveniently used to build a multi-body potential based on limited native structure database.Another key problem in modeling multi-body potential may be the coarse-graining of RNA atoms which should not only retain the major structure feature of RNAs, but also effectively decrease the complexity of multi-body potentials and the demand for structure data in training set.

On the other hand, most existing RNA statistical potentials are distance-dependent, expect for 3dRNAscore which is composed of the distance- and the local torsional angledependent terms.[52]The better performance of 3dRNAscore than prior traditional statistical potentials is mainly attributed to the explicit emphasis on the local torsional structure feature of RNA backbone. Hence, other geometrical parameters can be involved into distance-dependent statistical potentials to improve the performance, such as orientation, which has been highlighted important for proteins;[86]see Subsection 3.5. Another geometrical parameter can be the nonlocal torsional angle beyond one nucleotide, which may also improve the description for RNA backbone and be helpful for a distance-dependent potential. Owing to current limited experimental RNAs, it is very important to define the orientation variables,the importance of which has been discussed above.Based on current limited experimental RNAs,it is very important to define the orientation variables and deal with the dependence among the variables. Compared to 20 amino acids with 167 atoms for proteins,RNAs has 4 nucleotides with 85 atom types, which may make it easier to build high-performance orientation-dependent potentials for RNAs.

4.2.4. On unique feature of RNAs

From the above, the existing statistical potentials for RNAs were developed mainly according to those for proteins.There are some important similar structure features between RNAs and proteins. For examples, first, RNAs and proteins are both polymers with backbones and side chains. Second,there are distinctively ordered secondary segments in RNA and protein structures, such as helices and loops for RNAs,and α-helices,β-sheets,and loops for proteins;third,the tertiary structures of RNA and proteins are both very compact and approximately sphere-like. Such similarity between RNA and proteins structures has enabled the great benefit of the existing statistical potentials for RNAs from those for proteins.

However,there are also several distinctive differences between RNAs and proteins. The major forces for stabilizing structures are very different for RNAs and proteins. RNAs are generally stabilized by strong secondary interactions of base-pairing/stacking and moderate tertiary interactions,while proteins are generally stabilized by hydrophilic and hydrophobic interactions. Consequently, the secondary and tertiary interactions for RNAs may be roughly classified while those for proteins are mutually coupled. The separate involvement of secondary and tertiary contributions in a statistical potential may improve its performance. Furthermore, basestacking can promote the helical orientation of RNAs and consequently RNA structures are apparently less spherical than protein structures,[105,106]which may suggest that angular or orientation-dependent contribution is more important for a statistical potential for RNAs.

Very importantly, RNAs are strongly charged polyanion,[106–109]which is distinctively different from proteins generally with certain positively and negatively charged domains. Generally, for RNAs, metal ions are essentially required to neutralize the negative charges on RNA backbones,and consequently would favor the folding of compact native structures. Furthermore, cations with different valences and concentrations could have very different influences on the deformation of folded RNA structures.[108,109,111–113]For example, due to polyanionic nature, RNA structures can become less compact at lower salt and an RNA can have visibly more compact structure at multivalent salt than at monovalent salt.[32,33,35]Therefore,the involvement of ion-electrostatic interaction in a statistical potential may be helpful for improving its performance for RNA 3D structure evaluation, especially for the NMR structures.[55]Finally, machine and deep learning methods which could dig critical and uneasy to be detected RNA feature information are also able to be applied to build statistical potentials.[53]

5. Conclusions

Since various computational RNA 3D structure prediction models have appeared in recent years, scoring functions are essentially needed for evaluating the predicted structure candidates. Because statistical potentials for protein 3D structure prediction and evaluation have been developed from a long time ago,there are lots of experience which can be very helpful for RNAs. In this review, we firstly introduced the fundamental principles of deriving the formulas of statistical potentials. Afterwards, we gave a brief view on the development of statistical potentials for proteins, and we emphasize the choice of geometrical parameters and reference states which are crucial for building different statistical potentials.Furthermore, we introduced the recent advances in statistical potentials for RNAs. Finally, we make a detailed discussion on possible further improvements of statistical potentials for RNAs,which may be helpful for developing high-performance statistical potentials for RNA 3D structure evaluation.

Acknowledgements

We are grateful to Professors Shi-Jie Chen(University of Missouri), Xiaoqin Zou(University of Missouri), Jian Zhang(Nanjing University), Yi Xiao (Huazhong University of Science and Technology),and Sheng-You Huang(Huazhong University of Science and Technology)for valuable discussions.