Review of quantum simulation based on Rydberg many-body system

Zheng-Yuan Zhang(張正源), Dong-Sheng Ding(丁冬生), and Bao-Sen Shi(史保森)

Key Laboratory of Quantum Information,University of Science and Technology of China,Hefei 230026,China

Keywords: many-body,quantum simulation,Rydberg

1. Introduction

Simulation is an essential method for problems whose solutions are impossible or too expensive to resolve. Many-body problem is one type of them. Due to the complicated interactions,the dynamics of each member in the many-body system cannot be calculated precisely once the system consists of tens of particles, which is just a small ensemble compared to the real-world systems. Luckily, a number of many-body problems can be simplified to some specific models,and solutions to these problems may be found by studying these models.Besides theoretically solving, we can couple these models into specific physical systems and search regularities from experimental results, which is called simulation. For the quantum field problems,simulations should be conducted in a controllable quantum system, which takes the laws of quantum dynamics to calculate and evolve.That is the concept of quantum simulation initially proposed by Richard Feynman about forty years ago.[1]Until now, quantum simulation has been widely and successfully applied in physics and other fields.

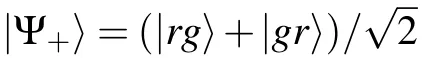
There are mainly two types of quantum simulations based on Rydberg atoms. One needs to control each atom in the many-body system in cases where atoms are always trapped in arrays, such as Ising model,[16–18]XY model,[19]and SSH model.[20,21]The other builds a driven and dissipative system corresponding to the real system and controls atoms in facilitated avalanche excitations. This kind of simulation includes non-equilibrium phase transitions and a self-organized model.

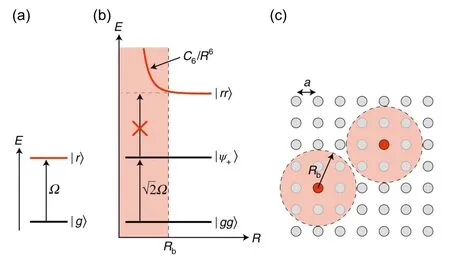
Fig.1. Schematic diagram of Rydberg blockade[12]. (a) The ground state|g〉is coupled to the excited state|r〉with Rabi frequency ?;(b)there is an energy shift of the doubly excited state due to van der Waals interaction,and collective Rabi frequency is enhanced to√; (c)atoms in Rydberg state(red dot)suppress excitation of atoms within their blockade volume.

2. One-dimensional Ising model

The spin system is one of the most investigated topics in the many-body regime. Interactions between Rydberg atoms are long-range,which well suits simulations of interactions in spin systems. Exploiting the ground state and Rydberg state to represent two types of spin states,[22,23]the Rydberg manybody system is able to realize simulations of the quantum Ising model.[24,25]

Ising model has been studied for about sixty years,which mainly contributes to quantum magnetism,[26]phase transition, and optimization problems.[27]Quantum simulations of Ising model have been realized in multiple many-body systems, such as ions,[2,28,29]superconducting,[30]and optical systems.[31]Rydberg many-body system becomes a hot topic only in recent decades owing to the development of some fundamental techniques. The development of laser-cooling,quantum gas microscope,[32,33]optical tweezers,[34–37]and magneto-optical traps[38,39]make it possible to control individual atoms precisely so that different distributions of particles in the system could be realized to satisfy research requirements. Thanks to advances in these techniques,several quantum simulations have been realized in the Rydberg many-body system,[12]such as both of one-dimensional[16,17]and twodimensional[40,41]Ising models. As shown in Figs. 2(a) and 2(c), a one-dimensional array is created by optical tweezers,while a two-dimensional array is prepared by a spatial light modulator (SLM). Moreover, Rydberg excitation is prepared through two-photon transitions that atoms in the ground state|g〉 are excited to the Rydberg state |r〉 via an intermediate state,as shown in Figs.2(b)and 2(d).

Quantum simulation of the one-dimensional Ising model is the simplest scenario and thus has been widely studied.The scale of simulation is up to tens of particles. A onedimensional 51-atom quantum simulator based on the Rydberg many-body system has been achieved.[17]Additionally, quantum simulators with two-dimensional arrays are reported,[16]which can realize circle one-dimensional simulators with periodic boundary conditions(PBC)to avoid edge effects in simulators with linear arrays.

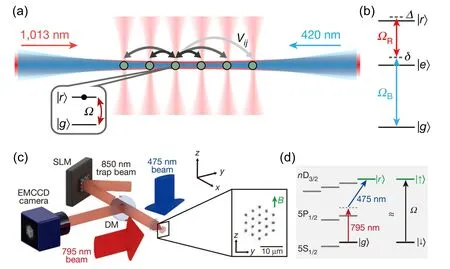
Fig.2. Experimental setups and energy levels of one-dimensional and two-dimensional Ising model: (a) a one-dimension array is prepared by optical tweezers and atoms are excited by 420 nm and 1013 nm pulses;[17] (b)energy levels for(a),the ground state|g〉=|5S1/2,F =2,mF =?2〉is coupled to|e〉=|6P3/2,F =3,mF =?3〉firstly and then to the Rydberg state|r〉=|70S1/2,J=1/2,mJ =?1/2〉, blue line corresponds to 420 nm pulse with Rabi frequency ?b,while red line corresponds to 1013 nm pulse with Rabi frequency ?R;[17](c)a two-dimension array is created by SLM and results are imaged on electron-multiplying charge-coupled device(EMCCD)camera through a dichroic mirror(DM);[16] (d)energy levels for(c),a 795 nm pulse couples the ground state|5S1/2〉to|5P1/2〉and then a 475 nm pulse couples|5P1/2〉to the Rydberg state|nD2/3〉.

Previous research mainly examines the ground state of many-body systems with different interactions and evolution processes. In order to realize different interaction strengths,one method is varying distances between atoms a in the array,while another is exploiting different Rydberg states to realize different blockade radius Rb. Mikhail D. Lukin group realized a 13-atom one-dimensional simulator and explored the evolvements of many-body systems for several different interaction strengths.[17]As shown in Fig.3(a), different interaction ranges Rb/a between 2 and 4 correspond to specific crystalline orders named Znorder for the interaction strength of n ?1 ＜Rb/a ＜n. There are always Rydberg excitations in both sides for all cases, but gaps between Rydberg excitations are proportional to Rb/a. The experimental results shown in Fig.3(b) are consistent with the theoretical prediction. Similar experiments conducted with two-dimensional arrays are reported by Labuhn et al. in 2016.[16]In that work,a circle-arranged 8-atom chain quantum simulator with periodic boundary conditions explores evolvement of the number of Rydberg excitation in the cases of Rb/a ＜1, Rb/a ≈1.5,and Rb/a ?1, respectively.[16]Due to excitation blockade,one excitation will suppress simultaneous excitation of a certain number of neighboring sites and limit the number of Rydberg excitation. Take Rb/a ≈1.5 for example, one excitation suppresses the most-neighboring excitation so that at most four nonadjacent sites can be excited simultaneously.Rydberg fraction fRis defined as the ratio of the average number of Rydberg excitation to the number of all particles in the system,showing that the number of Rydberg excitation oscillates with different peaks. As shown in Figs. 3(c) and 3(d), there are at most four excitations for Rb/a ≈1.5 while only one for Rb/a ?1,which are in great agreement with the expected results. In addition,the authors further verified these properties in larger systems. For larger systems with the atom number up to 20 when Rb/a=4.3,the system’s behaviors are still consistent with theoretical predictions.

Furthermore,Mikhail D.Lukin group explored the probabilities of occurrences of perfect many-body ground states.[17]If every particle in the system is interaction-free and randomly excited, the probabilities that the system is in the perfect ground state after a certain evolvement time decrease exponentially with the size of the system. Mikhail D. Lukin group found that the possibilities decrease linearly with the size in interacting Rydberg many-body systems, as shown in Fig.4(a). Additionally,they found that the Z2ordered ground state is the most frequently observed state after evolvement.As shown in Fig.4(b), the ground state is one of 251states,but it appears 20 times in 18437 experiments,much more than other states, indicating a quite strong quantum coherence of the many-body system during evolvement.

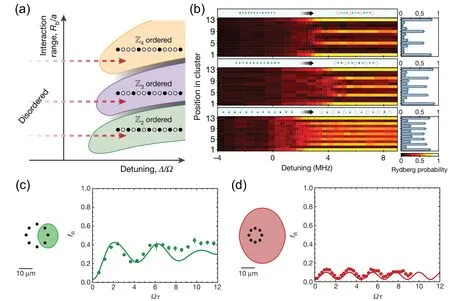
Fig.3. Experimental results in one-dimensional quantum simulators. (a) Scheme of Zn ordered evolvement;[17] (b) evolvements in the 13-atom simulator for Z2,Z3,Z4 ordered,respectively;[17] (c)Rydberg fraction after an excitation pulse of area ?τ in the circle-arranged 8-atom quantum simulator for Rb/a ≈1.5;[16] (d)Rydberg fraction in the circle-arranged 8-atom quantum simulator for Rb/a ?1.[16]

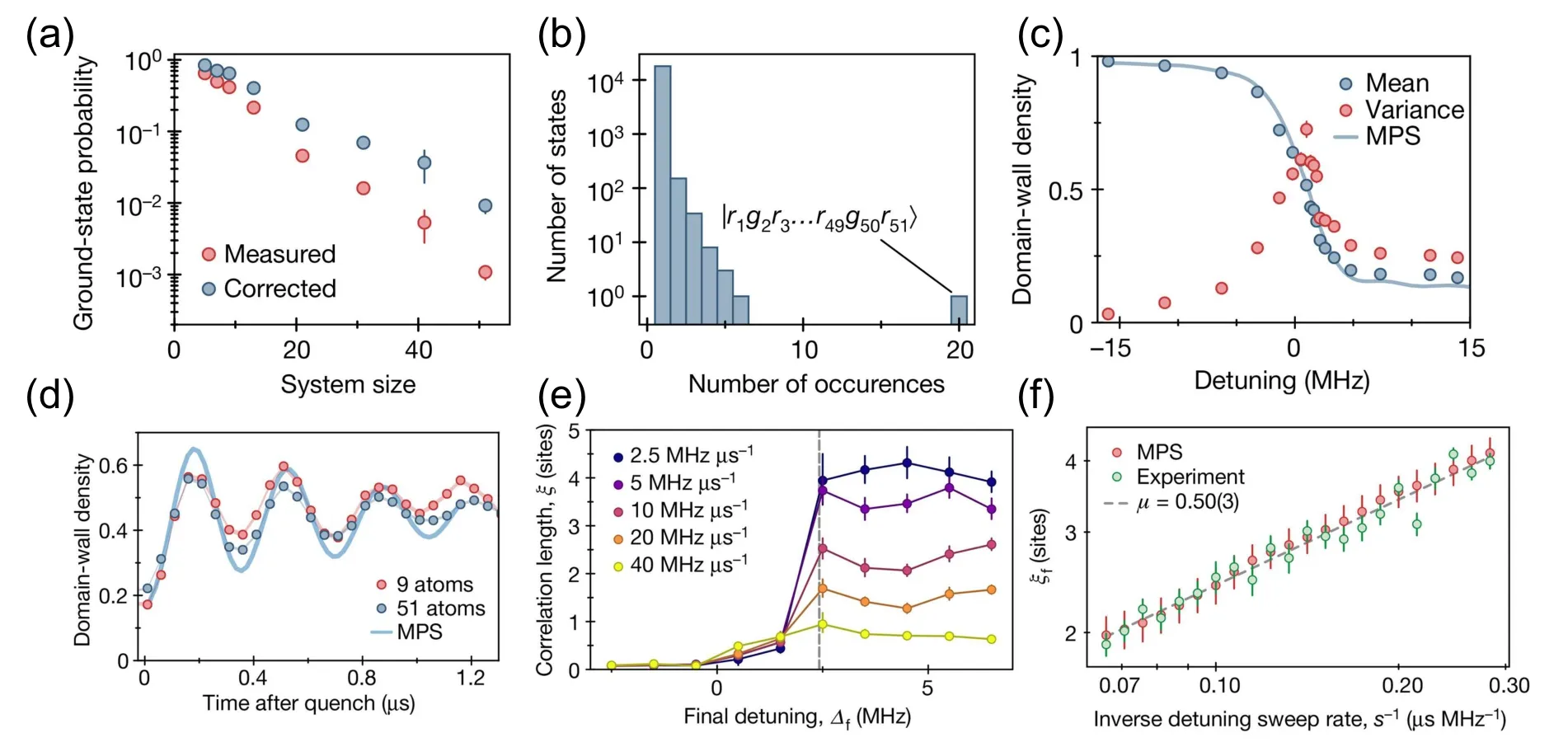
Fig.4. Further experimental results in one-dimensional simulators. (a) Ground-state probability as a function of system size;[17] (b) statistic of occurrence numbers for different states in 18439 times experiments;[17] (c)domain-wall density and variance of domain-wall density as a function of detuning;[17] (d)domain-wall density as a function of time after a quench;[17] (e)correlation length as a function of final detuning for different sweep speed;[18] (f)correlation length as a function of sweep rate.[18]

In order to characterize the transition from the disordered phase to the Z2ordered phase, a domain wall is introduced, which is defined as two neighboring atoms both in the same states,and thus the domain-wall density is defined as the domain wall number to all two neighboring atoms number ratio. From the disordered phase to the ordered phase,the domain-wall density decreases with a slow speed at the beginning but then sharply reduces, as shown in Fig.4(c). Finally,the domain-wall density is stable at a low level,indicating the built-up of the ordered phase of the system. There is an apparent peak for the variance of domain-wall density,which can be seen as a signature of the phase transition. Furthermore, the peak is lightly shifted to a positive value, in agreement with theoretical predictions.[42,43]

Further, the cases far from equilibrium are explored by Mikhail D. Lukin in Refs. [17,18]. The 51-atom many-body system is prepared in Z2ordered phase,and then the detuning is suddenly changed to zero. After such a quench,many-body states of the system oscillate between Z2ordered crystal state and the state where every atomic state reverses. Meanwhile,domain-wall density oscillates with a frequency irrelevant to the size of the system,as shown in Fig.4(d),where MPS(matrix product states) refers to results of numerical simulations exploiting MPS. Additionally, for the Z2ordered phase transition,a slow sweep results in fewer defects,namely,a larger correlation length. As shown in Fig.4(e),for a certain sweep rate,the correlation length suddenly saturates with final detuning increasing. However, different from the identical critical detuning value for all sweep rates,final correlation lengths increase with decreasing sweep rates. Further exploring the relation between final correlation lengths and sweep rates could be found in Fig.4(f). The final correlation lengths linearly increase with inverse detuning sweep rates on a logarithmic scale. This suggests the correlation lengths obey an exponential reduction with sweep rates increasing. These observations verify the quantum Kibble–Zurek mechanism[18]and provide experimental bases for non-equilibrium dynamics of quantum many-body systems.

3. Two-dimensional Ising model

Two-dimensional Ising model is also widely studied in the Rydberg many-body system.[16,40,41,44]A 7×7 square array simulator is reported to explore the behaviors and dynamics of two-dimensional many-body systems.[16,44]In order to describe correlations among atoms at different sites, twodimensional Rydberg–Rydberg correlation function g2(k,l)is defined. The observed correlation in Fig.5(a)shows antiferromagnetic characteristics of the many-body system in the central area. Additionally,an antiferromagnetic signature in a triangular array with 36 atoms was observed in Ref.[40]. However,only for appropriate final detuning within a certain range,the final states of the many-body system show obvious signatures of the antiferromagnetic phase, as shown in Fig.5(b),where the middle final detuning case shows the most obvious character of antiferromagnetism. Furthermore, for the same final detuning, a lower sweep leads to stronger correlations.But when the sweep speed is lower than a certain value, the correlations decrease due to the single-atom dephasing. As shown in Fig.5(c), the most apparent signature is the third case of an intermediate sweep speed compared to other cases.Lastly,the dynamics of the many-body system after a sudden quench is explored,[41]and the signatures of long-range antiferromagnetic correlations are observed. These observations and conclusions provide bases for further research of quantum simulations in higher dimensions and larger scales.

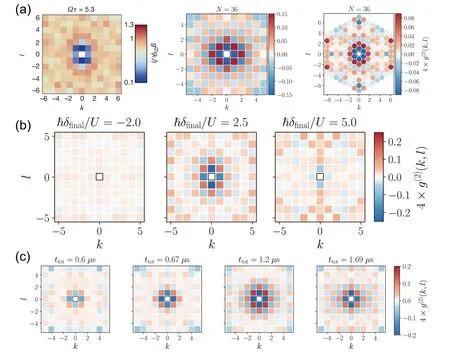
Fig.5. Experimental results in two-dimensional quantum simulators. (a) Correlation functions of final states, left for the 7×7 square array,[16]middle for the 6×6 square array and right for the triangular array with 36 atoms;[40] (b)correlation functions for different final detuning δfinal;[40](c)correlation functions for different detuning sweep rates.[40]

4. The XY model

While the Ising model exploits interactions between atoms in the same Rydberg states, XY model, namely the spin-exchange model,takes advantage of the resonant dipole–dipole interactions between atoms in different Rydberg excited states. As another common model of spin system, XY model is also used to explore transport properties besides quantum magnetism,which is widely demonstrated with Ising model.

Experiments exploring excitation transport are conducted in arrays with two and three atoms.C.S.Adams group demonstrated the ability to control the quantum state of Rydberg excitation exploiting microwave field,[45]providing an effective method to prepare two different Rydberg states in one manybody system. Two different Rydberg states are marked as|↓〉and|↑〉,respectively. For the two-atom case,Rydberg state is initially set as |↑↓〉, and states of both sites oscillate periodically. The frequency depends on the interaction energy,which can be varied by changing the distance between two atoms.And for the three-atom case, the initial state is set as |↑↓↓〉,and for ideal nearest-neighbor interactions, states of sites at both sides oscillate with an identical frequency but twice for the middle site. Additionally, as shown in the left picture of Fig.6(a),the population of|↓↑↓〉oscillates from 0 to 0.5,while the populations of|↑↓↓〉and|↓↓↑〉both oscillate from 0 to 1.Taking long-range interactions into consideration,as shown in the middle picture of Fig.6(a), periodic oscillations for the populations of|↑↓↓〉and|↓↓↑〉are destroyed.

Systems with more than three particles have been achieved in a different way.[34]And the energy transport is explored in the Rydberg many-body system.[46]A further direction may be towards large systems with up to tens of particles. Once achieved, these large systems will be ideal platforms for further research,such as quantum walks[47]and excitation hopping.[48]

5. SSH model

Another model exploiting interactions between atoms in different Rydberg states is the Su–Schrieffer–Heeger model (abbreviated to SSH model), which is initially built for studying soliton in polyacetylene.[49]Recently, in the quantum regime, symmetry-protected topological phases(SPT phases)[20,21,50,51]is an attractive research topic where the SSH model plays an essential role. Researches of symmetry-protected topological orders in the interacting bosonic system,[21]such as SSH model, and Fermi systems,such as the exotic topological density wave[50]and f-wave superfluidity[51]in Rydberg-dressed Fermi gas, provide advanced insights for many-body dynamics.

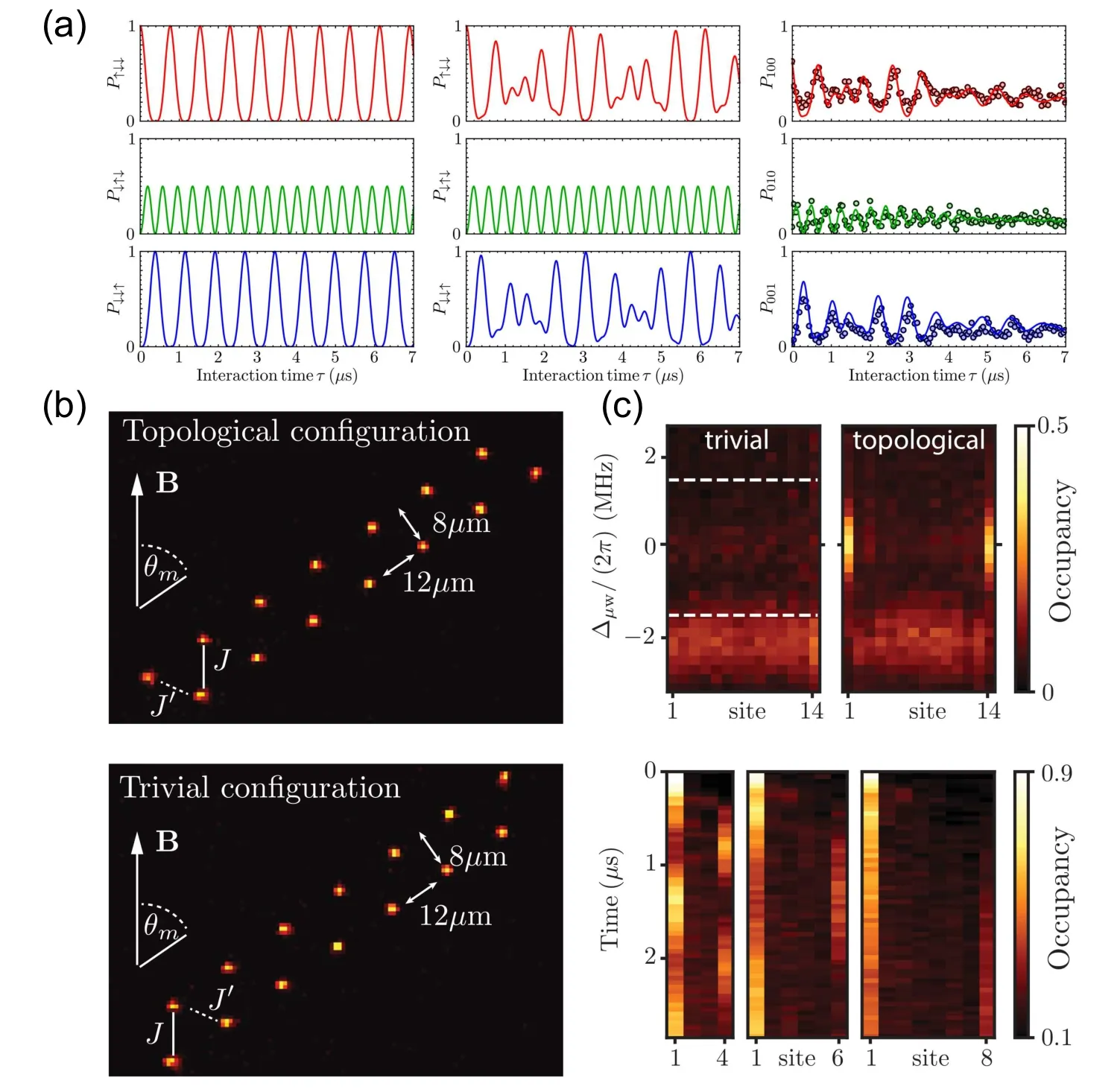
Fig.6. Results for XY model and SSH model. (a) Predicted results[19] (left for ideal nearest-neighbor interaction and middle for long-range interactions)and the experimental result(right)of an XY model system with three atoms;(b)arrays for the topological state(above)and trivial state(below)while J is an interaction stronger than J′;[21](c)spectrum of two phases for a system with 14 atoms(above)and particle transfer in systems with 4,6,8 sites(below).[21]

One-dimensional bosonic SSH model has been realized in Rydberg many-body systems, and challenging interacting cases have been explored.[21]Realization exploits the technology that a microwave field controls the Rydberg states of excited atoms. Firstly, as shown in Fig.6(b), two sub-chains of identical particle numbers are arranged in parallel, and all staggered atoms are excited to an identical Rydberg state.And then, a microwave field is provided to change the initial Rydberg states into another Rydberg states. Therefore,the system consists of two Rydberg states, and interactions between atoms are changed to resonant dipole–dipole interactions whose strength varies with angles. There are two interactions with different strengths,and two phases are formed.

The system is in the trivial phase when strong interactions exist at both edges while the topological phase corresponds to the case where weak interactions are at edges, as shown in Fig.6(b). For the trivial phase, the spectrum consists of two bands with an identical width. As shown in the upper panel of Fig.6(c),assisted dashed lines mark boundaries,but the upper band is not observed in experiments because of weak coupling from the initial state to these states. For the topological phase,shown in the upper panel of Fig.6(c),there is an obvious edge state around the zero energy,which is an essential signature of the topological phase. And further, particle transfer between two edges is discussed for chains with different lengths. One particle is prepared at the left site while the right site is empty.As seen in the lower panel of Fig.6(c), the occupancy of the right site is evident for the 4-site system but not for the 8-site system. Experimental results suggest that the hybridization of edge modes is obvious for small chains. Additionally,the system in the topological phase whose ground state is fourfold has a symmetry protecting mechanism; namely, small perturbations are not able to break the many-body ground state degeneracy. Higher dimensions and quantum topology are further directions in these many-body systems.

6. Non-equilibrium phase transition

Besides several common models with a small scale of particles and precise controlling of individual atoms,more quantum simulations of many-body systems are realized to uncover special behaviors and laws of many-body dynamics.

Electromagnetically reduced transparency(EIT)is a technique widely used for Rydberg state detection. Its nondestructive character and high sensitivity make it a powerful tool to explore many-body dynamics in Rydberg many-body systems.[52]EIT always occurs in the system with three energy levels,including a ground state,an excited Rydberg state,and an intermediate state. A weak probe beam couples the ground state to the intermediate state while a strong coupling beam couples the intermediate state to the Rydberg state. When the detuning of the coupling beam is close to zero, the transmission of the probe beam suddenly increases, which implies a greatly low abortion of the probe beam. This effect characterizes the properties of the Rydberg many-body system,contributing to the understanding of many-body dynamics.

In Rydberg ensembles, there are two phases. A low Rydberg excitation density corresponds to the no interaction phase (NI phase), while a high density refers to the interaction phase (I phase) where Rydberg excitations interact with large strengths so that the properties of the system vary. Optical bistability[53–57]is one of the interesting phenomena occurring in I phase,and is observed in multiple Rydberg manybody systems. And an additional field besides the probe and coupling field is able to control the critical condition from NI phase to I phase.[58]Additionally,many-body systems with a critical Rydberg density between NI phase and I phase become more sensitive to fluctuations.

The Rydberg excitation density NRdetermines the phase of the many-body system,while the probe beam,the coupling beam,and Rydberg states influence the Rydberg density. Ding et al. studied the evolvement of many-body systems depending on the parameters of the coupling detuning ?c, the probe Rabi frequency ?p, and the coupling Rabi frequency ?c,[58]while Melo et al. reported the influence of the principal quantum number[54],respectively. In order to obtain the transmission spectra, the coupling detuning is scanned from the negative detuning to the positive detuning and from the positive to the negative, respectively. As shown in Fig.7(a), with an increasing principal quantum number,the difference between two sweeping directions occurs, and the peak is shifted from zero to a negative value far from zero. And then,cases where?pvaries from low level to high level is discussed. For low?p,the transmission is irrelevant to the scanning direction of the coupling detuning and presents a symmetrical curve in the spectra. But in the case where ?pis high,in a negative interval and a positive interval, the transmission is different even for the same ?c, depending on the scanning direction. These phenomena are called optical bistability,simply understood as cases that two different responses are responsible for one input,whose occurrence is an essential signature of a transition from NI phase to I phase. When both ?cand ?pvary simultaneously and the transmission spectra are detected,as shown in Fig.7(b),a phase diagram is produced,which shows a clear distribution of phases and a clear critical boundary between two phases.

Further, the systematic dynamics at the critical point is discussed. Recently, Ref. [56] reported the influences of two factors on the transition threshold. One is changing the coupling Rabi frequency ?cfor a certain ?p. As shown in Fig.7(c), as ?cincreases, the overall transmission gets high.The transmission variance of ?calso increases with ?c, and diverges when ?cgets close to the threshold of the transition.Another is applying a switching field,which strengthens coupling from the ground state to the intermediate state without changing properties of the probe beam. Results are shown in Figs.7(d)and 7(e),suggesting that the threshold is lower with a switching field while the overall transmission phase diagram keeps a similar distribution compared to the case without a switching field. Exploiting this property, the transition of the Rydberg many-body system can be controlled simply by an additional field,which is greatly convenient for further explosion and application.

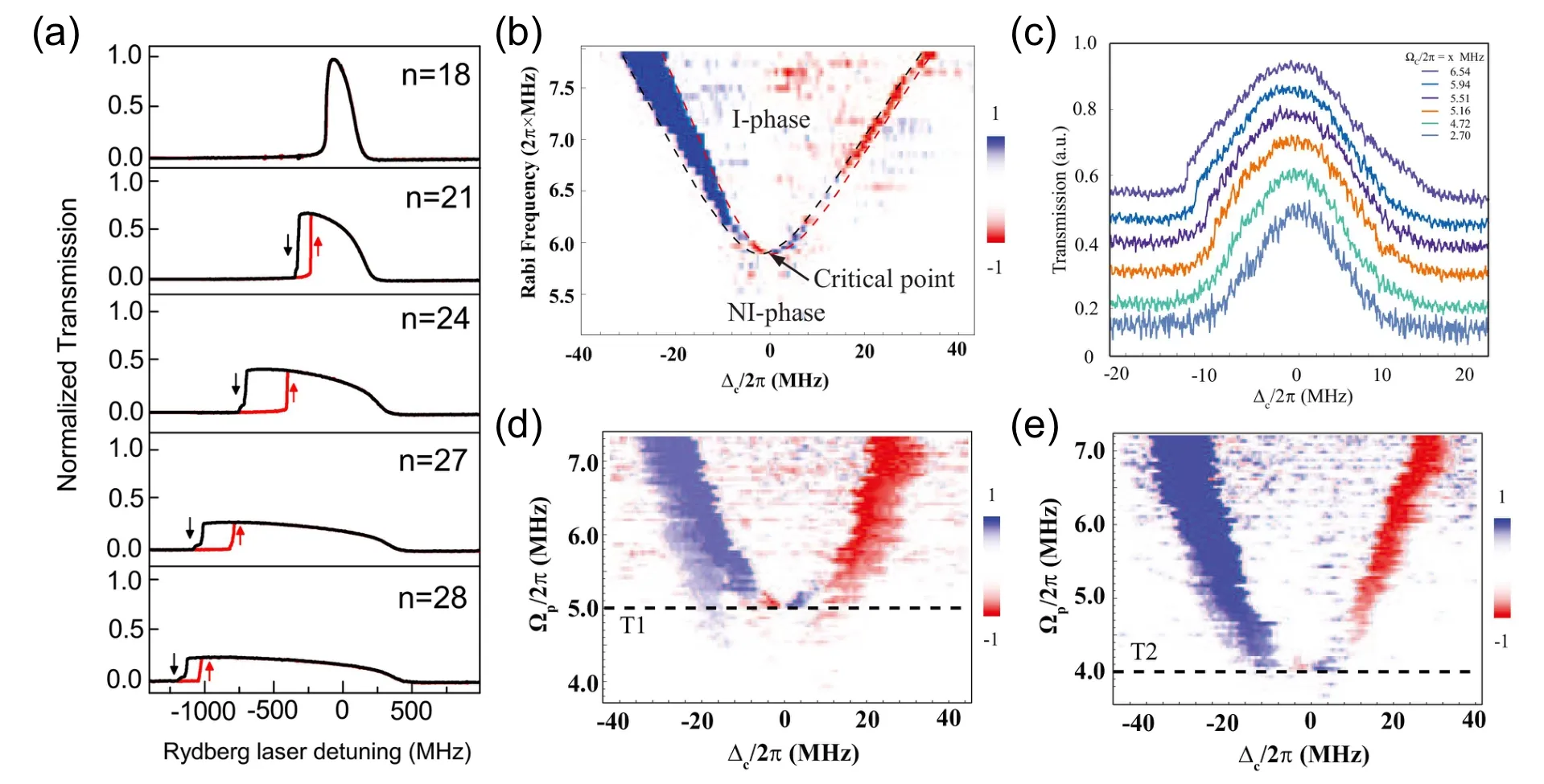
Fig.7. Bistability and phase diagram. (a) Normalized transmission as a function of detuning for the different principal quantum number;[54](b) phase diagram of ?p and ?c;[58] (c) transmission as a function of ?c for different ?c;[58] (d) phase diagram without a switching field;[58](e)phase diagram with a switching field.[58]

Self-organization is a common phenomenon in nature,widely existing in many-body systems of different fields besides physics, such as diseases[59]and forest fires.[60]Selforganized criticality (SOC) describes behaviors of manybody systems close to a transition independent of other nonequilibrium descriptions, and is able to partly explain complex structures in nature.[61]About thirty years ago,the forestfire model was built and developed to study self-organized critical behaviors.[62]And recently, this model has been mapped into the Rydberg many-body system to study critical dynamics.[58,63]Self-organization of the Rydberg many-body system is explored with the help of the forest-fire model.[58,62]A cell is randomly filled with Rydberg atoms and ground atoms with different numbers. The cell is in I phase if the number of Rydberg atoms is larger than the threshold of a phase transition,in NI phase for the opposite case or depleted of Rydberg excitation. Corresponding to the forest-fire model,cells in I phase are burning trees,and cells in NI phase are unburned trees, while depleted cells are empty grounds without trees. Then,iterating laws are needed to determine the following processes. NI phase cells near cells in I phase will be in I phase, and I phase cells become depleted cells. These correspond to cases that unburned trees are lightened by the neighboring burning tree,and burning trees burn out. Additionally,depleted cells are able to be NI phase cells with possibility p corresponding to the case that a new tree grows in an empty ground. And NI phase cells are able to be I phase cells with possibility f corresponding to the case that unburned trees are lightened by the light of burning trees far away. A simulation is conducted in a 100×100×100 array.[58]Results shown in Fig.8(a) suggest that large p leads to large I phase clusters.Further analysis discovers that the cumulative distribution of cluster sizes follows a power law, and the power-law exponents vary with f and p. However, the power-law exponent tends to an identical value,2,when f/p is close to the limit 0.Additionally,simulations explore the relation of the fire pixel fraction against the forest density. Results show that the fire pixel fraction keeps low close to 0 when the forest fraction varies from 0 to 0.3, and then suddenly increases to a high value over 0.8 for the interval from 0.3 to 0.4. Corresponding to the Rydberg many-body systems, this behavior suggests a critical threshold of Rydberg populations.

Three signatures of SOC are summarized by Whilock et al. through experimental results.[63]One is that the total atom density will decline to the same value once the initial density is larger than the threshold while the density almost remains constant for low initial densities. As shown in Fig.8(b), the final atom densities all tend to an identical value as soon as initial densities are over about 0.08 μm?3. Two different behaviors correspond to two phases of the many-body system,indicating a phase transition and SOC. To describe the second signature, the stationary state is defined as the final state where the system has the same density despite of the initial densities n0, and the final density is marked as nf. And the second signature is that variances of nfwith driving intensity are identical for all cases n0>nfand independent of initial densities. This behavior can be characterized by a decay curve obeying a power law, as shown in Fig.8(c). Lastly, the third signature is that large fluctuations exist even when the many-body system reaches the stationary state. As shown in Fig.8(d),Rydberg numbers fluctuate from zero to several hundred, showing avalanches triggered by the individual excitation. Further, the distribution of avalanche sizes is explored,which shows that occurrence possibilities decline exponentially with avalanche sizes. These properties provide a basic understanding of SOC in many-body systems and further mechanisms of non-equilibrium dynamics.

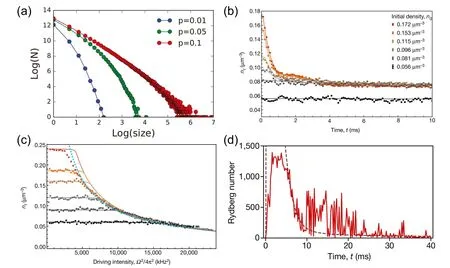
Fig.8. Self-organization in Rydberg many-body system. (a)Distribution of clusters in different sizes;[58] (b)atom density as a function of time for different initial densities;[63](c)final atom density as a function of driving intensity for different initial densities;[63](d)Rydberg number oscillation in the stationary state.[63]

7. Conclusion and perspective

In the real world, many-body systems with interactions are more common than isolated systems. While calculations are far over the classical computation limit, quantum simulation is one of the most effective methods to deal with many-body problems until the realization of quantum computation. Because of strong interactions and easy manipulations, the Rydberg many-body system is an ideal platform for quantum simulations. Several models have been realized in the Rydberg many-body system, such as the Ising model for quantum magnetism and the forest-fire model for selforganized criticality. These simulations successfully reproduce some behaviors in real-world many-body systems and provide insights into many-body dynamics,especially for nonequilibrium processes, which are much common in nature.Additionally, Rydberg many-body systems contribute to further research of problems in the quantum regime,such as optimization problems[64,65]and the self-verifying quantum variational simulation.[66]

Despite many successful cases, in the future, Rydberg many-body systems need to increase scale to achieve simulations in large systems,and the maintaining time of the system needs to extend to allow the system evolves fully so that more many-body behaviors can be observed.And more types of particles in Rydberg systems need to develop for better or novel properties.[67,68]Additionally,the Rydberg many-body system is a promising platform[69]to achieve the quantum computer,which is one of the most expected achievements in the future.